Categorie: Relatività
Tags: distanza relativistica distanza spaziotemporale invariante relativistico Minkowski paradosso dei gemelli quiz relatività speciale
Scritto da: Vincenzo Zappalà
Commenti:4
QUIZ sul minimo percorso relativistico ***
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento
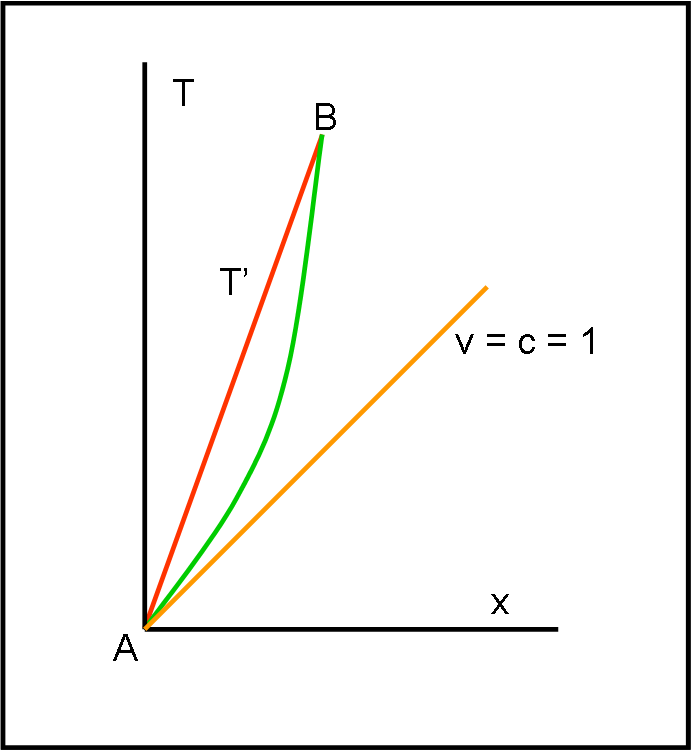
La domanda è estremamente semplice e si riferisce alla Fig. 1. Siamo nel diagramma di Minkowski e AB è un intervallo spaziotemporale. Ricordo che questo intervallo è un invariante relativistico e rimane costante per ogni sistema di riferimento. Lo conosciamo molto bene e l’abbiamo già usato per descrivere le curve di calibrazione. La formula che lo esprime è:
s2 = T’2 = T2 – x2
Vi chiedo: “Qual è la distanza relativistica MINORE tra l’evento A e l’evento B? L’intervallo rettilineo rosso o quello curvilineo verde?”.
Ovviamente non mi basta la risposta (50% di probabilità), ma dovete dimostrare geometricamente il risultato che avete “scelto”e, poi, utilizzarlo per dimostrare immediatamente il paradosso dei gemelli. Mi attendo che facciate anche il viceversa: partendo dal risultato relativo al paradosso dei gemelli, trovare immediatamente la soluzione del quiz.
Buon divertimento!
P.S.: la soluzione esatta e generale si ottiene attraverso l’operazione di integrale. Ma io non VOGLIO questi slanci… eruditi. Si può ottenere lo stesso risultato (altrettanto valido) senza alcun integrale e mettendosi in un caso particolare, ma più che significativo.
LA SOLUZIONE E' NEI COMMENTI
4 commenti
Enzo , se puoi dovresti bloccare le risposte per una settimana; così, secondo me diventa più divertente
Dopo una settimana senza PC (mi è toccato portarlo a riparare
), provo a rispondere al quiz.....noto con dispiacere che nonostante il fermo obbligato sono comunque il primo che prova a rispondere 
, per cui se qualcuno si sta cimentando nella soluzione il consiglio è quello di leggere questo post dopo averci provato (giusto per non confondersi le idee, dato che la soluzione proposta potrebbe non essere quella giusta).
Prima di proporre la figura che ho realizzato, vorrei fare alcune brevi premesse.
Il diagramma rappresenta tre diversi sistemi:
1) quello “fermo” rappresentato dagli assi T e x;
2) quello in movimento a velocità 0,35C (linea rossa) che dal suo punto di vista si sposta solo nel tempo, ossia lungo il suo asse T' (x'=0). Infatti solo per altri sistemi esterni questo sistema si muove anche nello spazio;
3) quello in movimento lungo la linea verde.
Quest'ultimo sistema è diverso dagli altri due, poiché la sua velocità non è costante (ossia varia nel tempo e nello specifico ad un certo punto, in prossimità di C, decelera).
Dato che la curva ha due lunghi tratti che sono riducibili ad una retta (velocità costante), ho approssimato tale percorso spazio-temporale, come se si trattasse di due velocità, una che contraddistingue la prima parte del percorso (A-C) stimabile in 0,71C e l'altra che contraddistingue la seconda parte del percorso stimabile in 0,15C.
Quindi l'asse del tempo T'' , visto da sistemi esterni, in prossimità dell'evento C cambia, per cui varia l'inclinazione della retta che lo rappresenta e variano anche le rispettive linee di simultaneità (una per il tratto A-C e l'altra per il tratto C-B).
Nella figura ogni sistema (assi del tempo: T, T' e T'') ha le sue unità di misura che rappresentano il tempo segnato dal proprio orologio fisso, mentre le linee di simultaneità rappresentano il tempo segnato da tutti gli orologi del sistema di riferimento posizionati su tale linea (linee nere, rosse o blu come i relativi assi del tempo).
http://www.astrobin.com/full/187783/L/
Per un ipotetico osservatore che viaggia lungo l'asse T'' (X''=0), l'orologio fisso rimane sempre lo stesso, ossia non cambia certo in prossimità di C , è visto da sistemi di riferimento esterni che la sua rappresentazione cambia profondamente.
Nello specifico: nel tratto A-C, l'asse T'' adotta l'unità di misura relativa a v =0,71C, mentre nel tratto C-B adotta l'unità di misura relativa a v=0,15C e di conseguenza cambiano anche le due rispettive linee di simultaneità.
Quindi per percorrere l'intero percorso impiega un certo tempo, dato dalla somma dell'intervallo di tempo A-C (misurato con la sua specifica unita di misura) e l'intervallo di tempo C-B (misurato con la sua specifica unita di misura).
Quindi, l'orologio del sistema T'' quando arriva in B segnerà un tempo:
T’’B =ΔT’’A-C + ΔT’’C-B = 1,26 + 2,87 = 4,13
I valori 1,26 e 2,87 sono stati ricavati usando le unità di misura adottate dall'asse T'' nei due tratti A-C e C-B.
A questo punto basta confrontare il tempo segnato dall'orologio fisso di T'' (T''B=4,13) con quello segnato dall'orologio fisso di T' (T'B = 4,41), per rendersi conto che la linea verde (approssimata a due rette blu) “percorre” la distanza spazio temporale A-B in un tempo più breve.
A questo punto non resta che confrontare cosa vede ogni sistema di riferimento.
Per il sistema fermo (nero) quando l'unico orologio fisso del sistema in movimento (rosso) T' segna 4,41, i suoi orologi (linea simultaneità nera) segnano T=4,7, per cui segnano un tempo maggiore di T', ossia il tempo sembra dilatarsi.
Per il sistema in movimento (rosso) quando l'unico orologio fisso del sistema fermo T segna 4,1 i suoi orologi (linea simultaneità rossa) segnano T=4,41, per cui segnano un tempo maggiore di T, ossia anche per il sistema in movimento il tempo dell'altro sistema sembra dilatarsi.
Una perfetta simmetria per cui ad entrambi i sistemi sembra che sia il tempo altrui a dilatarsi.
Una simmetria destinata a rompersi osservando il sistema T''.
Per il sistema fermo (nero) quando l'unico orologio fisso del sistema in movimento (blu) T'' segna 4,13 (arrivo in B), i suoi orologi (linea simultaneità nera) segnano T=4,7, per cui segnano un tempo maggiore di T'', ossia il tempo sembra dilatarsi.
Per il sistema in movimento (blu) quando l'unico orologio fisso del sistema fermo T segna 4,4 i suoi orologi (linea simultaneità blu) segnano T''=4,13, per cui segnano un tempo minore di T.
Sia per il sistema fermo sia per il sistema in movimento il tempo T'' 4,13 è sempre inferiore a T e la simmetria valida prima per sistemi che si muovono a velocità costante, si è rotta.
La situazione è ancora più chiara confronto il sistema in movimento rosso T' con quello blu T''.
Entrambi partono da A inseme ed arrivano in B, solo che chi viaggia nel sistema blu invecchia meno, dato che quando arriva in B il suo orologio fisso (tempo proprio T''=4,13) segna un tempo minore dell'orologio fisso di T' (tempo proprio T'=4,41).
La rottura della simmetria dovuta alla velocità non costante di T'', sembra rispondere al paradosso dei gemelli (in questo caso uno dei due invecchia davvero meno dell'altro).
In ultimo, una piccola considerazione sull'approssimazione della curva verde.
Guardando la figura in prossimità di C ho tracciato due diverse linee di simultaneità blu, una si riferisce alla prima parte del percorso e l'altra alla seconda parte.
Una parte della curva verde non coincide con le due rette ed in questo tratto la velocità cambia da V=0,71C a V=0,15C (decelerazione), per cui l'inclinazione della retta di simultaneità cambia da quella che congiunge C all'asse T=0,9 a quella che congiunge C all'asse T=1,6.
In pratica ho approssimato questo tratto, ottenendo un ipotetico “evento” C di intersezione tra le due rette.
In questo modo tale evento C subisce istantaneamente un salto temporale (misurato dal sistema fermo sull'asse T, da 0,9 a 1,6, ma lo stesso discorso si potrebbe fare misurandolo sull'asse T' del sistema rosso), che in realtà avviene più lentamente in un certo intervallo di tempo, dato che la curva verde (a differenza delle rette blu) indica un passaggio graduale da V=0,71 C a V =0,15C.
Paolo
La distanza relativistica MINORE tra l’evento A e l’evento B è quella curvilinea di colore verde.
vista l'indipendenza della distanza relativistica, possiamo supporre di metterci nel sistema di riferimento
in qui la velocità con cui viene percorso il segmento AB è zero. Ciò equivale a compiere una rotazione nel diagramma di Minkowski per cui il segmento AB viene a coincidere con un segmento sull'asse dei tempi di coordinate A(0,0) , B (0,T')
la curva verde subirà anch'essa una rotazione in modo che i suoi estremi coincidano con A,B.
Nei diagrammi di Minkowski il segmento di retta rappresenta la distanza massima rispetto alle spezzate che uniscono due estremi;(vale la disuguaglianza triangolare al contrario) ciò si può capire nel nostro esempio dal fatto che essendo nulla la componente spaziale la lunghezza del segmento AB è semplicemente T', mentre se dobbiamo calcolare la lunghezza della spezzata (una sommatoria degli intervalli) avremmo a che fare con termini sia temporali che spaziali; nella formula della distanza relativistica, a causa del segno meno che sottrae dalla parte temporale
al quadrato la parte a spaziale al quadrato avremmo perciò una somma totale minore di T' (le parti temporali si ottengono proiettando i vertici della spezzata sull'asse dei tempi)
potremmo estendere a spezzate sempre con più lati fino al limite per ottenere la curva.
Se questo è vero si risolve subito il paradosso dei gemelli, in quanto la spezzata del gemello in moto che inverte la rotta diventa un caso particolare di questo problema.
cari amici,
anche se siete solo due devo dire che avete azzeccato il problemino. Umberto è stato molto sintetico ed esauriente, mentre Paolo, come sempre, ha descritto completamente la situazione senza approfittare di generalizzazioni che renderebbero il tutto più semplice e immediato. La soluzione la darò all'interno del prossimo articolo (l'ultimo della seconda parte della RR). Questo articolo sarà una "bella" lettura per le ferie...