Categorie: Relatività
Tags: dilatazione dei tempi invarianti orologio a luce tempo proprio trasformazione di Lorentz
Scritto da: Vincenzo Zappalà
Commenti:10
La relatività speciale disegnata da Minkowski. 12: un orologio molto preciso ***
Tutto ciò che abbiamo ricavato finora sulla dilatazione dei tempi e sulla contrazione delle lunghezze, può essere dimostrato in modo molto più diretto e intuitivo, attraverso pochi e semplici grafici. Perché, allora, costringervi a trafficare con equazioni e con formule più o meno complicate e monotone? Presto detto. Innanzitutto, perché solo così si capiscono molto bene le ipotesi di partenza di Einstein; inoltre, si deve comprendere che esiste una trasformazione di coordinate, che coinvolge anche il tempo, in grado di sostituirsi a quella di Galileo e Newton. Essa rappresenta la realtà globale, di cui quella galileiana è solo una prima approssimazione, validissima per le velocità con cui l’uomo si scontra tutti i giorni. Guardando, però, le stelle e le particelle che vengono scaraventate verso di noi, non si può più fare a meno di una legge che le inglobi nello stessa visione d’assieme. Solo con questa nuova trasformazione sarà “facile” disegnare compiutamente lo spaziotempo.
Introduciamo, allora, un orologio molto semplice il cui tic-tac è veramente rapidissimo. Lo chiamiamo orologio a luce.
Per costruirlo abbiamo solo bisogno di due specchi piani e di una lampadina che invii un impulso luminoso in un certo istante. Dopo possiamo tranquillamente spegnerla. I due specchi sono sistemati uno di fronte all’altro “in verticale”, in modo che il movimento della luce avvenga lungo un certo asse y. La lampadina che invia la luce è posta al centro dello specchio A. A noi interessa solo ciò che fa la luce emessa a un certo istante t. Essa si dirige verso lo specchio B e poi torna indietro, riflettendosi, per colpire di nuovo lo specchio A. Nuova riflessione e via dicendo. Un’operazione semplicissima che conosciamo molto bene anche attraverso la QED. La distanza tra i due specchi sia, ad esempio, L0 = 1 m. La luce viaggia a circa 300 000 km/sec, il che vuol dire che per andare da A a B e tornare in A il tempo è stato solo di 6.6 10-9 sec. Questo può essere considerato il tic-tac dell’orologio. Il tic è da A a B e il tac da B ad A. Avevo o non avevo ragione a dirvi che il tic-tac era rapidissimo? La Fig. 1 illustra l’orologio a luce.
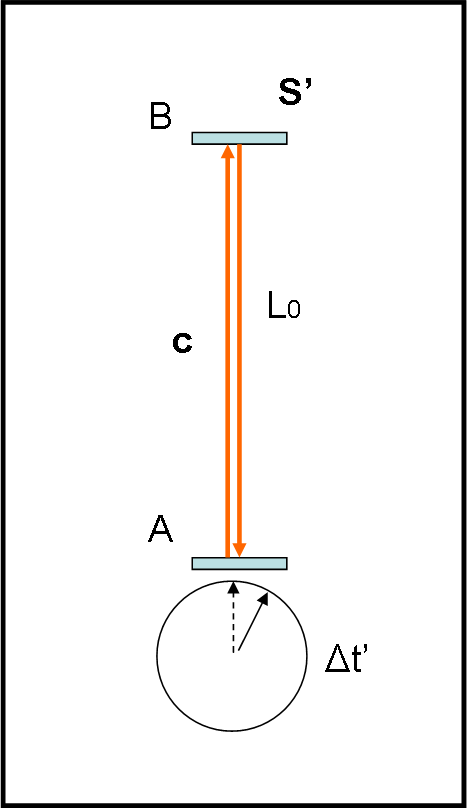
Tutto queste banali operazioni le abbiamo fatte su un sistema di riferimento S’. Il nostro orologio è solidale con questo sistema e i tempi di partenza e di arrivo della luce sono misurati, ovviamente, con lo stesso orologio. I due specchi e l’impulso di luce sono, infatti, veramente un orologio, in quanto basterebbe inserire un contatore in A che segnali ogni arrivo della luce e che, quindi, scandisca il tempo ogni 6.6 10-9 secondi (o quello che scegliamo, cambiando la distanza L0). O, se preferite, che ad ogni arrivo della luce in A faccia girare di una certa quantità costante una lancetta.
Il tempo tra l’invio della luce e il suo ritorno in A è quindi un tempo proprio, ossia misurato in un sistema di riferimento con un solo orologio. Possiamo facilmente scrivere una formula che lo rappresenti e che si basi su due grandezze costanti per definizione: la distanza tra i due specchi L0 e la velocità della luce c. Il tempo necessario per andare da A a B non è altri che la lunghezza L0 divisa per la velocità c (la velocità costante non è altro che lo spazio diviso per il tempo), ossia:
t’B – t’A = L0/c
t1’A – tB = L0/c
Dove t1’A è l’istante di ritorno in A, mentre t’B è sia il momento di arrivo della luce in B che il momento della sua riflessione (è lo stesso identico evento). Indichiamo t’1A– tA come Δt’ (dato che si riferisce al sistema S’ e indica il battito costante dell’orologio). Possiamo quindi scrivere che:
Δt’ = 2L0/c …. (1)
Un orologio fantastico, estremamente preciso, almeno per chi vive su S’…
Vediamo, adesso, cosa succede se il sistema S’, e con lui l’orologio, è in moto con una certa velocità v rispetto a un sistema S. Scendiamo da S’ e guardiamo l’orologio dal sistema “fermo” S.
La figura da considerare è, adesso, la Fig. 2. Il movimento di S’ rispetto a S avviene lungo l’asse x, come al solito. La luce parta da A, ma, mentre viaggia verso l’alto, gli specchi si muovono solidalmente con il sistema S’. Quando la luce partita da A raggiunge B, questo si è spostato rispetto alla posizione che aveva al momento della partenza dell’impulso di luce. Esso si trova in B1 corrispondente al punto A1. La luce torna indietro, ma il movimento continua e ritorna in A quando questo specchio si è ormai portato in A2.
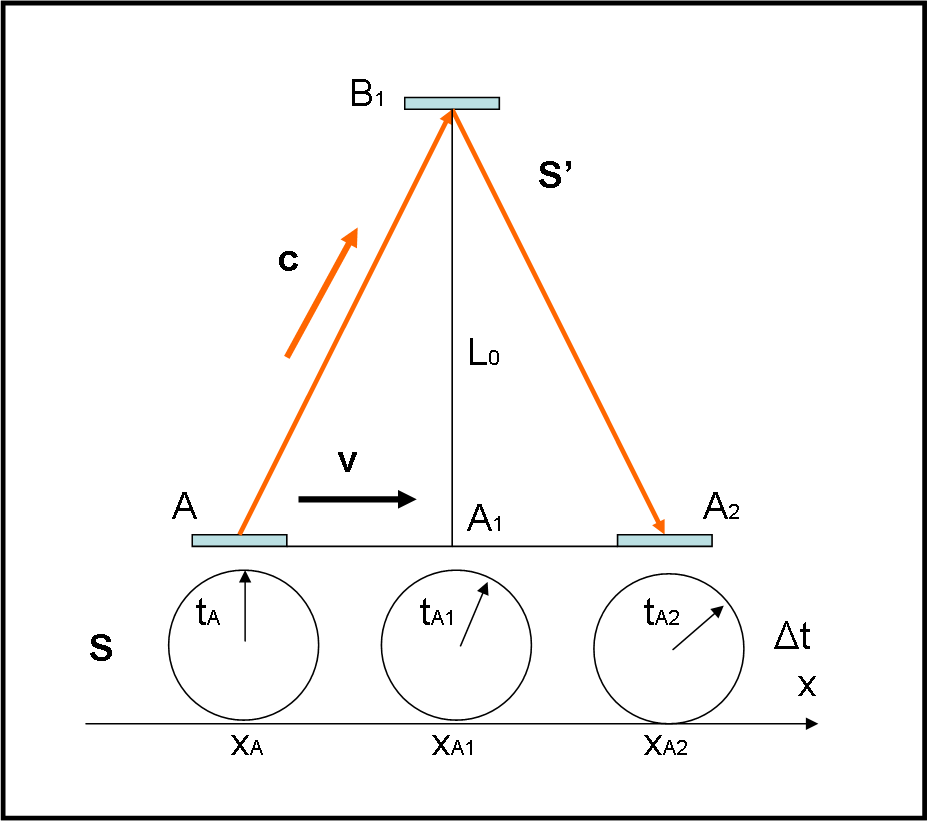
Fermiamoci un attimo per dimostrare esattamente la plausibilità di questa serie di eventi. Qualcuno potrebbe dire: “Perché mai devo considerare un raggio luminoso che viaggia da A a B1? La luce viaggia in verso verticale e non obliquo…”. Questa è una domanda che molti si fanno, ma che spesso “non si osa” esporre… E, invece è una domanda molto istruttiva perché ci riporta al postulato che dice che ogni fenomeno fisico deve essere identico se osservato in sistemi in moto uniforme tra loro. Non è molto diverso dall’uomo che versa l’acqua in un bicchiere a terra o su una nave, nella relatività galileiana.
Un “osservatore” nel nuovo riferimento deve sempre vedere il fascio di luce che parte dallo specchio inferiore, batte su quello superiore e torna di nuovo nello specchio inferiore (la coincidenza del fascio con i vari specchi, nei vari istanti, è un fatto fisico e deve essere uguale per tutti gli osservatori). In poche parole, la luce deve andare da A a B1 e poi da B1 ad A2.
Assodato questo fatto, consideriamo un'altra conseguenza della trasformazione di Lorentz. La distanza L0 è diretta lungo l’asse y e sappiamo benissimo che non vi è alcuna contrazione o dilatazione lungo le direzioni perpendicolari all’asse del moto x. Si può quindi essere sicuri che L0 mantiene la stessa lunghezza sia in S che in S’. Anche questa considerazione viene spesso tralasciata, ma è fondamentale per comprendere appieno il significato della relatività einsteniana.
Infine, non dimentichiamo che c deve essere la stessa in ogni sistema di riferimento.
Possiamo, finalmente, descrivere cosa avviene se l’orologio di luce viene visto da S.
Tutto si riassume benissimo nella Fig.2. La luce descrive il percorso A B1 A2. S non può che concludere, qualitativamente, che il percorso della luce deve essere più lungo di quello misurato nel sistema S’. Tuttavia, la luce ha sempre la stessa velocità c, e, quindi, se il percorso è più lungo deve essere più lungo anche il tempo impiegato a percorrerlo, dato che la velocità è pur sempre uno spazio diviso un tempo.
Passiamo, ora, a una descrizione quantitativa. Il percorso dello specchio A, mentre va da A a A1, è dato da (per semplicità, consideriamo sempre il centro dello specchio):
AA1 = xA1 –xA = v (tA1 – tA)
La distanza AB1 è data dalla differenza di tempo tA1 – tA (tA1 è uguale a tB1) moltiplicata per la velocità della luce c, ossia
AB1 = c (tA1 – tA)
Non ci resta che applicare il teorema di Pitagora al triangolo AB1A1.
AB12 = AA12 + A1B12
Ossia:
c2 (tA1 – tA)2 = (xA1 –xA)2 + L02
e anche:
c2 (tA1 – tA)2 = v2 (tA1 – tA)2 + L02
Per semplicità chiamiamo Δt1 la differenza di tempo tra la partenza della luce da A al suo arrivo in B1 (che corrisponde al punto A1), ossia tA1 – tA. La formula precedente diventa:
c2 Δt12 = v2 Δt12 + L02
Ricaviamo Δt1 …
Δt12(c2 – v2) = L02
Δt12= L02/(c2 – v2) = L02/(c2 (1– v2/c2)) = (L02/c2)(1/(1– v2/c2))
Non abbiamo fatto altro che usare un piccolo trucchetto, mettendo in evidenza c2 al denominatore… in modo che venisse fuori la quantità 1/(1– v2/c2) che ormai conosciamo molto bene!
Non ci resta, ora, che eseguire la radice quadrata e si ottiene:
Δt1 = (L0/c)(1/(1– v2/c2)1/2)
Tuttavia, lo stesso procedimento lo possiamo utilizzare per trovare la differenza di tempo Δt2 necessario per andare da A1 ad A2, ossia fino al ritorno del fascio di luce nello specchio di partenza A. Risulta immediato che Δt1 = Δt2. Ne segue che il tempo complessivo Δt perché la luce parta da A arrivi in B1 e torni in A2 non è altro che:
Δt = Δt1 + Δt2 = 2 Δt1 = (2L0/c)(1/(1– v2/c2)1/2)
Tuttavia, dobbiamo ricordare dalla (1) che:
Δt’ = 2L0/c
Sostituendo, otteniamo, infine:
Δt = Δt’/(1– v2/c2)1/2 …. (2)
Che non è altro che la trasformazione di Lorentz relativa al tempo.
Non dimentichiamoci mai che abbiamo ottenuto questo risultato, così discordante tra i due sistemi di riferimento, per il solito “vecchio” dato di fatto che abbiamo evidenziato fin dall’inizio, descrivendo la relatività della simultaneità: nel sistema S’ abbiamo utilizzato un solo orologio situato sempre nello stesso punto; nel sistema S abbiamo dovuto misurare il tempo attraverso orologi diversi, uno posto nella posizione A e uno in A2 (volendo, anche uno intermedio in A1). Il primo tempo è per definizione un tempo proprio, mentre il secondo è un tempo improprio.
Ribadiamo ancora che ∆t non ha, perciò, nulla a che vedere con il tempo segnato dall’orologio a luce che è sempre dato dal tempo proprio ∆t’, qualsiasi sia il sistema di riferimento. Non commettiamo l’errore di pensare che un orologio a luce si comporti in modo diverso cambiando il sistema di riferimento! E’ la stessa cosa che si otteneva con l’uomo sulla nave. L’azione di versare acqua in un bicchiere non cambia tra chi sta a terra o sta in nave. Il principio di relatività vale sempre. Nella relatività ristretta (e quindi nella trasformazione di Lorentz) ciò che cambia è la misura effettuata da un sistema in moto relativo rispetto a un altro.
N.B. Questa conclusione continua a essere valida anche se l’orologio a luce viene ruotato di 90° in modo che gli specchi siano allineati lungo l’asse x e, più in generale, per qualunque altro tipo di orologio (a pendolo, a quarzo, atomico, ecc...). Tuttavia, quando si dice “qualsiasi orologio” si intende proprio qualsiasi! Ad esempio, anche un orologio “biologico”, come il battito del cuore o il processo di invecchiamento. Esso non deve cambiare se l’essere vivente in questione si trova a terra o su una nave o su un razzo che viaggia a velocità costante, altrimenti vorrebbe dire che le leggi fisiche che sono alla base del funzionamento del cuore sarebbero diverse nei due riferimenti in aperto contrasto con il Principio di Relatività. Qualsiasi riferimento al paradosso dei gemelli NON è casuale…
Bene… attraverso il semplice teorema di Pitagora abbiamo ricavato nuovamente la trasformazione di Lorentz relativa al tempo, ossia la sua dilatazione. Con un procedimento analogo troveremo anche la contrazione delle lunghezze.
Appendice preveggente
Prima di proseguire in questa direzione, fatemi scrivere una relazione che deriva dal solito triangolo rettangolo che abbiamo usato precedentemente e che ci ha portato a:
c2 (tA1 – tA)2 = (xA1 –xA)2 + L02
Tuttavia, sappiamo che:
Δt’ = 2L0/c
Ossia:
L0 = c Δt’/2
Ponendo Δx = xA2 – xA = 2(xA1 –xA)
c2 Δt2/4 = Δx2/4 + c2 Δt’2/4
Ossia:
c2 Δt’2 = c2Δt2 - Δx2
Il primo membro è il quadrato del tempo proprio (qualsiasi sia il sistema di riferimento) moltiplicato per la velocità della luce al quadrato, il secondo membro è un qualcosa di “strano” che fa ricordare il teorema di Pitagora, ma con un segno invertito… Notiamo, però, che ogni fattore rappresenta uno spazio (il tempo per una velocità è uguale a uno spazio). Bene, non voglio anticipare molto di più, dato che ci torneremo sopra per affrontare in pieno il diagramma di Minkowski, mi basta dire che c2 Δt’2 è un invariante dello spaziotempo.
In poche parole, qualsiasi sia il sistema di riferimento S in moto rispetto a S’, la quantità precedente non cambia! Essa è una distanza invariante dello spaziotempo, così come la distanza tra due punti è un’invariante nello spazio euclideo. Senza nemmeno accorgercene abbiamo “toccato” lo spazio di Minkowski, capace di rappresentare la relatività ristretta con quattro coordinate (due se consideriamo lo spazio solo come x). Uno spazio quasi-euclideo, ma non euclideo, dato che vedremo che un’ipotenusa di un triangolo è più corta di un cateto… Tuttavia, come già detto, affronteremo nuovamente e con maggiore attenzione questo importantissimo argomento.






10 commenti
Vai Enzone, anche se sono costretto a seguirti .. a distanza, diciamo con tre o quattro articoli di ritardo.
Che vuoi fare, mai che ti pagassero per occuparti di cose veramente serie ed importanti!
P.S.: fortuna che nel blog appaio sotto falso nome!
Ciao Vincenzo, sono sempre il nuovo (vecchio...) Francesco :-)
Su questo orologio ho un dubbio che vorrei qualcuno più dotato di me mi chiarisse: Sono ragionevolmente certo che tutto sia a posto finché il moto resta costante. Intendo dire che il CONTEGGIO dei tic tac resta uguale per i due osservatori ma l'INTERVALLO di tempo tra ogni singolo tic tac risulta differente. Ora il dubbio: nel caso dei gemelli, quando uno dei due ritorna, è corretto affermare -come credo- che è proprio il CONTEGGIO dei tic tac a non essere più lo stesso e il viaggiatore col biglietto di ritorno ne ha contati meno del gemello pigro?
Ultimamente discutevo di un problema analogo ma relativo alla dilatazione temporale dovuta a campi gravitazionali: io sostenevo (ma non tutti erano d'accordo) che se tu resti a terra e io faccio un viaggetto lontano da campi gravitazionali (diciamo pure a con v<<c per evitare problemi con la RR), al mio ritorno io sarei più vecchio di te, proprio nel senso che il CONTEGGIO dei miei tic tac è maggiore del tuo. Io credo che sia corretto, ma mi resta la famosa pulce...
Per concludere, ha senso affermare che il TEMPO in fisica è proprio il CONTEGGIO dei tic tac di un orologio?
Grazie
Francesco
Esattamente Francesco
In realtà, nella RR non è chi viaggia che misura un tic tac più rallentato sul suo orologio, ma è chi vede l'orologio di quello che viaggia. Solo per lui l'orologio rallenta (stiamo attenti a questo punto essenziale: io, nel mio sistema di riferimento, sono fermo e osservo che l'orologio di chi viaggia rallenta. Ovviamente, vale anche il viceversa, dato che per chi viaggia, sono io che mi muovo e lui sta fermo).
Nel paradosso dei gemelli non vale più la RR, dato che a metà percorso vi è un cambiamento di sistema solo per chi viaggia e non per chi sta sulla Terra. Comunque, il paradosso, è stato trattato in decine di modi diversi e lo puoi trovare nell'archivio:
http://www.infinitoteatrodelcosmo.it/2018/02/07/cio-avreste-voluto-sapere-quei-paradossali-gemelli/
Certo Vincenzo, sono convinto che "nella RR non è chi viaggia che misura un tic tac più rallentato sul suo orologio, ma è chi vede l'orologio di quello che viaggia"!
Quello di cui vorrei essere certo (ma direi che lo sono) è che affermare: il TEMPO in fisica è proprio il CONTEGGIO dei tic tac di un orologio non è una castroneria :-)
certamente sì... un tic tac che può essere anche quello del cuore o della crescita della barba e via dicendo... e' un invariante fondamentale, come l'energia a riposo, ossia la massa. Ricordiamoci sempre, però, che il tempo è lo stesso per TUTTI: il tempo proprio è quello che si misura sul proprio orologio e quello non cambia a qualsiasi velocità si vada:
Oddio... "il tempo è lo stesso per TUTTI" mi suona strano.... forse devo intendere "esiste un tempo che ciascun osservatore può calcolare conoscendo le velocità relative e sul quale siamo tutti d'accordo" almeno finché restiamo tutti su sistemi di riferimento inerziali. Intendo correttamente, almeno nell'ambito RR?
Caro Francesco,
il tempo proprio è quello che viene misurato da una sola persona, sia che viaggi sia che stia fermo (viaggiare o stare fermo è un qualcosa di relativo, ovviamente). E questo tempo è uguale per tutti, anche per il fotone. Il tempo rallenta solo per chi ha bisogno di un altro osservatore del suo sistema per misurare il tempo di chi si muove rispetto a lui. Ciò capita per chi si muove rispetto a noi: io faccio scattare il mio orologio, ma per controllare quanto tempo è passato per il viaggiatore ci vuole un osservatore situato in un'altra posizione. Questa misura ci dà il tempo improprio del viaggiatore, ossia quello che misuriamo noi in un altro sistema di riferimento.
Scusa se te lo dico, ma non sarebbe male se riuscissi a comprare il mio libro "la favola di Muo", dove ho spiegato nei minimi dettagli i sistemi di riferimento, utilizzando l'orologio a "pallina" di Galileo e quello "a luce" di Einstein,,, Non voglio farmi pubblicità (anche perché non ci guadagno quasi niente), ma penso sia molto utile con tutte le sue figure. Lo trovi, nel caso, nella sezione LIBRI.
Chiaro Vincenzo, grazie.
RR (e RG) le avevo studiate a suo tempo all'università, ora, quasi pensionato, dopo aver dimenticato tutto, cerco di (ri)farmi una cultura. Abbi pazienza, è che pensando ai gemelli la tua affermazione "il tempo è lo stesso per TUTTI" mi ha lasciato spiazzato. Ma è chiaro, qui si cambia sistema di riferimento, e in questi casi il tempo non è uguale per tutti. Se sbaglio mi corrigerete :-)
nessun problema e nessuna scusa. Qui siamo un gruppo di amici che cerca di aiutarsi uno con l'altro a tenere aperto il famoso paracadute di Albert