21/01/16

QUIZ: componiamo le velocità… ***

Il problema è molto semplice…

Noi, osservatori, stiamo in un sistema di riferimento S (a due coordinate x e y). Un sistema di riferimento S’ si muove rispetto a noi con velocità v verso destra lungo l’asse x (x positive), come schematizzato in Fig. 1. Tutto ciò che è visto dal sistema S’ ha l’apice e tutto che ciò è visto da S non ha l’apice.

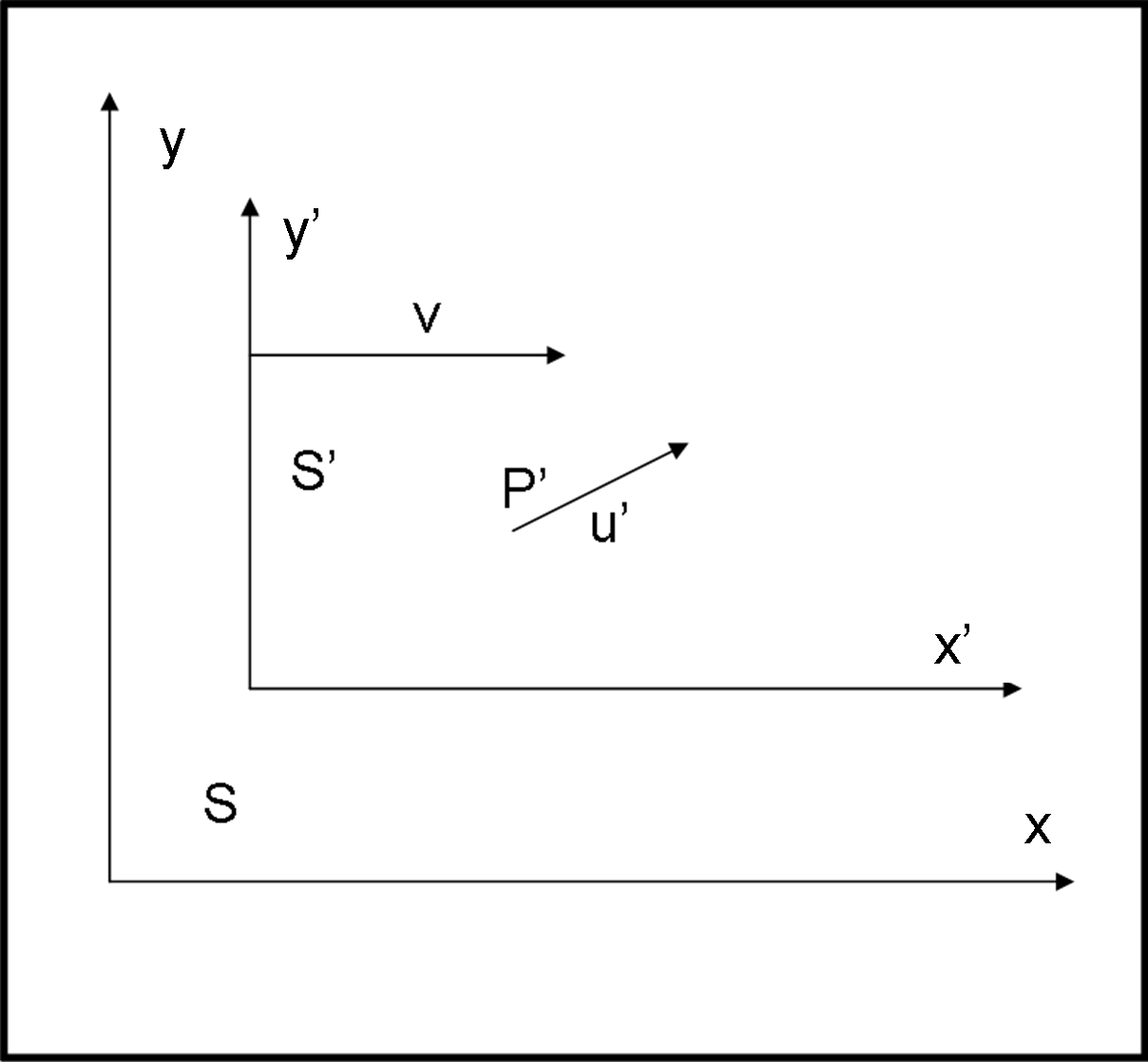
Immaginiamo, adesso, che un oggetto P’ si muova nel sistema S’ con una certa velocità u'.

Proponiamo tre casi:

(1) Il corpo P' si muove solo parallelamente all’asse x’, verso destra, con velocità u’_x parallela a v.

(2) Il corpo si muove solo parallelamente all’asse y’, verso l’alto, (y' positive) con una velocità u’_y, ortogonale a v.

(3) Il corpo si muove in diagonale con una certa velocità u’, tale che le sue componenti lungo x’ e y’ siano proprio u’_x e u’_y.

Per ogni caso, calcolare la velocità del corpo P’ vista da S, ossia u_x, u_y e u sia nel caso della relatività galileiana, sia nel caso della relatività ristretta.

Se volete, per rendervi conto praticamente delle contrazioni e/o estensioni, potete anche inserire dei valori numerici (considerate pure c = 1).

Particolare importanza, nel caso relativistico, è riflettere sulle differenze tra le componenti u_y, nei tre casi. Esse sono le più importanti per la determinazione della quantità di moto relativistica.

Se la domanda non è ben chiara, ditemelo subito: sapete che spesso e volentieri dimentico o sbaglio qualcosa…

Buon lavoro!

P.S.: ho potuto proporre il quiz solo ora, dopo che i nostri grandi informatici (SMA, Peppe e Umberto) hanno introdotto la possibilità di scrivere le formule matematiche nei commenti.

16 commenti

umberto

21/01/2016 at 18:51

domani sveglia presto..sembra tu mi abbia letto nel pensiero; meglio arrivare per gradi ad una cosa così complessa tramite piccoli quiz che esporla subito direttamente, anche se concettualmente (calcoli a parte) sto più pensando a dove si andrà a parare
Vincenzo Zappalà

22/01/2016 at 04:52

caro Umberto,

avevi ragione tu... me ne sono convinto...

E presto detto: calcolare la velocità effettiva di un corpo quando è visto da un qualsiasi altro sistema di riferimento! Abbiamo bisogno della velocità se vogliamo correggere la massa in funzione di lei... E questo è un punto in cui molti divulgatori cadono!!!

Buon lavoro...
umberto

22/01/2016 at 09:11

Non so se faccio bene: parto dal caso generale in cui entrambi le componenti sono diverse da zero, e ottengo gli altri due casi azzerando una o l'altra

Per Galileo:

$U_{x}=U'_{x}+v$

$U_{y}=U'_{y}$

(la componente ortogonale al moto relativo non viene alterata)

Con Pitagora ottengo il modulo della velocità:

$U=\sqrt{(U'_{x}+v)^{^{2}}+U_{y}'^{2}}$

Per Einstein:

$U_{x}=\frac{U'_{x}+v}{1+\frac{v}{c^{2}}U'_{x}}$

$U_{y}=\frac{U'_{y}+v}{1+\frac{v}{c^{2}}U'_{x}}\sqrt{1-\frac{v^{2}}{c^{2}}}$

$U^{2}=U_{x}^{2}+U_{y}^{2}=((U'_{x}+ v)^{2}+U_{y}'^{2}(1-\frac{v^{2}}{c^{2}}))\cdot \frac{1}{(1+\frac{vU'_{x}}{c^{2}})}$

caso 1) si muove parallelamente all'asse x'

U'y=0

Galileo:

$U_{x}=U'_{x} +v$

$U_{y}=0$

$U=U'_{x}+v$

Einstein:

$U_{x}=\frac{U'_{x}+v}{1+\frac{v}{c^{2}}U'_{x}}$

$U_{y}= 0$

U=Ux

caso 2)

U'x=0. si muove solo solo parallelamente all’asse y’

Galileo:

Ux=v

Uy=U'y

$u=\sqrt{v^{2}+U'_{y}^{2}}$

Einstein:

Ux=v

$U_{y}=U'_{y}\sqrt{1-\frac{v^{2}}{c^{2}}}$

$u=\sqrt{v^{2}+(1-v^{2}/c^{2})U'^{2}_{y}}$

spero non ci siano troppi errori; sembrava facile, ma bisognerà esercitarsi molto con le formule Latex
Vincenzo Zappalà

22/01/2016 at 14:34

caro Umberto,

hai ragione il latex è una bella grana... ma...

Non dico niente, ovviamente... ma comincia a riflettere su come varia la componente y a seconda dei casi... E' un esercizio interessante...
umberto

23/01/2016 at 06:41

A parte il fatto che ho visto già due errori nella mia esposizione (nel caso generale nella Uy c'è un +v che non centra niente, nella U manca un quadrato) non riesco bene a capire cosa devo guardare

1)Nel primo caso U'y=0 e quindi anche Uy=0 e non c'è altro da dire

2)Nel secondo è Ux=0, quindi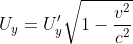 $U_{y}=U'_{y}\sqrt{1-\frac{v^{2}}{c^{2}}}$

3)nel caso generale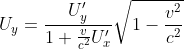 $U_{y}=\frac{U'_{y}}{1+\frac{v}{c^{2}}U'_{x}}\sqrt{1-\frac{v^{2}}{c^{2}}}$

Vedo che nel 3) caso di velocità con entrambi le componenti la Uy è ridotta, rispetto al caso 2) di un fattore che però al massimo può essere 1/2

Nei casi 2) e 3) se v si avvicina a c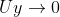 $Uy \to 0$
umberto

23/01/2016 at 07:19

Il tutto si aggancia all'ultimo suggerimento del muro-proiettile

in entrambi i casi, dal punto di vista relativistico, la Uy se v è grande tende a zero.

Il modulo della velocità no, mancando il fattore gamma nel calcolo della velocità:

per v grande U diventa sempre più grande. Invece in Galileo no, Uy è sempre la stessa. Per distruggere il muro la massa deve in qualche modo aumentare dello stesso fattore gamma. E aumenta perchè aumenta il modulo della velocità
Vincenzo Zappalà

23/01/2016 at 08:27

caro Umberto, a parte gli errorini di cui sono un ottimo conoscitore , volevo solo far notare come la componente y si restringa al crescere della velocità v. Nel caso in cui la u' è solo diretta in senso ortogonale vi è un solo fattore correttivo. Nel caso in cui esista anche una componente u'x , la contrazione è ancora più evidente, dato che ci sono due fattori correttivi (uno che dipende, come prima solo dalla velocità tra i sistemi e l'altro che dipende anche da u'x)... Tutto lì... niente di speciale...
Paolo

24/01/2016 at 02:49

Caro Enzo torno ora dal pianeta Papalla e mi ritrovo un quiz relativistico..

Per provare a risolverlo avrei potuto usare, almeno nel primo caso, la formuletta: U = (v + u')/(1+ vu'/c²).

Dove U è la velocità del corpo P' misurata dal sistema “fermo”

(U= Δ x/Δ t) e u' da quello in movimento (u'= Δ x'/Δ t').

Ovviamente ciò è vero solo nel primo caso dove tutti gli spostamenti avvengono solo lungo i rispettivi assi x, ossia il corpo P' si muove lungo l'asse x' per S' e lungo l'asse x per S.

Come al solito voglio complicarmi la vita e ricavare quella famosa formuletta, sconosciuta a Galileo, che avrebbe brutalmente sommato le due velocità.... così facendo, però, nel caso di velocità relativistiche, la somma poteva dare come risultato una velocità maggiore di quella della luce e ciò è decisamente impossibile.

Per far ciò parto dalle trasformazioni di Lorentz:

x’ = (x – vt)/√(1 – β²)............ ma 1/√ (1 - β²) = γ

x’ = (x – vt) γ

Ricavo il valore di x :

x’/γ = x – vt

x = x’/ γ + vt

Calcolo l'intervallo di spazio Δx (x2 - x1) usando la trasformazione appena ricavata:

Δx = x2 - x1 = x2’/γ + vt2 - x1’/γ - vt1 = (x2’-x1’)/γ +v (t2 - t1)

$\fn_phv \fn_phv \Delta x = x_{2} - x_{1} = x'_{2}/\gamma + vt_{2} - x'_{1}/\gamma - vt_{1} = (x'_{2}-x'_{1})/\gamma +v (t _{2}- t _{1})$

ma $\fn_phv (x'_{2} - x'_{1}) = \Delta x'$ ............. e........... $\fn_phv (t_{2} - t_{1}) = \Delta t$

Δx = Δx’/γ + v Δt

ma le trasformazioni che legano spazio e tempo sono due e l'intervallo di tempo Δt è lo stesso, quindi ricavo tale valore dalla prima equazione per poi sostituirlo nella seconda:

Δx - Δx’/γ = v Δt

Δt = (Δx- Δx’/γ)/v

A questo punto parto dalla seconda trasformazione di Lorentz per ricavare il tempo t:

t’ = (t – vx/c²)/√(1 – β²).................. ma 1/√ (1 - β²) = γ

t’ = (t - vx/c²) γ

t’/γ = t - vx/c²

t = t’/γ + vx/c²

Calcolo l'intervallo di tempo Δt :

$\fn_phv \Delta t = (t_{2} - t_{1}) = t'_{2}/\gamma + vx_{2} /c^{2} - t'_{1} /\gamma - vx _{1}/c^{2} = (t’ _{2}- t'_{1})/\gamma + v (x_{2} - x_{1})/c^{2}$

ma $\fn_phv (t'_{2} - t'_{1}) = \Delta t'$ ..... e........ $\fn_phv (x_{2} - x_{1})=\Delta x$

Δt = Δt'/γ + vΔx/c²

Ricavo anche Δx:

Δt - Δt'/γ = vΔx/c²

Δx = c²Δt/v- c²Δt'/vγ

Δx + c²Δt'/vγ = c²Δt/v

vΔx + c²vΔt'/vγ = c²Δt

vΔx + c²Δt'/γ = c²Δt

dato che entrambe le trasformazioni di Lorentz si riferiscono al medesimo intervallo di tempo Δt , sostituisco alla relazione appena trovata il valore trovato nell'altra, ossia   Δt = (Δx- Δx’/γ)/v:

vΔx + c²Δt'/γ = c²(Δx- Δx’/γ)/v

v²Δx + c²vΔt'/γ = c²Δx - c²Δx’/γ

c²Δx’/γ + c²vΔt'/γ = c²Δx - v²Δx

c²(Δx’+ vΔt')/γ = Δx (c²- v²)

Δx = c²(Δx’+ vΔt')/γ (c²- v²)

Ora tocca al tempo, dato che nella seconda trasformazione avevamo ricavato che: Δt = Δt'/γ + vΔx/c²

Δt - Δt'/γ ' = v Δx/c²

c²Δt - c²Δt'/γ ' = v Δx

c²Δt/v - c²Δt'/γ'v = Δx

Sostituendo il valore di Δx ricavato dalla prima trasformazione di Lorentz, ossia

Δx = Δx’/γ + v Δt, ottengo:

c²Δt/v - c²Δt'/γ'v = Δx’/γ + v Δt

c²Δt/v - v Δt = Δx’/γ + c²Δt'/γv

Δt (c²/v - v ) = (vΔx’ + c²Δt')/γv

Δt (c² - v² )/v = (vΔx’ + c²Δt')/γv

Δt = (vΔx’ + c²Δt')/γ(c² - v² )

Ora finalmente posso trovare la velocità U del corpo P' visto dal sistema fermo, ossia il suo rapporto Δx /Δt :

U =Δx /Δt = (c²(Δx’+ vΔt')/γ (c²- v²))/(vΔx’ + c²Δt')/γ(c² - v² )

U =c²(Δx’+ vΔt')/(vΔx’ + c²Δt')

La velocità del punto P' vista dal sistema in movimento era: u' = Δx'/Δt', per cui Δx'=u'Δt'

U =c²(u'Δt' + vΔt')/(vu'Δt' + c²Δt')

U = c² Δt' (v+ u')/Δt' (v u'+ c²)

U = c² (v+ u')/(v u'+ c²) divido sopra e sotto per c²

U = c²/c² (v+ u')/(v u'/c² + c²/c² )

U = (v+ u')/(v u'/c² +1)

Questa in realtà però è valida se P' si muove solo parallelamente all'asse x', ossia rappresenta la componente x della velocità:

$\fn_phv U_{x} = (v+ u'_{x})/(v u'_{x}/c^{2} +1)$

Tutti questi passaggi mi servono ora per trovare le tre componenti spaziali della velocità del corpo P' in movimento nel sistema S' il tutto visto dal sistema fermo (S).

La velocità del corpo P' nella sua componente y è data da:

$\fn_phv u'_{y}= \Delta y'/\Delta t'$

Il sistema S' però si muove solo nella direzione dell'asse x, per cui le trasformazioni di Lorentz indicano che y= y' e quindi Δy' = Δy, ne segue che:

$\fn_phv u'_{y}= \Delta y'/\Delta t' = \Delta y/\Delta t'.$ ....da cui ricavo: $\fn_phv \Delta y = u_{y}\Delta t'$

la componente y della velocità del corpo P' visto dal sistema fermo è:

$\fn_phv U_{y}= \Delta y/\Delta t$           sostituendo      $\fn_phv \Delta y = u'_{y}\Delta t'$

$\fn_phv U_{y}= u'_{y}\Delta t'/\Delta t$

ma l'intervallo di tempo Δt è soggetto alle trasformazioni relativistiche, poiché S' si muove... Basta quindi sostituire a Δt il valore ricavato prima applicando le trasformazioni di Lorentz, ossia: Δt = (vΔx’ + c²Δt')/γ(c² - v² )

$\fn_phv U_{y}= u'_{y}\Delta t'/(v\Delta x' + c^{2}\Delta t')/\gamma (c^{2} - v^{2} )$

$\fn_phv \fn_phv U_{y}= u'_{y}\Delta t'\gamma (c^{2} - v^{2} )/(v\Delta x' + c^{2}\Delta t')$    divido sopra e sotto per c²Δt'

$\fn_phv \fn_phv \fn_phv U_{y}= (u'_{y}\Delta t'\gamma (c^{2} - v^{2} )/(c^{2}\Delta t')/(v\Delta x' + c^{2}\Delta t')/c^{2}\Delta t'$

$\fn_phv \fn_phv \fn_phv \fn_phv U_{y}= (u'_{y}\gamma (c^{2}/c^{2} - v^{2}/c^{2} )/(v\Delta x'/c^{2}\Delta t' + c^{2}\Delta t'/c^{2}\Delta t')$

$\fn_phv \fn_phv \fn_phv \fn_phv \fn_phv \fn_phv U_{y}= (u'_{y}\gamma (1 - v^{2}/c^{2} )/(v\Delta x'/\Delta t'c^{2} + 1)$

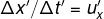ma $\fn_phv \fn_phv \fn_phv \Delta x'/\Delta t' = u'_{x}$          e    γ 1/√(1 - v²/c²)

$\fn_phv \fn_phv U_{y}= u'_{y} (1 - v^{2}/c^{2} )/\sqrt{(1-v^{2}/c^{2})}(vu'_{x}/c^{2} + 1)$

$\fn_phv \large U_{y}= u'_{y}\sqrt{(1-v^{2}/c^{2})}/(vu'_{x}/c^{2} + 1)$

Lo stesso identico discorso si potrebbe fare per trovare la componente z, dato che z'=z e di nuovo uz'= Δz/Δt' per cui si ottiene il medesimo risultato, ossia:

$\fn_phv \large U_{z}= u'_{z}\sqrt{(1-v^{2}/c^{2})}/(vu'_{x}/c^{2} + 1)$

Ora non resta che provare a rispondere ai tre casi del quiz, usando le tre formule ricavate:

1) $\fn_phv \large U_{x} = (v+ u'_{x})/(v u'_{x}/c^{2} +1)$

2) $\fn_phv \large U_{y}= u'_{y}\sqrt{(1-v^{2}/c^{2})}/(vu'_{x}/c^{2} + 1)$

3) $\fn_phv \large U_{z}= u'_{z}\gamma\sqrt{(1-v^{2}/c^{2})}/(vu'_{x}/c^{2} + 1)$

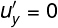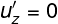
Ne primo caso esiste solo la componente ux' del corpo P', per cui la due e la tre si annullano poiché $\fn_phv \large u'_{y} =0$ e   $\fn_phv \large u'_{z} =0$

Nel secondo caso esiste solo la componente uy' della velocità per cui ux' = 0, ne segue che la 1 e la 3 si annullano, mentre la 2 diventa:

$\fn_phv \large U_{y}= u'_{y} \sqrt{(1 -v^{2}/c^{2})}/(0 + 1) = u'_{y} \sqrt{(1 -v^{2}/c^{2})}$

Nel terzo caso esiste sia la componente uy' che quella ux' della velocità del corpo P' , misurata da S', per cui solo la 3 si annulla dato che uz' = 0, mentre si applicano sia la 1 che la 2.

Partendo dalle stesse tre relazioni provo a ricavare cosa avrebbe detto Galileo, basta porre v/c= 0, ossia considerare velocità trascurabili rispetto alla velocità della luce.

La prima diventa:

$\fn_phv U_{x} = (v+ u'_{x})/(v u'_{x}/c^{2} +1)$

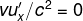
ma $\fn_phv v u'_{x}/c^{2} = 0$

$\fn_phv \large U_{x} = v + u'_{x}$

$\fn_phv \large U_{y}= u'_{y} \sqrt{(1-v^{2}/c^{2})}/(vu'_{x}/c^{2} + 1)$

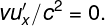ma $\fn_phv \large v u'_{x}/c^{2} = 0.$ ....     e .....          v²/c²=0

$\fn_phv \large U_{y}= u'_{y} \sqrt{1/1} = u'_{y}$

Ossia la componente y della velocità misurata da S rimane tale e quale a quella misurata da S'... d'altronde per Galileo il tempo è assoluto quindi Δt' = Δt.

Spero sia corretto un simile ragionamento... ed ora vado a leggermi i commenti e la complicazione....

Paolo
Vincenzo Zappalà

24/01/2016 at 05:31

bravi Umberto e Paolo che hanno lavorato con un chiaro mio errore relativo al ribaltamento di x con y... Sono proprio imperdonabile!!!!

Conoscendomi, però, hanno subito capito che il problema era nella figura (ora corretta). Riescono ormai a leggermi nel cervello e capire preventivamente i miei soliti errori (accidenti e pensare che guardo e riguardo, ma quando hai una cosa in testa la continui a vedere scritta giusta...).

Ovviamente Paolo è andato oltre ricavando le velocità fin dall'inizio... Un bel ripassone di RR
umberto

24/01/2016 at 14:21

se devo dirti la verità non mi ero accorto dell'errore nella figura..avevo ragionato solo sul testo ed era inequivocabile cosa fossero Ux Uy e v
Vincenzo Zappalà

24/01/2016 at 15:35

lo immaginavo Umberto... Non si sta nemmeno a guardare x e y, tanto la loro posizione è sempre quella... Non so proprio come siano finiti al contrario... mah??!!
Daniela

24/01/2016 at 23:00

Chiedo scusa se mostro la mia soluzione in modo artigianale, ma a quest'ora non ce la faccio a litigare con l'editor delle formule, pertanto potete vedere QUI la sintesi del mio lavoro (e spero che il link funzioni...).
Vincenzo Zappalà

25/01/2016 at 05:28

Dany? ... resti fra noi, ma alle componenti scalari va applicato il teorema di Pitagora per trovare la risultante... che non lo sappiano le belve!!!
Daniela

25/01/2016 at 07:35

Che bischera sono... ho dimenticato la parte più facile... Non ditelo a PapalScherzone, se no mi fa correre intorno a Papallone e chissà dove vado a finire!!

Va beh, almeno ho fatto un bel ripasso di RR
Vincenzo Zappalà

25/01/2016 at 08:34

ne ho fatto tante anch'io di bischerate... se non lo dite voi a papalscherzone starò muto come un pesce!!!
Daniela

25/01/2016 at 08:57

Affare fatto, copriamoci a vicenda!!

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

QUIZ: componiamo le velocità… ***

Articoli correlati

Deflessione della luce per... tutti **

Le trasformazioni di Lorentz

RELATIVISTI 6 : POINCARE' LORENTZ EINSTEIN

Relativisti 5 : Maxwell

16 commenti

Lascia un commento Cancel Reply