Matematiche pure 7):Il campo C dei numeri complessi-Parte seconda ***

Categorie: Matematica Teoria degli insiemi Tags: matematiche superiori Scritto da: Umberto Cibien Commenti:0

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

Riprendiamo il discorso sui numeri complessi; Dopo aver dimostrato che C è un campo, abbiamo visto alcune proprietà :

coniugato di un numero complesso
modulo di un numero complesso
metodo per trovare il reciproco di un numero complesso
Forma trigonometrica di un numero complesso
prodotto di due numeri complessi in forma trigonometrica

Applichiamo quest'ultima per dimostrare la formula di De Moivre:

$(cos\theta +i \cdot sin\theta )^{n}=cos(n\theta )+i\cdot sin(n\theta )$ 1)

metodo molto elegante per calcolare la potenza n-esima di un numero complesso semplicemente considerando un multiplo dell'angolo in rappresentazione trigonometrica.

sia $z=cos\theta +i \cdot sin\theta$ ; sappiamo che il modulo di z,è |z|=1. Vogliamo applicare il principio d'induzione.

Per n=1 la 1) è vera

$z^{1}=cos(1\cdot \theta) +i\cdot sin(1\cdot \theta )$

supponiamola vera per n-1

$z^{n-1}=cos((n-1)\cdot \theta) +i\cdot sin((n-1)\cdot \theta )$

e dimostriamola per n:

$z^{n}=z^{n-1}\cdot z=cos((n-1)\cdot \theta) +i\cdot sin((n-1)\cdot \theta )\cdot (cos\theta +i\cdot sin\theta )$

Sappiamo, dall'articolo precedente, che l'argomento del prodotto è la somma degli argomenti.

calcoliamo tale somma degli argomenti:

$(n-1)\cdot \theta +\theta =n\cdot \theta$

$z^{n}=cos(n\cdot \theta) +i\cdot sin(n\cdot \theta )$ che dà proprio la 1)

Newton e la funzione esponenziale.

Forse pochi sanno che la funzione esponenziale di base e è stata definita in un modo particolare da Newton. Noi tutti oggi sappiamo che la derivata di $e^{x}$ è ancora $e^{x}$ ; questo ci basta per affermare che soluzione dell'equazione differenziale:

$Df(x)=f(x)$ (se il termine equazione differenziale può spaventare pensiamo in questo caso semplicemente ad una equazione in cui l'incognita è una funzione la cui derivata è uguale alla funzione stessa) è proprio la funzione $e^{x}$ . Questo ci è stato insegnato alle superiori, ricavando le derivate fondamentali fra cui proprio quella di $e^{x}$ , a cui ci si arriva tramite il limite fondamentale :

$lim_{z \to 0}\frac{a^{z}-1}{z}=\ln (a)$

essendo ln(e)=1 (logaritmo naturale) nel caso la base della potenza sia e , si ha:

$lim_{z \to 0}\frac{e^{z}-1}{z}=\ln (e)=1$

per calcolare la derivata di $e^{x}$ basta scrivere il rapporto incrementale:

$De^{x}=\lim_{h \to 0} \frac{e^{x+h}-e^{x}}{h}=\lim_{h \to 0} \frac{e^{h}-1}{h}\cdot e^{x}=1\cdot e^{x}=e^{x}$

La soluzione dell'equazione non varia se moltiplichiamo $e^{x}$ per una costante, quindi la soluzione generica è $f(x)=x_{0}\cdot e^{x}$ , dove $x_{0}$ altro non è che il valore della funzione per x=0, essendo $e^{0}=1$ , ovvero $x_{0}$ =f(0).

Queste sono cose che sappiamo però oggi; ai tempi di Newton non si sapevano tutte queste cose sulla funzione esponenziale. Vediamo come procede invece Newton. Il suo problema è quello di risolvere l'equazione differenziale: Df(x)=f(x); ovvero trovare una funzione che sia uguale alla sua derivata.

E qui interviene il genio incomparabile di Newton: Definisce una funzione proprio così, tramite l'equazione differenziale ! Newton procede allora così; La funzione non può essere un polinomio , perchè quando si deriva un polinomio si abbassa di uno il grado (quindi la funzione non potrebbe essere uguale alla sua derivata); però possiamo pensare ad un polinomio infinito, ovvero a una serie. Le serie sono state ampiamente trattate in questo blog, le trovate QUI. Ma continuiamo con il ragionamento di Newton; la nostra soluzione sarà una certa funzione, ma ogni funzione (sotto determinate condizioni) può espressa come una serie del tipo:

$f(x)=\sum_{n=0}^{\infty}c_{n}x^{n}$

Le costanti $c_{n}$ sono date dallo sviluppo di Taylor - Mc Laurin

$c_{0}=f(0);c_{1}=Df(0);c_{2}=\frac{D^{2}f(0)}{2!};...; c_{n}=\frac{D^{n}f(0))}{n!}$ e questa è una cosa;

ma il fatto che la derivata della funzione coincida con la funzione stessa, provoca questa catena:

$Df(x)=f(x)$

$D^{2}f(x)=Df(x)$

...

$D^{n+1}f(x)=D^{n}f(x)$ che porta a:

$D^{n+1}f(x)=D^{n}f(x)=....Df(x)=f(x)$

in particolare, se calcoliamo in zero le derivate successive, si ha:

$D^{n+1}f(0)=D^{n}f(0)=....Df(0)=f(0)$ ;

tornando adesso ai coefficienti dello sviluppo, essendo $c_{n}=\frac{D^{n}f(0)}{n!}$ ma essendo il valore della derivata n-esima indipendente da n ed uguale a f(0), otteniamo che $c_{n}=\frac{f(0)}{n!}$ qualsiasi sia n;( notiamo che f(0) è un valore arbitrario ,nei problemi di fisica è quello che si definisce valore iniziale). Quindi possiamo , nella serie $f(x)=\sum_{n=0}^{\infty}c_{n}x^{n}$ ; raccogliere f(0), ottenendo:

$f(x)=\sum_{n=0}^{\infty}c_{n}x^{n}=f(0)\cdot \sum_{n=0}^{\infty}\frac{x^{n}}{n!}$ ; bene allora definiamo :

$e^{x}= \sum_{n=0}^{\infty}\frac{x^{n}}{n!}$ e di conseguenza, calcolando la funzione in 1:

$e^{1}= \sum_{n=0}^{\infty}\frac{1^{n}}{n!}= \sum_{n=0}^{\infty}\frac{1}{n!}=1+\frac{1}{2}+\frac{1}{3!}+\frac{1}{4!}+....=e$

quindi abbiamo anche definito il numero e, oltre a un metodo per calcolarlo.

Definizione di esponenziale complesso.

Il fatto di aver definito $e^{x}$ come somma di una serie in campo reale, ci permette di estendere in modo naturale la definizione nel campo complesso:

Definiamo esponenziale complesso la funzione:

$e^{z}= \sum_{n=0}^{\infty}\frac{z^{n}}{n!}$ dove z è un numero complesso.

Questo ha senso perchè l'insieme dei numeri complessi è un campo, e in esso sono definite le operazioni di somma, prodotto, elevamento a potenza, rapporto.

Richiami sullo sviluppo in serie di seno e coseno

(in tutti questi esempi prendiamo per buono il fatto che le serie che trattiamo convergano, ovvero che abbiamo somma finita, per qualsiasi valore della variabile x)

Ricordando l'espressione della serie :

$f(x)=\sum_{n=0}^{\infty}c_{n}x^{n}$

Le costanti $c_{n}$ sono date dallo sviluppo di Taylor- Mc Laurin

$c_{0}=f(0);c_{1}=Df(0);c_{2}=\frac{D^{2}f(0)}{2!};...; c_{n}=\frac{D^{n}f(0))}{n!}$

se consideriamo la funzione sin(x), avremo:

$c_{0}=sin(0)=0;c_{1}=cos(0)=1;c_{2}=\frac{-sin(0)}{2}=0; c_{3}=-\frac{cos(0)}{6}=-\frac{1}{6}$ .....

per cui $sin(x)=x-\frac{x^{3}}{6}+\frac{x^{5}}{120}+...$

vogliamo ora esprimere il termine generico della serie con una espressione funzione di n;

notiamo il coefficiente del termine pari è nullo perchè (lasciando per ora da parte i segni)partendo dal seno se derivo una volta ottengo il coseno, se derivo due volte ottengo il seno; siccome devo calcolare la funzione in zero, il seno di zero è zero. Il coefficiente pari dunque è nullo, quello dispari è unitario ma il segno parte da 1 (cos(0)) poi diventa -1 (-cos(0)=-1) e così via. Sappiamo poi che a denominatore abbiamo il fattoriale dell'esponente.

Il termine generico della serie è pertanto $\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}$ come potete verificare sostituendo a n i valori 0,1,2,ecc. Infatti:

$\frac{(-1)^{0}}{(2\cdot 0+1)!}x^{2\cdot 0+1}=\frac{1}{( 1)!}x^{1}=x$ per n=0

$\frac{(-1)^{1}}{(2\cdot 1+1)!}x^{2\cdot 1+1}=-\frac{x^{3}}{3!}=-\frac{x^{3}}{6}$ per n=1

$\frac{(-1)^{2}}{(2\cdot 2+1)!}x^{2\cdot 2+1}=\frac{x^{5}}{5!}=\frac{x^{5}}{120}$ per n=2 e così via.

Quindi in definitiva possiamo scrivere:

$sin(x)=\sum_{0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}x^{2n+1}$

Analogo discorso vale per il coseno; qui sono invece i termini pari ad essere diversi da zero.

$cos(x)=1-\frac{x^{2}}{2}+\frac{x^{4}}{4!}+.....(-1)^{n}\frac{x^{2n}}{(2n)!}$

in questo caso il termine generale è $(-1)^{n}\frac{x^{2n}}{(2n)!}$

calcoliamo i primi valori.

$(-1)^{0}\frac{x^{0}}{(0)!}=1$ per n=0

$(-1)^{1}\frac{x^{2}}{(2)!}=\frac{x^{2}}{2}$ per n=1

$(-1)^{2}\frac{x^{2\cdot 2}}{(2\cdot 2)!}=\frac{x^{4}}{4!}$ per n=4

l'espressione compatta diventa:

$cos(x)=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!}$

riassumendo: lo sviluppo di sin(x) mi dà tutte le potenze dispari, quello di cos(x) tutte le potenze pari. In entrambi i casi, la potenza viene divisa per il fattoriale dell' esponente. Viene in mente una cosa; sovrapponendo (sommando) le due serie si ottiene una serie di potenze per così dire "completa":

$1+x -\frac{x^{2}}{2}-\frac{x^{3}}{6}+\frac{x^{4}}{4!}+ \frac{x^{5}}{120}+...$ che assomiglia molto allo sviluppo in serie dell'esponenziale:

$1+x +\frac{x^{2}}{2}+\frac{x^{3}}{6}+\frac{x^{4}}{4!}+ \frac{x^{5}}{120}+...$ a parte i segni. Forse è stata proprio questa somiglianza a spingere Eulero nel cercare una relazione fra esponenziale e funzioni trigonometriche; ma per trovarla non bastavano i numeri reali, doveva cercarla nei numeri complessi.

La formula di Eulero

La formula di Eulero è (assieme all'identità di Eulero che vedremo appena dopo) una delle formule più belle della matematica. Essa esprime il legame fra la funzione esponenziale di base e (numero di nepero) in C e la forma trigonometrica di un numero complesso; supponiamo che $x$ sia un numero reale,

allora ix è un numero complesso (immaginario puro); la funzione :

$e^{ix }$

sarà una funzione a valori complessi ; infatti è somma della serie: $e^{z}= \sum_{n=0}^{\infty}\frac{z^{n}}{n!}$
Sappiamo poi che qualsiasi numero complesso si può scrivere in forma trigonometrica come:

$cosx +isinx$ ; ebbene la formula di Eulero ci dice che:

$e^{ix}=cosx +isinx$

Dimostriamo la formula partendo dalla definizione di esponenziale complesso. Abbiamo definito l'esponenziale complesso come:

$e^{z}= \sum_{n=0}^{\infty}\frac{z^{n}}{n!}$

Consideriamo adesso un numero complesso immaginario puro, ovvero z=iy.

$e^{iy}=\sum_{n=0}^{\infty} \frac{i^{n}y^{n}}{n!}$ (abbiamo semplicemente scritto iy al posto di z nello sviluppo $e^{z}= \sum_{n=0}^{\infty}\frac{z^{n}}{n!}$ )

Spezziamo adesso la serie $\sum_{n=0}^{\infty} \frac{i^{n}y^{n}}{n!}$ in due parti (esponenti pari e esponenti dispari) $\sum_{n=0}^{\infty} \frac{i^{n}y^{n}}{n!}=\sum_{n=0}^{\infty} \frac{i^{2n}y^{2n}}{(2n)!}+\sum_{n=0}^{\infty} \frac{i^{2n+1}y^{2n+1}}{(2n+1)!}$ 1);

nel primo addendo abbiamo infatti tutte le potenze pari : $\sum_{n=0}^{\infty} \frac{i^{2n}y^{n}}{(2n)!}=1+\frac{i^{2}y^{2}}{2}+\frac{i^{4}y^{4}}{4!}+...$

nel secondo $\sum_{n=0}^{\infty} \frac{i^{2n+1}y^{2n+1}}{(2n+1)!}=i +\frac{i^{3}y^{3}}{3!}+\frac{i^{5}y^{5}}{5!}+...$ tutte le potenze dispari (basta sostituire ad n i valori 0,1,2,3,...)

osserviamo che $i^{2n}=(i^{2})^{n}=(-1)^{n}$

mentre $i^{2n+1}=i\cdot i^{2n}=i\cdot (-1)^{n}$

quindi possiamo riscrivere la 1) :

$\sum_{n=0}^{\infty} \frac{i^{n}y^{n}}{n!}=\sum_{n=0}^{\infty} \frac{(-1)^{n}y^{2n}}{(2n)!}+i\cdot \sum_{n=0}^{\infty} \frac{(-1)^{n})y^{2n+1}}{(2n+1)!}$

Usiamo adesso i due sviluppi di seno e coseno che abbiamo calcolato sopra:

$cos(x)=\sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n)!}$ ; $sin(x)=\sum_{0}^{\infty} \frac{(-1)^{n}}{(2n+1)!}x^{2n+1}$ ; confrontando con la formula sopra otteniamo subito che:

$e^{iy}=\sum_{n=0}^{\infty} \frac{i^{n}y^{n}}{n!}=cos(x)+isin(x))$

Identità di Eulero.

Eccoci arrivati all'identità di Eulero; essa non è altro che un caso particolare della formula:

$e^{ix }=cosx +isinx$

quando $x=\pi$ ; la formula diventa:

$e^{i\pi }=cos\pi +isin\pi=-1+0=-1$ ovvero:

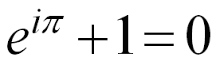
L' identità di Eulero resta una delle formule più belle della matematica; Richard Feynman disse che questa formula era straordinaria perchè legava fra di loro le maggiori entità della matematica: il numero zero (elemento neutro per la somma), il numero uno, identità per il prodotto; il numero irrazionale p-greco e il numero irrazionale e; l'unità immaginaria i , la somma e l'elevamento a potenza.

Per chi vuole esercitarsi

La trattazione teorica permette di affrontare tutte le problematiche di base sui numeri complessi. La didattica vera e propria esula dagli obiettivi di questi articoli. Per chi non li ha mai visti, per impratichirsi sarebbe meglio esercitarsi. C'è un ottimo sito dove trovate esercizi da svolgere o completamente svolti:Esercizi sui numeri complessi .

L	M	M	G	V	S	D
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Matematiche pure 7):Il campo C dei numeri complessi-Parte seconda ***

Articoli correlati

Il Problema di Apollonio e le "sue" coniche. 3 **/***

Il Problema di Apollonio e le "sue" coniche. 2 **/***

Un grillo innamorato, Fibonacci e la prosodia indiana **

Il problema di Apollonio e le "sue" coniche. 1 **/***

Lascia un commento Cancel Reply

Il Problema di Apollonio e le "sue" coniche. 3 /*

Il Problema di Apollonio e le "sue" coniche. 2 /*

Il problema di Apollonio e le "sue" coniche. 1 /*