Categorie: Matematica
Tags: costante del cerchio costante della parabola eccentricità geometria parabola pi greco
Scritto da: Vincenzo Zappalà
Commenti:9
Anche la parabola ha il suo pi greco **
Questo articolo è inserito in "Matematica e geometria"
Non ha certo la fama del pi greco, ma anche la parabola, qualsiasi essa sia, è caratterizzata da una costante irrazionale. Per assonanza la chiameremo solo p.
Per quale motivo dovrebbe esistere un tale parametro, invariabile rispetto a qualsiasi forma assuma la curva? Beh... basta pensare alle coniche e, in particolare, al cerchio, che altro non è che un'ellisse molto particolare. Le iperboli e le ellissi sono due famiglie di curve che variano la loro forma in funzione dell'eccentricità. Per tale motivo una possibile similitudine tra curve della stessa famiglia è impossibile.
Il cerchio, invece, è caratterizzato da un'eccentricità sempre uguale, che assume il valor zero. Il che vuol dire che tutti i cerchi hanno la stessa eccentricità e, quindi possono tranquillamente possedere una costante che li caratterizza tutti. Questa costante la conosciamo molto bene e può essere descritta come il rapporto tra la lunghezza della circonferenza e il diametro del cerchio. Scriviamo questa relazione e abbiamo:
costante cerchio = circonferenza/diametro = 2πr/2r = π
Abbiamo scoperto l'acqua calda, ovviamente! La costante cercata non è altro che il celeberrimo pi greco, gioia e dolore di tanti scienziati greci e non solo.
Consideriamo, adesso, la parabola. Essa può essere più o meno aperta, ma mantiene comunque SEMPRE la stessa eccentricità che risulta essere uguale a UNO. Così come il cerchio poteva aumentare o diminuire il proprio raggio ma manteneva immutata la sua costanza, così la parabola può benissimo avere una sua costante che rimane la stessa qualsiasi sia l'apertura della curva. Proviamo a vedere se esiste...
Per fare ciò richiamiamo (e disegniamo in Fig. 1) la descrizione geometrica di una parabola qualsiasi.
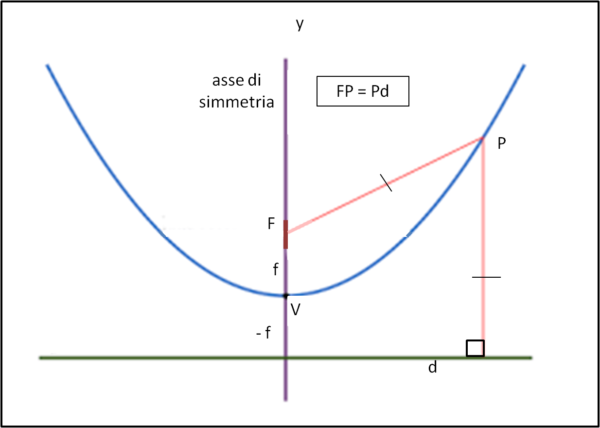
Essa viene definita come il luogo dei punti che ha pari distanza da un punto F, detto fuoco, e da una retta d, detta direttrice. Risulta immediato che per mantenere questa definizione il punto V (vertice), appartenendo alla parabola, deve avere pari distanza da F e dalla retta d. La retta che passa per F ed è perpendicolare a d risulta essere un asse di simmetria, ossia ciò che capita alla sua sinistra deve capitare alla sua destra.
Prendiamo un punto P qualsiasi della parabola e scriviamo in termini matematici l'uguaglianza delle distanze, in modo da ottenere un'equazione della parabola in termini dell'ascissa e dell'ordinata di un suo qualsiasi punto. Senza perdere in generalità, portiamo l'origine dei nostri assi x e y in V, con l'asse x parallelo alla direttrice d e l'asse y coincidente con l'asse di simmetria.
Un punto qualsiasi della parabola ha coordinate P(x,y), mentre il fuoco F ha coordinate F(0, f), dove f è la distanza tra vertice e fuoco ed è anche la metà della distanza tra direttrice e il fuoco. Ne segue che la direttrice ha equazione y = - f (Fig. 2).
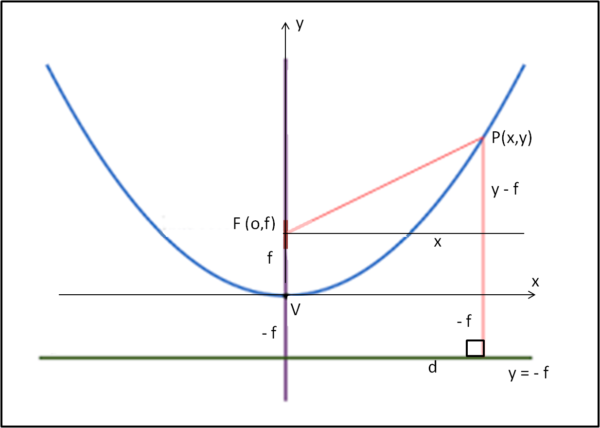
La distanza tra P e direttrice d può essere scritta come
Pd = y - (- f) = y + f
La distanza tra P e il fuoco F può essere scritta, applicando il teorema di Pitagora, come:
PF2 = x2 + (y - f)2
PF = √(x2 + (y - f)2)
Uguagliando le due distanze (Pd e PF, come ci impone l'appartenenza del punto P alla parabola), abbiamo:
y + f = √(x2 + (y - f)2)
Che è l'equazione della nostra parabola. e che possiamo scrivere ancora meglio ricavando y. Quadriamo entrambi i membri
(y + f)2 = x2 + (y - f)2
e svolgiamo i quadrati
y2 + f2 + 2fy = x2 + y2 + f2 - 2fy
Semplificando...
4 f y = x2
y = x2/4f .... (1)
Una simpatica formula per la parabola...
Possiamo, finalmente introdurre la costante della parabola p. Per far ciò, tracciamo da F la parallela a d fino a incontrare la parabola nei punti Q e R (Fig. 3).
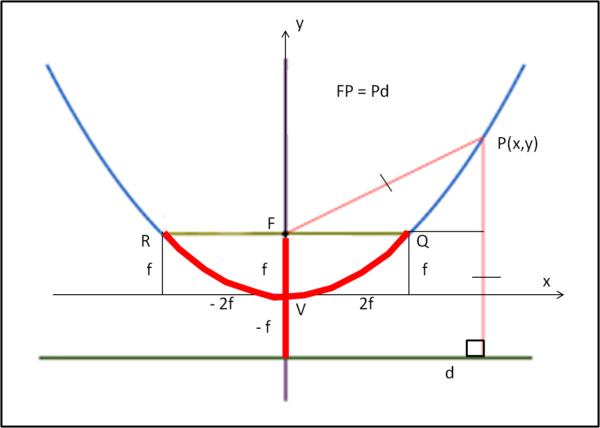
Questi due punti hanno ascissa pari a 2f e - 2f, dato che, appartenendo alla parabola, devono avere pari distanza da d e da F. Ma Qd = Rd = 2f e quindi anche la distanza RF = QF = 2f. Ne segue che Q(2f, f) e R(-2f, f)
Definiamo come costante p della parabola il rapporto tra l'arco di parabola RVQ e il segmento Fd = 2f:
p = RVQ/2f .... (2)
Siamo giunti al primo punto critico... Come calcolare la lunghezza di un arco di curva? Bene, esiste una formula che per adesso prendiamo per buona e che fa ovviamente uso dell'integrale. Essa dice che la lunghezza di un arco tra due punti è l'integrale, definito tra le ascisse dei due punti estremi, della radice quadrata di uno più il quadrato della derivata della funzione di cui vogliamo calcolare l'arco. Nel nostro caso, ricordando la (1):
RVQ = ∫-2f2f√(1 + (dy/dx)2 dx = ∫-2f2f√(1 +(d(x2/4f)/dx)2 dx = ∫-2f2f√(1 +(x/2f)2)dx = ∫-2f2f√(1 +(x2/4f2) dx
Da cui:
p = (1/2f) ∫-2f2f√(1 +(x2/4f2) dx .... (3)
Siamo arrivati al secondo punto critico. Infatti, l'integrale non è cosa semplice e per risolverlo bisogna "trafficare" parecchio. Vi sono vari modi per farlo sia attraverso la trigonometria, sia attraverso le funzioni iperboliche. Per non appesantire questo articolo che vuole essere molto divulgativo, prendiamo per buona la soluzione dell'integrale e scriviamo:
p = ln(1 + √2) + √2
Svolgendo i calcoli, otteniamo:
p = 2. 29558714939...
Come il pi greco, anche questo numero è irrazionale e trascendente.
9 commenti
Caspita Enzo! Davvero interessante l'esistenza di questa costante della parabola, grazie per avercela fatta notare.
Mi incuriosisce il fatto che pi greco lo troviamo dappertutto nelle equazioni della nostra fisica e questa costante no. In altre parole: perché il cerchio è la più 'importante' delle coniche?
Probabilmente sì, Francesco... forse gli è pari l'ellisse, ma lei non può avere costante. Il cerchio è una figura perfetta che ha per molto tempo descritto la traiettoria dei pianeti oltre che rappresentare la classica forma di equilibrio
Caro Enzo,
l'argomento mi ha incuriosito e così mi sono permesso di postare un esempio numerico (sperando di non aver fatto male i calcoli).
Ho considerato, per semplicità, la funzione di parabola con i coefficienti a=1 e b=c=0,
ovvero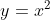
il suo Δ = 0 (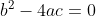
) e ricordando le coordinate del fuoco )
e l'equazione della direttrice
l'ordinata di F è pari a 1 /4 e la retta direttrice (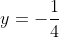
) interseca l'asse y nel punto F' = (0, - 1 / 4)
e la distanza FF' sarà pari a 2 × 1 / 4 = 1 / 2.
L'arco AB presenta una lunghezza pari all'integrale definito tra - 1 / 2 e 1 / 2 di radice di 1 più la derivata al quadrato della funzione di parabola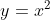
→ 
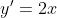→ ^2=4x^2)
l'integrale indefinito (in forma semplificata) sarà:
(come faceva notare Enzo, per calcolare l'integrale indefinito si può ricorrere alla sostituzione della x con una determinata funzione trigonometrica o iperbolica, ma non è il caso di complicare le cose);
allora l'arco di parabola AB =-ln(4\sqrt2-4)}}{4})
(1)
Consideriamo i 2 termini logaritmici al numeratore della (1):
siccome ln(A) - ln(B) = ln(A / B), si può scrivere:&space;-&space;ln(4&space;\sqrt2&space;-&space;4)&space;=&space;ln\frac{4&space;\sqrt2&space;+&space;4}{4&space;\sqrt2&space;-&space;4})
isoliamo l'argomento del logaritmo naturale e moltiplichiamo numeratore e denominatore per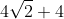
il denominatore diverrà un prodotto notevole, il numeratore il quadrato di un binomio
ma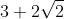
= ^2)
(quadrato di 
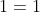, quadrato di 
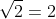, doppio prodotto 
)
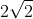in definitiva: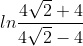
= ^2)
= )
la (1) si potrà scrivere: AB =
= 
la costante parabolica sarà uguale al rapporto tra AB e FF', ma FF' = 1 / 2 per cui dividere per un mezzo equivale a moltiplicare per 2, per cui p = √2 + ln(1 + √2) come ha già scritto Enzo.
Fantastico Enzo e fantastiche le Scienze Matematiche!!!
P.S.
Non conoscevo l'esistenza della costante parabolica, ma grazie ad Enzo ed ai suoi articoli scritti in maniera sempre impeccabilmente chiara, semplice e comprensibile (molto meglio di testi scolastici e/o universitari "sponsorizzati") ogni giorno, per chi ha voglia e curiosità, si apprende un quid di sapere in più...
PP.SS.
Caro Enzo, se non ricordo male, la lunghezza di un tratto di curva si può ottenere considerando un punto x della curva e i suoi incrementi infinitesimi, applicando poi il teorema di Pitagora ai dx e dy "incrementati"...
Ti ringrazio caro Andy, soprattutto per l'ottimo lavoro che hai eseguito. Ma anche per la tua illuminante e costante presenza! Sì il metodo è quello che dici tu e si arriva al risultato in modo non troppo difficile. Magari ci torniamo sopra...
Ricorderò sempre il primo compito in classe di disegno tecnico di prima liceo scientifico; professoressa Penzo-Gradara, uno dei 4 quiz era: disegnate il luogo geometrico dei punti del piano ewuidistanti da un punto P e da una retta R... Ovviamente le coniche non erano ancora state affrontate né in matematica, né in disegno.
ottimo esercizio, Dario !
Sig.Vincenzo Zappalà,
ho visionato le spiegazioni di cui sopra e non ho trovato quanto mi riproponevo; avevo digitato " se esista un qualche rapporto geometrico fra la tripla pitagorica 3-4-5 e la Parabola completa " )e mi sono trovato qui nel vostro Blog.
Consentitemi di proporvi una mia interpretazione e tralascio ,per ora la dimostrazione, come dalla tripla si ottenga , la: [( X^2-4X+2)=0] che è somma di altre due parabole pitagoriche.
Ciò che m'interessa è di segnalarvi che nelle figg 1,2,3 ,relative alla costruzione per punti ,appartenenti alla parabola ,si è omesso un punto importante che non appartiene alla parabola ma che consente di costruirla proprio partendo dal fuoco F che è un punto appartenente alla circonferenza del cerchio in cui è inscritto il triangolo retto 3-4-5 pitagorico.
Nel caso della Parabola ,che ho indicato qui sopra ,il fuoco è nientemeno che il Centro del cerchio di cui sopra di raggio 5/2=2,5
Va da sé che costruito il cerchio di raggio 5/2=2,5 troverete che la circonferenza interseca i due rami della parabola ,poi ,puntando con lo stesso raggio nel punto d'intersezione ottenuto sul ramo destro (puntoB)
di coord. (3.5 ; 3,25) tracciate un arco fra il fuoco F ed il punto che si trova sulla verticale del punto B sulla direttrice(punto D); poi prolungate la verticale in basso fino ad intersecare la circonferenza nel punto C.
Infine ,unite tale punto al punto (O) del sistema degli assi cartesiani e ottenute due informazioni.
Si materializza il triangolo retto della tripla 3-4-5 semplicemente tracciando un segmento parallelo alla direttrice passante per B ed A che appartiene sia alla parabola sia all'ipotenusa con pendenza negativa.
Infine notate che la retta passante per O e C passa anche per il fuoco F ; fatto che non emerge dalle figure 1-2-3
perché quelle parabole hanno il loro asse di simmetria giacente su quello degli assi cartesiani.
Nel caso che vi sottopongo invece si tratta del caso generale di parabola completa del tipo [aX ± bX ± c =0]
Questa Parabola offre due soluzioni interessanti su cui ,se avrò riscontro, indicherei altre proprietà delle due soluzioni x‛ e x‟.
Cordialità.☯️
Joseph 11 ✍️(giuseppelucianof@gmail.com)
Torino li, 11/8/23⏳
grazie Giuseppe per il contributo...
Vi trovo per la prima volta, dopo aver cercato approfondimenti sulla parabola. Non sapevo dell' esistenza dell' invariante p, grazie utilissimo.
Francesco