Categorie: Fisica classica Storia della Scienza
Tags: Cavendish Costante di gravitazione universale densità Densità della Terra legge di gravitazione universale pendolo a torsione
Scritto da: Vincenzo Zappalà
Commenti:0
Cavendish e la densità della Terra **
Questo articolo è inserito in Dinamica e Meccanica, all'interno di Fisica Classica
Newton scoprì una legge fondamentale e soprattutto universale per spiegare il moto dei pianeti e non solo, ma non riuscì mai a determinare il valore della sua costante G. Dovette quindi accontentarsi solo di rapporti di forze, in modo da eliminare quella scomoda costante. Valori relativi, insomma, ma non assoluti (praticamente lo stesso "problema" incontrato da Keplero con le sue leggi, che stabiliscono il rapporto tra le distanze dei pianeti, ma non il loro valore assoluto, come abbiamo spiegato QUI).
Analogamente non riuscì mai a determinare la massa della Terra, dato che restava legata a quella costante G. Trafficando con la sua legge è, infatti, facile scrivere:
GMT = gRT2
g e RT potevano essere determinati e stimati, ma tutto ciò che si otteneva era solo e soltanto il prodotto tra la massa della Terra e la costante G. In realtà, sembra che a Newton interessasse poco il valore di G.
Vi era un solo modo per poter ricavare G "staccandolo" dal valore della massa terrestre o solare o quello che volete, ossia quello di misurarlo attraverso l'utilizzo di masse "artificiali" conosciute. Newton ci pensò un po' su e tristemente concluse che "Neppure intere montagne sarebbero però sufficienti a provocare effetti sensibili".
Il valore di G fu ricavato solo un secolo e mezzo dopo e non grazie a montagne, ma a sofisticatissimi strumenti di laboratorio e a piccole masse che, però, non servirono subito a determinare G, bensì la densità della Terra. Insomma, la storia di G è una lunga avventura nella quale il ruolo del protagonista è ricoperto dall'esperimento di Henry Cavendish del 1797-98 ed è questo che ci accingiamo a descrivere.
Prima, però, è giusto far sapere che esiste qualcuno che resta nell'ombra nella storia del celebre esperimento. Questa figura è quella del geologo, astronomo e sismologo John Michell, il quale ideò proprio l'apparecchiatura per misurare la densità della Terra ma che non utilizzò mai a causa della sua morte. Cavendish ne fu colpito e riuscì, con la sua meticolosa precisione, a utilizzarla con grande successo. Non pensiamo, però, che abbia cercato di "rubare" l'idea! Cavendish inizia il suo meticoloso lavoro, pubblicato nel 1798 (meriterebbe leggerlo per capire la straordinaria accuratezza del suo approccio), dicendo chiaramente che l'idea e l'apparecchiatura era stata di Michell e che lui aveva solo effettuato l'esperimento attraverso tutta una serie di azioni e di misure che gli avevano permesso di rendere minimi gli errori strumentali e le condizioni ben lontane da quello del vuoto assoluto. Riportiamo, a conferma di ciò, le sue parole di introduzione:
"Many years ago, the late Rev. John Michell, of this Society, contrived a method of determining the density of the earth, by rendering sensible the attraction of small quantities of matter; but, as he was engaged in other pursuits, he did not complete the apparatus till a short time before his death, and did not live to make any experiments with it. After his death, the apparatus came to the Rev. Francis John. Hyde Wollaston, Jacksonian Professor at Cambridge, who, not having conveniences for making experiments with it, in,the manner he could wish, was so good as to give it to me (Molti anni fa, lo scomparso Rev. John Michell, di questa Società, escogitò un metodo per determinare la densità della Terra, rendendo sensibile l'attrazione di piccole quantità di materia: ma, essendo coinvolto in altre problematiche, egli non riuscì a completare l'apparato fino a poco prima della sua morte, e non ebbe tempo per tentare qualche esperimento. Dopo la sua morte, l'apparato passò nelle mani del Rev. Francis John Hyde Wollaston, professore a Cambridge che, non avendo intenzione di utilizzarlo, fu così gentile da darmelo)"
Prima di lasciare nuovamente nell'ombra Michell, ricordiamo anche che lui fu il primo a prospettare l'esistenza di "stelle nere", ossia tali da esistere senza essere viste, dato che la luce non poteva lasciarle...
Ciò non toglie, comunque, che Cavendish si accorse che l'apparecchiatura andava ancora migliorata nel modo che desiderava e che le misure pre-esperimento dovevano raggiungere precisioni ai limiti per quei tempi. Lo svolgimento dell'esperimento (ma sarebbe meglio dire degli esperimenti) fu meticoloso, ripetitivo, attento ad ogni problema potesse sorgere come, ad esempio, una qualche forma di magnetismo tra le masse coinvolte. Nel lavoro originario si spiegano tutti questi accorgimenti e si danno i risultati numerici, tralasciando praticamente la parte teorica e il ruolo della costante gravitazionale (G). Cavendish, infatti, ottenuta la sicurezza dei suoi risultati si limita a dire:
"By a mean of the experiments made with the wire first used, the density of the earth comes out 5,48 times greater than that of water; and by a mean of those made with the latter wire, it comes out the same; and the extreme difference of the results of the 23 observations made with this wire, is only ,75; so that the extreme results do not differ from the mean by more than ,38, or 1/14 of the hole, and therefore the density should seem to be determined hereby, to great exactness. ("Per mezzo degli esperimenti compiuti con il primo filo, la densità della Terra risulta 5.48 volte quella dell'acqua; lo stesso risultato si ottiene utilizzando un secondo filo; la differenza più grande di queste 23 osservazioni è solo ,75; da cui risulta che i risultati estremi non differiscono dalla media di più di ,38 o 1/14 e, perciò, la densità sembrerebbe ottenuta con grande esattezza...)".
Proprio l'esperimento di Cavendish solleva un problema che esiste tuttora tra i metodi usati negli esperimenti dei grandi della Scienza e quelli che vengono descritti attraverso formule più o meno complesse. Il titolo stesso del lavoro originario di Cavendish mette in chiara luce il problema: Esperimento per determinare la densità della Terra. Oggi, invece, si ci riferisce ad esso come "Determinazione della costante di Gravitazione G". Una differenza molto importante che apre le porte a una discussione ben più ampia che Daniela affronterà più a fondo.
Per il momento resta inequivocabile il fatto che Cavendish si disinteressava completamente della determinazione di G, mentre invece le trattazioni "didattiche" odierne mostrano varie forme di calcolo, tutte dirette essenzialmente alla deduzione del valore di G, da cui poi sarebbe seguito facilmente il valore della massa della Terra e, quindi, la sua densità (tra le varie trattazioni disponibili in rete non possiamo non richiamare la vostra attenzione sulla differenza abissale tra la correttezza dell'esposizione di Wikipedia inglese e quella di Wikipedia italiana che definire approssimata e superficiale è fin troppo generoso... leggete e capirete senza bisogno di ulteriori commenti).
No, Cavendish ha svolto l'esperimento senza minimamente pensare a G, anzi facendolo scomparire attraverso un rapporto tra due forze gravitazionali. E' giusto travisare attraverso calcoli e formule "moderne" ciò che venne realmente svolto dagli Scienziati? Qualcosa di simile coinvolge anche il contesto storico ed umano in cui operavano gli scienziati. Descrivere meglio la vita, le intuizioni e le peculiarità dei vari caratteri diventa informazione fondamentale per una visione ad ampio respiro dell'importanza e dei risvolti collegati alle scoperte fondamentali della Scienza.
Sicuramente Cavendish è riuscito a raggiungere certi risultati proprio grazie a un suo carattere che amava in modo estremo la precisione, la pazienza, la ripetizione e l'analisi dettagliata di qualsiasi possibile intoppo. Vale, perciò, la pena di raccontare la sua vita per mostrare quanto sia stata a volte oltre al limite della normalità. Come abbiamo già detto nel quiz di "antipasto", in fondo, in fondo, per avere idee geniali o per eseguire esperimenti che sembrerebbero andare oltre i limiti, bisogna essere un po' "particolari"...
Su cosa si basava l'apparecchiatura? Beh... su una forza che noi da bambini (quando ancora non si potevano uccidere decine e decine di alieni con i videogiochi e non si viveva nel mondo virtuale dei social che rendono sempre più vaghi i confini tra un uccisione virtuale e una reale) cercavamo di sfruttare al massimo per far volare aerei o elicotteri o per solcare le acque con zattere di compensato o di balsa...

Oggi si trovano sicuramente in commercio (guai far pensare i bambini), ma una volta il bello era proprio costruirseli da soli. Il concetto "fisico" è molto semplice: si lega l'elica o le pale della zattera a un elastico e si comincia a ruotare in modo che l'elastico continui a girare su se stesso e immagazzini un momento torcente che viene poi liberato quando si lascia libero il "motore"... La rotazione che ne deriva, in verso contrario a quella da noi impartita, può permette spostamenti del nostro velivolo o natante che allora sembravano infinite e prodigiose.
Stiamo parlando della cosiddetta "bilancia a torsione" ossia solo e soltanto di un filo che regge un solido o, nel nostro caso, un'asta ai cui due estremi sono poste delle palline di uguale massa. Si chiama anche pendolo a torsione in quanto il movimento finale è un moto armonico. Infatti, ruotando l'asta, il filo che la sorregge si torce. Una volta lasciata libera, essa accelera e torna nelle condizioni iniziali, ma le supera per inerzia, raggiungendo nuovamente un massimo di torsione. Tenta, perciò, di riportarsi ancora nelle condizioni iniziali e via dicendo in un moto che senza attriti continuerebbe indefinitamente. In pratica ne risulta un moto armonico smorzato che si ferma, alla fine, ritornando nelle condizioni iniziali. Qualcosa di veramente molto simile alle oscillazioni di un classico pendolo. La determinazione del periodo di oscillazione è una misura fondamentale, dato che esso ci dice quanto vale una certa costante di torsione tipica del filo utilizzato.
Ed ecco, allora, l'idea di Michell, portata avanti e applicata da Cavendish: la torsione del filo che regge l'asta con le due palline viene introdotta attraverso la forza di gravitazione universale, inserendo due sfere di massa uguale ma decisamente più pesanti delle altre. Anche se tutto il sistema risente della gravità terrestre, è possibile estrarre la piccolissima componente dovuta all'attrazione delle sfere artificiali e, conoscendone la massa, risalire alla densità della Terra.
Facile a dirsi, ma ben più difficile a farsi, dato che il tutto deve essere isolato al massimo da perturbazioni esterne e, quindi, è necessario non solo inserire ogni componente con una precisione assoluta, ma anche non interferire mai con l'apparato che deve essere mosso a distanza. Bisogna poi permettere alle oscillazioni di smorzarsi completamente: un lavoro in cui non si deve avere fretta e in cui ogni mossa deve essere controllata.
Come spesso capita negli esperimenti antichi si tende oggi a realizzarli con tecnologie e con formulazioni matematiche diverse. Così è successo con l'esperimento di Cavendish. Chi volesse realmente seguire passo dopo passo la versione originale può divertirsi a leggere il suo lavoro.
L'apparato di Cavendish (modernizzato) è illustrato molto bene in questo breve video.
Notiamo come la parte dell'oscillazione del pendolo sia oggi facilmente risolvibile, mentre Cavendish aveva dovuto studiare attentamente l'oscillazione attraverso lo spostamento del raggio riflesso su intervalli di tempo discreti.
Questo, invece, uno schema dell'apparato originale:
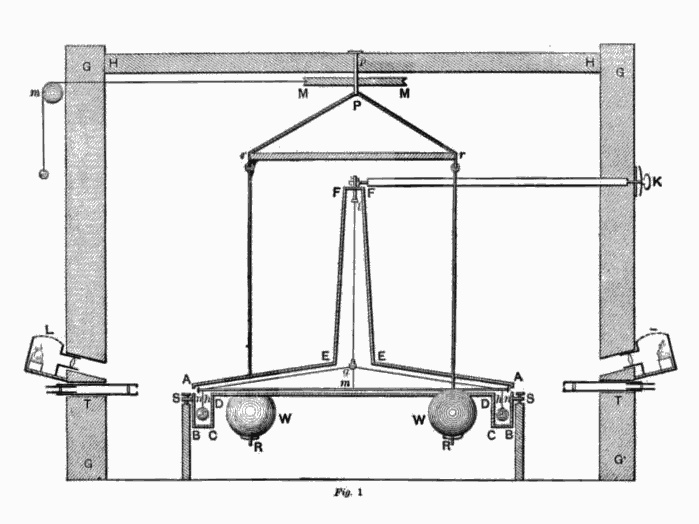
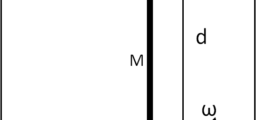
Cerchiamo di schematizzare il tutto in Fig. 1
La massa più piccola sia m; il filo a cui sono sospese deve essere posizionato esattamente nel baricentro H del sistema composto dalle due masse m più l'asta che le congiunge. Fondamentale è già a questo punto stabilizzare il nostro pendolo a torsione. A questo punto inseriamo a una certa distanza le due masse M più grandi in modo che non possano muoversi.
Cosa succede? Le due masse M attirano a sé le due masse più piccole e producono una torsione nel filo che le sostiene, Questa torsione, o meglio, questo momento torcente è uguale e contrario a quello determinato dalla rotazione delle due masse m. In altre parole, il filo è soggetto a una forza elastica che è uguale e opposta a quella gravitazionale che ha fatto avvicinare le palline. Possiamo scrivere:
FE = -FG = - GmM/r2
r è la distanza tra le palline m e quelle più pesanti M. L'asta con le due palline si posiziona con uno spostamento angolare rispetto alle condizioni iniziali pari a φ.
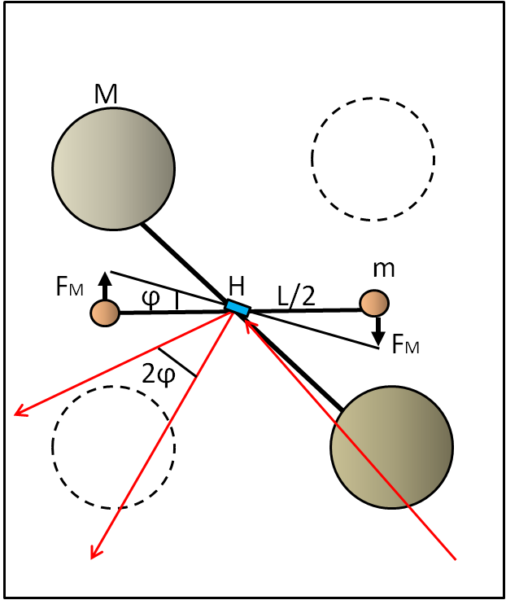
Ogni filo, però, ha una sua risposta alla coppia torcente e quindi è legato all'angolo φ attraverso una certa costante di torsione k. Possiamo scrivere:
τ = k φ
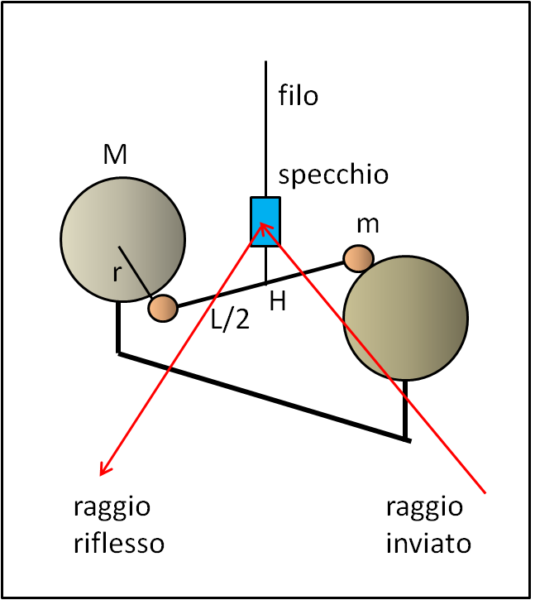
Come leggere, però, l'angolo φ? Ed eccoci al piccolo quiz estivo. Viene inserito uno specchietto solidale col filo e si invia una raggio di luce su di esso, in modo che avvenga una riflessione che colpisca un certo regolo graduato. Spostando lo specchietto, a causa della torsione del filo, il raggio di ritorno si sposta di 2φ.
La semplice dimostrazione è data in Fig. 3
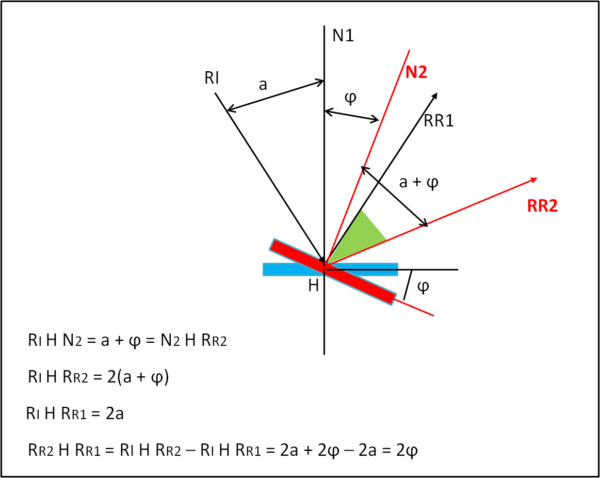
Questa è perciò una quantità misurabile con grande precisione. Nel frattempo si deve conoscere la costante di torsione del filo. Ma essa si può dedurre dal periodo di oscillazione del filo dopo avergli impresso una rotazione e averlo lasciato libero di raggiungere l'equilibrio. Una misura non facile, ma fondamentale.
Per avere ulteriore conferma dell'ampiezza dell'angolo di spostamento dell'asta che unisce le due masse piccole, si ruotano le due masse grandi di 180° in modo che si vengano a trovare dalla parte opposta rispetto alle masse piccole m (alla stessa distanza r). L'asta, con lo specchietto, che aveva "immagazzinato" la coppia torcente del primo spostamento dovuto alla forza gravitazionale, si trova adesso sotto l'azione di questa forza e della nuova forza di gravitazionale impressa dalla nuova posizione delle masse M. Lo specchietto farà, perciò, un doppio percorso attorno alla posizione di equilibrio e darà un nuovo valore di φ (le forze in gioco sono sempre le stesse).
Non resta che legare la coppia torcente, ormai nota, alla forza gravitazionale che ha mosso le palline di massa m verso quelle di massa M. Si scrive facilmente che τ, il momento della coppia dovuta alle forze FM , vale:
τ = FM L/2 (forza per il braccio di una singola massa m)
La forza FM, però, deve seguire la legge di Newton. Si hanno così a disposizione alcune lunghezze e angoli misurabili (L, φ, r), una costante calcolata (k). Ovviamente si conoscono anche le masse delle palline grandi e quindi la forza gravitazionale dovuta alla Terra sulla pallina di massa M. La forza tra le palline di diversa massa è stata calcolata attraverso il pendolo a torsione e all'angolo di spostamento, per cui ne segue che applicando nuovamente la legge di Newton si può fare il rapporto tra le due forze, ricavando l'unica incognita, ossia la massa della Terra o -ancor meglio- la sua densità, conoscendone il raggio. Non compare, perciò, né la costante G e nemmeno la massa della pallina piccola. Infatti:
FT = G m MT/rT2
FM = G m M/r2
Il loro rapporto R è conosciuto dato che sono conosciute le forze e quindi:
(GmMT/rT2)/(G m M/r2) = R
MT = R M rT2/r2
Esprimendo le masse in funzione dei volumi e della densità, si ottiene direttamente il valore della densità terrestre, conoscendo quella della pallina di massa M.
Il metodo seguito è quello che forse si avvicina maggiormente a quello realmente seguito da Cavendish, anche se lui aveva dovuto visualizzare il moto del pendolo attraverso il grafico dell'accelerazione del moto dell'immagine riflessa sul regolo in funzione del tempo.
E, finalmente, si accontentano non solo i topografi, ma anche fisici, astronomi e geologi che quel valore hanno cercato per tanto tempo. Già nel 1772, infatti, la Royal Society aveva costituito un apposito Comitato che raggiunse, sì, un risultato, ma secondo Cavendish (che aveva anche partecipato alla progettazione dell'esperimento) ben poco attendibile in quanto viziato da assunti (sulla densità relativa della Terra rispetto alla montagna oggetto dell'esperimento e della stessa montagna rispetto all'acqua) non verificati sperimentalmente e che incidevano in modo determinante sul valore ottenuto. Ci viene spontaneo chiederci cosa penserebbe Cavendish dei programmi che vengono fatti girare oggi su potenti computer per "dimostrare" l'esistenza della materia oscura, infarciti di assunti vari...
Ho lasciato volutamente la descrizione fisica un po' nel vago, ribadendo i concetti base più che le formule NON usate da Cavendish. In realtà, se cercate in rete "esperimento di Cavendish" trovate innumerevoli metodi, più o meno complicati, per trovare le formule risolutive. Essi rappresentano però trascrizioni moderne di un concetto portato avanti in modo ben diverso da Cavendish. Per chi volesse andare più a fondo e vedere in quanti modi si può oggi descrivere l'esperimento accomunandogli formule nate molto dopo, consiglio questo sito (vi accorgerete, però, che danzando nel web, ogni autore utilizza un metodo più o meno diverso, avendo però sempre come scopo finale la derivazione di G).
Vi è forse paura di svilire le grandi scoperte mettendo in chiaro la semplicità e apparente approssimazione degli approcci? In fondo anche la legge di Newton è nata senza bisogno di equazioni differenziali, ma da un confronto quasi banale tra caduta della Luna e caduta di una pietra (vedi QUI e QUI). No, non vogliamo iniziare una rivoluzione didattica, ma per una volta limitiamoci a dare i concetti e le operazioni base dell'unico sperimentatore, tralasciando le versioni preparate successivamente per i posteri.
Resta il fatto indiscutibile che un esperimento che sembrerebbe oltre al limite del fattibile per la fine del '700, è stato possibile (lo stesso metodo si utilizza ancora oggi) grazie alla caparbietà, la calma e la precisione finalizzate principalmente alla ricerca (e alla conseguente eliminazione) di tutte le possibili perturbazioni e fonti di errore. Il valore da lui trovato ha un errore rispetto alle misurazioni odierne decisamente piccolo rispetto al valore attuale: 5.45 (il suo 5.48 riportato nel lavoro originario sembra infatti dovuto a un errore di stampa (?)) contro 5.51 g/cm3 (*).
(*) In realtà, l'errore maggiore è dovuto probabilmente al fatto che non si tiene conto della forza di gravità che la pallina di massa M esercita anche sulla pallina di massa m più lontana.
NEWS! Nel 2021, con un'apparecchiatura simile a quella utilizzata da Cavendish, si è misuratala curvatura dello spaziotempo dovuta ad una massa delle dimensioni di una coccinella