Inizia un progetto piuttosto ambizioso: la traduzione in modo molto libero -e ridotto- di alcune delle celeberrime lezioni sulla fisica base di Richard Feynman, tenute alla Cornell University dal 1961 al 1964. Un giusto ricordo di chi ha cercato, con tutto se stesso, di impartire interesse e capacità di ragionamento nei futuri uomini di pensiero. Tempo perso? Forse sì, ma mi basterebbe che anche un solo giovane trovasse spunto per cambiare la visione succube e passiva della propria esistenza.

Le lezioni di Fisica di Feynman sono disponibili in questa pagina https://www.feynmanlectures.caltech.edu/ all'interno della quale troverete anche le registrazioni originali delle lezioni introduttive ai principali argomenti, le cui traduzioni libere costituiscono la base di questo progetto.

INTRODUZIONE GENERALE (del tutto personale)

Conosciamo tutti molto bene Richard Feynman, premio Nobel per la Fisica e ideatore del celebre esperimento della doppia fenditura, giudicato uno degli esperimenti di fisica più "belli" in assoluto. Di lui abbiamo riportato la meravigliosa descrizione della Elettrodinamica Quantistica (QED) che mette in luce attraverso esempi estremamente divulgativi il magnifico gioco tra fotoni ed elettroni e come esso domini tutta la materia che popola l'Universo.

Rimangono anche celebri le sue lezioni di Introduzione alla Fisica tenute al Caltech tra il 1961 e il 1964, dove i principi fondamentali sono descritti in modo quasi "spiazzante" per la loro semplicità e per il modo spesso anticonvenzionale con cui vengono affrontati. Insomma, un vero piacere leggerli e un grande aiuto per capire certi fenomeni e meccanismi fondamentali che talvolta rimangono con un velo di incomprensione nei normali trattati di fisica. Sarebbe cosa obbligatoria  ascoltare le sue lezioni per chiunque voglia arrivare all'insegnamento della fisica. Per cui, su suggerimento di Daniela, mi sono deciso di appoggiarmi al grande Maestro e riproporre alcune "chicche" delle sue lezioni. Vedremo che saranno estremamente utili per capire i concetti fondamentali e per affrontarli con quel velo di ironia che Feynman regala sempre nei suoi approcci spesso veramente innovativi e inaspettati.

la mia traduzione sarà molto libera e un poco personalizzata (non certo per migliorare Richard, ma solo per estrarre gli argomenti più incisivi e accorciare una trattazione altrimenti decisamente troppo lunga da affrontare in questa sede). Iniziamo con un capitolo fondamentale per la storia della Scienza. la GRAVITA'. Gli esempi fatti da Richard usano le misure inglesi (pollici, piedi, miglia) per cui ho approssimato certi valori nelle nostre unità, permettendomi perciò di essere talvolta poco preciso. Tuttavia, la vera essenza delle lezioni è quella di descrivere i concetti e, quindi, poco importa l'approssimazione che ne verrà fuori.

LA GRAVITA'

Questa lezione vuole mettere in luce la vera storia della legge di Newton e di come il grande genio sia pervenuto ad essa, senza  banali retoriche, e si basa essenzialmente sulla celebre frase: "La Luna continua a cadere verso la Terra". Egli ci spiegherà in maniera semplice e un poco approssimata come questo concetto indirizzò Newton nella stesura della sua legge. Non cerchiamo quindi la perfezione che sarà raggiunta lentamente negli anni a venire.

Per dare subito un esempio dell'ironia che pervade tutta la lezione, ripropongo pari pari una frase di Feynman:

"Cosa dice la legge di gravitazione? Dice che ogni oggetto dell'Universo attrae qualsiasi altro oggetto con una forza che, per ogni coppia di oggetti, è proporzionale alle loro masse e varia con l'inverso del quadrato della distanza tra loro. Se a questa enunciazione si aggiunge il fatto che un oggetto risponde alla forza che subisce accelerando, nella direzione della forza, di una quantità che è inversamente proporzionale alla sua massa, noi avremmo detto tutto il necessario per permettere a un matematico di sufficiente talento di dedurre tutte le conseguenze di questi due principi. Tuttavia, dato che si assume che voi non siate ancora matematici di talento, discuteremo di queste conseguenze nei loro dettagli, senza lasciarvi alle prese con i soli principi base. Ne consegue che descriveremo brevemente la storia della scoperta di questa legge e discuteremo di alcune delle sue conseguenze più importanti, dei suoi effetti sulla storia, dei misteri che essa racchiude e, molto rapidamente, dei ritocchi a cui è stata soggetta da Einstein.

Al di là dell'apparente sottile ironia riguardo ai semplici "ritocchi" di Einstein, Feynman vuole mettere in evidenza che la legge di gravitazione Universale resta un punto fondamentale di tutta la Scienza, un momento di generalizzazione mai avvenuta precedentemente. In particolare, per descrivere esattamente tutto ciò che l'uomo comune riesce a percepire nello spazio che lo circonda, la legge di gravitazione è un risultato eccezionale. Solo l'avvicinamento al micro e al macrocosmo, impossibile tecnicamente a Newton, ha potuto portare alla teoria della Relatività Generale. Ricordiamo che lo stesso Einstein, durante la sua trattazione sia di relatività ristretta che generale continua a dimostrare come sotto condizioni "normali" (ossia per velocità di molto inferiori a quelle della luce e lontani da masse enormi, del tutto impensabili ai tempi di Newton) il suo spaziotempo curvo possa sempre essere descritto con le leggi enunciate da Newton. In qualche modo, cerca sempre una prova che quello che sta facendo ricada nella visione di Newton. La frase "ironica" di Feynman sui "ritocchi" è quindi un segno di stima assoluta verso il genio di Newton. D'altra parte le imprese spaziali che si affidano solo e soltanto alle sue leggi ne sono una prova tangibile.

Un po' di storia

La storia della legge di gravitazione universale inizia con osservazioni degli antichi riguardanti il moto dei pianeti rispetto alle stelle che apparivano fisse. Una grande fatica che, attraverso periodi di genialità e di stasi (più frequenti per varie ragioni non scientifiche), alla fine ha portato alla consapevolezza del moto dei pianeti attorno al Sole, ossia alla così detta Rivoluzione Copernicana. Tuttavia, restava ancora da capire come i pianeti si muovessero attorno al Sole. Durante il sedicesimo secolo si sollevò un grande dibattito tra i favorevoli e i contrari alla visione copernicana. In questo contesto Tycho Brahe ebbe un'idea portentosa, diversa da tutto quanto era stato fatto precedentemente: solo se i dati osservativi fossero stati davvero accurati si sarebbe potuto risolvere veramente la questione e rifiutare le ipotesi fallaci.  In altre parole, Tycho si convinse che era molto meglio cercare di ottenere dati estremamente precisi piuttosto che discutere più o meno "filosoficamente" sulla consistenza delle idee.

Una decisione davvero rivoluzionaria, che rompeva decisamente con quanto si era fatto fino ad allora, quando certe leggi dovevano sempre obbedire a principi di vario tipo che spesso con la Scienza avevano poco a che fare. Egli iniziò a osservare i pianeti per molti anni dall'isola di Hven, vicino a Copenhagen, riportando le loro posizioni ultra precise su tabelle che riempirono volumi, un suo regalo ai posteri e alle menti capaci di usarli come discriminanti per la determinazione della migliore descrizione scientifica. Pur mantenendo le sue idee in proposito, Tycho fornì lo strumento perché venissero confermate o confutate.  Quelle tavole vennero usate da un suo allievo che dopo la sua morte successe a lui, tale Giovanni Keplero... L'analisi dei dati di Brahe lo portò a formulare una teoria puramente eliocentrica e alla formulazione di tre leggi empiriche che descrivevano in modo semplice, ma rigoroso, i moti dei pianeti (ne abbiamo parlato QUI).

Mentre Keplero scopriva queste leggi, Galileo stava studiando le leggi del moto e scoprì un fatto importantissimo: se qualcosa si muove e niente lo viene a disturbare, esso continua a mantenere la sua velocità costante lungo una linea retta. In poche parole definì il principio d'inerzia.

Newton  sviluppa questa idea dicendo che l'unico modo per far variare il moto di un corpo è quello di applicargli una forza. Se, in particolare, il corpo accelera soltanto vuol dire che la forza agisce nella direzione del moto; se, invece, il corpo cambia direzione, la forza deve essergli applicata lateralmente. Sembrano conclusioni ovvie, ma così non era a quei tempi, dato che il concetto finale era veramente rivoluzionario: per cambiare la direzione di un oggetto o la sua velocità è necessaria una forza.

Per esempio, se una pietra è legata strettamente a una corda, per farla ruotare è necessaria una forza che agisca sulla corda. La sua legge dice, infatti, che l'accelerazione prodotta dalla forza è inversamente proporzionale alla massa della pietra (a = F/m) o, se si preferisce, che la forza è proporzionale alla massa moltiplicata per l'accelerazione. Ciò comporta che un oggetto più massiccio abbia bisogno di una forza maggiore per ottenere la stessa accelerazione.

Come sintesi di tutto ciò Newton espresse una delle sue idee più brillanti: per far ruotare un corpo attorno a un altro è necessaria soltanto una forza diretta lungo la congiungente i due corpi e non vi è assolutamente bisogno di una forza diretta nel verso del moto, dato che la sola forza esercitata dalla corda è più che sufficiente a fargli percorrere la traiettoria circolare. E' ovvia l'applicazione di questo concetto al moto dei pianeti e alle leggi di Keplero.

Se niente li disturbasse, i pianeti si muoverebbero di moto rettilineo uniforme, ma il loro moto devia costantemente e lo fa in direzione ortogonale. A causa del principio d'inerzia deve esistere una forza non diretta lungo il moto rettilineo ma diretta verso il Sole. Ricordiamo che proprio a quei tempi si pensava che fossero degli angeli a spingere i pianeti... beh, se angelo deve essere, esso non è altri che il Sole!

Newton fu estremamente felice che il Sole diventasse fisicamente il centro "direzionale" delle forze che governavano il moto dei pianeti. La seconda legge di Keplero (aree uguali sono "spazzate" in tempi uguali) era un segno preciso che le deviazioni rispetto alla linea retta erano RADIALI.

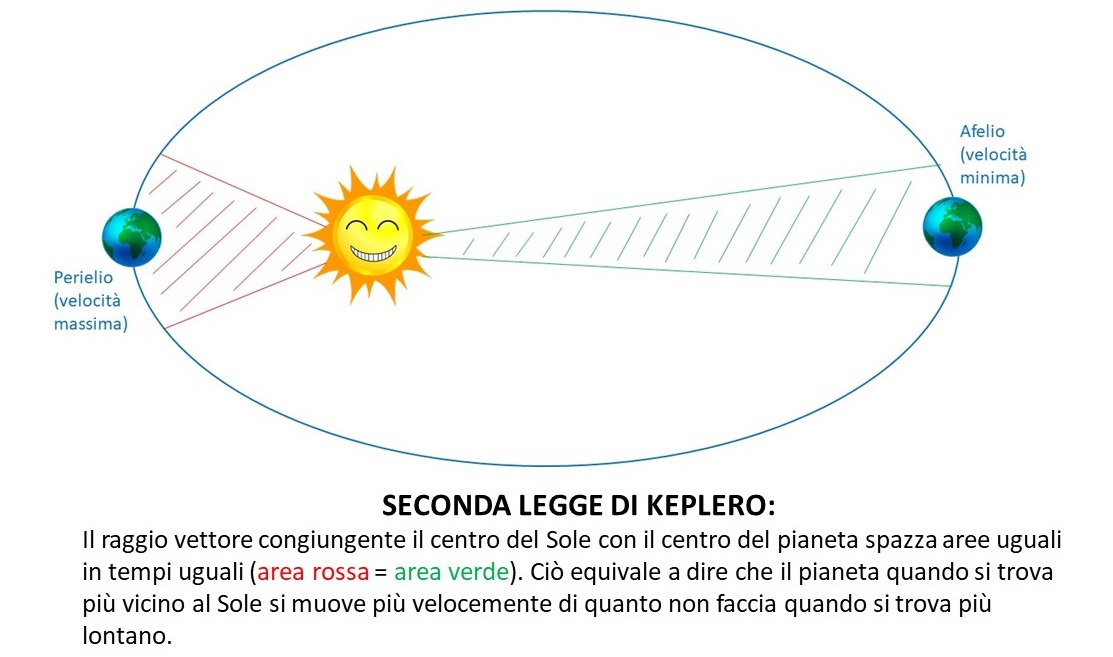
La terza legge gli diceva inoltre che più lontani si andava dal Sole e più debole era la forza. Queste considerazioni non potevano che fargli pensare a una legge che andasse con l'inverso del quadrato delle distanza.

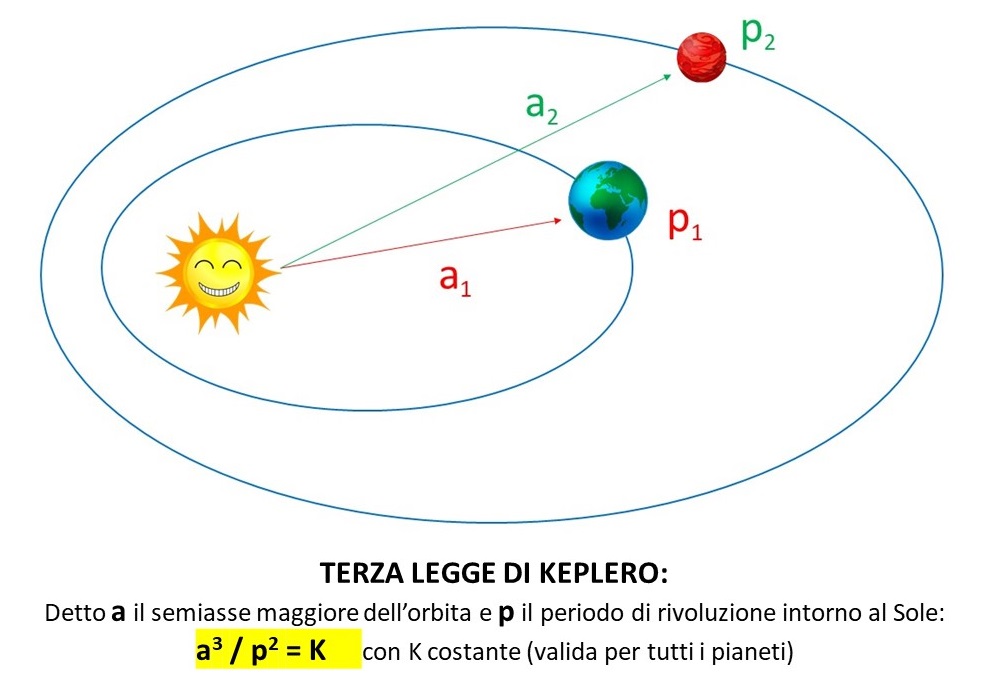
La sua mente, estremamente capace di generalizzare i concetti, gli fece concludere che questo meccanismo doveva essere esteso a tutti i corpi celesti. Già sapeva che qualcosa di estremamente simile accadeva per i satelliti di Giove e che anche le persone erano attratte dalla Terra che avevano sotto i piedi. In poche parole, la legge doveva essere UNIVERSALE: ogni cosa attrae qualsiasi altra cosa.

L'idea della Luna che cade potrebbe sembrare confusa, dato che la distanza rimane la stessa. Tuttavia, Newton basò i suoi calcoli proprio su questo tipo di relazione, considerando come caduta in un certo intervallo di tempo l'allontanamento dalla linea che rappresenta la velocità in un dato punto della sua orbita, ossia quella che la Luna seguirebbe se non le fosse applicata nessuna forza. Conviene sviluppare un po' meglio questo concetto.

Mettiamoci sulla nostra Terra ed eseguiamo un esperimento estremamente semplice, ma altrettanto indicativo. Lo illustriamo in Fig. 1, dove abbiamo a disposizione due palline (potrebbero anche avere massa diversa se potessimo non avere atmosfera, ossia attriti).

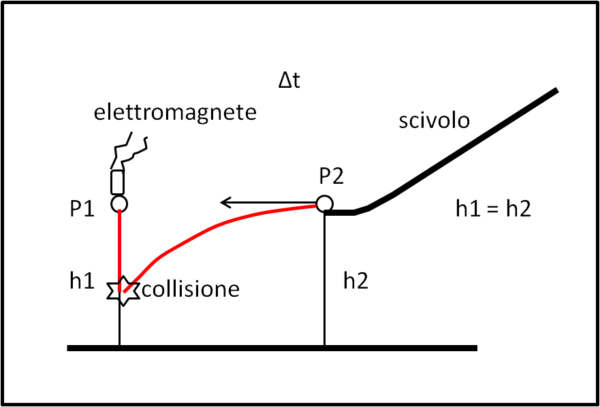
Una di queste, P2, la vogliamo lanciare  in senso orizzontale con una certa velocità v. Per far questo adoperiamo lo scivolo di destra dove la pallina acquista velocità per poi lanciarsi in direzione perfettamente orizzontale. Nel momento in cui si stacca dallo scivolo, un meccanismo fa sì che la seconda pallina P1, trattenuta da un magnete e posta alla stessa altezza della fine dello scivolo, venga liberata e possa cadere solo per effetto della gravità. Cosa fanno le due palline?

Se sono abbastanza vicine e la velocità orizzontale è abbastanza alta, le due palline si scontrano sicuramente prima di raggiungere il suolo. E ciò capita qualsiasi sia la velocità orizzontale della pallina P2. Ovviamente, più è alta la sua velocità e più è alto il punto di incontro tra P1 e P2. Nel caso la velocità  fosse troppo bassa le palline incontrerebbero prima il suolo, ma la loro traiettoria indicherebbe comunque che esse non potevano che incontrarsi. Ciò significa che IN TEMPI UGUALI sia la pallina che cade da ferma sia quella che cade, pur andando a grande velocità orizzontale, CADONO DELLA STESSA QUANTITA' h. In poche parole, il percorso verso il basso della pallina P2 non dipende assolutamente dalla velocità orizzontale che le è stata impartita: qualsiasi essa sia, in un certo intervallo di tempo essa percorre sempre la stessa distanza verso il suolo.

Adesso, però, vogliamo ottenere un risultato apparentemente assurdo: fare cadere sempre la pallina (e questo DEVE capitare), mantenendola  sempre a una certa altezza dal suolo. In parole "moderne" metterla in orbita attorno alla Terra ad una distanza di pochi centimetri o anche sulla sua superficie. L'apparente controsenso della frase relativa alla Luna diventa palpabile: cadere continuamente verso la Terra senza mai toccarla. Si può fare, dando la giusta velocità e questa velocità è calcolabile abbastanza facilmente (con le dovute approssimazioni) attraverso una proprietà del triangolo rettangolo.  In altre parole, possiamo farla cadere in modo tale che mantenga sempre la stessa distanza dal suolo, in particolare a una distanza ZERO dal suolo.

A questo punto, dobbiamo ricordarci che la Terra è rotonda. Non ci resta che imporre che la pallina cada in un secondo della stessa quantità che sarebbe caduta se lasciata libera di cadere senza alcuna velocità. Ad esempio, imponendo che la pallina cada sempre di 5 metri in un secondo. Basta pensare che la Terra è rotonda e che dobbiamo considerare come CADUTA la distanza della pallina dalla traiettoria orizzontale impartita dalla sua velocità. Tradotto in altre parole: quanto deve andare lontana la pallina dal suo punto iniziale affinché in un secondo il suolo si trovi a 5 m sotto tale linea orizzontale? Disegniamo la Terra in Fig. 2, sapendo che il suo raggio è circa 6000 km e che la tangente coincide con la direzione della velocità in P (ovviamente, le proporzioni non sono mantenute!).

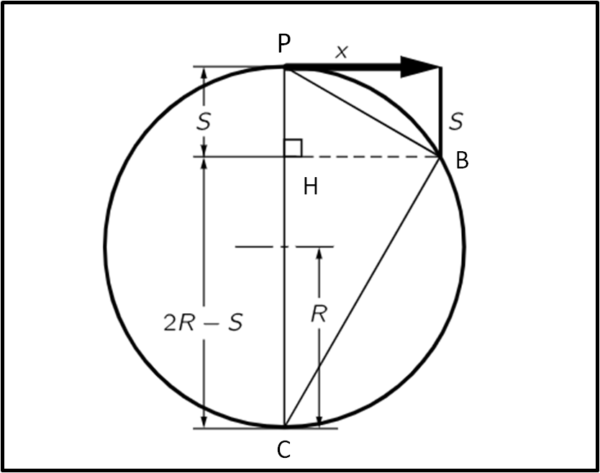
Quello che vogliamo ottenere è la distanza x tale che la distanza S sia proprio uguale a 5 metri, ossia la pallina pur cadendo mantenga sempre la stessa posizione rispetto al suolo terrestre.

Consideriamo il triangolo PBC che è per costruzione rettangolo dato che l'ipotenusa è uguale al diametro della Terra. Sappiamo fin da tempi molto antichi che il segmento BH è medio proporzionale tra PH e HC, ossia:

PH/BH = BH/HC

S/x = x/(2R - S)

Data la piccolezza di S rispetto a R, possiamo approssimare in

S/x = x/2R

x² = 2 SR

x = √(2SR) = √(2 · 6000 · 5/1000) = √60 = 7.7 km

Ossia la velocità orizzontale dovrebbe essere

v = 7.7 km/s

Questa è proprio la velocità che bisognerebbe avere per mettersi in orbita attorno alla Terra rimanendo a zero metri d'altezza (tutte le montagne sono state "piallate" perfettamente). "Ma questa", come dice Feynman, "è anche la velocità che ha permesso a Mr. Gagarin di rimanere sempre alla stessa altezza dal suolo durante il suo viaggio di 40000 km attorno alla Terra (in realtà, un po' più lungo dato che si trovava un po' più in alto)".

Nota: A questo punto consiglio di rileggere questo articolo, dove si calcola in modo decisamente più accurato la velocità necessaria a orbitare a zero metri d'altezza e quest'altro, in cui Feynman dà il meglio di sé in un metodo innovativo relativo allo studio del moto planetario.

Avevamo intenzione di proseguire ma, nel momento in cui abbiamo provato a scrivere il seguito, ci siamo resi conto che il contributo originale alla comprensione della gravità si esaurisce in questa prima parte e andare avanti con una semplice opera di traduzione delle sue lezioni (peraltro già disponibile e facilmente acquistabile anche in rete), non ci sembra avere alcun valore aggiunto per i nostri lettori. Pertanto ci fermiamo qui, accontentandoci di avere aggiunto una gocciolina nell'oceano della divulgazione del Feynman-pensiero!