Questo articolo è stato inserito nell'approfondimento dedicato al trasferimento orbitale di un satellite, alla quale si rimanda per una trattazione più approfondita dell'argomento.

 

QUI il quiz del quale questo articolo costituisce la soluzione

Le leggi di Keplero, e non solo, ci dicono che un oggetto in orbita circolare attorno a una massa M ha una velocità maggiore a distanze minori e viceversa. E’ facile ricavare questa conclusione dal calcolo della velocità orbitale che è inversamente proporzionale al raggio (come abbiamo già visto varie volte e rivedremo ancora). Tuttavia, se volessi trasferire il satellite su un orbita più ampia dovrei aumentare il raggio e per far ciò dovrei accelerarlo. Sembrerebbe un controsenso: per portare un satellite su un’orbita più lontana, dove ha una velocità orbitale minore, sono costretto ad accelerarlo, ossia ad aumentare la sua velocità…

Ovviamente, la confusione nasce solo da una scarsa conoscenza della dinamica planetaria

Non è certo la velocità a controllare il moto orbitale, ma è l’energia totale del sistema. Il cambiamento dell’energia dovuto al cambiamento dell’orbita determina la velocità finale. In altre parole, per cambiare orbita devo regalare energia in modo più o meno istantaneo e poco importa l’accelerazione che viene impartita al satellite durante il periodo del trasferimento attraverso una forza più o meno impulsiva. Raggiunta l’altezza necessaria, la forza aggiuntiva si azzera ed è solo la nuova energia raggiunta che regola il movimento del satellite. Da un punto di vista teorico tutto si riduce al calcolo dell’energia necessaria. Da un punto di vista pratico le cose devono essere fatte al momento giusto e nel modo giusto e questo ci permette di introdurre una tipica manovra, quella detta di Hohmann.

Andiamo quindi con calma e prima risolviamo il semplicissimo problema dell’energia necessaria a spostarsi su un orbita più larga.

Regaliamo energia teorica

Il nostro satellite si trova immerso in un campo gravitazionale (conosciamo ormai bene come lavora), ma si sta anche muovendo con una certa velocità V. Ne segue che l' energia totale è composta da due termini: energia cinetica legata alla velocità e energia potenziale legata alla sua posizione rispetto alla massa M della Terra. Non dobbiamo fare altro che scrivere queste due energie e sommarle in modo da avere l’energia totale in una certa orbita.

Per trovare l’energia cinetica è necessario calcolare immediatamente la velocità del satellite. Per farlo basta ricordare che la forza centripeta è in questo caso la forza gravitazionale. In altre parole (come abbiamo già ripetuto spesso e volentieri), il satellite nel suo sistema di riferimento deve imporre l’uguaglianza tra forza gravitazionale (centripeta) e forza centrifuga (deve sentirsi FERMO nel suo sistema).

Basta perciò scrivere la solita formula:

F_C = F_G

mV²/r = GmM/r²        …. (1)

La forza centrifuga deriva dai principi della dinamica che  impongono F = ma, la forza gravitazionale dalla legge di Newton. Ormai queste sono concetti che NOI abbiamo sviluppato parecchie volte e in “molte salse”.

Dalla (1) otteniamo subito la velocità orbitale che è costante nel caso di orbita circolare:

V = (GM/r)^1/2

Da cui l’energia cinetica:

E_C =  ½ m V² = ½ GmM/r

L’energia potenziale dipende solo dall’altezza rispetto alla massa M (a parte m) e vale:

E_P = - GmM/r

Il valore meno deriva dal fatto che l’energia potenziale è sempre negativa e diventa zero (ossia è massima) solo all’infinito. Ma ne abbiamo parlato spesso sia in vari articoli che nel libro della fisica addormentata.

L’energia totale è quindi:

E = E_C + E_P = ½ GmM/r - GmM/r = - ½ GmM/r       …. (2)

Stiamo lavorando in un campo gravitazionale ed è ovvio che alla fine l’energia totale debba dipendere solo e soltanto dalla distanza dal centro (a parte la massa m ).

Non vi sarà certo sfuggito un richiamo fortissimo al teorema del viriale (a cui abbiamo dedicato almeno un articolo) e il risultato veramente banale e intuitivo. L’energia è sempre negativa dato che il satellite è immesso in orbita circolare (sarebbe negativa anche per qualsiasi curva chiusa e quindi ellittica). Essa diventa zero solo se uguagliamo energia cinetica ed energia potenziale. In tal modo ricaveremmo subito una certa velocità, detta di fuga, che è legata all’orbita degenere che corrisponde al caso di energia uguale a zero: la parabola. Se, infine, l’energia diventa positiva, ossia vince l’energia cinetica, siamo di fronte a traiettorie iperboliche (come quelle che hanno gli asteroidi durante un passaggio ravvicinato a un pianeta, effettuato a grande velocità).

Bando alle “ciance” e torniamo al nostro problemino (vedete come la fisica è peggio delle noccioline? Un concetto tira l’altro…).

Per essere più corretti, scriviamo la (2) con i dati del nostro quiz. La Terra ha un certo raggio R e l’altezza orbitale d1 è misurata dalla superficie. Ne deriva:

E₁ = - ½ GmM/(R + d₁)

Cosa vogliamo ottenere a questo punto? Solo e soltanto che l’orbita circolare si effettui a una distanza d₂ = 2d₁ dalla superficie terrestre. L’energia totale legata a questa nuova configurazione non è altro che:

E₂ = - ½ GmM/(R + d₂) = - ½ GmM/(R + 2d₁)

Sembra proprio di aver scritto una banalità. E così è, infatti. La confusione che si fa spesso è del tutto assurda. Tuttavia, in queste formulette così “ridicole”  sonnecchiano all’interno concetti fondamentali come la conservazione dell’energia, il guadagno di energia potenziale a discapito dell’energia cinetica (se vado più lontano, devo viaggiare più lento), ossia le celebri “montagne russe”. Per non parlare di momento angolare… Spostare un oggetto su un’orbita superiore vuol dire cambiargli il momento angolare (NON si conserva, dato che vi è una forza impulsiva esterna). Ma il momento angolare è legato alla distanza dal centro e quindi il satellite guadagna momento angolare.

Ci sarebbe da parlare di ore di meccanica classica e di come la forza esterna deve essere impartita. Pensateci, ma non pretendete che vada avanti in questo discorso… Ci sono troppe cose in gestazione. Ma, sicuramente ci torneremo, descrivendo il moto effettivo di un corpo soggetto alla forza gravitazionale nel caso più generale. Ormai conosciamo le derivate e tra non molto anche gli integrali e quindi…

Torniamo al nostro quiz e risolviamolo velocemente. Abbiamo calcolato l’energia totale iniziale e quella totale finale (entrambe minori di zero, essendo su orbite circolari). Qual è l’energia che dobbiamo impartire al satellite per eseguire il trasferimento di orbita? Veramente banale: la differenza tra le due energie!

ΔE₁₂ = - ½ GmM/(R + 2d₁) + ½ GmM/(R + d₁)

ΔE₁₂  =  GmMd₁/(2(R + 2d₁)(R + d1))

Com’è facile calcolare l’energia da regalare al nostro satellite per farlo rivolvere su un’orbita più alta! Da un punto di vista teorico abbiamo ragione. Da un punto di vista pratico le cose si complicano abbastanza, dato che dobbiamo effettivamente impartire delle velocità al satellite (non per altro si parla di ΔV nelle manovre orbitali) per poterlo muovere nello spazio (sono proprio loro che determinano uno spostamento in funzione del tempo). Si deve, perciò, agire in momenti particolari e con valori particolari, per potere ottenere alla fine proprio la differenza di energia necessaria.

Accenniamo solo a uno di questi sistemi, il trasferimento alla Hohmann, (in modo estremamente empirico… Lampo mi perdoni!)

Regaliamo energia in modo pratico

Abbiamo visto che ad ogni orbita corrisponde una certa energia e, di conseguenza, una certa velocità del satellite, in accordo con la legge del moto. Più in generale, se l’orbita fosse ellittica, la velocità cambierebbe da punto a punto, raggiungendo il valore massimo al perigeo e il valore minimo all’apogeo. Problemi? Direi proprio di no. Al perigeo il satellite è più vicino alla Terra e quindi va più veloce; all’apogeo è più lontano e quindi va più lento. Tuttavia, l’energia orbitale è quella che è: ogni orbita ha la sua energia.

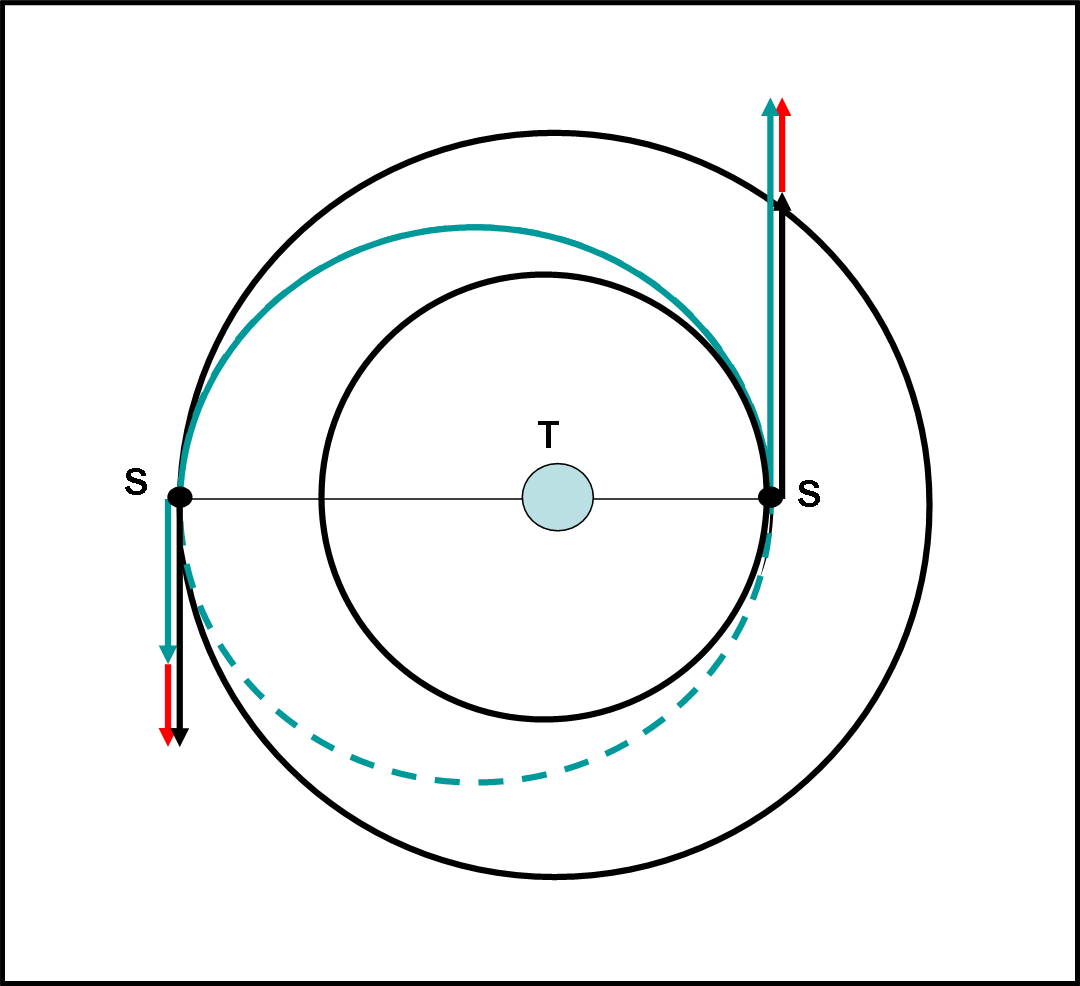
Il regalo di energia va quindi dato al momento giusto e nel modo giusto, agendo su ciò che è ottenibile con i motori, ossia una variazione di velocità. Seguiamo in modo semplificato ciò che si deve fare, utilizzando la figura che segue…

 

Il satellite rivolve sull’orbita nera interna con una certa velocità nera. Agiamo, impartendo una certa velocità attraverso i razzi, indicata dalla freccia rossa. Otteniamo una velocità azzurra. Essa è esattamente la velocità che ha il satellite quando si trova al perigeo dell’orbita ellittica azzurra. Esso descrive allora quest’ellisse fino a giungere all’apogeo con una velocità decisamente più bassa. Impartiamogli allora una seconda velocità rossa in modo da fargli ottenere la velocità che avrebbe un satellite posto in quella posizione in moto circolare attorno alla Terra. A questo punto il satellite si muove con la freccia nera esterna e descrive un’orbita circolare esterna. Notiamo che quest’ultima velocità è minore di quella che aveva sull’orbita iniziale. Giocando con le velocità al perigeo e all’apogeo di un orbita ellittica di trasferimento siamo riusciti a ottenere una velocità minore di quella iniziale pur impartendo sempre impulsi di velocità positivi nei posti giusti e al momento giusto.

Si è dimostrato perfettamente che dare velocità a un satellite,  per farlo salire e viaggiare a velocità più bassa, NON è assolutamente un’assurdità. Tutto il gioco sta sull’energia finale e sul metodo usato per ottenerla. Ottenuta l’energia necessaria, la velocità ne è una conseguenza. In fondo è sempre la stessa storia: si perde in energia cinetica e si guadagna in energia potenziale.

Ovviamente, dato che la fisica non è opinione, parlare di energia acquisita o ceduta si traduce immediatamente in acquisto o perdita di momento angolare a seguito del cambiamento delle condizioni. La forza che è stata impartita non passa per il centro di rotazione e quindi ha regalato momento angolare con le ovvie conseguenze su velocità di rivoluzione (tutto torna sempre). Ben diversa sarebbe la soluzione se la forza impartita fosse in senso opposto al centro. Il momento angolare dovrebbe mantenersi anche se l’orbita sarebbe costretta a cambiare forma. Nessun problema, dato che l’energia orbitale dipende dal semiasse, ecc., ecc., ecc. Ma questo è tutto un altro discorso da fare con molta calma.

Fermiamoci qui per riflettere un poco e la prossima volta applicheremo il tutto all’anello f, ai suoi pastori e parleremo della loro ipotetica origine.

 

QUI trovate la domanda del quiz

QUI trovate l’articolo che spiega il meccanismo di sopravvivenza e l’ipotesi di formazione dell’anello f di Saturno