Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

 

Questo articolo è dedicato alla velocità orbitale di un oggetto nel caso generale dell’ellisse. Lo lascio un po’ in evidenza e poi lo vado a inserire negli approfondimenti, come appendice del moto dei due corpi, di cui utilizza varie relazioni. I richiami che troviamo nel testo si riferiscono a quell’articolo (QUI)

La velocità orbitale v è sempre tangente all’orbita, per cui può essere scomposta in due componenti: la prima v_R diretta come il raggio vettore r e l’altra lungo la sua normale v_N.

Utilizziamo la Fig. 1, per tutta la trattazione.

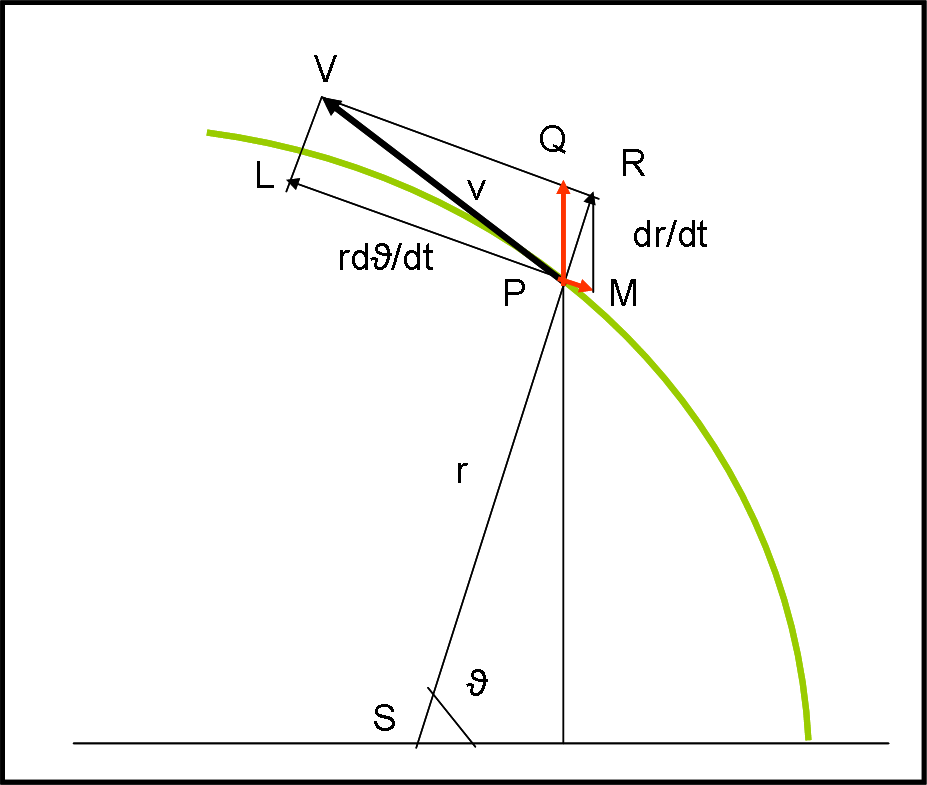
Le due componenti sono date dalla variazione del raggio vettore e della sua perpendicolare rispetto al tempo. Ossia:

v_R = dr/dt

v_N = ds/dt = rdϑ/dt

da cui

v² = (dr/dt)² + r²(dϑ/dt)²

Ovviamente, se l’orbita fosse circolare  dr/dt = 0 e v_C = 2πr/P

Cerchiamo di ricavare v_R …

Nella trattazione delle leggi di Keplero, a partire dalla legge di Newton, abbiamo ottenuto la relazione (42) che porta alla descrizione dell’orbita:

u = (μ/h²)(1 + e cos ϑ )            …. (1)

dove

u = 1/r

h  = r²dϑ/dt    (la costante della velocità areolare)        …. (2)

μ = G(M + m)

Deriviamo la (1) rispetto all’angolo ϑ:

du/dϑ = - (μ/h²) e sen ϑ

Tuttavia, poco prima della relazione (40), avevamo ottenuto:

dr/dt = - h du/dϑ

e, quindi:

dr/dt = (μ/h) e sen ϑ          …. (3)

Dalla (2)

h  = r²dϑ/dt

h = r r dϑ/dt

ma 1/r = u

h u =  r dϑ/dt

e sostituendo la (1)

r dϑ/dt = (μ/h)(1 + e cos ϑ )      …. (4)

La (3) e la (4) ci regalano le due componenti della velocità. Per ottenere il valore di v², basta quadrare e sommare la (3) e la (4):

v² = (μ/h)² e² sen²ϑ + (μ/h)²(1 + e cos ϑ )²

ricordando che  (sen²ϑ + cos²ϑ) = 1

v² = (μ/h)² (e² + 1 + 2e cos ϑ)               (scrivendo 2 - 1 al posto di 1)

v² = (μ/h)²(2 - (1 - e²) + 2e cos ϑ )

v² = 2μ (μ/h²)(1 + e cos ϑ) - (μ/h)²(1 - e²)

Ricordando la (1) si ha:

v² = 2 μ u - (μ/h)²(1 - e²)

v² = 2 μ/r – μ (μ/h²)(1 - e²)

Ma (subito dopo la (43)), sappiamo che

h²/μ = a(1- e²)    …. (5)

Per cui:

v² = 2 μ/r – μ (1 - e²)/(a(1- e²))

v² = μ (2 /r – 1/a)          …. (6)

 Ovviamente, se r = a (orbita circolare), si ottiene v² = μ/a

A questo punto, possiamo divertirci a trovare i valori estremi della velocità, ossia quelli del perielio e dell’afelio.

Al perielio si ha:

r_P = a(1 – e)

da cui:

v_P² = μ (2/(a –ae) – 1/a) = (μ/a) (2/(1 – e) -1) = (μ/a) (2 - 1 + e)/(1 – e)

v_P² = (μ/a) (1+ e)/(1 – e)

All’afelio si ha:

r_A = a(1 + e)

da cui:

v_A² = μ (2/(a + ae) – 1/a) = (μ/a) (2 - 1 – e)/(1 + e)

 v_A² = (μ/a) (1 – e)/(1 + e)

Moltiplicandole tra di loro si ha un interessante risultato:

v_Pv_A = μ/a

Che ci dice che il prodotto dei moduli delle velocità all’afelio e al perielio è una costante che dipende solo dal semiasse dell’orbita.

Volendo, si può anche scomporre la velocità orbitale secondo due componenti diverse, ossia lungo la normale al raggio vettore (come prima) e lungo la normale all’asse maggiore.

Per fare questo scomponiamo la componente lungo il raggio vettore PR (dr/dt) secondo PQ e PM.

Dal triangolo PRQ (con QPR = 90 – ϑ)

PR = PQ cos (90 – ϑ) = PQ sen ϑ

PQ = PR/sen ϑ

E dal triangolo PMR:

PM = PR tan (90 – ϑ) = PR cos ϑ /sen ϑ

PR non è altro che dr/dt e quindi:

PQ = (dr/dt)/sen ϑ

PM = (dr/dt) cos ϑ /sen ϑ

Dalla (3) si ha:

dr/dt = (μ/h) e sen ϑ

sostituendo:

PQ = (μ/h) (e sen ϑ/sen ϑ) = μe/h

PM = (μ/h) (e sen ϑ cos ϑ)/sen ϑ = (μ/h) e cos ϑ

PQ è proprio la componente della velocità secondo la perpendicolare al semiasse maggiore, mentre, per avere quella lungo la normale al raggio vettore, dobbiamo sottrarre PM a LP =  rdϑ/dt

LP – PM = rdϑ/dt - (μ/h) e cos ϑ

Ma la  (4) ci dice che:

r dϑ/dt = (μ/h)(1 + e cos ϑ )

Sostituendo:

LP – PM = (μ/h)(1 + e cos ϑ ) - (μ/h) e cos ϑ = μ/h

Chiamiamo quest’ultima componente v_N, mentre chiamiamo v_Na quella definita da PQ.

Le due componenti della velocità sono, perciò:

v_N = μ/h

v_Na = μe/h

In altre parole, la velocità di un pianeta, in qualsiasi punto della sua orbita, può considerarsi composta da due componenti di modulo costante, una sempre perpendicolare al semiasse maggiore (costante anche come direzione) e una perpendicolare alla direzione istantanea del raggio vettore.

Possiamo anche scriverle in modo più … diretto e comprensibile.

Ricordiamo, infatti, che h è il doppio della costante della velocità areolare. Il che vuol dire che  deve rimanere costante anche se l’area descritta è tutta l’ellisse, ossia (doppio dell’area dell’ellisse diviso il tempo):

h = 2πab/P

e, dalla terza di legge di Keplero, che:

μ = G (M + m) = 4π²a³/P²

μ/h = (4π²a³/P²)/(2πab/P) = 4π²a³ P/(2πabP²) = 2πa²/Pb = 2πa²/(Pa(1 – e²)^1/2)

μ/h = 2πa/(P(1 – e²)^1/2)

E, in conclusione:

v_N = 2πa/(P(1 – e²)^1/2)

v_Na = 2πae/(P(1 – e²)^1/2)

In poche parole, conoscendo semiasse ed eccentricità (geometria orbitale) si hanno subito le componenti costanti delle velocità (in modulo). Ed è interessante notare che le due differiscono solo per l’eccentricità… Il corpo si muove con una velocità di modulo costante che è sempre normale al raggio vettore (come fosse una specie di moto circolare), ma a questa deve aggiungersi una componente più o meno grande a seconda dell’eccentricità orbitale.