Categorie: Matematica
Tags: Proprietà integrali definiti teorema della media
Scritto da: Vincenzo Zappalà
Commenti:6
44. Le proprietà degli integrali definiti *
Quanto descritto in questo articolo può sembrare di una banalità quasi ridicola. Tuttavia, definisce alcune proprietà degli integrali definiti che diventano importantissime nel calcolo vero e proprio degli integrali. E’ nostro dovere affrontarle e dimostrarle con la giusta serietà.
Vogliamo continuare a trattare i vari concetti in modo elementare per poter permettere a tutti di seguire e comprendere appieno le proprietà degli integrali definiti appena introdotti. Proprietà che potrebbero essere dimostrate in modo molto formale, ricordando che gli integrali definiti non sono altro che limiti di sommatorie. Tuttavia, sappiamo anche che gli integrali definiti non sono altro che le aree racchiuse tra una certa funzione e l’asse delle x, in un certo intervallo dell’ascissa e, quindi, sfruttiamo questo concetto di facilissima comprensione per dedurre le proprietà più importanti.
A molti sembreranno discorsi veramente banali e addirittura inutili. Non facciamoci ingannare da ciò che sembra così facile: le proprietà degli integrali saranno fondamentali per poter risolvere casi ben più complessi. Ne segue che riuscire a dimostrale, anche in modo semplificato e apparentemente empirico, è una necessità fondamentale per sapere con chi abbiamo a che fare. Non ridete, perciò, se vi proporrò figure e descrizioni veramente… ridicole!
Cominciamo con quella che è forse la proprietà più “difficile”:
∫ab [f(x) + g(x)]dx = ∫ab f(x) dx + ∫ab g(x) dx …. (1)
Essa dice che l’integrale della somma di due funzioni è uguale alla somma degli integrali delle due funzioni.
Quanto detto lo possiamo raffigurare nella Fig. 1
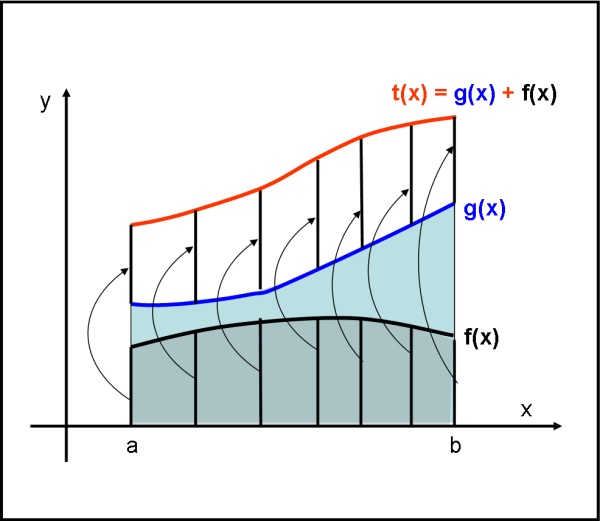
La funzione f(x) sia la curva nera e la funzione g(x) quella blu. Entrambe vanno considerate nell’intervallo (a,b). Sappiamo molto bene che l’integrale della funzione f(x) non è altro che l’area racchiusa tra la curva nera e l’asse delle x. Analogamente l’integrale della funzione g(x) non è altro che l’area racchiusa tra la curva blu e l’asse delle x.
Cosa vuol dire costruire una nuova funzione t(x) che sia somma di due funzioni? Banale, veramente banale… Basta sommare per ogni x le corrispondenti y. Ossia effettuare la somma f(x) + g(x). Non è certo difficile raffigurarla nella Fig. 1. Per ogni punto della curva blu aggiungiamo alla sua ordinata l’ordinata relativa alla curva nera. La somma delle due ordinate identifica un punto della funzione t(x), somma delle due funzioni, che è rappresentata dalla curva rossa.
Abbiamo solo eseguito una somma…
t(x) = g(x) + f(x)
L’integrale di questa nuova curva non è altro che l’integrale della somma delle due funzioni di partenza, ossia il primo membro della relazione (1).
La relazione (1) ci dice che questa area deve essere uguale all’area della curva nera sommata all’area della curva blu. Ma la curva blu è quella che è, e allora ciò che si deve provare è che l’area compresa tra la curva rossa e quella blu deve essere uguale all’area della curva nera.
Dimostriamolo lavorando con aree che sappiamo calcolare immediatamente. Ciò che vale per funzioni semplici deve valere anche per funzioni più complicate. L’integrale è stato definito in modo generale e quindi non fa alcuna differenza tra le funzioni utilizzate.
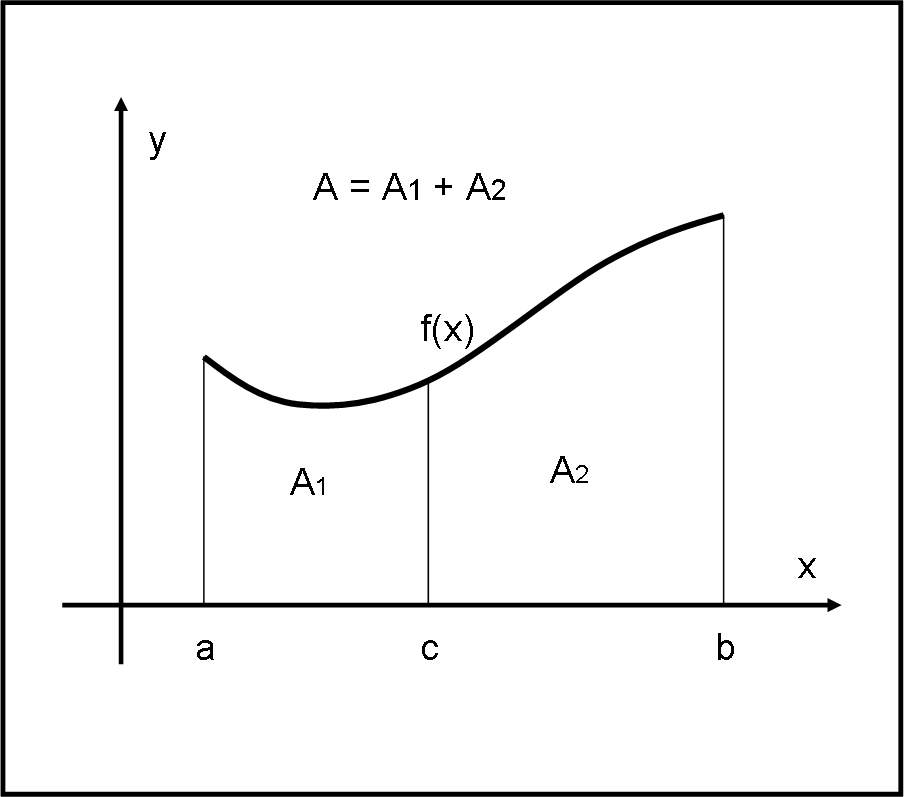
Consideriamo la Fig. 2.

Le due funzioni sono adesso due belle rette, scelte con una certa furbizia. La prima (quella nera) ha equazione:
f(x) = - mx + n
La seconda (quella blu) ha equazione:
g(x) = mx + n
Costruiamo, come prima, la funzione t(x) definita come somma di f(x) e di g(x). Lo possiamo fare sia graficamente che analiticamente:
t(x) = f(x) + g(x) = - mx + n + mx + n = 2n
La funzione somma non è altro che la retta orizzontale di equazione
y = t(x) = 2n
L’area di questa funzione è calcolabile immediatamente dato che è quella di un rettangolo di lati 2n e (b – a). Essa vale:
2n(b-a)
Che, ovviamente, non è altro che l’integrale della funzione somma, tra a e b, ossia:
∫ab [f(x) + g(x)]dx = 2n(b-a) …. (2)
Calcoliamo adesso, separatamente, le aree delle due funzioni di partenza. L’area di f(x) (curva nera) non è altro che l’area di un triangolo di lati n e (b-a), ossia:
∫ab f(x) dx = n(b - a)/2
L’area di g(x) (curva blu) è l’area del trapezio che per basi n e 2n e per altezza (b-a), ossia:
∫ab g(x) dx = (n + 2n)(b – a)/2
Non ci resta che sommare i due integrali e abbiamo:
∫ab f(x) dx + ∫ab g(x) dx = n(b - a)/2 + (n + 2n)(b – a)/2 = (nb – na + nb – na + 2nb – 2na)/2
∫ab f(x) dx + ∫ab g(x) dx = (2nb – 2na + 2nb – 2na)/2 = 4(nb – na)/2 = 2n(b-a)
Il risultato trovato è esattamente quello della (2) e, quindi, possiamo concludere che:
∫ab [f(x) + g(x)]dx = ∫ab f(x) dx + ∫ab g(x) dx
Che non è altro che la (1). La proprietà è dimostrata.
Ovviamente, si poteva ottenere la stessa conclusione guardando solo la figura 2. Al trapezio blu aggiungiamo il triangolo e otteniamo l’area della somma delle due funzioni (ossia il rettangolo rosso). Ma il triangolo compreso tra la retta rossa e quella blu è uguale al triangolo nero, da cui segue che l’area del rettangolo rosso è uguale alla somma dell’area del trapezio blu e quella del triangolo nero. Sostituendo alla parola area la parola integrale abbiamo proprio la proprietà (1).
Sì, lo ammetto, ho scritto tanto per dimostrare una cosa che sembra proprio immediata. La dimostrazione formale è, forse, molto più breve… ma non così semplice. Fidatevi, anche se questa lunga disquisizione non la trovate in giro per la rete…
Fortunatamente, le altre proprietà si dimostrano più rapidamente…
Passiamo alla seconda:
∫ab f(x) dx = ∫ac f(x) dx + ∫cb f(x) dx …. (3)
Essa dice che data un funzione f(x), il suo integrale tra a e b si può spezzare in due integrali tra a e c e c e b, sempre che c sia compresa tra a e b. Proprietà questa di estrema importanza nel calcolo di aree molto complicate e di integrali molto scorbutici.
Se traduciamo la frase precedente utilizzando le aree, la proprietà si dimostra immediatamente, come mostra la Fig. 3. L’area totale A è ovviamente uguale alla somma delle aree A1 e A2.
Passiamo alla terza:
∫ab k f(x) dx = k ∫ab f(x) dx …. (4)
Beh…, per dimostrare la (4) non c’è nemmeno bisogno di fare delle figure… basta ricordare la (1).
La (4) si può scrivere:
∫ab k f(x) dx = ∫ab [f(x) + f(x) + f(x) + … + f(x)]dx (abbiamo sommato f(x) k volte)
Per la (1), però, si può anche scrivere:
∫ab [f(x) + f(x) + f(x) + … + f(x)]dx = ∫ab f(x) dx + ∫ab f(x) dx + …. + ∫ab f(x) dx = k ∫ab f(x) dx
La (4) è dimostrata.
La prossima è veramente ridicola e la scriviamo soltanto:
∫aa f(x) dx = 0 …. (5)
Se non facciamo muovere la x è ovvio che l’area rimane uguale a zero, qualsiasi sia la funzione: y moltiplicata per zero deve dare zero.
La banalissima (5) è importante perché ci permette di dimostrare la proprietà seguente:
∫ab f(x) dx = - ∫ba f(x) dx …. (6)
Dal punto di vista geometrico non sarebbe immediata, a meno di considerare le x negative, dato che si parte da destra e si va verso sinistra, nell’intervallo (a,b). Molto meglio fare due calcoli semplici semplici.
0 = ∫aa f(x) dx = ∫ab f(x) dx + ∫ba f(x) dx (proprietà (3))
E, quindi:
∫ab f(x) dx = - ∫ba f(x) dx
Non ci rimane che un’ultima proprietà tra quelle più utili e importanti, che prende il nome di teorema della media e che richiama (in qualche modo) quanto avevamo trovato nella Fig. 5 del capitolo 40: l’area del triangolo è uguale all’area di un rettangolo che ha per base la stessa base e per altezza la metà dell’altezza. Nel caso attuale, possiamo generalizzare quel risultato dicendo che data una funzione qualsiasi e il suo integrale in un certo intervallo (a,b), esiste almeno un’ascissa c compresa nell’intervallo (a,b) tale che:
∫ab f(x) dx = f(c)(b – a) …. (7)
La (7), in parole povere, si può “tradurre”: data una certa funzione, esiste sempre un rettangolo di base (b – a) e altezza f(c), con c compresa tra a e b, tale che la sua area sia quella della funzione nell’intervallo (b - a).
La dimostrazione esiste e non è nemmeno difficile, ma presuppone la conoscenza di altri tre teoremi. Direi che ne possiamo fare a meno e fare un ragionamento abbastanza logico e immediato, utilizzando la Fig. 4.
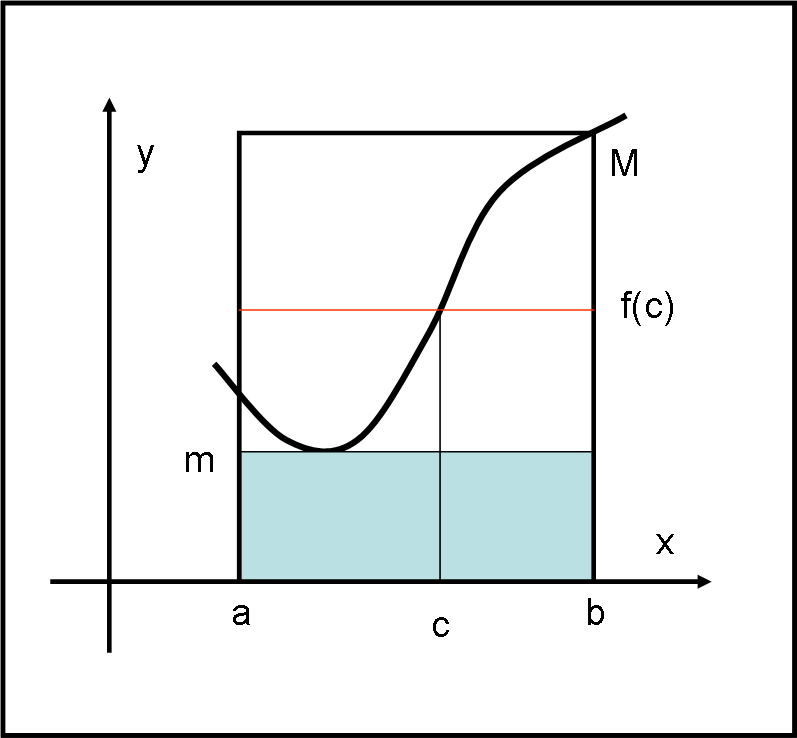
Se la funzione f(x) è continua nell’intervallo (a,b) deve esistere un suo punto di minimo e uno di massimo assoluto, ossia un punto in cui la f(x) è minima e un punto in cui f(x) è massima (poco a che vedere con i massimi e minimi dello studio delle funzioni, anche se possono coincidere). Notate che il minimo è il massimo possono essere sia punti estremi che intermedi, poco importa. Costruiamo il rettangolo azzurro e quello bianco che abbiano come lato verticale il valore minimo m della f(x) e il valore massimo M della f(x).
L’integrale di f(x), ossia l’area della funzione nell’intervallo (a,b), sarà ovviamente compresa tra le aree dei due rettangoli. Ossia:
m (b – a) < ∫ab f(x) dx < M(b – a)
E, ancora:
m < ∫ab f(x) dx/(b – a) < M
∫ab f(x) dx/(b – a) è un numero compreso tra i due numeri che rappresentano gli estremi della funzione. Ma, se la funzione è continua, deve assumere tutti i valori intermedi tra m e M. Deve perciò sicuramente esistere un’ascissa c, intermedia tra a e b, tale che f (c) sia proprio il numero cercato. Ossia:
∫ab f(x) dx/(b – a) = f(c)
E, quindi, la (7) è dimostrata.
Bene, siamo quasi pronti a introdurre (e dimostrare) il teorema fondamentale del calcolo integrale. Prima, però, ci dedicheremo brevemente alle aree "negative" e al calcolo di aree comprese tra curve qualsiasi.
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






6 commenti
Caro Enzo, ho una domanda sull'ultima proprietà.... ossia f(c) è sicuramente compresa tra m e M, ma non è detto che l'ordinata di f(c) sia proprio in mezzo tra m e M, come nel caso trattato nel capitolo 40 (figura 5), oppure no?
Paolo
No, ovviamente no, caro Paolo. Lo è solo per la retta... Purtroppo ho fatto una figura che dà quell'idea, ma prova a cambiare la forma e vedrai che c si muove... lascia gli stessi estremi e cambia la funzione. L'area cambia, ma (b-a) rimane lo stesso e, quindi, deve cambiare f(c). Tra parentesi non ho calcolato l'area e quindi ho preso un c a casaccio...
Grazie mille Enzo... .trasformare la figura era proprio ciò che avevo fatto mentalmente, da qui sorgeva la domanda.
.trasformare la figura era proprio ciò che avevo fatto mentalmente, da qui sorgeva la domanda.
Paolo
Paolo,
f (c) è un'ordinata, forse per "ordinata di f (c)" intendevi l'ascissa di f (c), e cioè proprio c.
Quello che Enzo sfrutta è un teoremino che afferma: se hai il minimo m e il massimo M (anch'essi ordinate, si trovano sull'asse y), allora f (c) è sicuramente compreso tra m e M. Ciò non vale se ti riferisci all'asse x! Cioè, supponi che:
m = f (x1) e M = f (x2)
e cioè considerando le ascisse dei punti di minimo e massimo, allora non è assolutamente detto che c sia compreso tra x1 e x2!
Naturalmente questo discorso vale solo se parliamo di funzioni continue.
caro Giuseppe,
penso che Paolo intendesse proprio la giusta denominazione... un errore di sbaglio...
Intendevo proprio dire che nella figura 4, f(c) è tra m ed M, usando l’asse delle ordinate come riferimento e non quello delle ascisse.
Ho solo indicato f(c) m ed M come se fossero dei punti nella figura 4, dopodiché Giuseppe hai sicuramente ragione a dire che f(c) è una funzione per cui è già un’ordinata.
Paolo