Categorie: Astronomia Elementare Fenomeni astronomici
Tags: Aristarco astronomi greci distanza pianeti Keplero periodo pianeti secoli bui storia astronomia terza legge Keplero
Scritto da: Vincenzo Zappalà
Commenti:2
Aristarco e la terza legge di Keplero **
Questo articolo è stato inserito nella sezione d'archivio "Astronomia classica" e in "Antichi Greci, che passione!"
In attesa di avere qualche risposta sul quiz servito come “aperitivo” (l’estate è ancora lunga), permettetemi di presentare una visione apparentemente fantascientifica delle possibili conseguenze delle geniali idee di Aristarco. Più ci si pensa, però, e più sembra quasi ovvio che Aristarco avrebbe potuto cambiare la storia della Scienza, se solo avesse avuto un certo tipo di appoggi politici. Probabilmente, avrebbe potuto (e magari l’ha anche fatto) anticipare la terza legge di Keplero.
Lo scopo di questa parte più “fantascientica” dell’articolo sui grandi astronomi greci, è quello di far comprendere al meglio l’intuizione geniale di Aristarco sul moto parallattico delle stelle fisse.
Ripetiamo il concetto, in modo molto semplificato. Se la Terra gira intorno al Sole, si deve spostare nello spazio di una quantità pari al diametro della sua orbita supposta circolare, nel giro di un anno. Se le stelle sono fisse, il moto della Terra viene attribuito alle stelle, che descrivono delle ellissi apparenti nel cielo (rispetto a oggetti molto più distanti) (QUI). L’ampiezza di queste è legata direttamente alla distanza della stella. Più è grande l’ellissi e più vicina è la stella.
Ai tempi di Aristarco, gli strumenti non permettevano di identificare queste ellissi nemmeno per le stelle più vicine. La sua conclusione fu, quindi, di assumere che le stelle fossero decisamente lontane. Un grande vantaggio per stabilire esattamente il moto dei pianeti…
D’altra parte, però, senza ellissi, cadeva la prova del movimento della Terra attorno al Sole. Questo, almeno, era più che sufficiente per i detrattori della teoria eliocentrica.
Aristarco continuò sicuramente a essere convinto della sua ipotesi e si dedicò, sicuramente, a una prova ben più facile da osservare: i pianeti. Il loro moto, inoltre, aveva come sfondo delle stelle VERAMENTE fisse (come aveva dimostrato) e quindi perfette come punti di riferimento immobili.
Immaginiamo, per un attimo, che un pianeta sia fermo. Cosa vedrebbe un osservatore terrestre? Esattamente quello che Aristarco cercava nelle stelle fisse, ossia un’ellissi apparente nel moto del pianeta. In fondo, un pianeta fermo non è altro che una stella fissa molto vicina. Sotto queste ipotesi, sarebbe stato facile per Aristarco misurare la distanza del pianeta, come oggi vengono misurate le distanze delle stelle vicine. Una misura non assoluta, ma relativa alla distanza Terra-Sole.
Purtroppo, anche i pianeti girano intorno al Sole. Inoltre più sono vicini e più girano in fretta. Ciò comporta una sovrapposizione di moti: quello proprio del pianeta attorno al Sole e quello apparente dovuto al movimento della Terra.
In poche parole, l’ellissi parallattica non si chiude mai e causa una traiettoria apparente fatta da “nodi” che sono intervallati da periodi più o meno lunghi di andamento più o meno costante.
Più il pianeta è lontano e più è facile vedere questa combinazione di moti. Prendiamo Plutone (che purtroppo Aristarco non conosceva). Il suo periodo di rivoluzione è così lungo che può essere considerato una stella “quasi” fissa. La Fig. 1 mostra il moto apparente di Plutone visto dalla Terra: un insieme di ellissi che si spostano lentamente una rispetto all’altra in base al movimento vero di Plutone attorno al Sole.
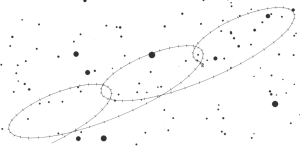
Se il pianeta fosse, invece, molto veloce l’ellisse si deformerebbe in un “cappio” sempre più piccolo, che potrebbe anche scomparire: si noterebbe solo una variazione della sua apparente velocità rispetto alle stelle fisse.
Non è difficile costruire il moto apparente di un pianeta, assumendo una sua velocità intrinseca v0 costante. Partendo da un pianeta fisso (e quindi da un’ellissi chiusa e perfetta), basta aggiungere, a tempi successivi, lo spazio percorso s dato dalla ben nota formula:
s = v0t
Vediamo due casi nella Fig. 2, eseguita in modo molto rozzo, ma sufficiente per la comprensione della combinazione dei moti. In alto la velocità orbitale del pianeta è molto bassa, in basso è decisamente più alta.

Anche a quei tempi, non era certo difficile stabilire osservativamente i periodi sinodici e quindi ricavare i periodi siderali dei pianeti (QUI), ma Aristarco aveva sicuramente capito che i moti di rivoluzione, eseguiti con velocità diverse, portavano a ellissi parallattiche più o meno larghe e più o meno separate
Il grande scienziato era anche sicuramente capace di separare i due moti che producevano la strana traiettoria. Eliminando la componente propria del pianeta, avrebbe potuto descrivere solo e soltanto l’ellisse parallattica relativa al pianeta, fermo e fisso come una stella molto vicina. Di conseguenza avrebbe avuto in mano sia la distanza che il periodo di rivoluzione dei pianeti…
La conclusione, secondo me, è abbastanza ovvia: bastava creare una piccola tabella tra questi due valori e si sarebbe trovata una strana relazione matematica del tipo:
P2/d3 = costante
Nient’altro che la … terza legge di Keplero!
La fantascienza si dissolve sempre di più e sto pensando a come sarebbe stato il mondo se Aristarco avesse potuto divulgare adeguatamente i suoi calcoli (secondo me li ha fatti sicuramente, avendone i mezzi e, soprattutto, la mente necessaria)… Quando sarebbe nato uno come Newton?
Mi ricordo una frase letta molto tempo fa, riguardante il sommo pittore rinascimentale Masaccio: “Giotto posò il suo pennello che venne raccolto e nuovamente usato da Masaccio”. Così possiamo dire che Aristarco posò il pennello e solo Copernico, Keplero e Galileo l’hanno ripreso in mano. Che enorme BUCO nella storia della Scienza astronomica…
Aristotele è stato uno dei “sommi” pensatori umani, ma non averlo MAI voluto contraddire ha cambiato l’evoluzione scientifica. Diciamo che un po’ mi sta… antipatico, ma sono molto peggio coloro che hanno continuato a imporre le sue idee con la forza, le torture e i roghi. In fondo, in fondo, senza mai aver chiesto perdono all'umanità intera…
La fanta(?)scienza degli antichi Greci continua QUI
Chi è interessato, QUI può trovare un approfondimento sulle leggi di Keplero





2 commenti
Mi piace leggere di storia dell'astronomia, o della scienza in generale, proprio per quello che evidenzia questo articolo.
Rimango sempre colpito dal tempo e dagli sforzi necessari a menti eccelse per avanzare anche di qualche piccolo passo nella conoscenza. Viene spesso il dubbio che ci fossero arrivati prima di quanto ci è noto, ma per qualche ragione la scoperta si fosse persa. Ma quando il periodo storico è bene documentato appare improbabile che ciò sia accaduto.
Allora capisco il mio errore di prospettiva, quello che oggi appare un piccolo passo spesso non lo è affatto. Sono state le intuizioni ed il lavoro di chi a fatto le scoperte e di tutta la comunità scientifica che ha prima creato le condizioni per la scoperta e poi le ha continuamente sistematizzate e rielaborate a renderle oggi accessibili.
Questo mi fa apprezzare ancora di più il lavoro fatto da tutti coloro che hanno contribuito a questo sforzo e l'approccio mentale che ha permesso che questo sforzo si protraesse per secoli e nel medio-lungo termine fosse "cumulativo". Mi viene anche il dubbio che queste condizioni siano una costruzione umana che può facilmente deteriorarsi, come fanno pensare tendenze attuali che mettono sullo stesso piano scienza ed altri approcci di moda.
Nel caso di questo articolo, nel "buco" tra Aristarco e Keplero, metterei Tycho Brahe con le sue raccolte di anni di precise osservazioni sistematiche e continue, i costruttori di strumenti, forse il sistema decimale per i calcoli.
caro Fabrizio,
ricordiamo, comunque, che il grande "buco" non è stata una fase di preparazione... ma di chiusura assoluta. Strumentazione ben poca e Brahe (grandissimo osservatore) è nato a metà '500, proprio dopo la rivoluzione (parziale) copernicana... Quei piccoli passi a cui giustamente fai riferimento potevano essere fatti di corsa se non ci fosse stata la chiusura delle menti (un po' come oggi, ma per altre ragioni...). La trigonometria nasce con Ipparco e il calcolo infinitesimale proviene dagli "infedeli"...
Comunque, sono contento che ti piaccia la storia... vogliamo proprio darle un posto di rilievo