Questo articolo è stato inserito nelle pagine d'archivio "Giove e i suoi tesori", in "Antichi Greci, che passione!"  e in "Parallasse"

Questo articolo lo consiglio vivamente per due motivi essenziali. Innanzitutto, perché mostra come il mistero delle tre eclissi solari di Giove da parte di Callisto sia un’applicazione semplice e perfetta del moto apparente dei pianeti nella volta celeste, niente di meno e niente di più. Inoltre, perché dimostra come gli antichi greci sarebbero stati perfettamente in grado di spiegarlo e prevederlo senza computer e programmi “a scatola chiusa”. In altre parole, chi conosce e ha capito il moto apparente dei pianeti DEVE automaticamente comprendere anche questo “mistero” tutt’altro che misterioso.

Quest’articolo, al di là della problematica astronomica, dovrebbe insegnare a ragionare e a non affidarsi sempre e soltanto alla "tecnologia" tanta scena e poca sostanza. Essa può essere usata per rappresentare qualcosa che abbiamo già capito e risolto, ma non deve essere usata per capire e risolvere ciò che il cervello dei greci (senza telescopi, binocoli, oculari e PC) aveva già saputo descrivere. Ecco perché ho DOVUTO inserire un solo asterisco. Se è stato capito più di duemila anni fa non posso credere che oggi non sia comprensibile a tutti, senza aiuto tecnologico (del tutto inutile a un cervello pensante).

Ho già descritto, in modo molto approssimato e rapido, che il mistero non è un mistero. Adesso, vediamo come la sua soluzione provenga direttamente dallo studio dei moti apparenti dei pianeti sulla sfera celeste. Cominciamo, quindi, proprio da zero e richiamiamo Aristarco di Samo (310 - 230 a.C.). Le sue idee e applicazioni hanno lasciato un segno fondamentale nell’astronomia, ma a noi interessa soprattutto la previsione della parallasse annua, l’inizio di tutto il discorso.

Aristarco credeva che la Terra girasse intorno al Sole. Noi anche e quindi partiamo da ipotesi perfettamente uguali (a parte duemila anni di … evoluzione). Senza alcun programma a scatola chiusa, egli aveva automaticamente pensato di utilizzare il moto della Terra per stabilire, tra le tante cose, la distanza delle stelle. Ovviamente, non poteva, a quei tempi, misurare angoli piccolissimi ed era, quindi, costretto a giungere a conclusioni qualitative, ma, comunque, fondamentali.

Il suo ragionamento deve essere stato questo: “Se la Terra gira intorno al Sole in un anno, noi dovremmo vedere le stelle muoversi nel cielo secondo un piccolo cerchietto o un ellisse o un segmento, a seconda dell’inclinazione orbitale rispetto alla direzione della stella. Noi, infatti ci consideriamo fermi e quindi il moto della Terra lo trasferiamo all’astro che è in realtà immobile. Niente di veramente nuovo, dato che non è altro che il fenomeno della parallasse che vediamo ovunque, in casa e fuori. Ovviamente, più la stella è vicina è più il suo moto apparente è rilevabile. Un metodo perfetto per  misurare le distanze stellari. Purtroppo, nessuna stella che osserviamo nel cielo mostra questo movimento. Cosa possiamo concludere? Che le stelle sono incredibilmente distanti e che, quindi, il loro movimento non è apprezzabile a occhio nudo”. Nessun risultato veramente pratico, ma un’intuizione geniale che ancora oggi si usa per determinare le distanze delle stelle relativamente vicine (vedi, ad esempio, il satellite GAIA dell’ESA).

Per seguire il ragionamento di Aristarco possiamo fare facilmente un paio di figure che TUTTI dovreste conoscere molto bene (astrofili e no). In Fig. 1, sia T la Terra che gira intorno al Sole e che compie una rivoluzione in un anno. Sia P la stella o l’oggetto celeste che preferite. L’importante è che possa considerarsi immobile, almeno in prima approssimazione.

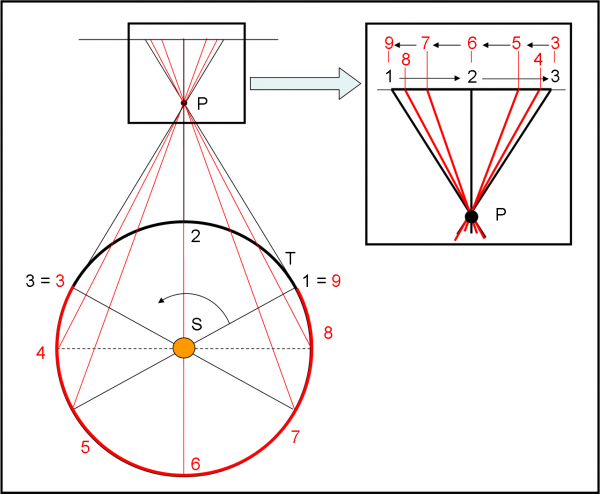
Abbiamo considerato varie posizioni  della Terra l’ungo la sua orbita circolare, separate da angoli uguali e quindi anche da tempi uguali. Ne abbiamo disegnate nove, di cui l’ultima coincidente con la prima, dopo una completa rivoluzione. A seconda della posizione della Terra, l’oggetto P assume una posizione diversa nel cielo rispetto a una direzione fissa (sia questa, ad esempio, la retta verticale).

In questa fase, dato che l’oggetto è talmente distante da poterlo considerare immobile, possiamo tranquillamente considerare la sfera celeste come la linea orizzontale disegnata subito sopra l’oggetto P (parte sinistra della figura). Questa linea la possiamo tracciare alla distanza che vogliamo rispetto a P, dato che quello che osserviamo non è una distanza “lineare”, ma una distanza “angolare” rispetto alla direzione fissa.

Nella parte destra ingrandiamo ciò che vediamo nel cielo, ossia le varie posizioni di P al variare della posizione di T. Si vede bene che il punto P si sposta verso destra da 1 a 3 e poi torna indietro fino a tornare in 1 (posizione 9) dopo un anno esatto.

Qualche considerazione preliminare. L’oggetto P è stato scelto piuttosto vicino (per semplicità di figura) e possiamo notare che, per descrivere l’intero segmento apparente, il punto P impiega molto meno tempo all’andata rispetto al ritorno. Questa differenza diventa sempre meno sensibile al crescere della distanza di P e al diminuire della lunghezza angolare del segmento, come ci mostra la Fig. 2.

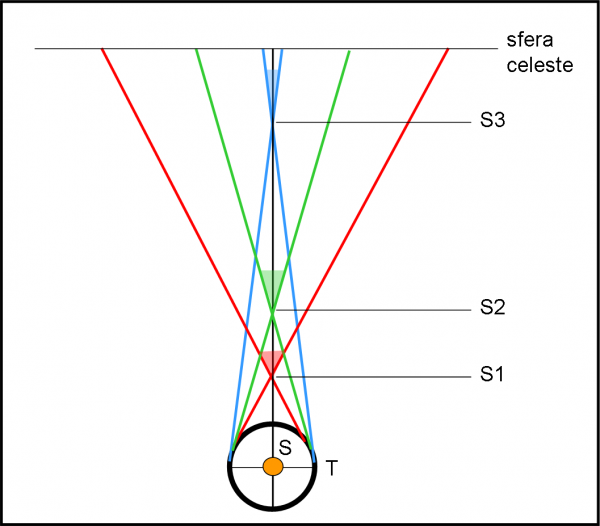
Nelle condizioni delle figure abbiamo scelto l’oggetto P sul piano orbitale della Terra. La parallasse annua si riduce proprio a un segmento descritto prima in un verso e poi nell’altro. Se, però, l’oggetto P non si trova nel piano orbitale della Terra, il segmento si trasforma in un’ellisse come mostrato in Fig. 3. A sinistra, abbiamo la nuova configurazione e, a destra, la trasformazione dal caso complanare (in alto) a quello non complanare (in basso). Questi disegni venivano tracciati senza computer e senza fogli di carta dagli antichi greci e venivano compresi benissimo. Siamo tutti in dovere, perciò, di comprenderli perfettamente con i mezzi (e il cervello) di oggi.

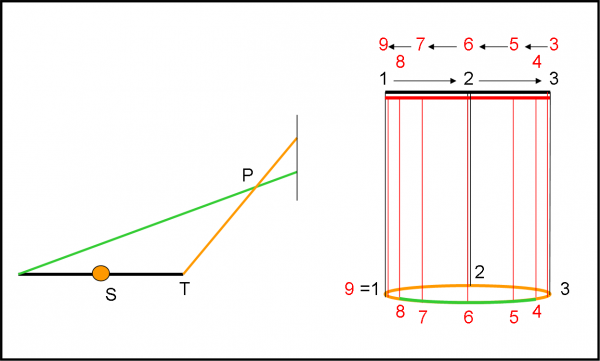
Gli antichi popoli, anche prima dei greci, avevano osservato e descritto come le cose diventavano più complicate se l’oggetto non era più un punto fisso (una stella), ma era anch’esso in movimento. Non avevano moltissimi oggetti a disposizione, soltanto tre (Marte, Giove e Saturno), ma più che sufficienti a capire molte cose e a descriverle con grande perfezione. Una tale perfezione che Ipparco era giù riuscito a introdurre la precessione degli equinozi.

Il succo del discorso non cambia e fa sempre riferimento alla parallasse. Tuttavia, questa volta, la piccola ellisse diventa molto più grande (i pianeti sono molto vicini) e, soprattutto, non può continuare a ripetersi sempre uguale come per le stelle, ma deve tener conto del moto dell’oggetto P.

In poche parole, dobbiamo descrivere il moto apparente dei pianeti (esterni) nel cielo. Una descrizione che era di estrema banalità per gli antichi osservatori del cielo . Non possiamo, quindi, che sperare che sia di dominio pubblico anche oggi, dopo più di duemila anni, soprattutto per coloro che spendono centinaia di euro per comprasi strumentazioni che, in mano agli antichi greci, avrebbero permesso conquiste scientifiche ben più stupefacenti  di quanto non siano riusciti a fare con i soli occhi e qualche sbarra di ferro o poco più.

Purtroppo, anche la spiegazione di ciò che avveniva sarebbe stato altrettanto semplice  per gli antichi se non fosse subentrata l’imposizione di una Terra immobile. Un’imposizione morale e filosofica che gli avrebbe complicato di molto le cose, costringendoli a introdurre gli epicicli e cose del genere. Tuttavia, una spiegazione che doveva essere giocoforza “sbagliata” ci fa ancor meglio comprendere la grandezza della mente umana (almeno di allora…): risolvere il problema del moto apparente dei pianeti in un sistema geocentrico, attraverso l’introduzione degli epicicli, è decisamente una soluzione più complicata di quella relativa a un sistema eliocentrico. Siamo, perciò, decisamente molto fortunati, oggi, che possiamo partire da una configurazione nettamente più facile. Se i greci avevano risolto il problema più difficile, noi possiamo sicuramente fare altrettanto con quello più facile.

D’ora in poi, lavoreremo in modo più “preciso”, riferendoci solo e soltanto a distanze angolari (quelle che si misurano nel cielo) e sintetizzate in Fig. 4. Data una certa posizione della terra T e del pianeta P, consideriamo come distanza tra pianeta e direzione fissa, vista dalla Terra, l’angolo, con vertice nella Terra, segnato in rosso. Tale angolo è identico a quello con vertice nel pianeta.

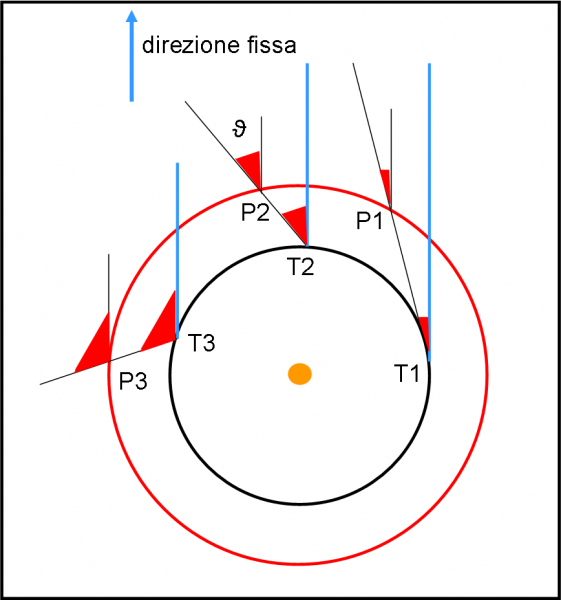
Passiamo, allora, alla “complicatissima” Fig. 5. La Terra descrive l’orbita nera e il pianeta quella rossa. Abbiamo scelto condizioni di partenza particolarmente favorevoli, ma potevamo scegliere qualsiasi configurazione. Teniamo presente che abbiamo impostato periodi orbitali che NON rispecchiano le leggi di Keplero solo e soltanto per avere figure disegnabili su un foglio. Una scelta che non inficia assolutamente il risultato finale in termini di comprensione (anzi lo rende più evidente).

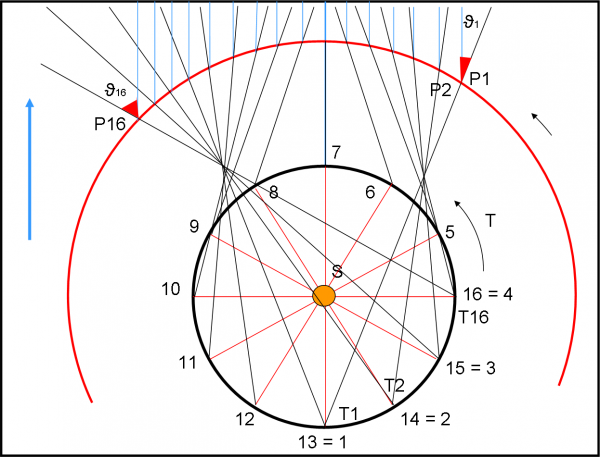
Le due orbite sono circolari e, quindi, i pianeti si muovono di moto circolare uniforme. In altre parole, descrivono archi di cerchio uguali in tempi uguali. In particolare, nel tempo che la Terra passa dalla posizione T1 alla T2, il pianeta passa dalla P1 alla P2, e via dicendo. La direzione del pianeta, istante per istante, è data dalla retta che congiunge Ti con Pi. Notate che tutto sarebbe identico alla parallasse stellare se non fosse che il pianeta di sposta lungo la sua orbita. Non ditemi che la figura è complicata! Ha solo tante rette, ma i concetti sono banali (pensate sempre che lo erano già per i greci e sicuramente anche per chi ha guardato il cielo prima di loro).

La direzione fissa, rispetto a cui misurare gli angoli ϑ (rossi), è sempre quella verticale (blu). Non è certo difficile misurare gli angoli tra la direzione del pianeta e la direzione fissa. Ci accorgiamo che in certi intervalli di tempo questi angoli sono positivi e in altri negativi. In altre parole, per un certo periodo di tempo il pianeta appare andare verso sinistra, poi verso destra, e poi ancora verso sinistra.

Visto che siamo tutti esperti di spazio-tempo, tracciamo una banale figura spazio-temporale che sintetizzi il risultato delle nostre misure. In ascissa mettiamo lo spazio, ma, questa volta, utilizziamo come spazio l’angolo ϑ (in fondo, è una distanza angolare!). L’ordinata è, invece, il solito tempo. Utilizziamo una scala che ci permetta di vedere bene le differenze degli angoli misurati e otteniamo la Fig. 6 di sinistra.

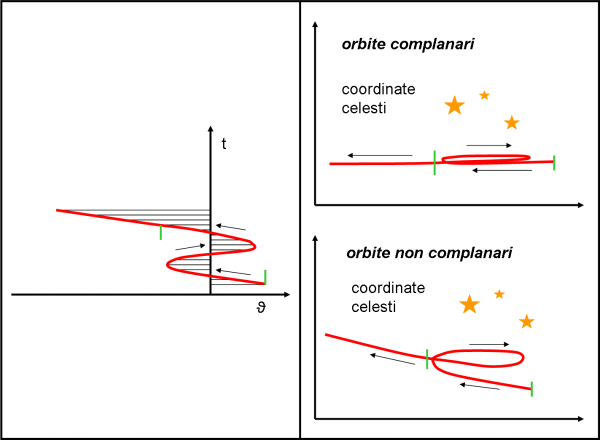
Come già previsto, si ottiene una curva che va verso sinistra, poi si ferma (punto stazionario), e torna indietro fino a un altro punto stazionario, dove inverte nuovamente la direzione di marcia. I due trattini verdi corrispondo al periodo uguale a un anno terrestre. Come si vede molto bene, la “famosa” ellisse parallattica (o “segmento” nel caso complanare) non si chiude e forma il celebre “anello” che i pianeti descrivono nel cielo. Possiamo notare che partendo dall’ipotesi eliocentrica, l’abbiamo ottenuto con estrema facilità. Pensate alla difficoltà di spiegarlo in un sistema geocentrico! Si sono dovuti inventare i celebri epicicli, vera intuizione geniale anche se completamente sbagliata. Per noi le cose sono veramente elementari.

Possiamo facilmente immaginare la curva di prima in coordinate celesti (ad esempio ascensione retta e declinazione) e tracciare la curva apparente “spaziale”, descritta da un pianeta al passare del tempo. In alto, a destra in Fig. 6, il caso complanare, in basso quello non complanare.

Fermiamoci ancora un attimo sulla parte sinistra della Fig. 6. Notate che la curva rossa attraversa TRE volte, durante un anno terrestre, l’asse del tempo, ossia annulla l’angolo ϑ. Cosa capita se l’angolo è uguale a zero? Facile a dirsi: la direzione del pianeta coincide esattamente con quella della direzione fissa. Nel caso della posizione T7 e P7 siamo all’opposizione (infatti, il Sole è esattamente alle spalle della Terra). In altre parole, in queste tre configurazioni, se siamo nel caso complanare, il pianeta passa davanti a un stella che indica proprio la direzione fissa di riferimento, giacente nel piano che contiene sia l’orbita della Terra che quella del pianeta. Lo devo proprio dire? Il pianeta eclissa tre volte, in un anno terrestre, la stella lontana.

Per uno scienziato come Aristarco (che, oltretutto, credeva nelle orbite eliocentriche) questa sarebbe stato una conclusione ovvia (sicuramente l’avrà descritta nei suoi appunti). Come conseguenza l’avrebbe applicata immediatamente alla configurazione Giove, satellite di Giove e Sole, nel caso particolare che la velocità orbitale del satellite e quella di rotazione di Giove (Aristarco era convinto, seguendo Eratostene, che la Terra ruotasse intorno al proprio asse) non fossero troppo diverse. Purtroppo, Aristarco non aveva nemmeno un binocolo e non poteva sapere che Giove possiede dei satelliti…

Siamo arrivati al “mistero” che si è sciolto come neve al Sole. Attenzione! Si è sciolto senza bisogno che ci venissero in aiuto programmi tecnologici. Basta e avanza anche meno di una matita e di un foglio. Ci vuole soltanto un minimo ragionamento che Aristarco poteva fare più di duemila anni fa. E non possiamo farlo noi oggi? Direi proprio di sì, senza alcun aiuto “esterno” preso a scatola chiusa!

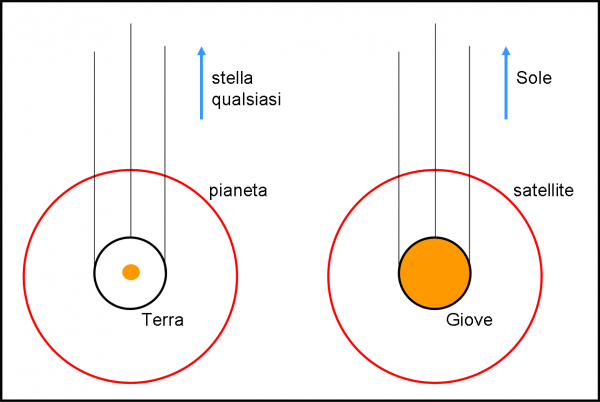
Invito i più riflessivi e volenterosi a completare l’articolo da soli, pensando a come trasformare il sistema Terra-Giove-direzione fissa nel sistema Giove-satellite-Sole e ripetere pari pari quanto fatto finora. Non potrei nemmeno dirgli: “Bravi!”, dato che farebbero né più né meno quello che hanno fatto i grandi scienziati antichi. Sì, è vero erano grandi scienziati, ma erano anche uomini che sono vissuti più di duemila anni fa… La Fig. 7 illustra il cambiamento da apportare. A sinistra quello usato finora, a destra quello da utilizzare d’ora in poi.

Noi, in ogni modo, continuiamo, sapendo ormai -per certo- che si tratta di un gioco quasi da bambini.

Al posto dell’orbita terrestre inseriamo il pianeta Giove; al posto del pianeta, il satellite di Giove e, al posto della direzione fissa, la direzione del Sole. Qualche piccola considerazione. Per semplicità abbiamo considerato l’equatore di Giove e l’orbita del satellite complanari; sullo stesso piano giace anche il Sole. Questa approssimazione è quasi del tutto verificata in Natura. Inoltre, abbiamo considerato la direzione del Sole fissa. In realtà, Giove rivolve attorno al Sole e, quindi, il Sole si sposta “apparentemente” nel cielo. Tuttavia, nell’intervallo di tempo in cui Giove compie una mezza rotazione attorno al suoi asse (e il satellite riesce a eclissare il Sole), la nostra stella può tranquillamente essere considerata ferma nel cielo. Noi non vogliamo dare numeri ultra precisi, ma solo spiegare il fenomeno. Per eseguire calcoli ultra perfetti possiamo benissimo usare uno “schiavo” molto operoso e veloce: il computer.

Consideriamo la Fig. 8.

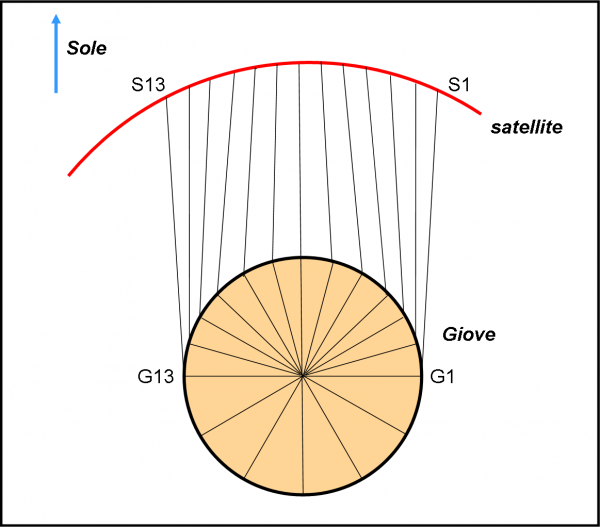
Domina Giove di cui consideriamo un punto G della sua superficie che ruota con velocità costante attorno al centro del pianeta. Purtroppo Giove è un corpo molto denso che blocca la luce. Ne segue che possiamo considerare solo la traiettoria del punto tra G1 e G13. Quando il punto della superficie passa nell’altro emisfero NON può più vedere il Sole. Bene, una semplificazione del problema: e’ come se nei casi precedenti considerassimo solo mezza orbita terrestre.

Il satellite S fa, adesso, la parte che prima faceva il pianeta. Immaginiamo che si trovi in S1 quando il punto superficiale di Giove si trova in G1. Scegliamo una velocità orbitale (costante) tale che il satellite arrivi in S13 quando Giove giunge in G13. Non ci resta che misurare gli angoli che le congiungenti G-S fanno con la direzione del Sole: lo stesso identico procedimento che abbiamo usato per la Terra e il pianeta.

Ingrandiamo la parte che ci interessa e rappresentiamola nella Fig. 9, in alto.

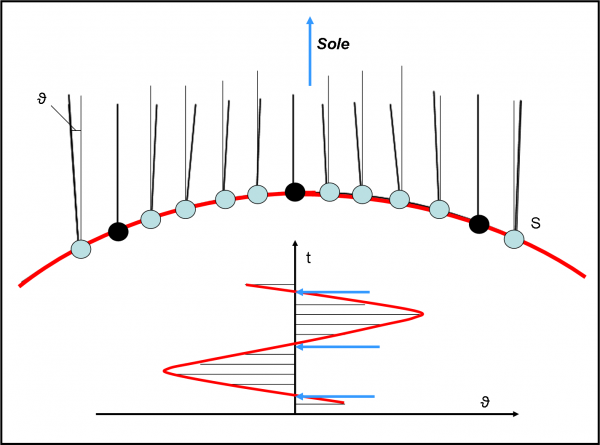
Si vedono molto bene gli angoli che vogliamo misurare e si nota molto bene che, a volte, sono positivi e a volte negativi, in modo analogo a quanto trovato precedentemente. Salta subito all’occhio che in tre posizioni del punto G, il satellite si trova nella stessa direzione del Sole e, quindi, lo eclissa. Disegniamo, comunque, nella parte bassa della figura, il nostro diagramma spazio-tempo (anzi, distanza angolare-tempo). Usiamo una scala comoda per evidenziare meglio le differenze tra gli angoli. Non ci stupiamo di certo se si ottiene la “solita” curva rossa che attraversa tre volte l’asse del tempo, ossia che annulla tre volte l’angolo tra satellite e Sole. Le frecce azzurre indicano questi momenti che sono quelli di eclissi di Sole da parte del satellite.

Ciò che la volta scorsa avevamo risolto in modo molto rozzo e rapido, l’abbiamo ritrovato in modo molto più preciso e generale. Una banalissima conseguenza del moto apparente dei pianeti sulla volta celeste. Se si conosce questo (e spero proprio di sì) si DEVE anche immediatamente capire il mistero delle tre eclissi. Sono la stessa identica cosa!

Ovviamente, dobbiamo notare che per ottenere questa configurazione è necessario che ci sia un legame tra moto orbitale del satellite e rotazione di Giove. La velocità orbitale del satellite deve essere lievemente inferiore a quella di rotazione di Giove. Noi abbiamo anche scelto le condizioni di partenza migliori perché si ottenga la soluzione voluta. In altre parole Giove e il satellite devono trovarsi nella posizione giusta al momento giusto. Ne deriva che, pur essendo elementare nella sua spiegazione, il fenomeno è estremamente raro, in realtà. Il satellite, per potersi muovere nel modo giusto, deve, inoltre, come già detto, trovarsi a una ben determinata distanza da Giove (se no Keplero si arrabbierebbe non poco). Le cose cambierebbero completamente se Giove ruotasse con un periodo diverso e se il satellite fosse più vicino o più lontano.

Ecco, a questo punto possiamo anche divertirci a fare intervenire i programmi “pappa pronta”, il cui unico servizio diventa quello di illustraci con effetti speciali quanto ormai abbiamo capito benissimo. Fare il viceversa, ossia usare la “pappa pronta” per riuscire -magari- a capire come funzionano le cose è quanto di più antiscientifico ci possa essere. Può far pensare di trovarsi di fronte a un mistero, quando, in realtà, siamo di fronte a un fenomeno conosciuto da millenni!

So benissimo che qualcuno si sarà un po’ irritato per le continue ripetizioni e -magari- anche un po’ spazientito per certe conclusioni. Tuttavia, questo articolo più che un fenomeno astronomico ha voluto trattare un modo di pensare (anzi, di “non” pensare) che sta diventando dilagante. Ci si affida alla tecnologia non solo per sfruttarla a fini estetici o pratici, ma anche -e soprattutto- per usarla come atto di fede o come metodo che aiuti a comprendere i concetti base. No, non ci siamo proprio. Se gli antichi greci avessero agito così, forse oggi saremmo ancora alla Terra piatta e al sistema geocentrico, illustrato da bellissimi e inutili programmini come Celestia e Stellarium. No, la loro ragione di esistere è solo e soltanto di comodo e di spettacolarizzazione, ma NON aiuta assolutamente a usare il proprio cervello, anzi lo disattiva sempre di più…

 

Davvero incredibili le conquiste intellettuali e scientifiche compiute nell’antica Grecia, QUI trovate una sintesi delle più importanti.

NEWS! Misurata, finalmente e direttamente grazie al VLBA, attraverso la parallasse annua, la distanza tra due punti periferici della Via Lattea: la Terra e la zona di nascite stellari denominata G007.47+00.05.