Categorie: Astronomia Elementare Satelliti e anelli
Tags: Aristarco astronomi greci distanza Luna Eratostene ipparco raggio Luna
Scritto da: Vincenzo Zappalà
Commenti:6
QUIZ geometrico: Aristarco e Ipparco, quello che -forse- non sappiamo di loro **
Continuiamo a inserire qualche semplice quiz per le “vacanze”. Questa volta la sua soluzione ci serve per sbalordirci ancora di più della grande mente degli astronomi greci. L’idea mi è venuta “spiando” di nascosto la prossima emozionante avventura di Astericcio & co., che non tarderà a uscire…
Questo è un quiz decisamente preparatorio per cercare di intuire ciò che menti eccelse come quelle di Aristarco e di Ipparco avrebbero potuto dedurre dalle osservazioni astronomiche. Da quello che ci è giunto, sono più che sicuro che il condizionale può benissimo diventare un indicativo (avrebbero = hanno).
Aristarco, basandosi sul suo sistema eliocentrico, intuì perfettamente la parallasse stellare e sbagliò la misura della distanza del Sole solo per la limitatezza della strumentazione tecnologica di allora. Tuttavia, non posso credere che un genio come lui non abbia tentato di valutare i propri errori e mettersi in condizioni di riuscire comunque a valutare la distanza tra la Terra e la Luna. Non è un caso che Ipparco, altro genio indiscusso, malgrado la sua visione eliocentrica, abbia espresso pari pari il risultato a cui Aristarco era probabilmente pervenuto. Solo un miglioramento, non un metodo innovativo. D’altra parte, Ipparco aveva già sbalordito il mondo e tutti noi con la determinazione della precessione degli equinozi.
Consideriamo questo articolo, e i seguenti, una specie di visione fantascientifica dei risultati di due grandi geni del passato. Mai, però, come questa volta sono convinto che la fantascienza possa rappresentare la realtà.
Ancora una volta, devo dire grazie a quella allegra combriccola di Astericcio & co che, mai stanchi di scoprire e di viaggiare, sono riusciti a discutere a tu per tu proprio con i grandi astronomi del passato. Non chiedetemi come diavolo hanno fatto a riuscirci (lo leggeremo tra non molto…), ma fatto sta che hanno stimolato il mio tentativo di completare ciò che la storia non ci ha tramandato, ma che sicuramente è avvenuto.
Cominciamo con un semplice QUIZ geometrico, che ci servirà nella susseguente trattazione. Un quiz che sicuramente Aristarco e Ipparco non avevano problemi a risolvere…
Tanto per avere un’idea dell’epoca e della sovrapposizione delle vite dei grandi geni greci (ho aggiunto anche Eratostene, dato che il suo risultato è fondamentale) riportiamo un semplice schema con le date di nascita e morte (non sicure, ovviamente). In particolare, è interessante notare che Aristarco poteva benissimo essere a conoscenza del raggio terrestre trovato da Eratostene.
Aristarco 310 ------------- 230
Eratostene 275 ---------------195
Ipparco 190 -------------120 a. C.
Il quiz che proponiamo è espresso in Fig. 1 (a sinistra).
Ovviamente, non rappresenta un’eclissi di Sole, ma un’eclissi di Luna, come si vede bene attraverso le due immagini reali riportate a destra. Il problema è: “Come determinare GRAFICAMENTE il rapporto dei raggi dell’ombra terrestre e della Luna?”. Questo rapporto è essenziale per il calcolo della distanza della Luna, e non solo. Non rispondete: “Cercando di approssimare con una circonferenza l’arco dell’ombra terrestre…”. Vogliamo qualcosa di più accurato.
Permettetemi una riflessione piuttosto ovvia (ma che tale non è più sembrata nei secoli successivi). L'ombra della Terra è CIRCOLARE. Così come sono circolari le immagini del Sole e della Luna. Possiamo veramente meravigliarci se Eratostene ha considerato come un dato di fatto che la Terra avesse una forma sferica? Mah... la conclusione è talmente ovvia che stupisce molto di più accettare gli assurdi modelli posteriori...
Alla prossima…
Soluzione QUI
6 commenti
Credo anch'io che questi Greci sapessero molte più cose di quello che ci è giunto fino a noi.Probabilmente questo non è dovuto al genio dei protagonisti di quel periodo,ma alla forma mentis che imperava tra gli eruditi del tempo,dove gli Dei erano democratici e tolleranti e non pervasivi,assiomatici e asfissianti come lo sono diventati dopo.La possibilità che un gruppo di sconsiderati pieghino ai loro interessi una certa intellighenzia mercenaria,sfruttando la creduloneria e la voglia di cose nuove della gente è sempre dietro l'angolo,poi ci pensa il tempo ad offuscare molte menti tanto dicono:ipse Dixit .
Visto che oggi è domenica e la gente è in vacanza vi propongo un vecchio intermezzo:
Una vedova risponde alle amiche che la consigliano vivamente di sposarsi:
-Non vedo il perché,ho un cane,un pappagallo e un gatto.
-Va bene,tutti questi animali ti tengono compagnia,ma non sostituiscono certamente un uomo...
-Come no?Il cane brontola tutto il giorno,il pappagallo bestemmia dalla mattina alla sera,e il gatto sta via tutta la notte.
Notte gente!
Provo a dare una risposta a questo QUIZ anche se, come dirò di seguito, vedo ancora dei problemi con la soluzione che propongo.
Il primo passo è quello di misurare l'angolo)
sotto il quale si vede la Luna.
Se
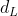è la distanza della Luna ed 
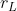il raggio della Luna, vale questa relazione =\frac{r_L}{d_L})
che approssimativamente è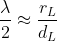 
Nella figura 1 del QUIZ si vede il cono d'ombra della terra, normalmente invisibile, proiettato sulla superficie della Luna. Come un'ombra cinese.
Il raggio del cono d'ombra, che si riduce allontanandosi dalla Terra, nella figura 1 è quello alla distanza della Luna (circa).
Una possibilità è quella di misurare l'angolo tra il centro della gobba e l'asse del cono d'ombra, il triangolo rosso in questa figura.
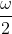questo angolo e mi accontento di approssimare la distanza dell'ombra con la distanza della Luna varrebbe la relazione =\frac{r_o}{d_L})
dove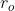 
è il raggio del cono d'ombra.
Se chiamo
Quindi il rapporto tra raggio dell'ombra e raggio della Luna sarebbe
}{sin\left&space;(&space;\frac{\lambda}{2}&space;\right&space;)}\approx&space;\frac{\omega}{\lambda}})
Credo ci siano (almeno) due problemi con questa soluzione.
La distanza alla quale misuro l'ombra è minore di quella del centro della Luna e non è determinabile perchè varia con la posizione dell'ombra sulla Luna. Il QUIZ mi sembra richieda di non fare questa aprossimazione quando chiede di "non approssimare con una circonferenza l’arco dell’ombra terrestre…”
Inoltre credo ci sia un problema pratico perchè l'asse del cono d'ombra non è qualcosa di visibile.
L'alternativa potrebbe essere quella di misurare l'angolo tra l'ultimo punto illuminato della Luna prima di entrare completamente nel cono d'ombra ed il primo punto della Luna che esce dall'ombra (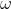
, essendo il doppio di quello misurato prima). Triangolo rosso nella figura.
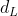, ma almeno si può ricavare dal triangolo rattangolo in verde in figura: 
.
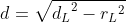In questo caso la distanza non è proprio la distanza
La relazione tra raggio dell'ombra e raggio della Luna diventa più complessa
I due punti che devo misurare sono entrambi visibili anche se non contemporaneamente.
Qui il problema è che devo assumere l'orbita della Luna complanare con quella della Terra, che è una ulteriore aprossimazione.
caro Fabrizio,
quando scrivo: "non approssimare con una circonferenza l’arco dell’ombra terrestre" voglio solo dire di non cercare di far passare una circonferenza nel pezzo visibile che l'approssimi al meglio. Voglio qualcosa di leggermente più accurato... Lavorando solo con la figura rappresentata...
Ci provo ancora considero solo la fig.1 dell'articolo che considero come l'intersezione tra il cerchio della Luna e il cerchio dell'ombra terrestre.
Il segmento tra le due punte della falce è un corda sia per il cerchio della Luna sia per il cerchio dell'ombra terrestre.
La relazione generale tra semi-corda e raggio di un cerchio può essere ottenuta applicando il teorema di Pitagora al triangolo in rosso di questa figura.
Posso applicare questo risultato sia al cerchio della Luna sia al cerchio dell'ombra della terra, ottenendo:
Poichè le semicorde sono le stesse, posso uguagliare i due termini a destra
Le altezze dei segmenti circolari possono essere ottenute misurando gli angoli il figura.