Questo articolo è stato inserito nella sezione d'archivio "Antichi Greci, che passione!"

 

Risolviamo subito il piccolo problema geometrico (QUI) che ci regala un fondamentale rapporto, che lega strettamente dimensioni e distanza. Poi ci dedichiamo a una determinazione che ha dello sbalorditivo.

La soluzione si trova ricordando una caratteristica delle circonferenze: data una qualsiasi corda, la sua normale, tracciata nel punto di mezzo, deve passare per il centro della circonferenza (se non vi convince, provate a dimostrarlo…)

Consideriamo allora la Fig. 2, dove è rappresentato lo “spicchio” di Luna creato dall’ombra terrestre. La superficie lunare è indicata dall’arco AMB, mentre l’ombra terrestre è indicata da ANB. Ciò che vogliamo trovare è il rapporto tra i raggi delle due circonferenze. Tracciamo la verticale MN che taglia esattamente a metà i due archi. A questo punto, disegniamo le corde uguali AM e MB. Esse appartengono alla circonferenza-Luna. Tracciamone le perpendicolari nel loro punto di mezzo: il punto d’intersezione è, ovviamente, il centro L della circonferenza-Luna (tutte e due devono passare per il centro…).

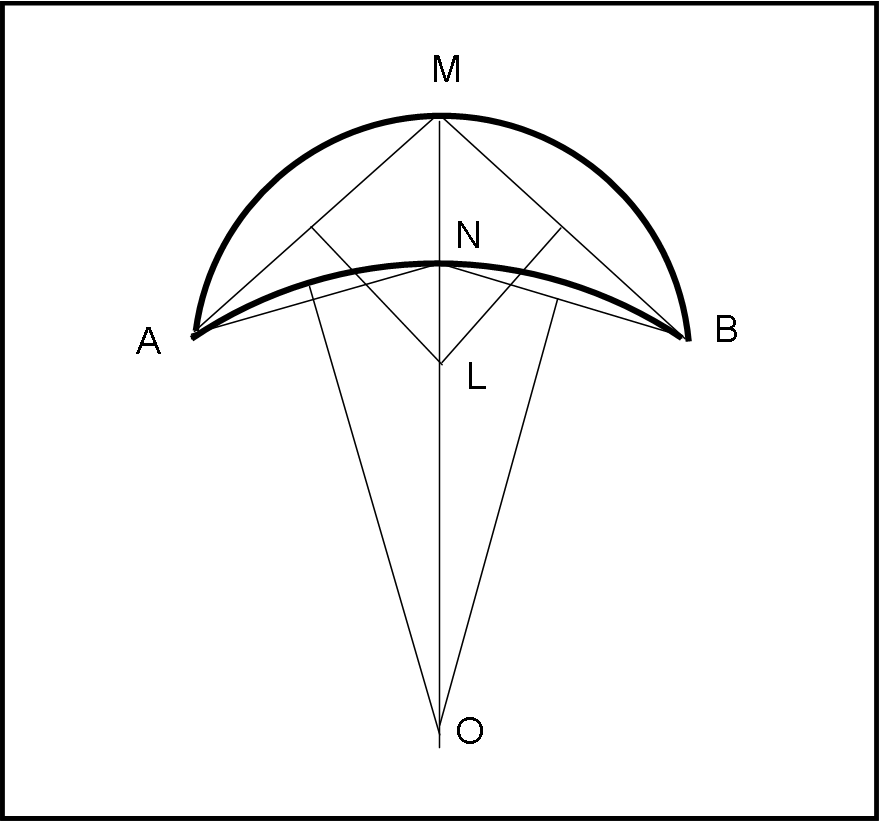
Eseguiamo una costruzione analoga sulla circonferenza-ombra e otteniamo le due normali alle corde (uguali) AN e NB. La loro intersezione è in centro della circonferenza-ombra.

Il rapporto tra i due raggi così trovati regala il valore richiesto. L’errore che si commette eseguendo ripetute misurazioni (magari anche in occasioni diverse) è relativamente piccolo.

Risolto il QUIZ e con il primo dato nelle nostre mani, dirigiamoci verso il metodo di determinazione della distanza lunare, sicuramente alla portata della mente e della tecnologia di Aristarco (e ancor più di Ipparco). Prima, però, riassumiamo la situazione di quei secoli così meravigliosi per il cervello umano.

Dati di fatto:

1) Aristarco sapeva che il disco apparente della Luna era uguale al disco apparente del Sole

2) Aristarco sapeva che l’ombra in cui si immerge la Luna durante un’eclissi è quella della Terra, causata dalla luce solare

3) Aristarco conosceva il raggio della Terra in chilometri (o quello che era) attraverso la determinazione di Eratostene.

4) Aristarco aveva sicuramente intuito che il Sole era decisamente più distante rispetto al valore trovato da lui. In fondo, ammetteva senza problemi che le stelle fossero a distanze enormi. Inoltre, Eratostene aveva già assunto per il Sole una distanza praticamente infinita (Aristarco non poteva ignorarlo).

Problemi:

1) La misurazione degli angoli. Tuttavia, una cosa è misurare con precisione un angolo che è quasi 90°  la cui minima imprecisione porta a errori enormi sulle distanze e un’altra è misurare direttamente il disco della Luna. Esistevano, comunque, vari metodi…

2) La conoscenza della trigonometria. Alcuni dicono che l’abbia “inventata” Ipparco, ma, di fatto, veniva usata in modo più o meno empirico anche prima. La differenza temporale tra le vite di Aristarco e Ipparco è troppo breve per pensare a una vera rivoluzione. Probabilmente Ipparco ha migliorato gli strumenti di misura degli angoli, ma si è ispirato sicuramente al metodo proposto (ed eseguito?) da Aristarco.

“Chi ha fatto cosa” forse non si saprà mai. Ma, senza alcun dubbio il trio Eratostene-Aristarco-Ipparco ha sicuramente permesso di stabilire la distanza della Luna. Un passo decisivo e fondamentale per rendere tridimensionale lo spazio. Se poi, a questa determinazione si aggiunge quella del raggio terrestre e l’estrema lontananza delle stelle, si comincia veramente ad avere una “mappa” entusiasmante dell’Universo. Una conquista che andrebbe pubblicizzata molto di più di quanto non si faccia. Forse perfino più importante del moto eliocentrico… Ipparco, infatti, ha trovato la precessione senza curarsi più di tanto di chi fosse a girare intorno all’altro. Ma lo stesso Aristarco sembra che ammettesse l’importanza relativa di questa scelta per la misura delle distanze.

Fatte queste premesse, svolgiamo il nostro compito, cercando di immedesimarci in Aristarco (e Ipparco) e di determinare “a modo loro” la distanza della Luna… ne vedremo delle belle!

La figura di riferimento è la Fig. 3, dove sono rappresentati il Sole, la Terra e la Luna, durante un’eclissi di Luna. Le proporzioni non sono, ovviamente, rispettate, ma non creano problemi, se non nel caso di due triangoli simili che vedremo tra poco. La tabellina esplicativa della figura indica le varie grandezze in gioco.

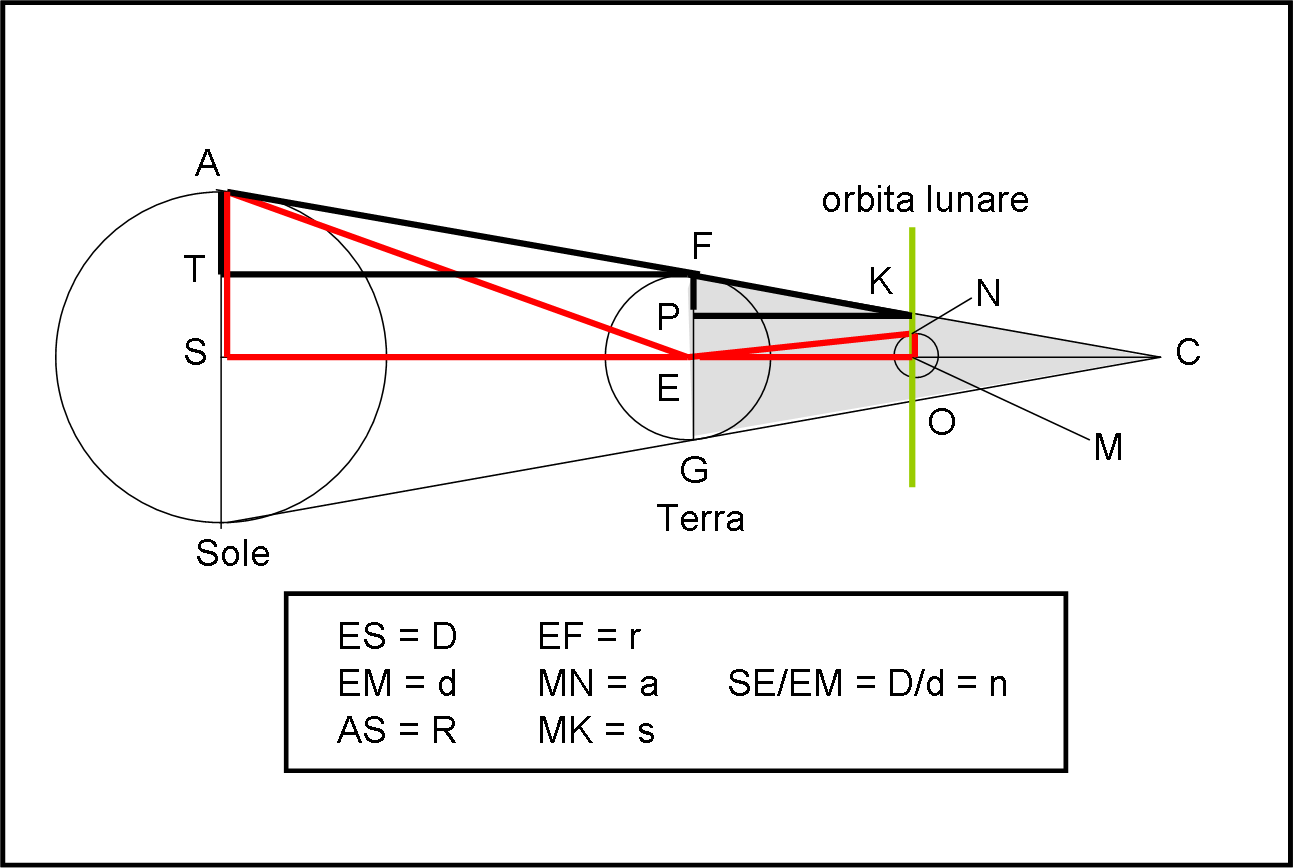
L’ultima grandezza (n) è la più critica, dato che indica il rapporto tra la distanza del Sole e quella della Luna. Proprio riguardo a lei, dobbiamo evidenziare un’apparente errore nella figura. Sarebbe, infatti, impossibile disegnare in scala le distanze del Sole e della Luna e quindi la seconda è stata notevolmente aumentata. Tuttavia, ci viene in soccorso l’eclissi di Sole. Essa dice (e lo diceva già ai tempi di Aristarco & co.) che il disco apparente solare è uguale al disco apparente lunare. Ne segue che dalla Terra entrambi i corpi celesti si vedono sotto lo stesso angolo. Ne segue che i due triangoli rossi sono SIMILI. Infatti, i due triangoli sono rettangoli e i due angoli in E sono uguali. Ne segue che la relazione che esiste tra d e D è la stessa che esiste tra a e R.

Possiamo scrivere:

n = R/a

Sono anche simili i due triangoli rettangoli ATF e FPK. Da cui:

AT/FP = TF/PK =  SE/EM

AT/FP = (AS – FE)/(FE – KM)

SE/EM = (AS – FE)/(FE – KM)

D/d = (R – r)/(r – s)

n = (R – r)/(r – s)

Ricordando che n = R/a

n = (na – r)/(r – s)

nr – ns = na – r

nr + r = na + ns

nr + r = na (1 + s/a)

nr (1 + 1/n) = na (1 + s/a)

a (1 + s/a) = r(1 + 1/n)          …. (1)

La (1) è una relazione che sarà utilissima tra poco…

Vediamo cosa conosciamo e cosa riusciamo a misurare.

Innanzitutto, il quiz della volta scorsa ci ha fornito graficamente il rapporto s/a

Il metodo di Eratostene ci ha fornito il valore della circonferenza terrestre e quindi il suo raggio r

 Ed eccoci alla parte più “difficile”: la misura del diametro angolare della Luna (o del Sole) φ

 Vi sono almeno due metodi che personaggi come Aristarco e Ipparco avrebbero potuto usare (pur non conoscendo o conoscendo in parte la trigonometria): uno diretto e uno indiretto.

Accenniamo a entrambi in modo molto rozzo, con l’aiuto della Fig.  4 (i nostri grandi amici greci avrebbero sicuramente fatto di meglio). In alto, il metodo diretto applicato alla Luna. Basta utilizzare un dischetto o una sferetta di diametro qualsiasi e cercare l’esatta sovrapposizione con il disco lunare. L’arco sotteso dal dischetto è esattamente lo stesso sotteso dalla Luna. Conoscendo la distanza del dischetto L e il suo diametro, si ricava l’angolo φ.

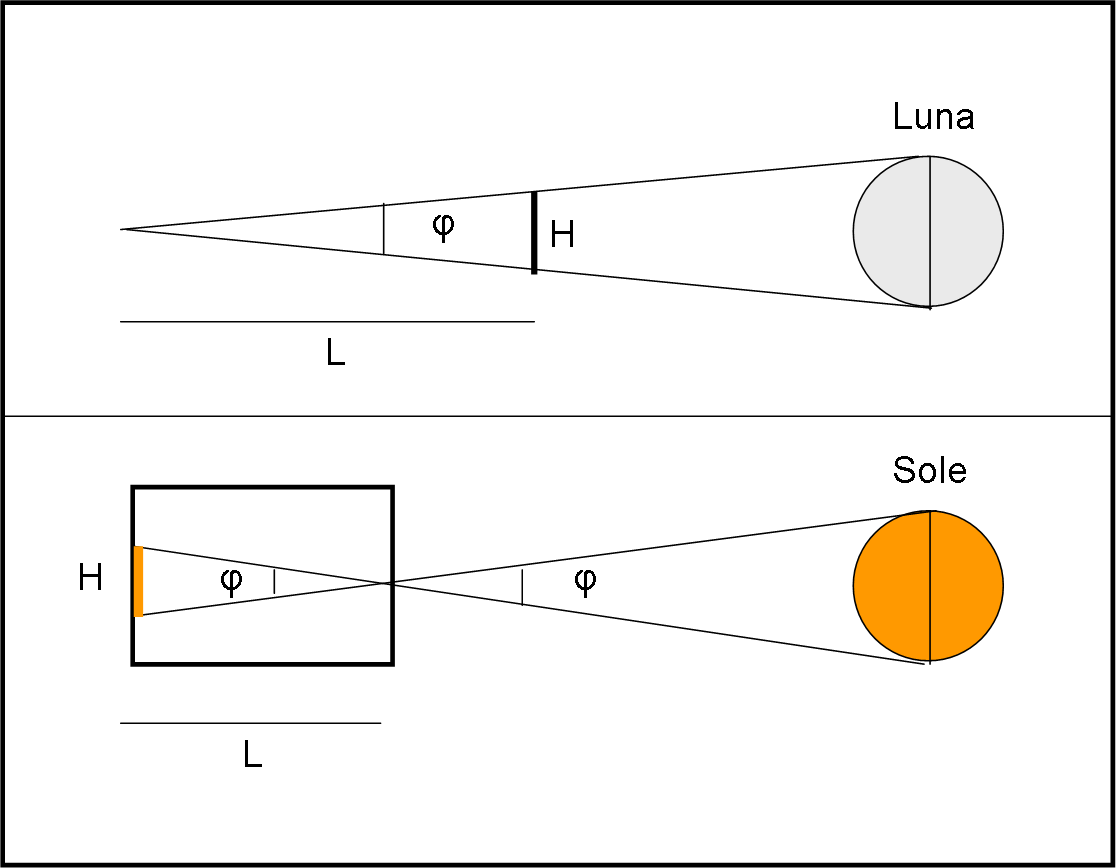
Il secondo è indiretto e si riferisce al disco solare. Basta costruire una camera oscura con un foro stenopeico su un lato (ossia un foro molto piccolo). La luce del Sole entra attraverso il piccolo foro e illumina la parete di fronte riproducendo la sua immagine invertita. Un disegnatore può benissimo mettere in evidenza la circonferenza contenente l’immagine del Sole e, in base alla distanza del foro L e al raggio della circonferenza, si trova l’angolo φ.

Ricordiamo che il concetto di “camera oscura” era già ben noto sia nell’antica Cina che in Grecia (ne parla anche Aristotetele). Molti conoscono questo effetto osservando le tante immagini a forma di falce di Luna (o meglio, falce di Sole), durante le eclissi anche parziali di Sole. La luce solare filtra nei piccoli fori tra le foglie e i rami degli alberi, formando, al suolo, moltissime immagini a falce.

Personalmente, sono certo che un grande numero di misurazioni e un miglioramento di entrambe le tecniche abbiano potuto fornire valori più che accettabili di φ.

Il raggio della Luna a e il suo diametro angolare φ sono legati da una semplice relazione:

a = d tan(φ/2)        …. (2)

Abbiamo due incognite (a e d). Un bel problema…

Non ci resta che riprendere in mano l’equazione (1) che poteva essere facilmente ricavata dai nostri geni. Si conosce tutto, tranne n.

In un suo precedente studio, Aristarco aveva cercato di misurare n (ossia quante volte il Sole è più distante della Luna) e aveva trovato un valore troppo piccolo, circa 20. Lui stesso non lo accettò  come realistico. Non sappiamo se abbia mai affrontato ciò che stiamo per descrivere. Tuttavia, il fatto stesso che Ipparco lo applicò senza troppa enfasi, potrebbe essere un segno del tentativo di Aristarco. Riportiamo, comunque, i valori utilizzati da Ipparco:

s/a = 8/3

φ = 31’

r = 6500 km (da Eratostene)

Ed ecco il punto decisivo che nasce combinando la (1) e la (2) e sostituendo i valori ottenuti da Ipparco

 a (1 + s/a) = r(1 + 1/n)

 d = a/tan(φ/2)

 a = d tan (φ/2) = d tan (15.5’)

 a = d/220

(d/220)(1 + s/a) = r(1 + 1/n)

d (1 + 8/3)/220  = 6500 (1 + 1/n)

0.0167 d = 6500 (1 + 1/n)

d = 6500 (1 + 1/n)/0.0167    …. (3)

Se il Sole è veramente molto più lontano della Luna (Eratostene, in fondo, l’aveva assunto tale), possiamo anche dire che n è enormemente più grande di 1, talmente grande che possiamo anche considerare 1/n tendente a ZERO. La (3) ci permette, comunque, di variare, a piacere, il rapporto tra distanza solare e lunare. Nel caso limite di 1/n = 0, si ottiene:

d = 390 000 km

a (1 + s/a) = r

a = r/(1 + s/a)

a = 6500/(1 + 8/3) = 1773 km

2a = 3545 km

 Se li confrontiamo con i valori medi odierni

 d_N = 384 404 km

 2a_N = 3476 km

non possiamo che toglierci tanto di cappello: grande Ipparco, ma altrettanto grande (se non di più), Aristarco, che potrebbe benissimo aver ottenuto un risultato del tutto simile (purtroppo i suoi risultati non sono stati mai divulgati adeguatamente).

Lo spazio a tre dimensioni aveva iniziato a formarsi… Sarebbe bastata la parallasse solare e il Sistema Solare sarebbe diventato una casa ben conosciuta.