Categorie: Meccanica Celeste Sistema Solare
Tags: forza gravitazionale leggi di Keplero orbite stabili problema 3 corpi satelliti artificiali
Scritto da: Vincenzo Zappalà
Commenti:28
La sfera di Hill **
La sfera di Hill risponde alla seguente domanda: “Dato un piccolo corpo (un pianeta, ad esempio) che rivolve attorno a un corpo decisamente più grande (una stella), può il corpo minore avere un satellite stabile?”
In altre parole, apparentemente più tecniche: essa è la regione di spazio contenente un corpo di massa M2, nella quale la forza gravitazionale che M2 esercita su un satellite è maggiore della forza gravitazionale che esercita su di lui il corpo di massa M1, attorno a cui orbita il corpo di massa M2. In poche parole, è come se per il satellite esistesse soltanto il pianeta di massa M2 (anche se è obbligato a girare insieme a lui attorno alla stella M1).
Qualsiasi definizione meriterebbe una discussione… In realtà, il satellite è, comunque, costretto a rivolvere attorno al corpo principale (pensate alla Luna). Non può, quindi, essere considerato “staccato” da questa massa che gioca ancora il ruolo più importante. In qualche modo, usiamo un sistema di riferimento locale, pur partendo da un sistema ben più ampio. Qualcuno pensa di definire il moto orbitale di un satellite come una rivoluzione attorno al corpo M1 sotto la perturbazione del corpo minore M2. Una specie di ribaltamento della situazione. Si potrebbe discutere a lungo, ma ciò che veramente importa è l’applicazione pratica e quindi dedichiamoci alla determinazione del raggio della sfera di Hill, che sarà, ovviamente, approssimata.
Vi sono vari metodi per calcolare il raggio della sfera di Hill. Una derivazione formalmente esatta va oltre lo scopo del nostro “circolo” e rimane, comunque, legata a particolari condizioni. La difficoltà è abbastanza intuitiva: essa vuole fornire un risultato “pratico” e quindi deve tener conto di tutti quei fenomeni che alterano una trattazione puramente teorica. Siamo di fronte a un’orbita che risente delle perturbazioni esterne. Come si nomina la parola “perturbazioni” qualsiasi teoria analitica entra in crisi. Basta ricordare che il semplicissimo problema dei tre corpi è ancora irrisolvibile analiticamente nel caso più generale (si risolve solo per casi particolari come vedremo in seguito). Ne segue che è del tutto inutile sprecare troppi calcoli per definire una regione di spazio che risente di una quantità enorme di effetti secondari in grado di stravolgere il risultato cercato. Possiamo anche permetterci di considerare le orbite circolari.
Partiamo, quindi, dalla sua definizione e poniamo un limite che è più che logico nella sua semplicità: se un oggetto deve subire una forza gravitazionale, da parte di un pianeta, maggiore di quella della stella attorno a cui il pianeta orbita, il limite superiore deve portare a un valore identico delle forze esercitate su di lui da parte dei due corpi.
La definizione è, infatti (ricordiamola ancora): la regione di spazio, considerata sferica, contenente il pianeta, nella quale la forza gravitazionale che esercita il pianeta sul satellite è maggiore della forza gravitazionale del Sole sul satellite.
Per ottenere una stima del raggio di Hill basta, allora, porre la velocità orbitale del satellite attorno al pianeta uguale alla velocità orbitale del satellite attorno al Sole. In tal modo, l'influenza gravitazionale del Sole è "circa" uguale a quella del pianeta. Determinando la distanza pianeta-satellite, si determina automaticamente il raggio della sfera di Hill.
Per descrivere la velocità orbitale basta utilizzare la terza legge di Keplero in cui si considera trascurabile la massa del terzo corpo e l’orbita è assunta circolare, ossia a = r = costante. Essa dice:
4π2 /P2 = GM/r3
Il primo membro non è altro che la velocità orbitale ω (costante) al quadrato, quindi:
ω2 = GM/r3
Sia M1 la massa del corpo principale (il Sole, ad esempio) e M2 la massa del pianeta (la Terra, ad esempio) attorno a cui vogliamo fare orbitare il satellite.
Scriviamo la legge di Keplero per le due masse:
ω12= GM1/r13
ω22= GM2/r23
ovviamente, r2 non è altro che il raggio della sfera di Hill del pianeta di massa M2.
Uguagliando si ha:
GM1/r13 = GM2/r23
r23 = r13 M2/M1
r2 = r1(M2/M1)1/3
Questa soluzione deriva da un’approssimazione, più che accettabile, essenzialmente corretta, eseguita probabilmente da un caro amico e collega (non ne sono completamente sicuro, ma la “mano” è la sua), Andrea Milani, dell’Università di Pisa, dal carattere non facile, ma dalla mente matematica eccezionale. Insomma, un perfetto meccanico celeste, sicuramente uno dei migliori al mondo.
Rispetto ad altre determinazioni, manca un coefficiente 1/(3)1/3
rH = r1(M2/3M1)1/3
O, nel caso di un’orbita ellittica:
rH = a(1-e)(M2/3M1)1/3
La differenza, considerando quanto sia aleatorio il valore massimo del raggio della sfera di Hill, è del tutto trascurabile. Potremmo anche ricavare con una serie di formule un po’ più lunga il valore più noto e usato. Tuttavia, non ne vale la pena, se si pensa che si sta, normalmente, ben al di sotto del valore limite.
Simulazioni numeriche molto accurate hanno, infatti, dimostrato che le orbite prossime al valore limite non sono affatto stabili su periodi di tempo abbastanza lunghi. Per essere sicuri si accettano valori del raggio compresi tra 1/3 e 2/3 del raggio di Hill.
Con le formulette riportate, potrete divertirvi un sacco… cercando la sfera di Hill attorno a pianeti, satelliti e addirittura satelliti di satelliti. L’importante è che si abbia un corpo decisamente più massiccio e uno nettamente inferiore (in orbita attorno al primo). Noterete che non è assolutamente detto che ogni corpo minore possa tenere in orbita qualcosa. La sua sfera di Hill potrebbe essere, infatti, più piccola delle dimensioni del corpo secondario.
Basta fare un semplicissimo esempio. Consideriamo la Terra come oggetto di grande massa e la stazione spaziale come il corpo minore. La domanda è: “Qual è la sfera di Hill della stazione spaziale?”, ovvero: “E’ possibile per un’astronauta inserirsi in orbita attorno a lei?”. La risposta non è difficile… La stessa cosa si può fare per uno Shuttle su orbita bassa e cento altri manufatti umani o naturali (satelliti di Marte, ad esempio).
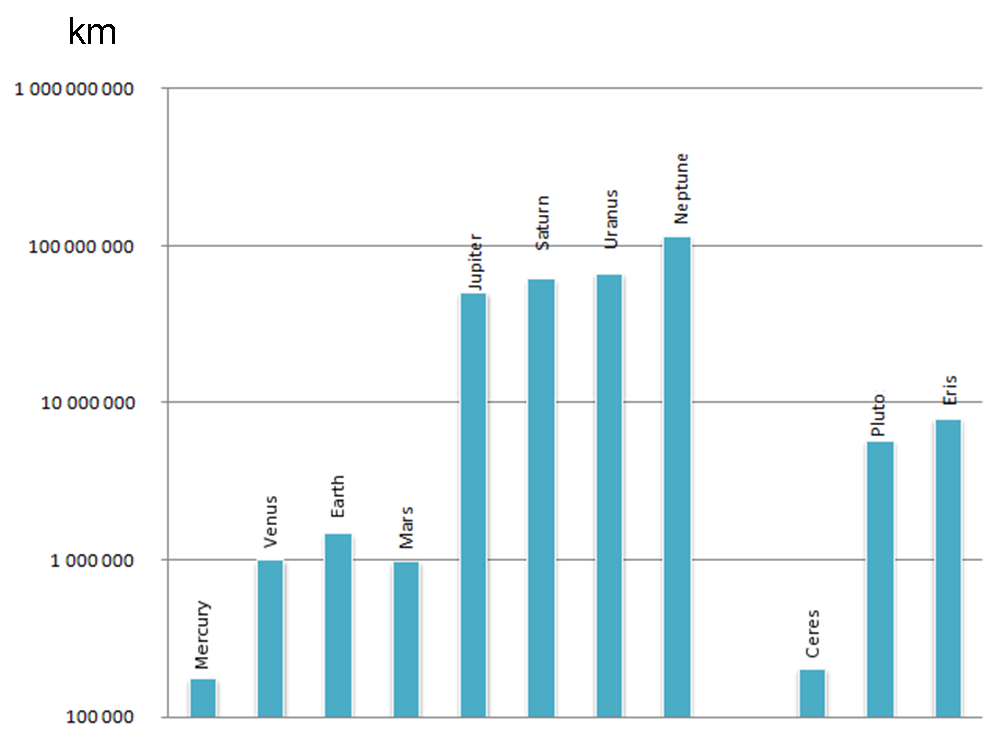
Ci siamo già accorti che il raggio di Hill dipende dal rapporto di massa tra i corpi coinvolti e dalla distanza a cui rivolve il secondario rispetto al primario. Per concludere, allora, riportiamo una figura che rappresenta i raggi delle sfere di Hill dei pianeti (e di qualche pianeta nano) del Sistema Solare. Chi vince? Come vedete non Giove, ma Nettuno. A volte la distanza vince sulla massa…
Un rapido confronto con i punti lagrangiani L1 e L2, per i più preparati (ma ci torneremo sopra in un prossimo articolo). La sfera di Hill deve ovviamente essere compresa tra questi due punti, ma non può coincidere con loro, dato che un’orbita uscirebbe dalla zona stabile e comporterebbe una lenta deriva. La sfera di Hill deve essere più piccola del lobo di Roche, anche se qualcuno la fa coincidere. Il succo del discorso non è tanto la differenza matematica della derivazione, ma il concetto stesso della definizione. Non ha quindi senso fare confronti… Restano concetti diversi che servono per determinazioni diverse.






28 commenti
Scusa Enzo, non mi è chiaro il motivo per cui parli di basi concettuali DIVERSE nel calcolo del raggio di Hill rispetto ai punti lagrangiani.
A me sembra che la differenza stia a valle piuttosto che a monte.
L'uguaglianza delle velocità angolari di μ (satellite) intorno ad M2 (pianeta) e di μ intorno ad M1 (stella) è la stessa condizione che consente di trovare i punti di Lagrange.
Il fatto di applicare un coefficiente riduttivo (1/3 o 1/2 o quello che volete) per essere certi di sfuggire alle perturbazioni rientra in considerazioni empiriche che garantiscano ragionevolmente la conservazione dell'orbita del satellite intorno al pianeta.
Dunque... i punti lagrangiani si trovano come condizioni di equilibrio nel problema dei tre corpi. Sono perciò dei punti che devono soddisfare particolari condizioni. Poco interessa se in quella posizione un corpo orbita oppure no. L'importante è che per qualsiasi piccolo spostamento esso cade verso la massa M1 o la massa M2 oppure segue un'orbita più o meno complessa. Per determinarli è necessario lavorare con il campo gravitazionale e quello centrifugo. Dai punti lagrangiani derivano le superfici equipotenziali che li determinano come punti particolari di intersezione di linee. Cadiamo quindi nei lobi di Roche che niente hanno a che vedere con un'eventuale orbita, dato che al loro interno un'orbita potrebbe anche essere instabile. Tra L1 e L2, però, esiste una regione in cui un'orbita potrebbe essere stabile su tempi molto lunghi. Quella regione è la sfera d'influenza o sfera di Hill. Se vai a vedere attentamente, i punti lagrangiani si determinano attraverso delle equazioni di quinto grado e non certo solo attraverso le semplici considerazioni fatte per la sfera di Hill. Ripeto ancora, a prima vista sembra lo stesso problema, ma la determinazione è alquanto diversa, proprio per ciò che devono rappresentare nello spazio delle due due masse rotanti attorno al proprio baricentro.
Può sembrare "lana caprina", ma in realtà affrontano problematiche del tutto diverse. Spero di farmi capire meglio quando imposterò il problema dei tre corpi risolto da Lagrange...
Alt, fermi tutti! Vediamo se ho capito.
Analizziamo le condizioni poste nel calcolo del raggio della sfera di Hill.
1^ condizione (1^ equazione di equilibrio): il satellite è in orbita (circolare) intorno al pianeta, con una determinata velocità angolare ω, quella che equilibra l’attrazione gravitazionale del pianeta.
2^ condizione (2^ equazione di equilibrio): il satellite ruoti anche, insieme al pianeta, intorno alla stella (orbita circolare) con la stessa velocità angolare ω.
Assunzione: dal modo in cui sono impostate le equazioni di equilibrio si capisce che il satellite ha massa trascurabile rispetto al pianeta; il centro di massa del sistema è infatti considerato coincidente con il centro del pianeta. Stesso discorso per la coppia satellite-stella.
Deduzione: la velocità periferica media del satellite intorno alla stella equivale alla velocità periferica del pianeta, sempre intorno alla stella. Analogamente, la distanza media del satellite dalla stella equivale alla distanza del pianeta dalla stella. Sotto queste ipotesi si può concludere che il pianeta ruota intorno alla stella con la stessa velocità angolare ω.
Se questo è vero allora la massa del pianeta deve essere trascurabile rispetto a quella della stella. In pratica il pianeta si comporta, rispetto alla stella, come si comporta il satellite.
Abbiamo quindi posto, implicitamente, una condizione supplementare che non si trova nel caso del calcolo dei lagrangiani. Quando la massa del pianeta è trascurabile rispetto alla massa della stella, il raggio di Hill coincide con la distanza di L1 dal pianeta.
E nella situazione generale? Facciamo un calcoletto.
--------------------------------------------
Calcolo del raggio della sfera di Hill nel sistema Terra-Luna:
Rh = R*(Ml/Mt)^1/3
Si ottiene che:
Rh ≈ 89.500 km
Per il punto L1 (ho trovato il valore sul web):
L1 ≈ 323.000 km
La discrepanza mi pare possa essere addebitata al fatto che la massa della Luna, pur essendo solo 1/100 di quella terrestre, non è trascurabile rispetto a quella.
Si vede, tra l'altro, come il raggio della sfera di Hill cada ben all'interno del punto L1.
Sic stantibus rebus, altro che lana caprina, caro Enzo!
O no?
Pardon, ho mancato di fare la conversione:
L1 (visto dalla Luna): 384-323 = 61.000 km.
In effetti il raggio di Hill è maggiore di L1.
caro Alvy,
hai corretto prima che ti riprendessi... bravo!(acci!)
se correggi del fattore 1/radice cubica di 3 trovi che i valori sono praticamente coincidenti. Tieni conto, comunque, che la sfera di Hill serve soprattutto per i satelliti artificiali della Terra e il sistema è quello Terra-Sole...
Puoi avere un'idea immediata guardando il lobo di Roche che è come una goccia, mentre la sfera di Hill è una sfera per definizione. Chiaramente se una massa diventa trascurabile le cose si assomigliano sempre più...
Fiiuuuuuu!!!!
Stavolta ho rischiato di brutto....
Comunque, meglio circolari che ottusi ...
Va bene, va bene... se non lo faccio prima io, tra poco Alvy mi chiederà sicuramente come arrivarci... insomma, mi metto a scrivere una seconda parte della sfera di Hill, quella in cui si può derivare la formula più usata...
Riuscirò a non strozzarlo? Mah... si salva solo perché gli alieni sono una razza... protetta!
GRANDE ENZONE ....
Mi raccomando Enzo, mi aspetto una bella ed esaustiva trattazione
A proposito, che fine hanno fatto i nostri amici papalli? Secondo me si stanno annoiando. Perchè non organizzi qualche altra festa (con relativo quiz)?
faccio quello che posso... ma che non serva per innescare nuovi voli alviarici... Accontentati ogni tanto! Cosa avete studiato fino ad oggi sul vostro assurdo pianeta' Non avevate qualche fiction o reality show da guardare con gli occhi a ... papalla!
Accontentati ogni tanto! Cosa avete studiato fino ad oggi sul vostro assurdo pianeta' Non avevate qualche fiction o reality show da guardare con gli occhi a ... papalla! 
Ma, Enzo, credevo lo sapessi. Noi non viviamo su di un pianeta: siamo puro pensiero, liberi di vagare per il cosmo. L'Universo è la nostra casa. Possiamo essere contemporaneamente qui e là, nel presente e nel passato.
Siete stati visitati, nel tempo, da alcuni nostri emissari aventi lo scopo di civilizzarvi un pochino. Avete attribuito loro dei nomi a voi familiari come Albert, Richard, Charles ...
Mi sembra non ne abbiate tratto gran profitto se banali idee come la relatività e la meccanica quantistica sono note solo ad una piccolissima percentuale di umani.
Per noi sono giochini equiparabili alle vostre parole crociate facilitate.
Beh, ci sentiamo domani, ora vado a fare un mental-giro del cosmo, sai com'è, sono stato invitato da alcuni amici per il fine settimana... e loro abitano a circa 50.000.000.000 di a/l da voi.
Si, non ti spaventare, sono oltre il bordo dell'Universo osservabile (per voi...)
puahhh!!! Fantascienza di serie B.... trovane un'altra
Dai Prof., devi ammettere che, anche se sembrano usciti da una serie di telefilm di fantascienza di serie B, questi Circolari Circoncisi sono più simpatici dei Papalliani!!!
ma sì Daniela... hai ragione! Accettiamoli come sono... poverini, anche loro hanno diritto di vivere nell'Universo (e di rompere...)
Caro Enzo pur non conoscendo la Terza Legge di Keplero , quando ho visto la formula di partenza mi sono accorto che aveva qualcosa di famigliare.
, quando ho visto la formula di partenza mi sono accorto che aveva qualcosa di famigliare.
Una formula simile l'avevo ricavata per rispondere al problemino che ponevi nell'articolo sull'esistenza o meno della Forza centrifuga -Parte 4
http://www.infinitoteatrodelcosmo.it/2014/05/18/esiste-la-forza-centrifuga-quarta-parte/
Infatti, dato che in un moto circolare uniforme la velocità è costante, quest'ultima può essere facilmente calcolata dividendo la circonferenza (2π r) per il tempo impiegato per percorrerla, ossia il periodo P necessario per compiere un giro completo:
v = 2π r/P
Ma un satellite per rimanere in orbita e muoversi con moto circolare uniforme, deve possedere una velocità tangenziale tale da compensare l'accelerazione centripeta:
aC = v²/r
Sostituendo si ottiene:
aC = (2π r/P)²/r = 4π² r² /P² r
aC = 4π²r/P²
Dato che l'accelerazione centripeta in questo caso è rappresentata da quella di gravità: a = GM/r²
Eguagliando le due relazioni trovate per determinare l'accelerazione centripeta, si ottiene:
GM/r² = 4π² r/P²
4π²/P² = GM/r³
Nello svolgere queste brevi operazioni (che spero siano corrette) mi sono accorto e volevo segnalarti un piccolo refuso, ossia nella formula iniziale il π dovrebbe essere elevato al quadrato.
Infine, giusto per divertirsi ad applicare il contenuto di questo articolo, ho provato a stimare la sfera di Hill della stazione spaziale internazionale.
Partendo dai seguenti dati:
M1= 5,972 10^24 kg (Massa della Terra)
r1= 6784 mt (distanza Stazione Spaziale e centro della Terra)
M2 = 450 10 ³ Kg (Massa Stazione Spaziale)
La sfera di Hill, nella sua versione più ottimistica, vale:
r2 = r1 (M2/M1)1/3
r2 = 6784 mt (450 10 ³ Kg/5,972 10^24 Kg)1/3
r2 = 6784 mt (75,35164^-21)1/3
r2 = 6784 mt 4,22374^-7
r2 = 28653,878 ^-7 metri
r2 = 0,0028653878 metri = 2,865 millimetri
E questa è la stima ottimistica, infatti applicando il coefficiente (1/3)^1/3
r2 = 0,0028653878 (1/3)^1/3 = 0,0019867489 metri = 1,9867 millimetri
Anche usando un'astronauta molto sottile è difficile farlo entrare nella sfera di Hill della Stazione Spaziale.
Paolo
Acc, e non nel senso di accelerazione, nei dati il raggio della Terra mi si è rimpiccolito di un fattore 10³
In pratica l’ho indicato in metri invece che chilometri.
Quindi in realtà la sfera di Hill (se non ho toppato qualche altro calcolo) vale:
r2 = r1 (M2/M1)^1/3
r2 = 6784 10³ mt (450 10 ³ Kg/5,972 10^24 Kg)^1/3
r2 = 6784 10³ mt 4,2237438 10^-7
r2 = 28653,878 10^-4 mt
r2 = 2,8653878 metri
Applicando il coefficiente (1/3)^1/3
r2 = 2,8653878 (1/3)^1/3 = 1,9867489 metri = 1,9867 metri
Vabbè un’astronauta delle dimensioni di Brunetta dovrebbe starci tranquillamente nella sfera di Hill della Stazione spaziale.
Paolo
Bello giocare a calcolare la sfera di Hill della stazione spaziale

Con questo intervento volevo solo ricordare che esistono comunque fattori di disturbo alle orbite nella sfera di Hill da tener comunque presente specialmente in oggetti di ridotte dimensioni e specialmente asimmetrici mi riferisco all'effetto Yorp - Yarkovsky .
https://it.wikipedia.org/wiki/Effetto_YORP
https://it.wikipedia.org/wiki/Effetto_Yarkovsky
Il mio intento con quanto scritto sopra è di mettere in evidenza l'instabilità orbitale di oggetti di piccole dimensioni che risentono maggiormente di questo effetto (diciamo di dimensioni dal kilometro in giù che tenderebbero col tempo ad orbite sempre più basse fino ad impattare con il corpo di massa gran lunga superiore questo spiegherebbe in parte l'assenza di tali satelliti in orbita nella zona interna del sistema solare.
Salve a tutti, complimenti per questo vostro "blog", veramente interessante e anche molto carino.
Per la sfera di Hill esiste questo calcolatore online semplice ed efficace, volevo segnalarvelo.
http://orbitsimulator.com/formulas/hillsphere.html
Ciao!
grazie Giovanni! anzi, un doppio grazie!!
La pagina di origine contiene altri calcolatori interessanti, alcuni non ho idea di cosa siano. Se non sono troppo complicati da spiegare ne puoi ricavare qualche articolo Enzo.
Thanks Giovanni.
caro Frank,
molti di quei problemi li abbiamo già affrontati... altri si basano su valori non ben conosciuti e altri sono relativi ad argomenti un po' troppo specifici. Dimmi tu se ne hai qualcuno che ti "intrippa" particolarmente.
Si ho visto, ma quel Kozai non l'ho mai sentito. Forse è più il nome che mi incuriosisce.
Ho trovato questo...
http://www.infinitoteatrodelcosmo.it/2015/01/16/pianeta-x-e-perche-no-anche-y/
uomo di poca fede...
Incredibile, avevo inserito nella ricerca "Kozai" ed era uscito inesistente.
Porc. mis. mo mi tocca leggerlo davvero....
Fatto, lo dicevo che quel nome incuriosisce..... Certo che te la sei cercata EnzoSamurai e quando sei andato in Giappone il film di Fantozzi con la scena di Pierugo era già storia (1975). Pensa se ti cucinavano l'amico iugoslavo e dovevi pure mangiarlo.
Noooooooooooo!! Sarebbe stato indigesto! Ricordo che quando sono andato a trovarlo a Belgrado, mi ha portato da alcuni amici. Abbiamo cominciato a mangiare alle 10 di mattina e abbiamo finito alle 5 del pomeriggio. Oltretutto, fin dall'inizio, il tutto era accompagnato dalla loro grappa di prugne (Slivovtza o qualcosa del genere). Roba da uccidere anche un samurai!
Caro Frank,
quando vuoi sapere se quel vulcanico astrofisico in pensione ha scritto qualcosa su qualche argomento (di solito lo ha fatto, credimi!), ti sconsiglio di usare il limitato motore di ricerca del blog, ma scrivi le parole chiave seguite da "zappalà" su google e vedrai...
Come credi che sia riuscito a scoprire tutti i suoi scheletri nell'armadio che ho raccontato qui http://www.infinitoteatrodelcosmo.it/tag/storia-di-vin-census/? Non penserai mica che me li abbia svelati lui??