Categorie: Relatività
Tags: dinamica relativistica energia invariante energetico Lorentz massa massa relativistica quantità di moto relatività ristretta velocità
Scritto da: Vincenzo Zappalà
Commenti:17
La Dinamica Relativistica ***
Questo articolo è stato inserito nella sezione d'archivio dedicata alla Relatività Ristretta, in Relatività, velocità della luce e buchi neri.
Questo lungo articolo mette insieme tutti quelli apparsi sulla Dinamica Relativistica. In particolare, mostra come si arriva "facilmente" alla più celebre formula dalle Fisica e ci dà un'idea di quanto la Relatività Ristretta sia necessaria alla Meccanica Quantistica. Chiudiamo un altro pezzo fondamentale della fisica moderna, prima di affrontare la Relatività Generale.
Le leggi newtoniane devono cambiare
I principi della RR ci hanno mostrato tante cose, ma, in particolare, ci hanno fatto capire che spazio e tempo sono strettamente legati tra loro e che, per passare dalle coordinate di un sistema di riferimento inerziale a quelle di un altro, è necessaria l’applicazione della trasformazione di Lorentz. Per velocità relative piuttosto piccole, la relatività galileiana è ancora valida, ma essa diventa inapplicabile quando la velocità si avvicina al valore c della luce.
Uno dei risultati fondamentali, in questo contesto, è che la velocità di un corpo misurata in un sistema di riferimento è legata a quella misurata in un altro sistema, e a quella del moto relativo dei due sistemi, attraverso una formula più complicata di una banale somma. La semplice addizione della teoria galileiana non vale più. Già questa conclusione ci fa capire che una sorte analoga devono subire altre grandezze fisiche di importanza fondamentale che “utilizzano” la velocità, come la quantità di moto e l’energia.
Basterebbe, comunque, prendere in esame la seconda legge della dinamica di Newton, la ben nota:
F = ma
Bene, immaginiamo che la forza sia costante. Ciò vuole anche dire che l’accelerazione è costante. Ne segue che la velocità cresce linearmente con il tempo. Sì… ma fino a quando? Basterebbe disegnare il solito grafico della velocità in funzione del tempo, quello stesso che ci è servito per introdurre le aree e gli integrali, e troveremmo una bella retta. Una retta, però, ci dice, tra le tante cose, che per t che tende a infinito anche la velocità tende a infinito.
No, c’è qualcosa che non va! Che il tempo sia anche grande poco importa, ma non possiamo accettare che la velocità cresca come vuole, dato che essa deve avere un limite dato dalla velocità della luce, c. Senza entrare ancora nei dettagli, possiamo concludere che la F = ma deve sicuramente essere modificata.
Introducendo il secondo principio della dinamica abbiamo automaticamente introdotto anche l’accelerazione. No, non saltate sulla sedia: siamo sempre nel campo della RR. Una cosa è descrivere un moto accelerato all’interno di un sistema di riferimento, e vedere come appare in un qualsiasi altro sistema inerziale, e un’altra è accelerare un sistema rispetto a un altro. Il secondo caso fa parte della Relatività Generale, ma il primo è ancora di dominio della RR. Essa non vieta certo a un corpo di accelerare e di muoversi a piacimento secondo le leggi della dinamica.
Normalmente, si pensa che il punto di arrivo più esaltante della dinamica relativistica sia la celeberrima formula E = mc2. E’ sicuramente “quasi” vero, anche se scritta in questo modo non dà piena ragione del suo significato generale. Ve ne sono, però, anche di più fondamentali, come quella che lega energia e quantità di moto e che, in qualche modo, ha portato al mare di Dirac (ed è anche un invariante!). Fermiamoci subito. Ci mancherebbe altro. Non è ancora tempo… L’accenno serve solo a far capire come per arrivare a descrivere qualcosa di interesse enorme e innovativo è necessario salire lentamente tutti gli scalini. Saltarne qualcuno può facilmente portare a una caduta disastrosa.
Noi faremo di tutto per arrivare “intuitivamente” alla formula più celebre della fisica (e non solo), ma per farlo ci sono molti modi. Purtroppo, leggendo nel web mi sono accorto che spesso e volentieri alcuni approcci creano più confusione che chiarezza. E’ quindi mia intenzione cercare di usare un approccio che parta proprio dall'inizio, seguendo, più o meno, proprio la logica di Einstein.
L’inizio più corretto è quello di dedicarsi alla legge della conservazione della quantità di moto. Già questo pone varie alternative che prendono in considerazione urti elastici o anelastici. Cambia poco, in realtà, a parte il numero di passaggi matematici (necessari, però, in qualsiasi approccio).
Ovviamente, faremo ricorso alla trasformazione di Lorentz e alla composizione delle velocità. Sarà perciò fondamentale ripassare le basi della RR, dato che non è pensabile introdurre di nuovo le dimostrazioni che hanno portato a certe formule ormai assodate. Esse saranno prese per buone e si rimanderà a dove sono state dedotte per saperne di più. Una piccola fatica che, però, non può essere evitata. Basta non avere fretta e non cercare di saltare in avanti, altrimenti la celebre formula rimarrà una specie di atto di fede (e noi questo NON lo vogliamo sicuramente).
In questo viaggio di avvicinamento ci scontreremo con la cosiddetta massa relativistica, gioia e dolore di tante elucubrazioni. Considerarla come a massa tutti gli effetti è sicuramente comodo e lo faremo anche noi, ma dovrà essere compreso bene il vero significato dell’intera faccenda.
Riguardo alla E = mc2, lasciatemi fare una piccola considerazione, che nessuno esprime mai apertamente, ma che molti, penso, facciano tra sé e sé. Noi abbiamo già dalla fisica classica una relazione ben conosciuta tra energia e massa di un corpo. Non è altro che l’energia cinetica K che vale.
K = ½ mv2
In fondo, anch’essa dice che l’energia è legata alla massa. Se la velocità fosse costante, utilizzando una congrua unità di misura, avremmo un’uguaglianza tra massa ed energia. Cosa c’è, allora, di così fondamentale e innovativo nella formula di Einstein, rispetto a quest’ultima?
Basterebbe dire che nel caso di una velocità uguale a zero, andrebbe a zero anche l’energia cinetica, indipendentemente dalla massa del corpo. Nella formula della RR, invece, l’energia espressa è del tutto indipendente dalla velocità (c è una costante per definizione) ed è valida anche quando la velocità intrinseca è ZERO. In altre parole, essa diventa un’energia che il corpo possiede anche quando è in quiete. Un’energia che dipende, perciò solo dalla massa: se “cambia” una deve cambiare anche l’altra! Un modo molto rozzo per valutare la rivoluzione che la formula porta con sé. Essa, in pratica, unisce due leggi fondamentali di conservazione: quella dell’energia e quella della massa, separate nella fisica galileiana.
Tuttavia, quella strana somiglianza tra ½ mv2 e mc2 è tutt’altro che casuale. Basterebbe pensare che l’energia cinetica, essendo legata alla velocità di un corpo, deve subire una trasformazione relativistica. Sarà facile vedere, quindi, come si passi da una all’altra a seconda della velocità in gioco. Ricordiamoci, infatti, che la dinamica relativistica, così come tutta la RR, è necessaria solo per velocità prossime a quella della luce. Qualsiasi legge si riesca a modificare, essa deve ricadere in quella corrispondente di Newton per piccole velocità.
Tutta questa chiacchierata per cosa? Forse per farvi venire voglia di non perdervi il ghiotto pasto che seguirà (a tempo debito) a questo antipasto (volutamente un po’ ambiguo e vago).
Non solo, però. Nei vari passaggi matematici si farà uso di qualche semplice integrale e di un semplicissimo sviluppo in serie. Niente di trascendentale, che poteva anche accettarsi senza entrare più di tanto nel merito. Ormai, però, mi conoscete: non voglio dare niente come atto di fede. Chi non vuole seguire la descrizione completa può anche farlo, ma deve essere una sua scelta. E’ mio dovere, perciò, permettervi di preparare il bagaglio completo necessario al viaggio nel meraviglioso mondo della RR (un vero capolavoro artistico e concettuale). Oltretutto, i maledetti integrali (e di conseguenza anche gli sviluppi in serie) sono estremamente amati dall’Universo per farsi descrivere attraverso la logica matematica…
Componiamo le velocità
Iniziamo la trattazione della Dinamica relativistica (DR) attraverso un piccolo quiz che ci permetta di vedere se abbiamo digerito bene le nozioni più importanti e necessarie della RR. Consideriamolo un utile ripasso.
Il problema è molto semplice…
Noi, osservatori, stiamo in un sistema di riferimento S (a due coordinate x e y). Un sistema di riferimento S’ si muove rispetto a noi con velocità v verso destra lungo l’asse x (x positive), come schematizzato in Fig. 1. Tutto ciò che è visto dal sistema S’ ha l’apice e tutto che ciò è visto da S non ha l’apice.
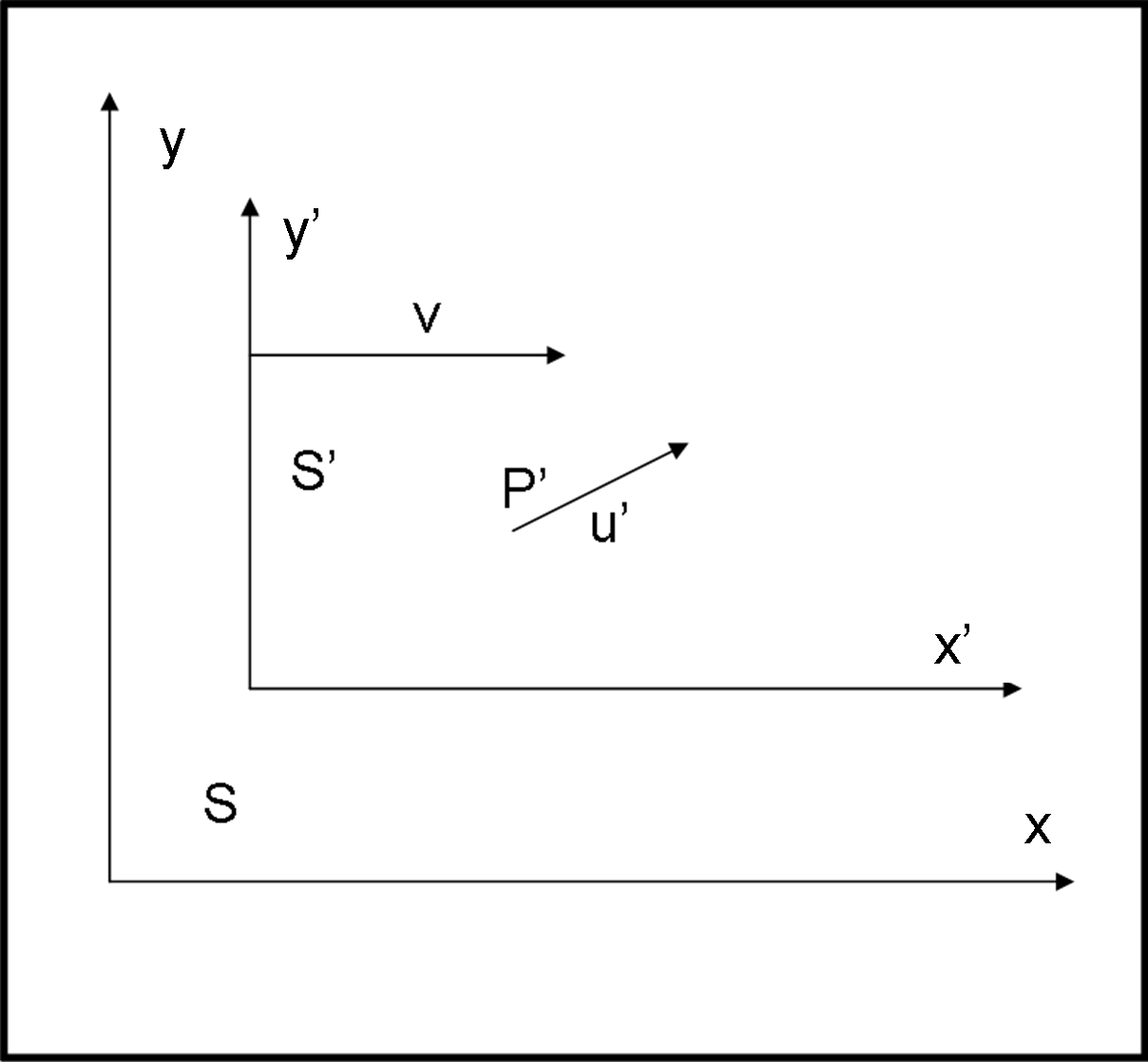
Immaginiamo, adesso, che un oggetto P’ si muova nel sistema S’ con una certa velocità u'.
Proponiamo tre casi:
(1) Il corpo P' si muove solo parallelamente all’asse x’, verso destra, con velocità u’x parallela a v.
(2) Il corpo si muove solo parallelamente all’asse y’, verso l’alto, (y' positive) con una velocità u’y, ortogonale a v.
(3) Il corpo si muove in diagonale con una certa velocità u’, tale che le sue componenti lungo x’ e y’ siano proprio u’x e u’y.
Per ogni caso, calcoliamo la velocità del corpo P’ vista da S, ossia ux, uy e u sia nel caso della relatività galileiana, sia nel caso della relatività ristretta.
Se volete, per rendervi conto praticamente delle contrazioni e/o estensioni, potete anche inserire dei valori numerici (considerate pure c = 1).
Particolare importanza, nel caso relativistico, è riflettere sulle differenze tra le componenti uy, nei tre casi. Esse sono le più importanti per la determinazione della quantità di moto relativistica.
Soluzione
Prima di iniziare, ribadiamo un paio di concetti che ormai dovrebbero essere ben digeriti. Tuttavia, benché digeriti, è utile, comunque, sintetizzarli per cominciare al meglio il cammino verso la dinamica relativistica. La loro trattazione completa si trova, comunque, QUI e QUI. Sto parlando, ovviamente, della combinazione relativistica delle velocità.
Immaginiamo, in Fig. 2, un sistema S’ (una nave interstellare con il suo capitano) che si muove rispetto a noi alla velocità v diretta secondo l'asse x. All’interno della nave vi è un oggetto P’ che si muove con velocità u' = u’x nella stessa direzione dell’astronave. Notate l’uso dell’apice.
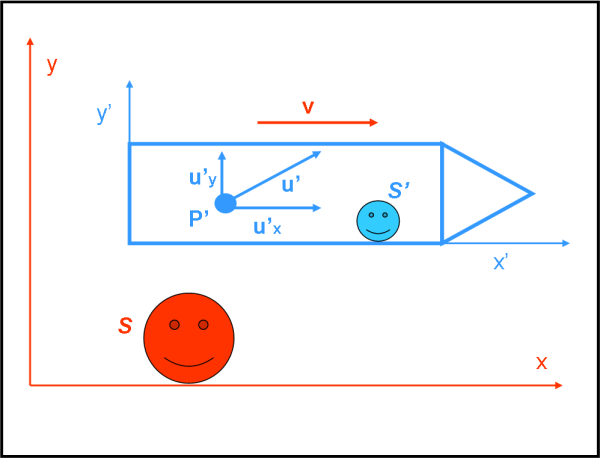
La velocità v è qualcosa di cui ci accorgiamo noi e quindi è senza apice (sistema di S). La velocità u’x è un qualcosa di cui si accorge il capitano (S’) e quindi deve avere l’apice. Ciò vuole dire che, per il capitano che crede di essere fermo, l’oggetto P’ si muove solo secondo u’x. Ci chiediamo: “A quale velocità viene visto viaggiare l’oggetto P’ da noi, S, ossia qual è la sua velocità ux senza apice (essendo misurata nel sistema S)?” Se rispondesse Galileo ci direbbe:
ux = v + u’x.
Se fosse realmente così, però, la somma v + u’x potrebbe diventare tranquillamente più grande di quella della luce. Ne segue che, in campo relativistico, bisogna evitare che ciò accada. Deve esistere una trasformazione tra chi sta fermo e tra chi si muove, che permetta di non correre questo rischio. E così cadiamo nelle trasformazioni di Lorentz. Applicandole correttamente, si trova che la somma galileiana delle velocità può ancora andar bene fino a che stiamo trattando con velocità molto basse, dopo di che la formula si complica e ci porta a eseguire la somma, tenendo conto di certi fattori di correzione.
ux = (v + u’x)/(1 + vu’x/c2) …. (1)
Il denominatore è una quantità sicuramente maggiore di uno, da cui segue che la velocità orizzontale finale è sicuramente più piccola della somma delle due velocità. Anche se imponessimo che sia v che u’x siano uguali alla velocità della luce, otterremmo un valore finale ux = 2c/(1 + 1) = c. Einstein ci sapeva fare...
Fin qui abbiamo trattato una composizione di velocità che hanno la stessa direzione. Vi dico subito che nel prosieguo questa componente ci interesserà ben poco, ma è sempre meglio averla sott’occhio.
Molto più interessante è il caso in cui la velocità u’ sia diretta in modo qualsiasi (ragioniamo comunque sempre su un piano e quindi con una componente x e una y). Per lavorare con sicurezza e chiarezza è necessario scomporre la velocità u’ nelle sue due componenti: una nella direzione del moto dell’astronave rispetto a noi (u’x parallela a v, come nel caso precedente) e una in direzione ortogonale (u’y) .
Per Galileo la velocità vista da S porterebbe a:
ux = u’x + v
e
uy = uy’
e niente, in fondo, cambierebbe, dato che la componente lungo x è già stata trattata prima, mentre quella ortogonale rimarrebbe immutata. Ne segue che la velocità totale vista da S si ottiene sommando i vettori ux e uy = uy’ (il modulo u si determina attraverso il banale teorema di Pitagora)
Nel caso relativistico le cose si complicano. Diciamolo prima a parole e poi passiamo alle formule.
La componente ux viene descritta dalla (1) ed è già stata risolta. Non dimentichiamo, comunque, che essa esiste e dovrà poi essere tenuta in conto! Cosa succede alla componente uy?
In altre parole, come si trasforma la componente della velocità u’ secondo y’ (com'è vista da S’), quando viene vista dal sistema S. Essa deve perdere l’indice e diventare una uy.
La risposta potrebbe sembrare ovvia: “Sappiamo che, anche nella RR, y = y’ (trasformazioni di Lorentz) e, quindi, anche le componenti delle velocità relative a questi assi devono rimanere uguali come succede per Galileo”. No, assolutamente no! Una velocità è data dal rapporto tra una lunghezza e un tempo e se è vero che le lunghezze secondo y si mantengono non è affatto vero che il tempo di S’ visto da S si mantenga. Anzi, sappiamo benissimo che cambia e come! Il che vuol dire che deve cambiare anche la componente della velocità ortogonale alla direzione del moto relativo dei due sistemi.
Consideriamo il caso più generale, ossia quello in cui stiamo proprio parlando di una componente di una velocità u’, diretta comunque, e separata nelle sue due componenti.
La velocità ortogonale u’y, vista da S diventa una uy , data dalla formula
uy = u’y (1 – v2/c2)1/2/(1 + v u’x/c2) …. (2)
Non dobbiamo certo stupirci che compaia la velocità v e la componente u’x (d’altra parte basta ricordare che tempo e coordinata x sono strettamente collegati… se cambia il primo deve cambiare anche la seconda, come ci dicono sempre le trasformazioni di Lorentz).
Tuttavia, la formula si semplifica non poco se la velocità u’ di P’ è diretta SOLO in direzione ortogonale, rispetto al moto di S’. In questo caso u’ coincide con u’y e abbiamo immediatamente che u’x = 0. La formula di prima si trasforma nella più semplice e intuitiva:
uy = u’y (1 – v2/c2)1/2 …. (3)
In parole povere, dato che il termine sotto radice quadrata è sempre minore di uno, la componente ortogonale della velocità dell’oggetto P’, lanciato all’interno dell’astronave ortogonalmente al moto dell’astronave, viene vista accorciarsi da S, rispetto a quella u’y che vede il capitano in S’. E più la velocità dell’astronave è grande è più la componente ortogonale della velocità dell’oggetto P’, visto dal papallo S, appare diminuire. Tuttavia, stiamo ben attenti che la velocità totale vista da S è qualcosa di ben diverso, dato che l’astronave continua a viaggiare sempre a velocità v.
Abbiamo visto che, sia per una velocità con direzione qualsiasi che per una velocità soltanto ortogonale dell’oggetto P’, la componente della velocità uy vista da S si riduce rispetto a quella u’y vista da S’. Nel caso che la velocità abbia direzione qualsiasi, questa riduzione è regolata da due fattori di correzione (2): uno è relativo solo alla velocità del’astronave v ed è dato da (1 – v2/c2)1/2 e l’altro anche dalla componente della velocità di P’ lungo x’ (u’x) ed è dato da 1/(1 + v u’x/c2) . Nel caso che la velocità di P’ sia solo diretta lungo l’asse y’ (3), il fattore di correzione si riduce solo al primo, ossia a (1 – v2/c2)1/2. L’altro, ovviamente, si riduce a 1, dato che u’x = 0.
La componente ux, se esiste u’x, segue sempre la contrazione relativistica data dalla (1). Se u’x è uguale azero, ux si riduce alla velocità v tra i due sistemi.
Per darne una visione grafica completa ci possiamo riferire alla Fig. 3, in cui tutto ciò che è visto dal sistema S’ è rappresentato in blu (con l’apice), mentre ciò che è visto da S è rappresentato in rosso (senza apice). Teniamo presente che le contrazioni dei vari vettori sono state introdotte “a caso” e non corrispondono a una qualche scelta particolare delle velocità. Insomma, la figura è solo qualitativa, almeno per quanto riguarda la parte relativa a Einstein (RR). Ovviamente, la velocità v relativa alla parte sinistra deve essere decisamente più piccola della v della parte destra!

Con queste nozioni acquisite, siamo in grado di affrontare la dinamica relativistica e vedere come le assunzioni della RR stravolgano la dinamica newtoniana, sempre e soltanto se le velocità si avvicinano di molto a quella della luce.
Conserviamo e non uguagliamo
Riassumiamo e fermiamoci a pensare al concetto che sta alla base di tutta questa rivoluzione. Ciò che la cinematica relativistica ha voluto fare è, in fondo, solo e soltanto non permettere che qualcosa possa superare la velocità della luce. Per far ciò è stato necessario allungare tempi e accorciare lunghezze e, per quanto ci interessa d’ora in poi, accorciare le velocità ortogonali alla direzione del moto. Il punto chiave di tutto è proprio questa conclusione.
Basterebbe solo quest’ultimo concetto per dimostrare in modo quasi immediato che sotto l’ipotesi della RR la quantità di moto, la “mia” grandezza preferita (la lumachina della Fisica Addormentata nel Bosco…), non può più essere definita con la formula newtoniana che dice:
q = mv
Se mantenessimo questa definizione, la RR ci porterebbe alla sua NON conservazione, uno dei capisaldi di tutta la fisica, che nemmeno Einstein ha intenzione di distruggere. Non ci resta che dimostrare la sua non conservazione e correre ai ripari.
Dimostrare la non conservazione della quantità di moto definita con la fisica classica, ma immersa nel mondo relativistico, non è gioco banale come potrebbe sembrare a prima vista. Cosa altrettanto non immediata è verificare che una nuova definizione della quantità di moto la conservi anche in campo relativistico. Diffidiamo di tentativi semplificati che mischiano capra e cavoli.
Ciò che è importante capire molto bene è che siamo costretti a cambiare la definizione di quantità di moto, ossia da q = mv (definizione classica) dobbiamo passare a qualcosa del tipo qR = m'v, dove m’ si possa considerare una variabile che cresca con la velocità a cui viaggia il corpo visto da un qualsiasi sistema di riferimento inerziale.
Non vogliamo assolutamente uguagliare la quantità di moto classica con quella relativistica, ma dimostrare che quella relativistica si conserva e che solo per velocità molto basse coincide con quella classica.
Niente metodi semplificati, quindi, ma affrontiamo, senza esitazioni, un esperimento leggermente più complesso, che risulta del tutto ovvio, emozionante e appagante, se seguito con grande attenzione e molta calma. D’altra parte, chi è interessato a entrare nel mondo sconvolgente e rivoluzionario della dinamica relativistica, nel mondo in cui energia e massa si abbracciano strettamente come indica (solo parzialmente) la celebre formula di Einstein, nel mondo che è poi quello che ci circonda (le scuole prima o poi lo capiranno?), non può esimersi dall’accettare un piccolo sforzo.
Abbiamo cercato, al pari del tempo relativistico, di fare scorrere i vari passaggi con molta lentezza, quasi al rallentatore, invitando a fermarsi a riflettere nei punti più critici. Infondo, è solo necessario comprendere il concetto logico dei vari passaggi, dato che la matematica è veramente ridicola e alla portata di qualsiasi studente (forse anche di scuola media, se ricordo bene). Siamo anche sicuri che, fatti i dovuti arrangiamenti, l’intera problematica possa essere anche spiegata a livello papalliano…
Nessuna paura, quindi, dato che le difficoltà sono alla portata di tutti coloro che abbiano voglia di imparare e che abbiano digerito, più o meno, la cinematica della Relatività Ristretta (RR).
Due palline e un urto elastico galileiano
Iniziamo a descrivere un esperimento relativo a un urto elastico tra due corpi. In questo tipo di fenomeno, la quantità di moto dà il meglio di sé. Cerchiamo di stare bene attenti ai colori delle varie frecce e delle componenti delle velocità che compariranno nelle figure. Nel testo aggiungeremo qualche indice per supplire ai colori, ma l’importante è mantenere una visione unitaria.
Tutto ciò che si riferisce a un sistema di riferimento S’ viene segnato in blu, tutto ciò che si riferisce a un sistema di riferimento S viene segnato in rosso. Ciò che succede lo vediamo da S. Il che vuol dire che tutte le componenti delle velocità di S’ devono, comunque, essere disegnate in rosso, dato che sono quelle di S’ viste da S. All’inizio tutte queste parole sembrano inutili (e lo sono, in effetti), ma, introducendo la RR, le cose cambiano e non dobbiamo farci prendere in contropiede.
Un solo sistema di riferimento
Questa prima parte la vediamo descritta nella Fig. 4.
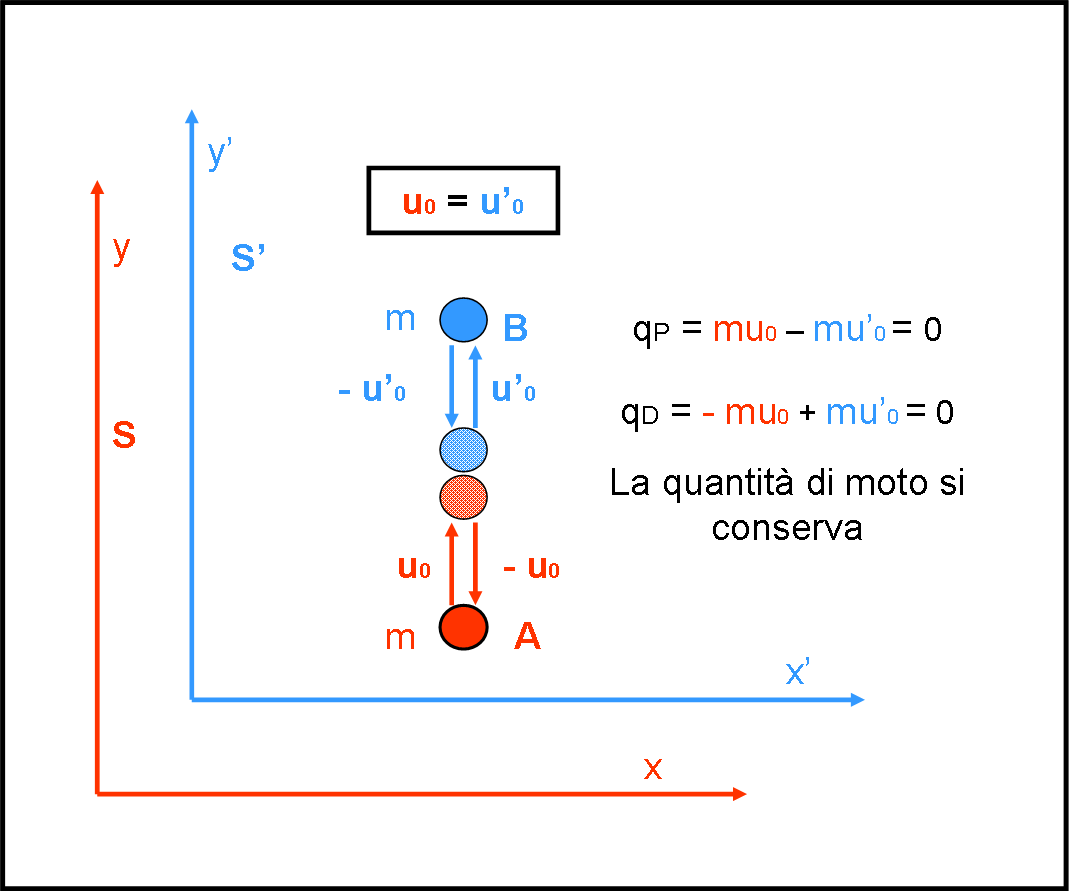
Due palline A (rossa) e B(blu) hanno la stessa massa m. A appartiene al sistema di riferimento S e B al sistema di riferimento S’. I due sistemi sono fermi uno rispetto all’altro. I due osservatori lanciano le loro palline lungo gli assi y e y’ (coincidenti), con la stessa velocità di modulo u0. Le due palline si urtano nel punto di mezzo.
La quantità di moto è un vettore, ma noi trattiamo d'ora in poi con le sue componenti lungo gli assi e, quindi, possiamo limitarci ai moduli. Ogni pallina ha una certa quantità di moto: A ha una quantità di moto mu0 e B ha una quantità di moto – mu0. Inseriamo i pedici P e D per distinguere la quantità di moto Prima e Dopo l'urto. Il sistema delle due palline ha quindi, prima dell’urto, un momento totale della quantità di moto dato da:
qP = mu0 – mu0 = 0
Dopo l’urto (perfettamente elastico), le palline invertono la loro velocità, per cui la pallina A acquista una quantità di moto – mu0, mentre la pallina B acquista una quantità di moto mu0. La quantità di moto del sistema dopo l’urto diventa:
qD = – mu0 + mu0 = 0.
Possiamo concludere che la quantità di moto si è conservata. Tutto secondo le previsioni, dato che il sistema è isolato e non vi sono forze esterne a disturbarlo.
Qualche considerazione sui colori…
Le frecce viste da S’ sono blu, le frecce viste da S sono rosse. I due sistemi sono fermi e, quindi, i colori possono essere tranquillamente scambiati o essere considerati uguali. In fondo, il sistema di riferimento è uno solo poiché S = S’. Analogamente, è del tutto equivalente scrivere u’0 o u0, dato che anche loro sono uguali. Guardiamo bene la figura precedente e cerchiamo di capire perfettamente la possibilità di scambiare u0 con u’0 e i loro colori.
S’ si muove lentamente, seguendo Galileo
Mettiamo, adesso, in movimento il sistema S’ con una certa velocità v di trascinamento rispetto a S lungo l’asse x (ossia facciamo scorrere l’asse x’ lungo x con una velocità v), come descritto in Fig. 5. La velocità v non ha apice e viene colorata in rosso, dato che viene “vista” solo da S.
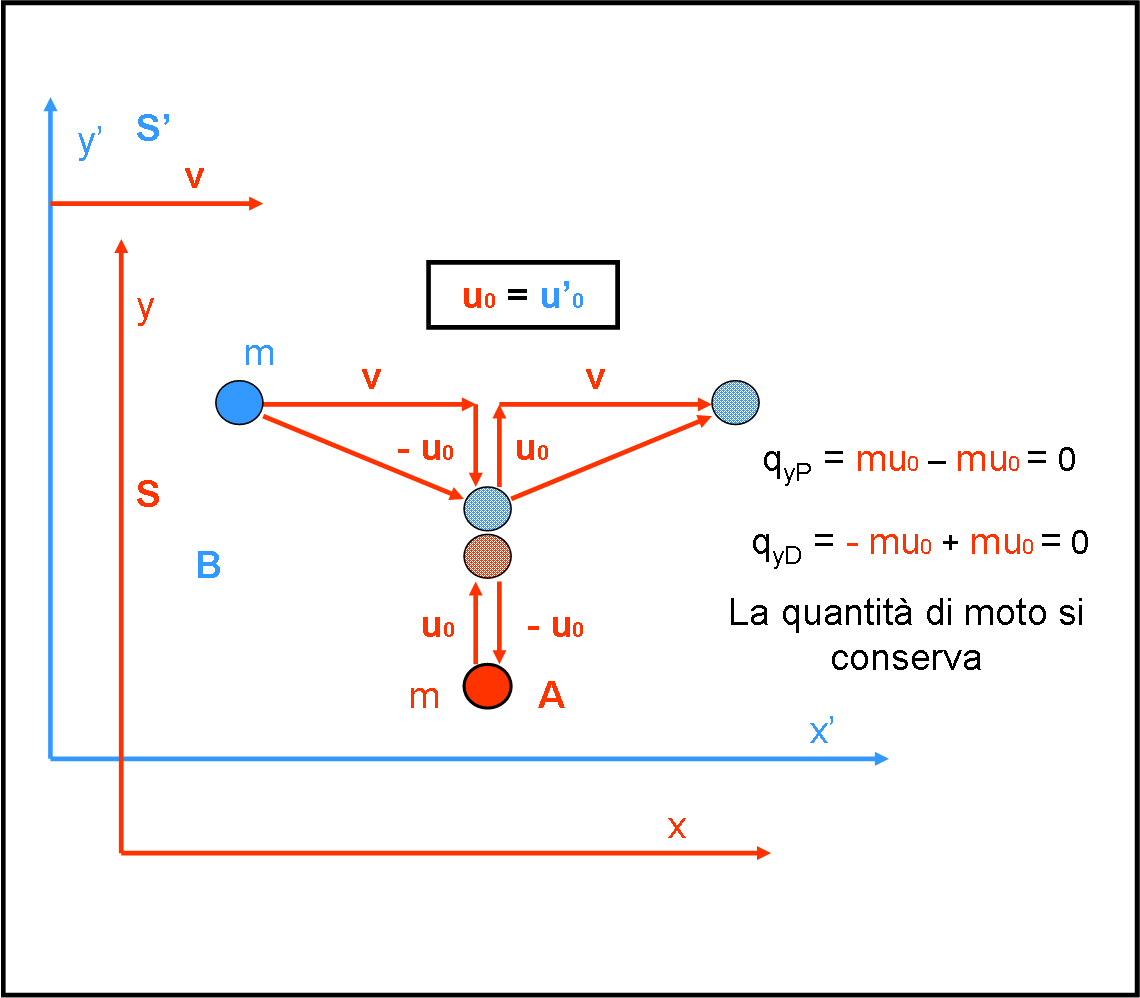
Osserviamo, come sempre, lo svolgimento dell’esperimento dal riferimento S. Le cose, in ambito galileiano, non cambiano. La velocità u0 rimane la stessa di prima (u0 = u’0), vista da entrambi i sistemi. Tuttavia, coloriamo in rosso anche la velocità relativa alla pallina B di S’, dato che la stiamo vedendo da S. La perfetta uguaglianza dipende dal fatto che per Galileo le velocità ortogonali al movimento tra i due sistemi non vengono assolutamente influenzate.
Le due palline si urtano come prima, anche se S continua a vedere A andare verso l’alto e poi tornare verso il basso, mentre la B di S’ è vista percorrere una linea spezzata, data dalla composizione della velocità di trascinamento v dei due sistemi e della velocità u0 = u0’ della pallina. Comprendiamo bene questa figura, mi raccomando. La pallina B viene lanciata in S’, ma prima che arrivi a urtare la A, lanciata in S, deve viaggiare anche in senso orizzontale con velocità v.
Ovviamente, la faccenda, se vista da B in S’, sarebbe perfettamente simmetrica. Per S’ sarebbe S che si muove con velocità – v, ma la conclusione sarebbe la stessa, anche se invertita. Nessun problema, quindi, a lavorare solo su S.
Possiamo concludere che, anche con il sistema S’ in movimento, la quantità di moto delle palline rimane inalterato, dato che sia le masse che le velocità sono rimaste identiche. La quantità di moto si conserva nell’urto.
In realtà, abbiamo considerato solo la componente verticale della quantità di moto totale (la quantità di moto è un vettore, non dimentichiamolo). Dovevamo considerare anche quella orizzontale? Teoricamente sì, ma questa si mantiene e si manterrà sempre. Possiamo anche dimostralo facilmente.
Prima dell’urto, essa vale:
qPx = 0 + mv
La quantità di moto della pallina rossa per il sistema S è ovviamente ZERO, dato che la pallina non si muove lungo l’asse orizzontale. La quantità di moto orizzontale della pallina blu, vista da S, è data da mv.
Dopo l’urto, essa vale:
qDx = 0 + mv
Nulla è cambiato, dato che, sebbene la pallina A inverta il suo moto, essa continua a muoversi solo secondo l’asse y: la sua componente orizzontale rimane ZERO. La pallina blu, invece, continua a viaggiare, rispetto a S, con velocità v nella stessa direzione di prima.
Notiamo, già adesso, che questa componente non interessa nemmeno se si applica la RR. Anche in quel caso la velocità orizzontale della pallina rimane sempre v (la velocità di trascinamento vista da S). Non esiste una composizione di velocità orizzontale. In altre parole, la componente orizzontale può sempre essere trascurata e ci si può dedicare solo e soltanto alla componente verticale. Fermiamoci un attimo e pensiamo a questa conclusione: essa DEVE apparire del tutto logica.
La velocità diventa relativistica
Immaginiamo adesso di applicare la RR al secondo caso (applicarla al primo non avrebbe senso dato che non vi è movimento relativo). Respiriamo a lungo, riassumiamo mentalmente ciò che abbiamo acquisito e… proseguiamo. Non dimentichiamo che tutte le velocità osservate dal sistema S’ rimangono sempre uguali a quelle disegnate nella Fig. 5. Il sistema S’ non si sente assolutamente diverso. Sono le sue velocità viste da S che cambiano a causa del moto di S’. Queste velocità viste da S sono, perciò, colorate in rosso. Rappresentiamo il fenomeno (che deve risultare sempre lo stesso dato che qualsiasi fenomeno fisico deve rimanere lo stesso in qualsiasi sistema inerziale) nella Fig. 6 che rimpiazza la Fig. 5.
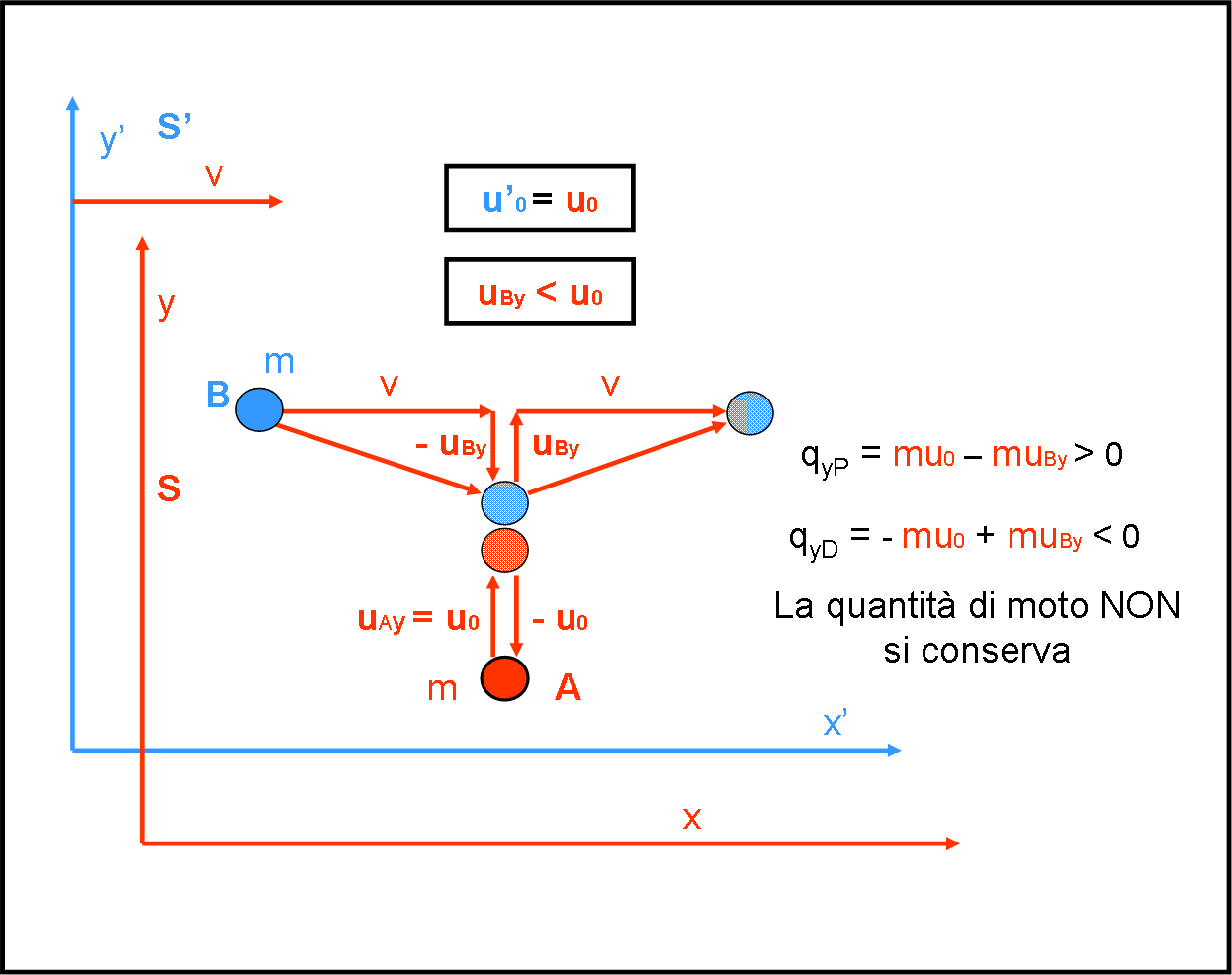
A prima vista potremmo pensare che non è cambiato niente. E, invece, qualcosa è cambiato. La v rimane la stessa dato che è quella che è e si riferisce a S (è solo lui che la “vede”), ma la componente verticale rossa della velocità della pallina blu vista da S (che chiamiamo per comodità uBy) è più piccola di quella del caso precedente. Non dobbiamo certo stupirci, dato che la velocità ortogonale alla direzione del moto, subisce un accorciamento come ricordato fin dall’inizio.
Possiamo riscrivere la formula (2) per la componente prima dell’urto:
- uBy = - u’By (1 – v2/c2)1/2/(1 + v u’Bx/c2)
Abbiamo solo cambiato gli indici (e il segno), per applicarla al nostro esperimento.
Anche se non possiamo eseguirlo praticamente nel testo, pensiamo che le componenti che hanno l’apice si riferiscono al sistema S’ e dovrebbero essere scritte in blu.
Tuttavia, possiamo eseguire delle semplificazioni. u’By non è altro che uBy, la componente della pallina blu vista da S, ossia l’originale u0. Nel sistema di riferimento S’ la velocità è sempre la stessa. Inoltre, u’Bx non è altro che la componente orizzontale della velocità u0 vista da S’. Ma questa è ZERO, dato che la pallina blu in S’ non si muove assolutamente in orizzontale!
La formula di prima si trasforma nella (3) che, applicata al nostro caso, come dovevamo aspettarci, dà:
- uBy = - u0(1 – v2/c2)1/2 …. (4)
Non ci resta che calcolare la componente verticale della quantità di moto totale qP, prima dell’urto. Per analogia, la velocità della pallina A (rossa) può anche essere scritta uAy, pur sapendo che essa vale sempre u0.
Quella della pallina rossa (A), rimane sempre la stessa, ossia muAy = mu0. Quella della pallina blu vista dal sistema S deve fare uso della (4). In conclusione abbiamo:
qPy = muAy - muBy = mu0 - m u0 (1 – v2/c2)1/2 > 0
Notiamo, infatti, che la seconda parte è SICURAMENTE più piccola della prima parte, dato che la stessa quantità è stata moltiplicata per un numero minore di uno (la radice quadrata).
Calcoliamo, adesso, la componente verticale della quantità di moto totale qD, dopo l’urto.
Per la pallina rossa, abbiamo - muAy = - mu0, per la pallina blu, abbiamo muBy (si ha completa simmetria prima e dopo l’urto), da cui:
qDy = - muAy + muBy = - mu0 + m u0 (1 – v2/c2)1/2 < 0
Per essere ultra pignoli e ripetitivi, stiamo aggiungendo, a una certa quantità negativa, la stessa quantità (positiva) moltiplicata per un numero minore di uno. Il risultato deve essere una quantità minore di ZERO.
Purtroppo, dobbiamo ammettere che la quantità di moto verticale non si conserva. D’altra parte sappiamo già che quella orizzontale si conserva e quindi non possiamo che concludere che la quantità di moto totale non si conserva nell’urto!
Cambiare o non cambiare? Questo è il problema…
Abbiamo di fronte una situazione imbarazzante e non banalissima… Potremmo scegliere una via d’uscita decisamente comoda: accettare il fatto che la quantità di moto non si conserva nella RR e … buonanotte a tutti! Tuttavia, la non conservazione della quantità di moto comporterebbe la non conservazione di molte altre grandezze. La fisica ne sarebbe stravolta…
No, siamo troppo seri per fare una cosa del genere e dobbiamo seguire quanto fatto, con grande ragionevolezza, da Einstein: dobbiamo proprio cambiare definizione dalla quantità di moto, in modo che:
1) Essa si conservi anche nella RR
2) Per velocità molto piccole coincida con la definizione classica
Abbiamo deciso di cambiare la definizione di quantità di moto. Dirlo è una bella cosa, ma farlo è un’altra. La soluzione migliore sembrerebbe quella di considerare la massa come una funzione della velocità. Non abbiamo certo detto una cosa da poco. Basterebbe pensare che ciò vuole dire che l’inerzia di un corpo cambia al variare della sua velocità. Teoricamente potrebbe diventare infinita. Non ci resta che fare questo tentativo e controllare, con molta attenzione, se questa sconvolgente ipotesi riesce, veramente, a conservare la nuova quantità di moto.
Cambiamo la quantità di moto
Bene, cominciamo a vedere qual è la velocità totale di entrambe le palline, quando vengono viste dal sistema S.
Consideriamo la Fig. 7 (uguale alla 6), ponendo particolare attenzione al triangolo indicato dalla freccia.
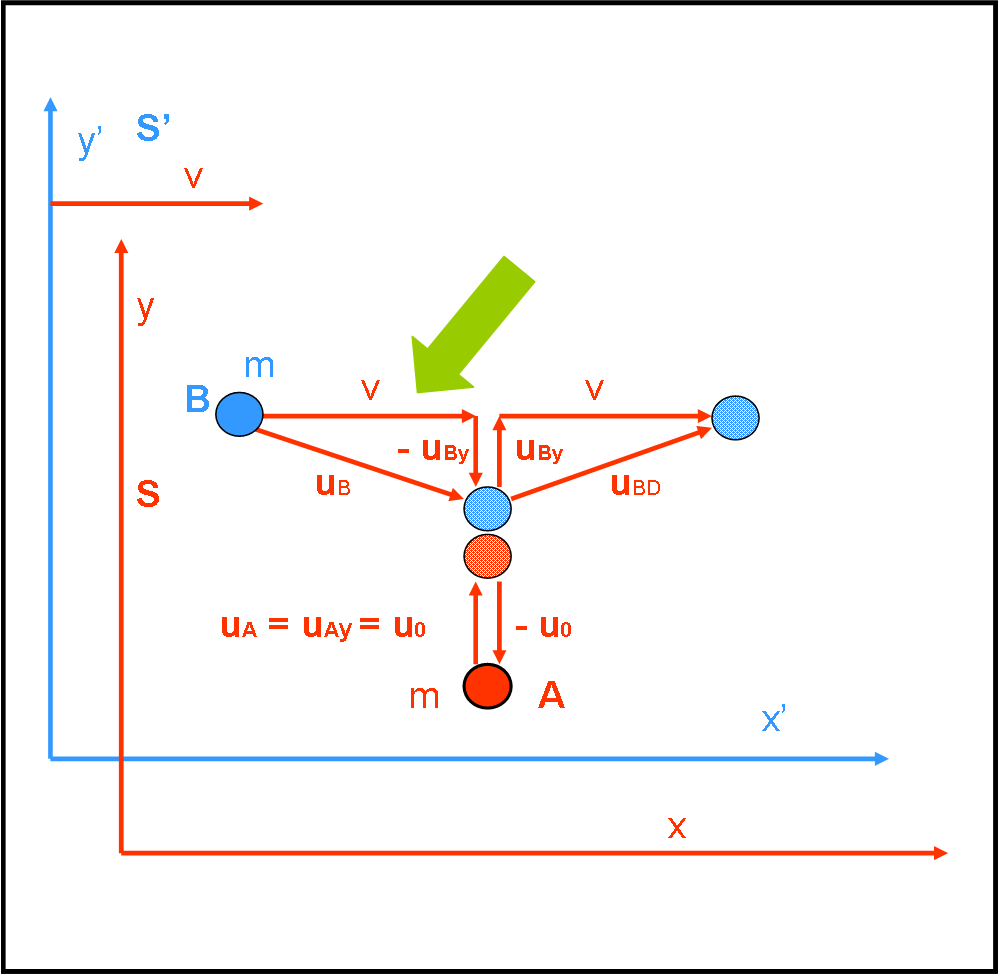
Attenzione! E’ cosa ben diversa da quella fatta finora, in cui ci siamo occupati solo della componente verticale, dato che era quella che decideva la conservazione oppure no della quantità di moto. Adesso, volendo cambiare la definizione della quantità di moto, facendo variare la massa in funzione della velocità di entrambe le palline, siamo obbligati a calcolare proprio queste velocità per poter cambiare la massa. Alla fine, torneremo di nuovo alla sola componente verticale che sarà però quella corretta.
Cominciamo con la parte più facile: la velocità uA della pallina rossa. Beh… essa rimane sempre la stessa, ossia:
uA = uAy = u0
Tocca adesso alla velocità uB della pallina blu vista sempre da S. Cominciamo a verificare se è veramente più grande di uA.
Essa altro non è che la composizione delle velocità lungo x e lungo y della pallina blu (teorema di Pitagora), viste da S, ossia:
uB2 = uBx2 + uBy2 = v2 + (- u0(1 – v2/c2)1/2)2 = v2 + u02(1 – v2/c2)
uB2 = v2 + u02 – u02 v2/c2 = u02 + v2(1 – u02/c2) > u20 = u2A
Risulta chiaro che uB è maggiore di uA
Ricordiamoci bene questo passaggio:
uB2 = v2 + u02 – u02 v2/c2 …. (5)
ci tornerà molto utile tra poco.
Definiamo ora una nuova massa tale che, in generale, valga:
mW = m0 /(1 – w2/c2)1/2
dove m0 è la massa a riposo, ossia quella relativa al corpo fermo, mentre mW è la massa quando il corpo si muove alla velocità w (quaslsiasi).
La nuova quantità di moto relativistica diventa, allora:
qR = mW w = m0w/(1 – w2/c2)1/2
Notiamo, nuovamente, che la massa dipende direttamente dalla velocità w dell’oggetto (il pedice si riferisce alla loro effettiva velocità vista da un certo sistema di riferimento)
Inseriamo le nuove masse nelle quantità di moto del nostro caso. Abbiamo (come al solito, il pedice P indica “prima dell’urto”):
qRPA = muAuA = m0uAy/(1 – uA2/c2)1/2 = m0u0/(1 – u02/c2)1/2
qRPB = muBuB = m0uB/(1 – uB2/c2)1/2
Tuttavia, a noi interessano solo le componenti verticali delle due quantità di moto relativistiche, ossia qRPAy e qRPBy.
Ricordiamo anche che qRPA = qRPAy.
qRPAy = m0uAy/(1 – uA2/c2)1/2 = m0u0/(1 – u02/c2)1/2
qRPBy = - m0uBy/(1 – uB2/c2)1/2
Notiamo bene quello che abbiamo fatto: la massa corretta è definita sulla base della velocità uB della pallina, ma la componente della velocità che stiamo considerando, per il calcolo della quantità di moto verticale, è solo quella verticale. Non confondiamoci, mi raccomando…
Possiamo anche scrivere (ricordando la (4)):
qRPBy = - m0uBy/(1 – uB2/c2)1/2 = - m0u0(1 – v2/c2)1/2/(1 – uB2/c2)1/2 …. (6)
Divertiamoci, adesso, con semplici passaggi algebrici… e niente paura, dato che basta seguirli passo dopo passo.
Partiamo dalla (5):
uB2 = v2 + u02 – u02 v2/c2
uB2/c2 = v2/c2 + u02 /c2 - u02 v2/c4
1 - uB2/c2 = 1 - v2/c2 - u02 /c2 + u02 v2/c4 = (1 - v2/c2) - (u02/c2)(1 - v2/c2) = (1 - v2/c2)(1 - u02 /c2)
(1 - uB2/c2)1/2 = (1 - v2/c2)1/2 (1 - u02 /c2)1/2
Nessun problema, vero? Abbiamo solo diviso per una stessa quantità, cambiato di segno e aggiunto il numero 1, messo in evidenza un fattore comune ed eseguita la radice quadrata.
Sostituendo nella (6), otteniamo:
qRPBy = - m0u0(1 – v2/c2)1/2/((1 - v2/c2)1/2 (1 - u02 /c2)1/2)
qRPBy = - m0u0/(1 - u02 /c2)1/2
Possiamo, finalmente, calcolare la componente verticale della quantità di moto totale prima dell’urto:
qRPAy + qRPBy = m0u0/(1 – u02/c2)1/2 - m0u0/(1 - u02 /c2)1/2 = 0
Fantastico, soprattutto perché dopo l’urto, tutto rimane simmetrico e vale ancora ZERO.
La quantità di moto si è conservata! La nuova quantità di moto relativistica qR funziona e possiamo proprio definirla, per una velocità w qualsiasi:
qR = m w = m0w/(1 – w2/c2)1/2
Non ci resta che provare che per velocità decisamente inferiori a quella della luce, la quantità di moto relativistica diventi quella classica, ossia:
Se w << c, allora qR = q
Beh… questa verifica è immediata
qR = m0w/(1 – w2/c2)1/2
Se w << c
Si ottiene:
qR = m0w = q
Per valori piccoli di u, la quantità di moto relativistica tende a coincidere con quella classica e compare soltanto la massa a riposo.
Concludendo: La quantità di moto relativistica si conserva in tutti i sistemi di riferimento inerziali e per valori piccoli della velocità tende a coincidere con la quantità di moto classica.
Un metodo alternativo
Chi vuole divertirsi ancora un po’ (è del tutto facoltativo) può arrivare alla stessa conclusione, utilizzando il ragionamento fatto da Feynman. E’ sicuramente un metodo più rapido, senza formule noiose, ma comporta un ragionamento finale sul risultato che potrebbe causare una qualche confusione nei meno attenti e concentrati. Sicuramente, è geniale come tutto ciò che ha fatto lui…
Attraverso un esperimento del tutto simile a quello usato da noi, Feynman dice, molto semplicemente, che si possono considerare per le due palline due masse diverse, a seconda delle loro velocità, e definire la quantità di moto relativistica, in generale, come:
qR = mW uW.
Nel nostro caso, le due masse e le loro due velocità sono muA e muB e uA e uB.
Tuttavia, si sa anche che la componente di uB nel verso verticale è - uA(1 – v2/c2)1/2
Ne segue che la componente della quantità di moto della pallina A, prima dell’urto, in senso verticale, è:
qAR = muAuA
e quella della pallina B è:
qBR = muBuB= - muBuA(1 – v2/c2)1/2
La quantità di moto totale verticale prima dell’urto deve essere (per la conservazione):
muAuA - muBuA(1 – v2/c2)1/2 = 0
Semplificando:
muB(1 – v2/c2)1/2 = muA …. (7)
A questo punto possiamo far tendere uA a zero (imporre alla pallina A una piccolissima velocità verticale). Facendo questo, la velocità uB tende a essere proprio la velocità v. Ne segue che la massa muA tende a diventare la massa a riposo m0 (velocità zero) e la massa muB tende a diventare la massa relativa alla velocità v, ossia mV. La (7) diventa:
mv = m0 /(1 – v2/c2)1/2
Che è proprio l’espressione della massa relativistica. Ne segue che applicando la massa relativistica si ottiene la conservazione della quantità di moto relativistica.
Perché non abbiamo usato solo questo approccio? Se non altro, perché manovrando con le componenti abbiamo preso maggiore dimestichezza con il concetto del problema. Un po' di esercizio non fa mai male. Più correttamente potremmo dire che il metodo di Feynman ha:
Un grande vantaggio: non ha bisogno di calcoli, ma solo di un paio di… limiti.
Un possibile svantaggio: potrebbe far pensare che quella che conta è solo la velocità tra i due sistemi (errore che si commette spesso). In questo caso, la velocità si riduce a v solo perché si elimina il moto verticale… La v è proprio la velocità TOTALE della pallina.
Ovviamente, il grande Richard, quando faceva divulgazione, era convinto di trovarsi di fronte la massima concentrazione e il massimo desiderio di imparare. Da una parte, il divulgatore ha l’obbligo di essere chiaro, preparato e di non parlare per mettersi in mostra, ma solo per insegnare. Dall’altra, chi ascolta, ha l’obbligo di dare il meglio di sé, con pari umiltà e passione.
La differenza tra i due metodi usati è veramente molto piccola, anche se concettualmente diversa. Nel primo caso abbiamo impostato una massa variabile ben definita e abbiamo verificato la conservazione della quantità di moto. Nel secondo, abbiamo imposto la conservazione della quantità di moto (ammettendo che la massa possa variare) e abbiamo trovato la definizione della massa che la verifica. Praticamente la stessa cosa...
Un paio di grafici illustrativi e un piccolo paradosso, proposto anch'esso da Feynamn, che introduce prepotentemente nell'equivalenza di massa ed energia (come vedremo meglio più in là).
Qualche grafico...
La quantità di moto relativistica si può scrivere come (m è la massa a riposo):
qR = mw/(1 - w2/c2)1/2 = m w(c/c)/(1 - w2/c2)1/2 = mc (w/c)/ (1 - w2/c2)1/2
Non è difficile riportare, in Fig. 8, la quantità di moto relativistica (in unità di mc), in funzione del rapporto w/c, confrontandola con quella classica.
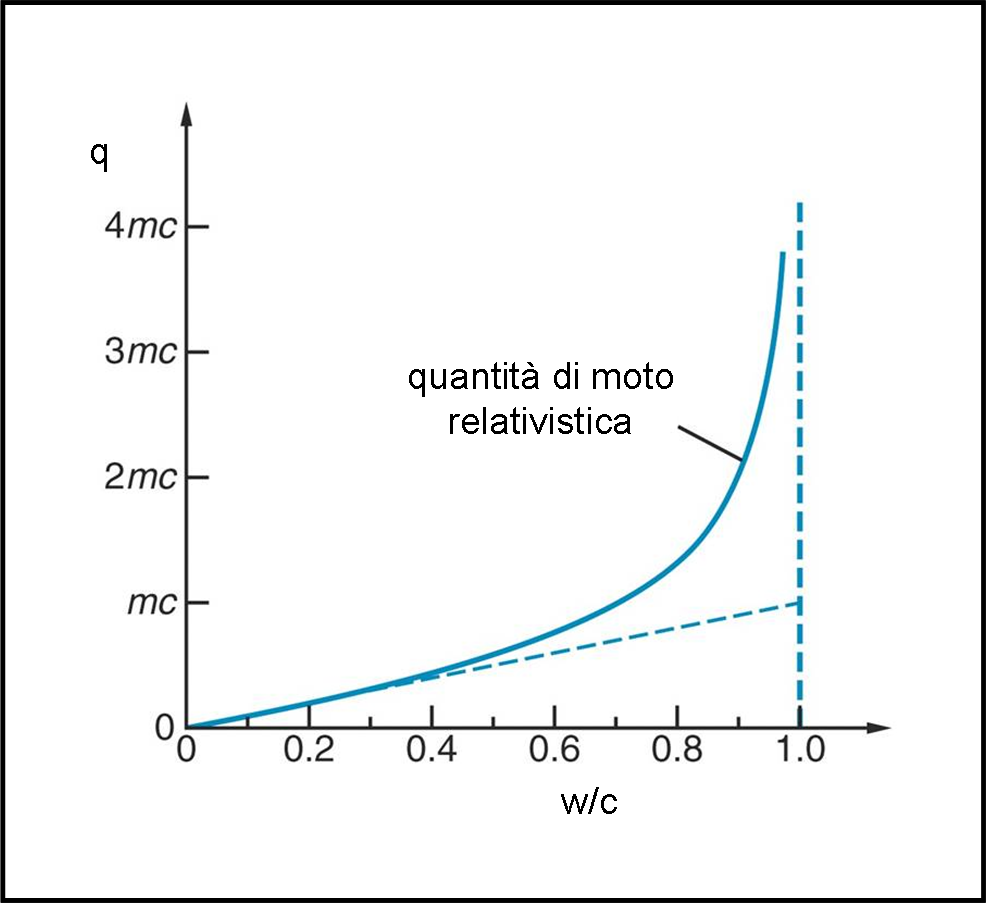
Se preferite, possiamo anche vedere, in Fig. 9, come varia la massa relativistica data da:
mW = m0/(1 - w2/c2)1/2
in funzione dello stesso rapporto w/c e in unità della massa a riposo m0.
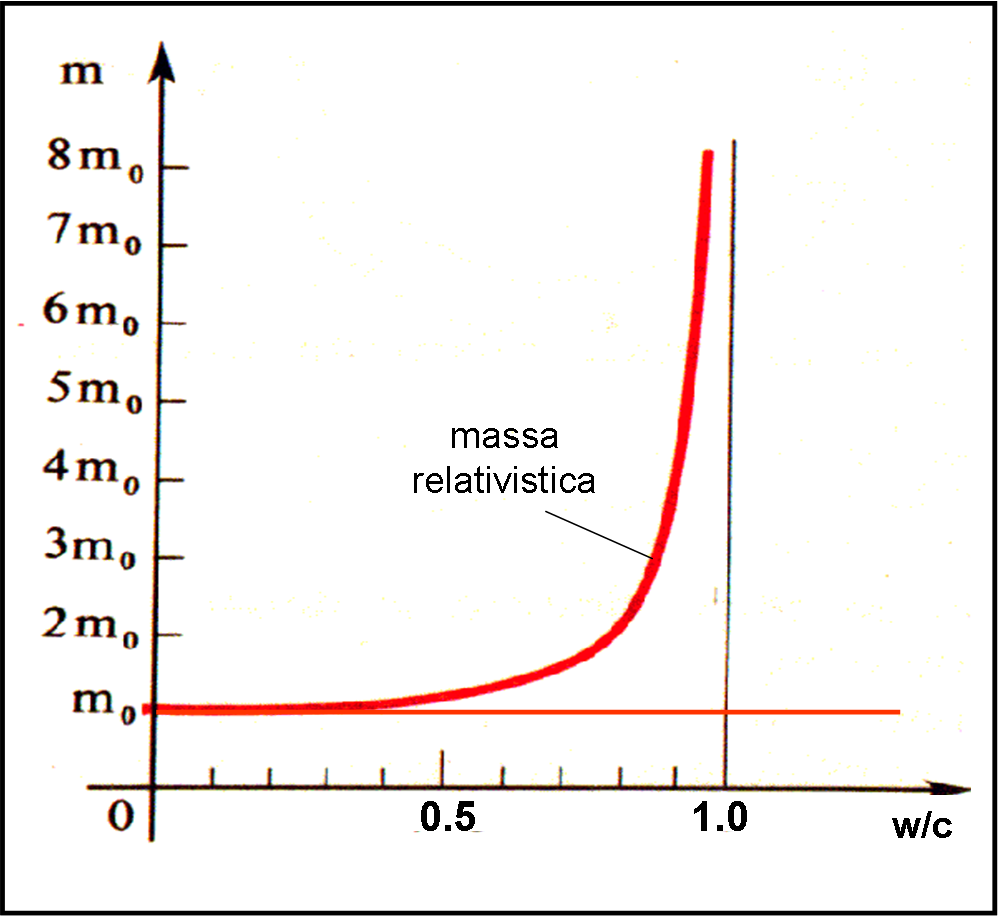
Una sorpresa: la massa non si conserva!
Continuiamo a considerare la massa come una grandezza che cresce con la velocità, pur sapendo i possibili limiti di questa definizione. In realtà, è la quantità di moto che cambia e la variazione viene imputata alla massa. Una massa relativistica diventerà fisicamente “sensata” solo quando si vedrà il suo legame con l’energia. Per adesso, limitiamoci a dimostrare come quanto abbiamo ottenuto finora possa portare a situazioni apparentemente assurde.
Consideriamo un urto perfettamente anelastico tra due palline di uguale massa m che si urtino frontalmente con la stessa velocità di modulo w, ma di segno opposto, come mostrato in Fig. 10 (in alto).
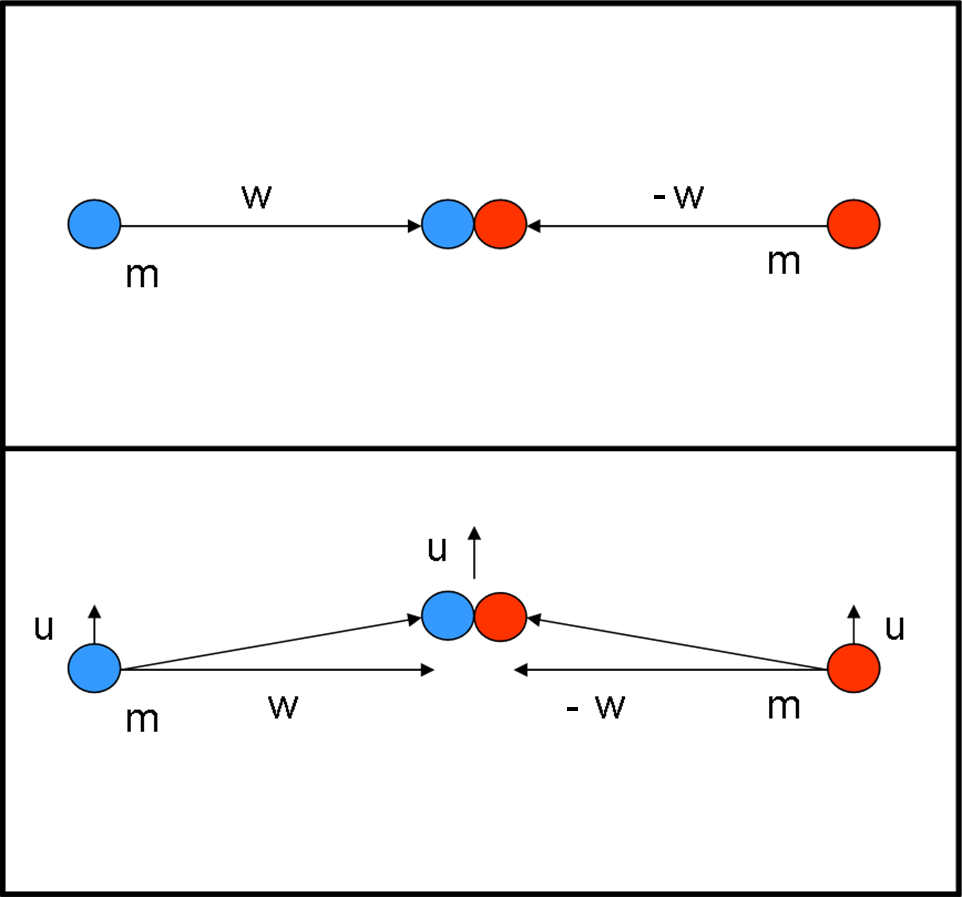
Da quanto abbiamo ricavato le due masse che si muovono a velocità w, devono possedere una massa:
mw = m0/(1 – w2/c2)1/2
Tuttavia, la quantità totale di moto prima dell’urto è uguale a zero e tale deve essere anche dopo l’urto.
Ovviamente:
mww – mww = 0 (prima dell'urto)
M 0 = 0 (dopo l'urto)
Eseguiamo una piccola variazione all’esperimento (Fig. 10, in basso), imprimendo anche una infinitesima velocità u ortogonale a w. Notate che stiamo usando simboli che niente hanno a che fare con la trattazione dei capitoli scorsi. Le due masse si muovono praticamente a velocità w, per cui la loro massa prima dell’urto deve essere praticamente mw. La massa dopo l’urto è una certa massa M, che immaginiamo di non conoscere. La quantità di moto verticale prima dell’urto è dato da:
mWu + mWu = 2mwu
quella orizzontale è:
mww – mww = 0
Quella orizzontale si conserva dopo l’urto anelastico dato che le due masse si uniscono, formando M, e si fermano nella direzione di w (massa M con velocità uguale a zero). Succede la stessa cosa del caso precedente: entrambe le quantità di moto orizzontali sono uguali a zero.
Quella verticale, dopo l'urto, dà luogo a Muu, ossia a un movimento verso l’alto con velocità u della massa M.
Per la conservazione deve essere:
Muu = 2mwu
Tuttavia, u è talmente piccolo che possiamo considerare Mu = M0. Ne segue che:
M0 = 2mw
“Magnifico!”, diciamo, “Abbiamo appena verificato la conservazione della massa. La massa dopo l’urto è esattamente uguale a due volte la massa di ogni singola pallina!”.
Magnifico… proprio per niente!
Per la conservazione della quantità di moto relativistica, la massa M0, che è quella di un oggetto praticamente fermo, deve essere uguale a due volte la massa di due oggetti in rapido movimento (mw). Massa, quest’ ultima, che deve essere decisamente superiore a quelle dell’oggetto fermo (m0). In parole povere, ma non certo -apparentemente- logiche:
M0 > 2m0
Ripetiamo ciò che abbiamo dimostrato: siamo partiti con due masse a riposo (m0). Le abbiamo scagliate a grande velocità una contro l’altra, producendo un urto perfettamente anelastico. Abbiamo, perciò, ottenuto una nuova massa a riposo (M0), che è decisamente maggiore della somma di quelle di partenza!
In altre parole, le masse non si conservano, se vogliamo conservare la quantità di moto relativistica.
In realtà, la conservazione delle masse continua a essere valida, ma solo se vi è un “abbraccio” molto stretto tra massa relativistica ed energia. Ricordiamo, infatti, che in urto anelastico non si conserva l'energia cinetica, ma se mettiamo insieme massa ed energia le cose potrebbero cambiare in meglio! Ma questo è un discorso su cui torneremo molto presto… In pratica: le due leggi di conservazione della fisica classica (di massa ed energia) si uniscono in una sola legge, dato che massa ed energia diventano la stessa cosa...
Dimostrato che nella relatività ristretta è necessario modificare la definizione della quantità di moto, affinché essa si conservi, imponendo che la massa del corpo in oggetto aumenti con la sua velocità, risulta chiaro che le leggi di Newton devono subire anch’esse delle modifiche strutturali, quando le velocità diventano paragonabili a quelle della luce. Cominciamo ad avvicinarci all'energia...
Nessuno vuole distruggere la dinamica classica, ma bisogna accettare che essa valga solo per velocità ridotte, simili a quelle con cui siamo abituati a convivere e che sono, comunque, ancora compatibili con quelle necessarie a trasportare con grande precisione le sonde spaziali in giro per il Sistema Solare. Einstein non distrugge, ma migliora pur rivoluzionando i concetti di base. Sembra ancora impossibile che, scardinando completamente la struttura generale della realtà, sia riuscito a preservare il contributo della fisica precedente. Già questo risultato meriterebbe dieci Nobel…
All'attacco della seconda legge di Newton
Consideriamo subito la legge forse più importante del moto dei corpi, la seconda, quella che dice che una forza è data dalla variazione della quantità di moto rispetto al tempo. Non stupitevi… per Newton è del tutto equivalente alla scrittura più famosa:
F = ma
Infatti:
F = ma = m dv/dt = d(mv)/dt = dq/dt
Attenzione: abbiamo fatto un passaggio che andava bene per Newton, ma non per noi… Abbiamo, infatti, considerato la massa costante inserendola nella derivata.
Noi preferiamo utilizzare, perciò, la relazione:
F = dq/dt
e vedere cosa succede nel caso in cui la quantità di moto sia relativistica. La relazione precedente vale, infatti, nel caso generale, senza imporre niente sulla costanza della massa.
Ammettiamo che un corpo sia soggetto a una forza costante e che sia inizialmente fermo. In poche parole, al tempo t = 0 vale v = 0. Lasciamo che la forza agisca per un certo tempo t. In parole povere, possiamo tranquillamente evitare la scrittura vettoriale e lavorare con i moduli, dato che tutto si muove o fa muovere nella stessa direzione.
Abbiamo una derivata di mezzo e salta subito all’occhio che il modo migliore per far comparire la quantità di moto è quello di integrare entrambi i membri della relazione precedente nell’intervallo di tempo t - 0. In altre parole, sommiamo tutti contributi infinitesimi della variazione della quantità di moto per un certo intervallo di tempo t.
∫0t F dt = ∫0t (dq/dt) dt
Tuttavia, la forza F è una costante e quindi:
∫0t F dt = F ∫0t dt = F (t - 0) = F t
Ricordiamo che l’integrale indefinito di 1·dt non è altro che t
Il secondo membro vede al suo interno proprio una derivata (quella della quantità di moto) e quindi:
∫0t (dq/dt) dt = q(t) – q(0)
Ne segue:
F t = q(t) – q(0)
E, ancora:
F t = q(t) …. (8)
dato che per t = 0 abbiamo v = 0 e, quindi, anche q(0) = 0.
Chi ha un po’ di dimestichezza con la fisica classica, ha già riconosciuto la grandezza che abbiamo appena trovato: il prodotto della forza per il tempo in cui viene applicata. Essa viene chiamato impulso di una forza (un giorno ne parleremo più a lungo, lo prometto). La relazione precedente enuncia una legge della meccanica classica ben conosciuta che dice: l’impulso di una forza è uguale alla variazione della quantità di moto (nel nostro caso, il secondo membro è una variazione dato che q(0) = 0).
Il fatto che l’abbiamo ricavata, senza imporre alcuna costrizione alla quantità di moto, ci assicura che questa legge rimane valida anche nella dinamica relativistica. Sembrerebbe una sottigliezza, ma, invece, è un punto molto importante, dato che la sua validità ci mostrerà tra breve come è costretta a variare la velocità.
Prima di proseguire, volevo tirare un po’ su di morale chi non ha ancora digerito gli integrali.
La relazione:
F = dq/dt
poteva essere scritta:
dt F = dq
o, anche:
∆t F = ∆q
Ossia:
(t – 0) F = q(t) – q(0) = q(t)
Esattamente la (8). Ma allora perché tanta fatica con gli integrali? Beh, nel nostro caso, siamo di fronte a una forza costante e quindi il suo impulso vale anche per intervalli di tempo non infinitesimi. In pratica possiamo sostituire un dt con un ∆t.
La (8) rimane, comunque, un caso particolare di una definizione ben più generale che contempli anche una forza variabile. In tal caso, gli intervalli infinitesimi dt non potrebbero essere sostituiti con intervalli di ampiezza qualsiasi e l’integrale risulterebbe obbligatorio (ricordiamoci che è pur sempre la somma di tante quantità infinitesime).
Stiamo discutendo di dinamica relativistica, lo ammetto, ma le sfumature nella trattazione delle leggi fisiche devono ormai essere tenute in conto. Gli integrali, così come le derivate, devono essere valutati per quello che in realtà significano. Considerare dy/dx = ∆y/∆x può anche essere accettato, in certi casi, ma dobbiamo tenere ben presente il loro diverso significato matematico (e non solo). Una derivata è uguale a un rapporto tra intervalli finiti solo per particolari condizioni.
Per valutare ben la differenza basta andare a rileggere gli articoli che introducevano gli integrali come aree e come somma di tante aree infinitesime. Essi diventano fondamentali quando la funzione non è più una semplice retta, ma varia continuamente la sua pendenza (QUI e QUI)
Va bene, fatti tutti contenti, possiamo tornare alla (8) e chiederci: “Cosa succede alla velocità di un corpo di massa m0 a riposo, su cui agisce una forza costante, se si sostituisce alla definizione di quantità di moto classica quella relativistica?”. Bene, cominciamo col ricordare il primo caso.
- a) Quantità di moto classica
La quantità di moto classica è data da:
q = m0v(t)
La (8) diventa:
F t = m0v(t)
E ancora:
v(t) = (F/m0)t …. (9)
Il rapporto F/m0 è una costante (e sappiamo che prende il nome di accelerazione…), da cui segue che la velocità è una funzione lineare del tempo, ossia descrive una retta che ha proprio l’accelerazione (costante) come coefficiente angolare.
La possiamo disegnare tratteggiata nella Fig. 11, dove alcuni valori "critici" saranno introdotti tra non molto.
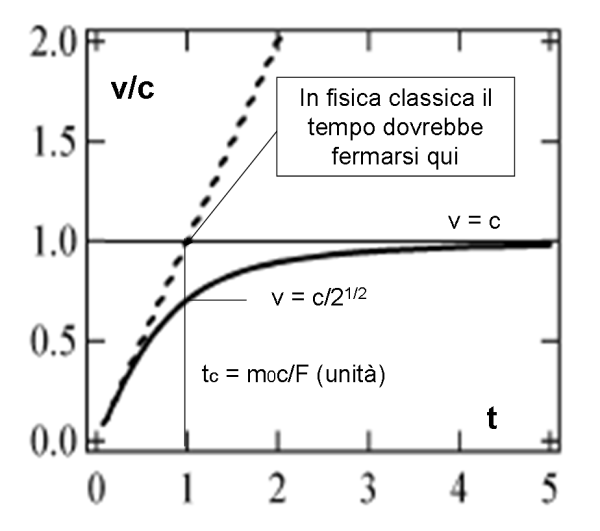
Questo è quanto ci dice la seconda legge di Newton… Purtroppo, il risultato non è accettabile dalla RR. Consideriamo un tempo tc tale che:
tc ≥ m0c/F
Niente può vietarci di raggiungerlo e di superarlo. Avremmo:
v(tc) ≥ (F/m0) (m0c/F) = c
In altre parole, al posto di t possiamo inserire un suo valore qualsiasi, dato che niente blocca il tempo. Consideriamo proprio tc = m0c/F che,sostituito nella (9) porta a un valore di v uguale a c. Per valori di t superiori ne consegue che la velocità supera quella della luce.
E qui le cose non vanno più bene...
Sembrerebbe quasi che la forza possa agire solo per un certo tempo, ma questo non ha alcun senso fisico o almeno non per adesso. In realtà, la forza agisce sempre, ma non comporta un valore costante dell’accelerazione. Il suo sforzo serve sempre di più a far crescere la massa… Lo vediamo subito.
- b) Quantità di moto relativistica
Riprendiamo la (8), ma questa volta utilizziamo la definizione relativistica della quantità di moto, ossia:
qR = mvv(t) = m0 γ v(t)
dove, tanto per non dimenticare:
γ = 1/(1 – v2(t)/c2)1/2
Notiamo, ancora una volta, che la velocità che entra in gioco e proprio la velocità del corpo in movimento.
Sostituendo nella (8), otteniamo:
F t = qR(t) = m0γv(t) = m0v(t)/(1 - v2(t) /c2)1/2
v(t) = F (1 - v2(t) /c2)1/2 t/m0 …. (10)
Notiamo che l’incognita "velocità" si trova sia a sinistra che a destra. E’ necessario risolvere l’equazione (10), in modo da esplicitare la velocità in funzione del tempo. Non è certo impresa difficile… basta un po’ di matematica elementare. Ad esempio, eleviamo al quadrato entrambi i membri:
v2(t) = F2 (1- v2(t) /c2) t2 /m20
m20 v2(t) = F2 t2 - F2 v2(t) t2/c2
v2(t) (m20 + F2t2/c2) = F2 t2
v2(t) = F2 t2/(m20 + F2t2/c2)
v(t) = Ft/(m20 + F2t2/c2)1/2 …. (11)
Questa è una funzione del tempo che sappiamo sicuramente studiare. In particolare, possiamo facilmente calcolare l’asintoto orizzontale che si ottiene facendo tendere il tempo a infinito.
Il limite della v(t) diventa una forma infinito su infinito, ma sappiamo bene come risolverlo, dato che numeratore e denominatore hanno lo stesso grado (la radice quadrata di t2 ha lo stesso grado di t). Il limite si riduce al rapporto tra i due coefficienti dei termini di grado massimo:
lim t→∞ Ft/(m20 + F2t2/c) = c F/F = c
L’asintoto orizzontale è dato dalla retta v = c. In poche parole, la velocità non può superare la velocità della luce. Sì, adesso le cose vanno molto meglio, come si vede dalla curva continua della Fig. 11.
Tuttavia, la (11) merita tutta una serie di riflessioni che troppo spesso non vengono sufficientemente evidenziate.
Una "strana" velocità
Riflettiamo un po’ sulla nuova velocità, su quello che riesce a fare una forza e sulla fantasia scientifica. Un momento in cui tirare il fiato per poi lanciarsi verso la massa-energia , tante volte citata, ma, non sempre, veramente compresa.
Finora non abbiamo parlato di unità dell’asse del tempo nella Fig. 11 che riproponiamo come Fig. 12.
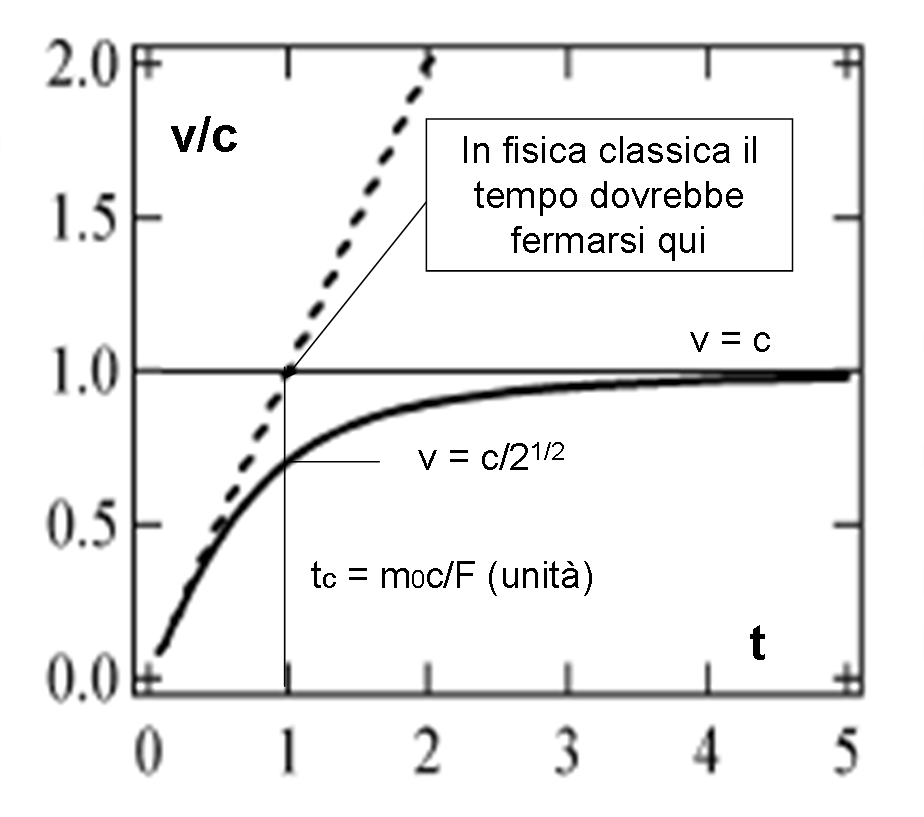
Non ve ne era bisogno, ma tanto vale introdurla. Essa altro non è che quella che corrisponde al tempo:
tU = m0c/F (il tempo “critico” della volta scorsa)
Per questo valore il denominatore della (11) diventa uguale a √2 m0. A ciò corrisponde una velocità pari a:
v(t0) = (Fm0c/Fm0√2) = c/√2
E’ facile notare che per valori molto inferiori a t = 1, la curva tratteggiata (classica) è praticamente coincidente con quella relativistica. La (11) si riduce praticamente alla (9).
In altre parole, data una certa massa, non si può fare agire per troppo tempo una certa forza, se no la fisica classica perde di significato e la velocità assume un andamento assurdo. Invece, ciò è del tutto possibile con la nuova definizione di velocità. In realtà, la forza continua ad agire, ma il suo contributo non si riversa tutto sulla velocità. Se non si riversa sulla velocità vuol dire che cambia il modo di farla variare, ossia l’accelerazione (quella che comanda la variazione della velocità) comincia a perdere “colpi”.
Notiamo, infatti, che la pendenza istantanea della curva velocità (ossia l’accelerazione) non rimane assolutamente costante, anche se la forza lo è. E questo è un qualcosa che farebbe sobbalzare il povero Newton. In particolare, l’accelerazione decresce all’aumentare della velocità. Ciò deriva dal fatto che mentre la velocità aumenta, aumenta anche la massa della particella (m0γ). Teoricamente per velocità prossima a quella della luce, l’accelerazione tende a zero.
Potremmo, ad occhio per adesso, determinare tre zone nella curva: (a) quella iniziale rettilinea in cui l’applicazione della forza causa un aumento lineare dell’accelerazione. La massa praticamente non cambia. (b) La seconda che può essere chiamata relativistica, in cui la forza fa aumentare sia la velocità, ma in modo meno rapido, che la massa del corpo, in grado, perciò, di controbattere sempre più all’accelerazione: l’inerzia aumenta. Ovviamente, per cercare di raggiungere una certa velocità è necessario fare agire la forza per tempi molto lunghi. (c) La terza zona (ultra relativistica) torna a essere quasi rettilinea, ma in direzione… orizzontale. Quasi tutta l’azione della forza si traduce in un aumento della massa e la velocità resta praticamente costante, essendo ormai prossima a quella della luce.
Possiamo dire tranquillamente che la velocità di qualunque corpo materiale che abbia una massa inerziale a riposo diversa da zero non può mai raggiungere valori uguali o superiori a c.
Infatti, a mano a mano che aumenta la velocità del corpo, a causa dell'aumento della massa, l'accelerazione diminuisce e la velocità cresce più lentamente avvicinandosi sempre più al valore limite v = c, che viene raggiunto solo nel limite di un tempo infinito.
Quanta fisica rivoluzionaria c’è dentro a queste semplici riflessioni… Abbiamo una massa inerziale che aumenta e che costringe, a parità di forza, a diminuire l’accelerazione e di conseguenza a far crescere la velocità sempre più lentamente.
All’interno di questa frase è già presente il concetto che evidenzia l’impossibilità di raggiungere velocità troppo alte con oggetti di massa “normale”, dato che bisognerebbe fornire un’energia incredibilmente alta. Cosa, questa, che vedremo meglio in seguito… In ogni modo, già capiamo che, per raggiungere una velocità uguale a quella della luce, la massa dovrebbe diventare infinita (quanta fatica dovrebbe fare la forza…).
Ma, in realtà, esiste qualcosa che va alla velocità della luce… anzi che può esistere solo muovendosi a quella velocità. Lo conosciamo molto bene: il fotone. Ma allora il fotone ha sempre massa infinita? No, nemmeno lui può arrivare a tanto e ce lo dice un concetto matematico molto semplice. E’ vero che il denominatore della sua massa relativistica tende a zero, ma fa lo stesso anche il suo numeratore, dato che la massa a riposo è uguale a zero. E zero su zero è una forma indeterminata. Non per niente, il fotone ha un’energia finita e tra poco vedremo che massa ed energia sono praticamente la stessa cosa…
Per riuscire, comunque, a portare la velocità a livelli molto alti è necessario avere a che fare con particelle molto piccole. Per loro è decisamente più facile raggiungere accelerazioni elevatissime attraverso speciali strumentazioni, che ben conosciamo: gli acceleratori di particelle.
Possiamo senz’altro concludere che il mondo della relatività speciale è proprio quello degli elettroni, dei protoni e dei loro fratellini.
Vale, però anche il contrario… Poter imprimere accelerazioni così grandi a particelle elusive, ma concrete, permette di verificare la perfetta validità della (11) anche per velocità prossime a quella della luce. La teoria ha dovuto aspettare proprio loro per mostrare la sua immensa portata.
Particelle insignificanti per l’Universo? O addirittura del tutto ipotetiche e mai rilevate? Assolutamente no. Anzi, proprio i mattoni fondamentali di tutto ciò che esiste. Vi sembra poco?
Qualche riflessione...
La teoria della RR è una vera teoria scientifica che ha fornito tutte le possibilità alla mente e alla tecnologia umana per potere essere confermata osservativamente. Tanto di cappello, signor Einstein!
No, cari amici, la dinamica relativistica non è difficile, ma senza averne una conoscenza sufficiente (anche se non specialistica) è ASSURDO disquisire su relatività generale, curvatura dello spaziotempo, densità critica dell’Universo, buchi neri, radiazione di Hawking, energia negativa, wormhole, singolarità, onde gravitazionali e mille altri argomenti ai confini della Scienza attuale.
Ricordiamoci (e un giorno -forse- riusciremo a parlarne diffusamente) che proprio dalla formula più importante della RR (non quella più mediatica) è nato il mare di Dirac e il concetto di energia negativa. La fantasia può anche essere libera di volare, ma se mancano le basi “fondamentali”, diventa pura fantascienza, poco divertente e ancora meno utile, sia per chi la scatena sia per chi la subisce. Tutti voi sapete benissimo a chi e a cosa mi riferisco…
Dirac poteva anche permettersi di immaginare un’energia negativa, così come Planck poteva anche pensare all’energia regalata a “pacchetti” (e non ne era nemmeno troppo convinto). Entrambi conoscevano bene ciò che era stato raggiunto dalla Scienza fino a quel punto. La loro fantasia poteva e doveva volare. Ma chi non conosce nemmeno le leggi di Newton, o giù di lì, può permettersi di prospettare teorie alternative a quelle su cui veri scienziati hanno trascorso anni e anni di dura riflessione e di studio? No, non lo posso accettare e quel novello “genio” dovrebbe essere zittito immediatamente. Vi sono mille modi per sfogare la propria fantasia e quel felice e puro mondo di Papalla ce lo insegna.
Scusate questi sfoghi, ma li reputo importantissimi soprattutto per i giovani. Quando ho letto (poco tempo fa) che un maturando vorrebbe scrivere una tesina sul ponte di Einstein-Rosen e sulle formule applicate ai wormhole, mi sono venuti i brividi. La ragione ultima è solo mediatica, ossia la visione di un recente film di fantascienza (sbaglia perfino il nome del ponte, inserendo quello del fantomatico pianeta del film), ma la richiesta apre un baratro terribile sull’insegnamento scolastico e sulla facilità di trovare di tutto e di più sulla rete, senza nessun segnale di pericolo.
Ci si accorge subito che, ovviamente, quel ragazzo non ha la più pallida idea della RR e della RG, tranne poche frasi fatte e vaghi concetti confusi. E’ il momento di bloccarlo, di fargli capire che certi argomenti non si inventano dall’oggi al domani, che hanno dietro costruzioni logiche, fisiche e matematiche enormi. Comprensibili sì, ma con tanta dedizione e attenzione. Soprattutto, bisognerebbe dirgli che anche nel mondo virtuale e del “copia e incolla” di oggi è necessario studiare!
E, invece, lo si incoraggia anche, facendogli capire, tra le righe, che chiunque potrebbe, in fondo, disquisire di certe faccende scientifiche. No, non voglio considerare la Scienza come “cosa” da "elite" dei cervelli. Proprio il contrario. Vorrei solo far capire che i castelli hanno bisogno di fondamenta se no crollano al primo alito di vento. E, poi, se non altro, per un minimo di rispetto verso i grandi filosofi greci, Galileo, Giordano Bruno, Newton, i fisici dell’ottocento e del primo novecento, e -non certo ultimo- il nostro Einstein.
Concludo subito questo intermezzo, che ho inserito volontariamente all’interno della dinamica relativistica. Solo chi ha sentito il bisogno di entrare senza timore o falsa arroganza nella realtà einsteniana è in grado di capire appieno le motivazioni di questi sfoghi e di aiutarmi a riportare i giovani sulla giusta strada della conoscenza. Stiamo lontani e - nel caso- osteggiamo con forza chi disquisisce, senza alcuna base solida, di fantasie scientifiche personali e si convince (ed è anche incoraggiato a farlo) di fare Scienza!
Forza costante, accelerazione che perde i colpi, velocità timorosa di giungere a livelli troppo alti, inerzia al moto che cresce con la velocità, energia che si affaccia in modo innovativo… e tutto ciò solo imponendo la costanza della velocità della luce o poco di più. Questa è fantasia geniale!
Va bene, è giunta l’ora di affrontare il punto più famoso della relatività. Un punto famoso che diventa quasi ovvio proseguendo con logica e conoscenza. La vera grandezza di Einstein è che LUI lo aveva già previsto perfettamente, ben prima di arrivarci con le formule.
Energia cinetica relativistica
Dimostrato che nella relatività ristretta è necessario modificare la definizione della quantità di moto, affinché essa si conservi, imponendo che la massa del corpo in oggetto aumenti con la velocità, risulta chiaro che le leggi di Newton devono subire delle modifiche strutturali, quando le velocità diventano paragonabili a quelle della luce.
Un po’ ovunque si può trovare la definizione di energia cinetica come lavoro fatto da una forza per portare un corpo da una certa posizione iniziale, in cui è fermo (velocità zero), a una finale con velocità v. Il tutto viene effettuato a partire dal tempo zero per arrivare al tempo t. In poche parole, tempo zero, posizione zero e velocità zero individuano l’inizio del lavoro, mentre s, t e v indicano la fine.
Consideriamo il caso più semplice, in cui lo spostamento del corpo avvenga sempre lungo la stessa direzione. Non dimentichiamo mai che il lavoro è una differenza di energie e viene definito come il prodotto scalare (QUI) tra la forza e lo spostamento (due vettori). Dato che stiamo lavorando in una sola direzione, possiamo tranquillamente passare ai moduli e scrivere:
L = F ∆s
Sappiamo già il risultato, ricordando che l'energia cinetica di un corpo fermo è uguale a zero, …
L = F ∆s = KF – KI = ½ mv2(t) – ½ mv2(0) = ½ mv2(t) = K
Partiamo dalla definizione di lavoro e arriviamo alla classica definizione dell’energia cinetica acquisita dopo un certo tempo t, dopo aver percorso lo spazio s e aver raggiunto la velocità v.
Non vogliamo ripetere il calcolo che si può trovare ovunque e che si riferisce alle basi della meccanica classica (basta ricordare il moto uniformemente accelerato). Noi vogliamo utilizzare il calcolo integrale (vedi le lezioni relative agli integrali nell'approfondimento sulla Matematica, dal numero 51 al 61) . D’altra parte dobbiamo proprio sommare tanti prodotti infinitesimi F ds da s = 0 a s = s.
Scriviamo, quindi, senza esitazione (ricordando che v = ds/dt):
L = ∫0s F ds = ∫0s (dq/dt) ds = ∫0s (d(mv)/dt)ds = ∫0t (d(mv)/dt)vdt = ∫0v (v d(mv)
Notate che abbiamo cambiato i limiti di integrazione a seconda della variabile considerata, sapendo bene che a t = 0 corrispondono s = 0 e v = 0 e a t = t corrispondono s = s e v = v (queste erano le ipotesi di partenza e di arrivo)
Nel caso classico, m = m0 = cost.
L = ∫0t F ds = ∫0v m0v dv = ½ m0v2 – ½ m0 0 = ½ m0v2 = K
L’energia cinetica K è proprio data da:
K = ½ m0v2
Abbiamo eseguito un integrale immediato (QUI), del tipo:
∫ x dx = x2/2 + c
Non ci resta, adesso, che introdurre la nuova definizione di quantità di moto e vedere come si trasforma l’energia cinetica di un corpo che parte da fermo e arriva alla velocità v.
∫0s F ds = ∫0s (dq/dt) ds = ∫0s (d(m0γv)/dt) ds = ∫0t (d(m0γv)/dt) v dt …. (12)
Dobbiamo perciò calcolare l’integrale nel tempo della funzione:
P(t) = F v = v d(m0γv)/dt …. (13)
Non l’abbiamo chiamata P(t) a casaccio. Essa è proprio la potenza meccanica, ossia il lavoro compiuto nell’unità di tempo. Infatti:
P = dL/dt = F ds/dt = F v
Tuttavia, è inutile entrare nei dettagli, dato che il nostro scopo è ben altro.
La (13) non ci piace tanto come funzione di cui calcolare l’integrale. C’è una bella derivata già pronta, ma c’è anche una v sola soletta. Niente paura! Andiamo a recuperare un quiz che avevamo proposto poco tempo fa (QUI) con la relativa soluzione (QUI). Riportiamo comunque quanto è stato chiesto in quel quiz e la sua soluzione, per meglio legarlo alla nostra trattazione.
Vogliamo dimostrare che:
v·d(γ·v)/dt = c2· dγ/dt .... (14)
dove v è la velocità, funzione del tempo, c la velocità della luce (costante) e γ = 1/(1 – (v/c)2)1/2 (ben noto a tutti i relativistici…).
La prima cosa da fare è riproporre l’uguaglianza da verificare, scrivendo per esteso la derivata del primo membro:
v2dγ/dt + γv dv/dt = c2 dγ/dt …. (15)
Partiamo direttamente dalla definizione di γ:
γ = 1/(1 – (v/c)2)1/2
Qualche piccolo ritocco, dopo aver elevato a quadrato
γ2 - γ2v2/c2 = 1
γ2c2 - γ2v2 = c2
Deriviamo questa espressione rispetto al tempo (sia γ che v sono funzioni del tempo), ricordando la derivata del prodotto e la costanza di c:
2c2γdγ/dt - 2γv2dγ/dt - 2γ2v dv/dt = 0
Semplificando i termini comuni si ottiene:
c2dγ/dt - v2dγ/dt - γv dv/dt = 0
spostando qualcosa a destra del segno di uguale si ha, infine:
v2 dγ/dt + γv dv/dt = c2dγ/dt …. (16)
Che è esattamente uguale alla (14), che è quindi verificata!
Riassumendo, è stato dimostrato che:
v·d(γ·v)/dt = c2· dγ/dt
Moltiplichiamo entrambi i suoi membri per m0 (costante) e otteniamo:
m0v·d(γ·v)/dt = c2· m0·dγ/dt
Magnifico! Possiamo allora inserire questa funzione all’interno dell’integrale (12)
∫0t m0 (d(γv)/dt) v dt = ∫0t c2· m0 (dγ/dt) dt = c2· m0 ∫0t (dγ/dt) dt
Quasi per miracolo, ci troviamo di fronte all’integrale di una derivata e quindi la sua soluzione è immediata (l’integrale è quella funzione la cui derivata è proprio la funzione da integrare):
K = ∫0s F ds = c2· m0 ∫0t (dγ/dt) dt = c2· m0 (γ(t) – γ(0)) = c2· m0 (γ(t) -1)
Ricordiamo, infatti, che (per t = 0, abbiamo v = 0)
γ(0) = 1/(1 – v2/c2) = 1/(1 – 0) = 1
Ancora un passaggio e …
K = c2· m0 γ - c2· m0 = m c2 – m0 c2 …. (17)
Dove m è la massa relativistica.
Ribadiamo subito un fatto fondamentale che abbiamo già toccato precedentemente. La massa relativistica m tende ad infinito per v che tende a c. Ne consegue che l'energia cinetica di un corpo di massa diversa da zero tende a infinito.
In altre parole: per fare acquistare una velocità pari a c a un corpo di massa a riposo non nulla, sarebbe necessario fornirgli un'energia infinita (ricordiamo che per ottenere energia cinetica è necessario far compiere lavoro a una forza). Questo è il motivo FISICO per cui la velocità della luce rappresenta una velocità limite per qualunque corpo materiale.
Ci torneremo ancora sopra (e come), ma possiamo dire che l’energia cinetica relativistica non è altro che la differenza di due energie (le unità di misura tornano perfettamente). Non fatevi ingannare dal fatto che non vedete la velocità espressa apertamente: essa è compresa nella massa relativistica m.
La formula più famosa del mondo
Assumendo come energia totale E di un corpo in movimento la quantità mc2 (deve essere un’energia da come è stata trovata!) si ha:
E = m c2 = m0 c2 + K
L’energia totale di un corpo è data dalla somma di due termini. Il primo è l’energia del corpo quando è in quiete, il secondo è la sua energia cinetica. In altre parole, anche se il corpo resta fermo (K = 0), esso possiede comunque un’energia che dipende soltanto dalla sua massa a riposo (moltiplicata per una costante). Non confondiamola con l'energia potenziale gravitazionale, mi raccomando! Non abbiamo nessun campo gravitazionale...
Ripetiamo ancora un risultato fondamentale per tutta la fisica: Un corpo in quiete possiede una certa energia a riposo (E0) e questa è data proprio dalla sua massa a riposo (a meno di una costante moltiplicativa):
E0 = m0c2
La vera legge relativistica rimane, comunque:
E = mc2
In cui la massa è funzione della velocità (ricordiamolo sempre!)
Massa ed energia sono la stessa cosa! Questa conclusione è ancora più evidente se decidiamo di misurare il tempo in metri-luce (ricordate?). In questo caso, come abbiamo visto nella RR, la velocità della luce diventa un parametro senza dimensioni ed è uguale all’unità. Ossia:
E = m
Guardiamola bene e ammiriamola in silenzio: questa semplice formula è un risultato mostruosamente importante per tutta la fisica moderna. E l’abbiamo ricavata con ben poca difficoltà (esistono anche altri metodi, alcuni dei quali apparentemente più semplici, ma troppo legati alla matematica e si perde il senso fisico che abbiamo mantenuto passo dopo passo).
Se ne potrebbe discutere per ore e si scoprirebbero infinite conseguenze fondamentali per tutti i campi della Scienza (chimica, termodinamica, fisica nucleare, …), senza escludere -purtroppo- nemmeno quello militare. Qualcuno la studieremo in dettaglio, ma ormai siamo in grado di capire tutto ciò che leggeremo a riguardo. Le basi sono state fissate e quello che serve è solo passione e applicazione.
Cari amici, ci siamo finalmente arrivati. E’ sempre una bella soddisfazione non prendere la formula come una specie di etichetta misteriosa, ma vederla comparire attraverso la logica.
Notiamo subito una cosa poco scientifica, ma molto indicativa: la sua semplicità! Si può dedurre con metodi più o meno facili (almeno per il nostro cervello), ma quando appare, sembra addirittura misera e ovvia. Tutto lì? Ebbene sì. Non c’è scritto da nessuna parte che la Natura debba usare formule complicate per costruire le sue leggi. Anzi, più le formule diventano semplici e più si può essere sicuri di essere vicini alla verità.
Va poi aggiunta una considerazione spesso trascurata, che abbiamo già ”toccato”.Einstein non l’ha dedotta casualmente alla fine di tanti calcoli laboriosi. Lui ne ha subito avuto l’intuizione e tutte le formule sono praticamente servite a confermarla e a legarla alle altre leggi fisiche, senza realmente distruggerne nessuna. Uno dei punti cardini della sua teoria è conservare i risultati di Newton per velocità “normali”. Quanti scienziati odierni avrebbero agito in questo modo? Basta vedere le idee rivoluzionarie che, pur basandosi sul niente, cercano prima di tutto di far crollare i pilastri portanti… poi si vedrà.
Non so se Einstein sia stato una persona con turbe emotive e nemmeno mi interessa la sua vita privata. So soltanto che Galileo, e lo stesso Newton, gli avrebbero stretto la mano!
Questa formula è sicuramente la più famosa, anche se porterà a qualcosa di ancora più eccezionale. E’ mai possibile? Sì, dato che attraverso una semplice uguaglianza ricaveremo nientemeno che un nuovo invariante relativistico, qualcosa che non cambia cambiando il sistema inerziale (vi ricordate la “distanza” spaziotemporale s2? In caso negativo, andate a rileggere questo articolo). Quello che sembra già un capolavoro può perfino essere superato!
Torniamo con i piedi per terra e lasciamo da parte (si fa per dire) l’emozione.
Questo fantastico abbraccio tra massa ed energia fa sì che, quando si tratti con particelle estremamente piccole, si preferisca (e sia più conveniente) esprimere la massa in termini di energia. In particolare si usa l’elettronvolt (eV) o, più comunemente, il suo multiplo (106) megaelettronvolt (MeV). L’elettronvolt rappresenta l’energia acquistata da un elettrone che viene accelerato da una differenza di potenziale di un volt. Tanto per fare un esempio, ricordiamo che la massa a riposo dell’elettrone è uguale a 0.511 Mev.
Dov'è il legame con Newton?
Qualcuno potrebbe commentare: “Abbiamo scritto la nuova versione dell’energia cinetica e il risultato ci ha emozionato e ci ha fatto perdere di vista la realtà… La formula ricavata non ha alcuna somiglianza con quella classica. Eppure, per basse velocità dovrebbe coincidere con lei…”. Questo qualcuno avrebbe ragione. Per noi è un vero piacere dimostrargli che in effetti è proprio così. Un piacere, anche perché sfrutteremo di nuovo gli sviluppi in serie! Anzi, proprio uno che avevamo risolto come esercizio (QUI).
Consideriamo la funzione:
(1 + x)α …. (18)
Il suo sviluppo in serie risulta:
(1 + x)α = 1 + αx + (α – 1)x2/2! + …
E non c’è nemmeno bisogno di andare oltre. Anzi, possiamo già fermarci ai primi due termini. Se x << 1, basta e avanza…
Non ci credete? Basta provare…
Scegliamo
α = ½
e
x = 0.01
Facendo i conti:
(1 + 0.01)½ = 1.00498
1 + 0.01/2 = 1.00500
La differenza è di un 2 sulla quinta decimale.
Prendiamo, adesso:
x = 0.0001
(1 + 0.0001)½ = 1.000049999
1 + 0.0001/2 = 1.000050000
La differenza è diventata solo un 1 sulla nona cifra decimale.
Immaginiamo, per un momento (ma non solo…), che la nostra x sia uguale a (v/c)2
x = 0.0001
vorrebbe dire
x = v2/c2 = 0.0001
ossia (circa):
v = 3000 km/sec
Una velocità niente male… possiamo accontentarci! Sicuramente Newton lavorava con velocità più basse.
Riprendiamo la nostra funzione e poniamo allora:
x = - (v/c)2
e
α = - 1/2
Essa diventa
((1 - (v/c)2))-1/2 = 1/(1- (v/c)2)1/2
Questa funzione la conosciamo molto bene! Non è altro che il fattore γ !
Ma, allora, possiamo sviluppare in serie il fattore γ fermandoci al secondo termine:
γ = 1 + (v/c)2/2
e poi inserirlo nella formula dell’energia cinetica relativistica:
K = c2· m0 γ - c2· m0
Si ha:
K = m0c2 (1 + v2/c2)/2 – m0c2 = ½ m0v2
Che è proprio l’energia cinetica newtoniana!
Eh sì, Einstein ha sempre ragione!
Ricaviamo la celebre formula partendo dalla massa relativistica
Il procedimento usato per verificare la legge newtoniana, ci stuzzica a ribaltare la situazione. Un qualcosa che, in fondo, è molto più vicina al procedimento mentale di Einstein. Vale la pena proporla.
Cosa abbiamo fatto finora? Siamo partiti dall’energia cinetica e, applicandole la “nuova” quantità di moto, siamo arrivati fino a quella relativistica, senza troppa difficoltà. Abbiamo toccato gli integrali, ma ben poca cosa. Insomma, è stato più facile del previsto. Tuttavia, abbiamo anche visto che trafficando con le serie e con il fattore gamma siamo riusciti a ottenere la vecchia formula newtoniana.
Non è, perciò, assurdo pensare che potremmo ottenere la celebre formula partendo solo dalla massa relativistica.
Consideriamo la formula che ci descrive la massa relativistica (ormai dovremmo conoscerla a memoria):
m = m0 γ = m0/(1 – v2/c2)1/2
La trattazione attraverso la serie utilizzata prima ci porta facilmente a:
m = m0γ = m0(1 + (v/c)2/2) = m0 + m0(v/c)2/2
Come può essere interpretata questa formula?
Presto detto: la massa relativistica è uguale alla massa a riposo più una quantità che cresce con la velocità v. Niente di speciale, ma estremamente importante per una mente fuori dal comune.
Scriviamola un po’ meglio:
m = m0 + ½ m0 v2 (1/c2) …. (19)
questo vuol dire che la differenza di massa è uguale all’ energia cinetica divisa per c2. Un modo molto semplice e fisico per descrivere la variazione di massa. Tuttavia, se moltiplichiamo tutto per c2, al secondo membro otteniamo proprio l’energia cinetica:
mc2 = m0c2 + ½ m0 v2
Stiamo, allora, parlando proprio di energia e il primo termine può essere interpretato come l’energia totale di un corpo in movimento e il secondo, dopo l’uguale, un’energia che il corpo possiede anche da fermo. La differenza tra queste due energie è proprio l’energia dovuta soltanto al movimento. Questa trattazione è possibile solo mettendosi nel caso di velocità molto basse, tali da poter esprimere il fattore γ come sviluppo in serie e troncandolo rapidamente. Una visione, in qualche modo “parziale”, ma sufficiente a far comprendere il risultato più generale.
Einstein ha espresso il semplice ragionamento ipotizzando un esperimento reale, estremamente fisico e non matematico.
Lui ha considerato una certa massa di gas contenuta in un recipiente. Immaginiamo di riscaldarlo. Ne segue che le molecole del gas cominciano a muoversi più velocemente e, di conseguenza, la massa del gas deve crescere. La (19) ci dice che l’aumento della massa dovuta al movimento delle molecole è data proprio da m0(v/c)2/2 (abbiamo fatto una semplice differenza). Quando la temperatura aumenta, la velocità delle molecole aumenta in modo proporzionale, per cui si può dire che l’aumento della massa è dovuta all’aumento della temperatura. Tuttavia, ricordando la formula newtoniana dell’energia cinetica possiamo concludere che l’aumento della massa non è altro che l’aumento dell’energia cinetica divisa per c2. In poche parole
∆m = ∆K/c2
La differenza di massa è un’energia divisa per c2. Da cui l’intuizione vincente che la massa non è altro che un’energia divisa per c2. E’ quindi sufficiente moltiplicare la (19) per c2 per ottenere l’energia totale e come essa si suddivide:
E = mc2 = m0c2 + K …. (20)
L’ energia totale è uguale all’energia a riposo più l’energia cinetica.
Sembra di girare in tondo, ma Einstein aveva solo bisogno di applicare a un fenomeno naturale la sua idea di fondo. In questo modo tutto tornava perfettamente anche dal punto di vista fisico..
Come abbiamo visto, Einstein sapeva già cosa voleva e non si era certo meravigliato di trovare la sua formula partendo da lontano… In qualche modo mi ricorda ciò che aveva fatto il grande Giuseppe Colombo, meccanico celeste padovano di levatura immensa. Mentre la NASA preparava le prime missioni su Mercurio, lui aveva avuto l'ispirazione. Un'ispirazione puramente fisica: una navicella può sfruttare la gravità di un pianeta per acquistare velocità e risparmiare carburante. In poche parole, aveva ideato l'effetto fionda . Ebbene, era talmente sicuro della sua intuizione che aveva chiesto ai collaboratori di fare i calcoli, dato che per lui il risultato era già evidente e confermato. Ovviamente, la NASA bloccò subito la missione, in attesa che Colombo le fornisse la nuova traiettoria. Intanto, in Italia, avevano cancellato la sua cattedra di Meccanica Celeste a Padova per scarso interesse applicativo...
Va bene torniamo a noi...
In ogni modo, non facciamoci ingannare dalla semplicità della formula:
E = mc2
Essa deve essere spiegata e capita molto bene. La relazione vale se la massa m è quella relativistica. Se volessimo usare la massa a riposo (quella con cui abbiamo normalmente a che fare) dovremmo trasformare la celebre formula di Einstein in:
E = m0c2/(1 – v2/c2)1/2 …. (21)
Se volessimo, invece, descrivere l’energia a riposo E0, ossia l’energia posseduta da un corpo per il solo fatto di avere una massa, allora dovremmo scrivere:
E0 = m0c2
Sembrano finezze e cavilli inutili… ma spesso l’uso un po’ troppo spavaldo della formula porta a confusioni e fraintendimenti anche gravi.
Ragioniamo sopra alla (21).
Con questa definizione di energia, Einstein unifica i due concetti di massa ed energia, che avevano costituito due capisaldi separati nella storia della Scienza a causa delle due leggi di conservazione ad essi collegati. L’unificazione delle due leggi presuppone la conservazione simultanea di massa ed energia e non di ciascuna di esse considerate singolarmente.
Ciò significa che si debbano avere sia processi di produzione di energia con scomparsa di una frazione di massa del sistema, sia processi di generazione di materia con scomparsa di energia. Come sempre, per il grande Albert, le conferme arriveranno nel tempo, sia attraverso le reazioni nucleari sia attraverso la creazione di particelle e antiparticelle. Tutta la teoria della relatività era troppo avanti per la tecnologia dei tempi in cui è stata descritta. Di conseguenza, nessun Nobel… Questa è la punizione con chi si diverte con velocità simili a quelle della luce…
Fermiamoci un attimo a riflettere per ricollegarci alla RR che abbiamo studiato fin dall’inizio. La celebre formula ci dice che l’energia dipende dal sistema di riferimento. Se sono solidale con il corpo in moto la sua energia è solo quella di riposo. Se sono in un sistema diverso, l’energia si separa in due termini e più la velocità aumenta e più l’energia osservata è praticamente solo quella cinetica.
Riassumendo: l’ energia totale di un corpo è diversa in sistemi di riferimento diversi. Essa dipende dalla velocità del corpo rispetto al sistema di riferimento e il valore minimo di energia si ha nel sistema di riferimento in cui il corpo è a riposo. Tale valore è detto energia di riposo e vale:
E0 = m0 c2
L’energia a riposo, a causa del valore estremamente elevato della velocità della luce, corrisponde a valori molto grandi anche nel caso di masse molto piccole.
In questo contesto, è molto utile tornare sul concetto già espresso che dice: l’energia cinetica di un corpo è la differenza tra la sua energia totale e la sua energia di riposo, cioè l’energia cinetica è un surplus di energia che il corpo acquista quando viene osservato in movimento. In pratica la ormai ben nota formula (20):
K = mc2 – m0c2
Ne segue che per stabilire se ci troviamo in ambito classico o relativistico, il confronto tra energia cinetica ed energia a riposo del corpo diventa fondamentale (e non c’è più bisogno di guardare soltanto la curva della velocità).
Per velocità molto minori della velocità della luce, l’energia cinetica di un corpo è molto minore della energia a riposo. In effetti:
K/E0 = (m – m0)c2/m0c2 = (m – m0)/m0
K/E0 = m/m0 – 1 = 1/(1 – v2/c2)1/2 – 1
Ma ormai sappiamo molto bene che l’espressione γ = 1/(1 – v2/c2)1/2 può essere espressa con la solita serie se v2/c2 << 1, ossia:
K/E0 ~ 1 + (v/c)2/2 – 1 = (v/c)2/2 << 1
Sembra il solito gatto che si morde la coda, ma in effetti, giocando sempre con le stesse quantità, si dimostra che l’energia cinetica è decisamente minore dell’energia a riposo.
Per contro, alle velocità ultra relativistiche che differiscono di poco dalla velocità della luce, quasi tutta l’energia del corpo è energia cinetica e l’energia a riposo è molto minore di quella cinetica.
In questo caso non si può eseguire lo sviluppo in serie e dobbiamo limitarci a scrivere:
K/E0 = 1/(1 – v2/c2)1/2 – 1
Senza ulteriori approssimazioni.
E’ una sciocchezza, ma potete facilmente ricavarvi una tabella per vedere come varia l’energia cinetica al variare della velocità (anche un grafico, ma la curva è decisamente “schiacciata”). Le due energie diventano praticamente uguali intorno a v = 0.9 c, mentre per v = 0.9999 c si è già a livelli 70 volte maggiori.
Questo tipo di approccio è decisamente più fisico che non quello legato solo alla massa relativistica. L’energia cinetica è qualcosa di realmente “materiale” . Ad esempio, negli acceleratori di particelle si arriva anche a far correre un protone al 99.999999% della velocità della luce, il che comporta un’energia cinetica ben 7500 volte superiore a quella di riposo.
Ricordiamoci sempre, comunque, che la RR regna sovrana: che io vada a una velocità altissima poco conta per me, dato che la mia energia cinetica è uguale a zero nel mio sistema di riferimento. Io posseggo solo un energia di riposo. Nello stesso modo in cui il mio tempo è quello proprio e le distanze sono quelle misurate con il celebre righello unitario. Tuttavia, se vado a sbattere contro un muro, gli effetti sono catastrofici. La spiegazione è semplice: nel sistema di riferimento del muro io vado a velocità enorme e ho un’enorme energia cinetica. Ma lo stesso capita anche nel mio sistema di riferimento: io vedo il muro che mi viene incontro con un’enorme velocità e quindi con un’enorme energia cinetica. In entrambi i sistemi di riferimento la catastrofe è la stessa! Non perdiamo mai di vista il succo più profondo di tutta la RR, anche quando nella dinamica acquista un significato fisico ben più evidente.
Purtroppo, mi accorgo, girando qua e là, che questa semplice descrizione risulta ancora di difficile comprensione. Temo che il problema nasca dalla troppo normale e ambigua frase: “Per chi viaggia a grande velocità il tempo si dilata”. DOVREBBE ESSERE ABOLITA DA TUTTO E DA TUTTI. Molti capiscono che l’orologio del viaggiatore vada veramente più piano. Ciò non è assolutamente vero. Il suo orologio gira più lentamente solo per chi lo osserva da un altro sistema di riferimento… Tutti gli orologi girano nello stesso modo se osservati nel sistema in cui sono posizionati, perfino quello del … fotone. La dilatazione si ha solo cambiando sistema e guardando quello degli altri…
Io spero veramente che chi ha seguito con pazienza e molta calma le nostre tappe di avvicinamento ai risultati più eclatanti della RR abbia veramente compreso i concetti fondamentali e non abbia bisogno di saltare da uno youtube a un altro per cercare di convincersi di aver capito qualcosa che non ha mai studiato e, quindi, mai veramente compreso... E che poi porta a credere e a scrivere che "invecchia meno soltanto chi ha veramente viaggiato a grande velocità...". ASSURDO, ASSURDO!!!
Mai, come nella RR, sono più che sufficienti un foglio di carta e un matita... Senza dimenticare che Celestia, Stellarium e cose del genere non potrebbero dare nessun aiuto a chi vive solo di programmi prefabbricati...
E non ditemi che osservare nebulose, galassie, stelle doppie, craterini lunari sia un segno nitido e chiaro della passione per l'astrofisica e per l'Universo. E nemmeno che sia più facile rigirarsi tra sigle e codici di oculari e di lenti di Barlow che capire la relatività della simultaneità (la base di tutta la RR).
Il tutto nasconde solo pigrizia e voglia di emergere, a tutti i costi, anche se si è piccoli piccoli... In realtà, comprendere la RR vuol SOLO dire capire come funziona l'Universo nelle sue parti più intime, mentre fare una foto modestissima di una galassia che Hubble ci ha mostrato in tutti i suoi particolari o far girare Stellarium meglio del vicino di casa, ti fa sentire veramente importante!
Cari amici... lentamente ci stiamo arrivando... RR, MQ e RG, le tre basi fondamentali per affacciarsi all'Universo e poter dire di conoscere chi stiamo guardano. Poco importa se poi ci si dimentica di alcune formule: l'importante è che si sia compresa l'anima di quelle stupende creature e non solo la loro sbiadita immagine esteriore. Questa è in fondo la vera differenza tra un appassionato e un banale astrofilo da sigle e codici vari o da stellarium & co. Un volta che si è compresa l'anima, il potere ammirare con un qualsiasi pezzo di vetro e/o cercare di aggiungere le proprie emozioni più vere a quelle degli "amici" così lontani, diventano opere degne e appaganti (come la nostra Giorgia ci insegna...).
Ricordiamoci sempre che RR e MQ non possono essere difficili, dato che i nostri più intimi mattoncini le usano normalmente e costantemente...
E se qualcuno ancora non fosse convinto che la RR descrive eventi reali e non solo casi teorici, può fare la conoscenza dei simpatici e un po' sfortunati muoni.
Dall'energia alla massa
Le abbiamo studiate un po’ tutte, anche partendo solo dalla massa relativistica. Vale la pena, comunque, fare il procedimento inverso, ossia dare per acquisita la formula dell'energia a riposo e vedere se, manovrandola adeguatamente, troviamo la massa relativistica.
Qualcuno potrebbe dire: “E’ ovvio!”, ma in fisica non è mai inutile svolgere i processi inversi, dato che spesso si scoprono relazioni di grande interesse. E, poi, è pur sempre esercizio utile per il cervello.
Partiamo, quindi, ammettendo che un certo signor Einstein abbia concluso, sognandolo di notte, che:
E0 = m0c2 …. (22)
Non ci resta che far muovere il corpo applicandogli una forza e vedere cosa succede. Ovviamente, se il corpo si muove deve acquisire energia cinetica, per cui l’energia del corpo deve aumentare. Dato che l’energia del corpo fermo è uguale a una massa moltiplicata per una costante, è ovvio che deve aumentare la massa.
Sì, ma come?
Sappiamo che la variazione di energia, dovuta all’azione di una forza su un corpo, è data da:
dE/dt = F v
Abbiamo già incontrato questa formula, che è quella che ci regala il lavoro svolto da una forza nell’unità di tempo. Ricordate la potenza?
P = L/t = F s/t = F v
Ma il lavoro non è altro che una differenza di energia in un certo intervallino di tempo e, quindi:
dE/dt = F v …. (23)
In realtà, dovremmo usare vettori e prodotto scalare tra vettori, ma se la forza agisce nel verso del movimento possiamo limitarci ai moduli.
Sappiamo, però, anche che:
F = d(mv)/dt
La (23) diventa, ricordando la (22) (non siamo più a riposo e m0 deve essere aumentata, come già detto prima)
d(mc2)/dt = v d(mv)dt
Tutto quello che dobbiamo fare è risolvere questa equazione, ricavando la massa. Abbiamo bisogno di qualche trucchetto…
Moltiplichiamo entrambi i membri per 2m:
c2 2m d(m)/dt = 2mv d(mv)dt …. (24)
Non sbagliamo di certo se ricordiamo che 2m d(m)/dt non è altro che la derivata di m2:
d(m2)/dt = 2m dm/dt
ma, analogamente, vale anche:
d(mv)2/dt = 2mv d(mv)/dt
Sostituendo nella (24):
c2 d(m2)/dt = d(m2v2)/dt
Basta fare l’integrale indefinito di entrambi i membri e abbiamo
m2 c2 = m2v2 + k .... (25)
Stiamo parlando di integrali indefiniti e quindi ci dobbiamo portare dietro una costante…
Tuttavia, la relazione precedente deve essere valida per qualsiasi velocità, quindi anche per v = 0…
Essa diventa:
m02c2 = 0 + k
La costante è quindi determinata e vale:
k = m02 c2
Possiamo allora sostituire k nella (25) che diviene:
m2(c2 – v2) = m02 c2
m2 = m02c2/(c2 – v2) = m02/(1 – v2/c2)
e, infine:
m = m0/(1 – v2/c2)1/2
come volevasi dimostrare… e, intanto, abbiamo ripassato un po' di derivate e integrali...
Massa ed energia si conservano insieme
Siamo partiti con un urto elastico e poi abbiamo anche visto cosa capita in un urto anelastico, dove le masse a riposo, con una certa sorpresa, non si sono conservate nell’urto. La faccenda, però, è ormai abbastanza chiara: se non si conserva la massa ci pensa l’energia a mettere tutto a posto, dato che sono praticamente la stessa cosa. Questo esercizio riveste un’importanza veramente fondamentale per comprendere al meglio la rivoluzione einsteniana.
Analizziamo nuovamente, con particolare attenzione, un caso semplicissimo: l’urto frontale anelastico, lo stesso attraverso cui avevamo trovato che M0 > 2m0.
Nel sistema di riferimento S’, due corpi A e B, di pari massa a riposo m0, viaggiano uno contro l’altro con velocità u’0 come mostrato in Fig. 13.
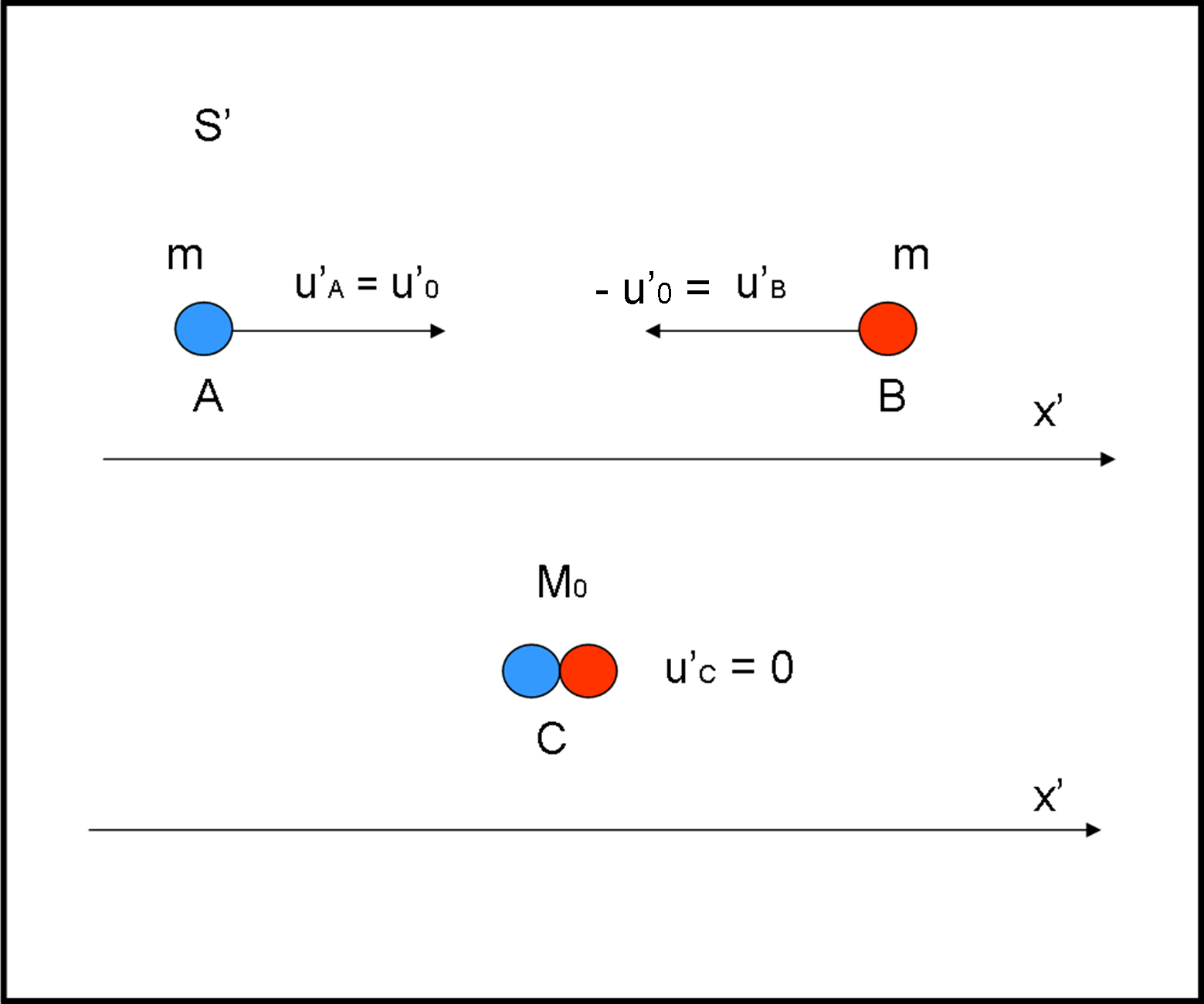
Vale, ovviamente:
u’A = u’0
e
u’B = - u’0
L’urto che avviene è completamente anelastico e dopo l’urto i due corpi viaggiano uniti (corpo C) con massa M e con una certa velocità u’C. Per la conservazione della quantità di moto relativistica, devono coincidere le quantità di moto prima e dopo l’urto.
Prima dell’urto:
m0 γ (u’A) u’A + m0 γ (u’B) u’B = m0 γ (u’0) u’0 - m0 γ (u’0) u’0 = 0
Dopo l’urto:
M u’C = 0
Da cui si ricava che u’C = 0.
Il corpo C, unione dei due corpi A e B, rimane fermo e la sua massa è quella a riposo M0.
Nella fisica classica sappiamo che M0 = 2m0 e che l’energia cinetica NON si conserva, dato che prima dell’urto vale 2 ½ mu'02 e dopo l’urto vale 0. Abbiamo la conservazione della massa, ma non dell’energia cinetica.
Vediamo cosa succede in campo relativistico. Già ci dobbiamo aspettare che M0 > 2m0, ma c’interessa sapere cosa fa l’energia cinetica. Per cui rifacciamo il calcolo in un caso più generale.
Non ci resta che cambiare sistema di riferimento. La conservazione della quantità di moto deve, comunque, restare valida e a noi non resta che sfruttarla.
Consideriamo un sistema S in cui il corpo B risulti fermo (Fig. 14).
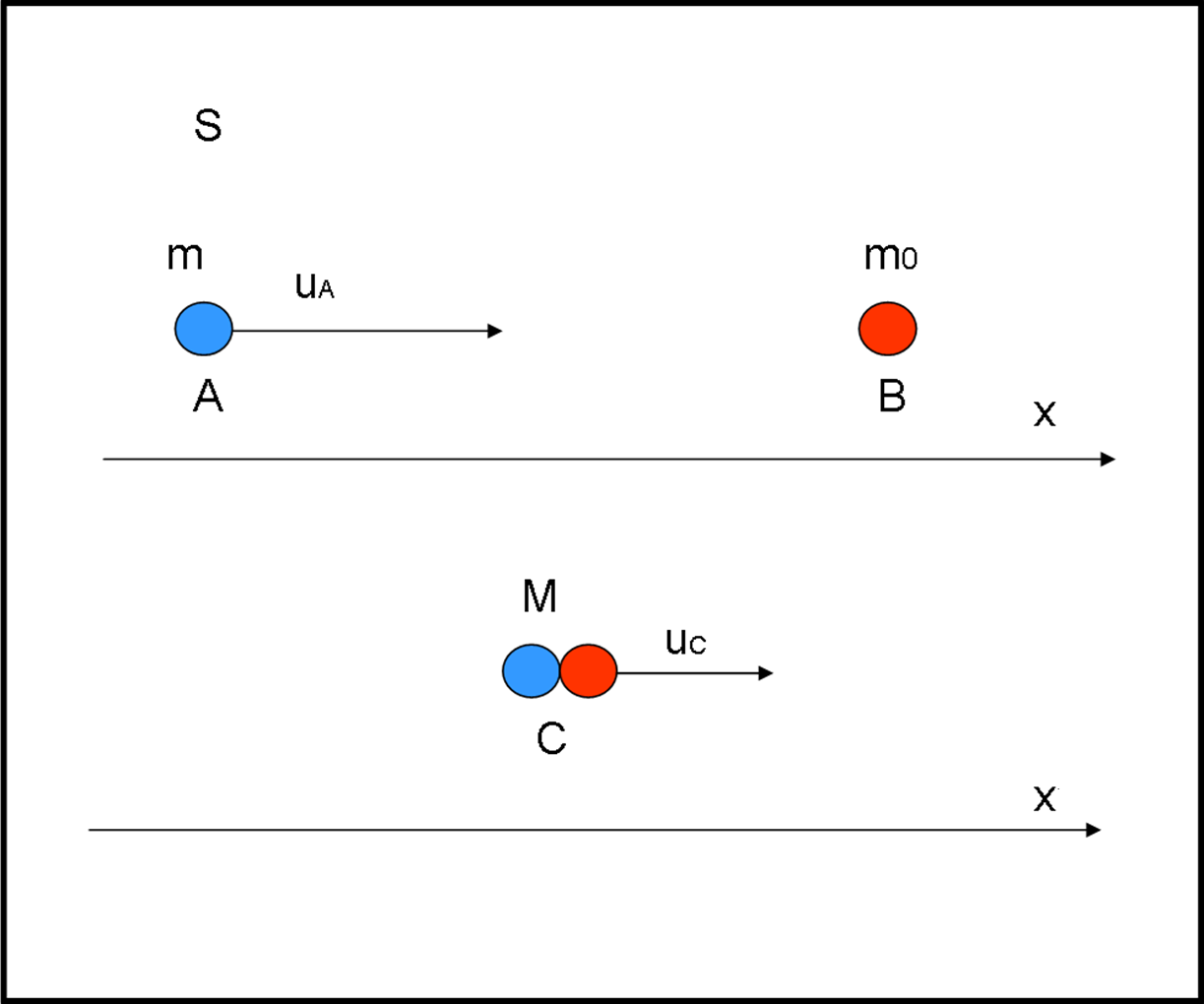
Ossia
uB = 0
Esso vedrà S’muoversi con una velocità di trascinamento v = u’0 (S si muove con velocità – u’0 rispetto a S’).
Calcoliamo, ora, le velocità uA e uC, attraverso la ben nota formula di composizione relativistica delle velocità:
u = (u’ + v)/(1 + u’v/c2) (formula generale, tanto per richiamarla…)
Nel nostro caso:
uA = (u’A + v)/(1 + u’A v/c2) = (u’0 + u’0)/(1 + u’0 u’0/c2) = 2u’0/(1 + u’02/c2) …. (26)
uC = (u’C + v)/(1 + u’C v/c2) = 0 + u’0/(1 + 0·u’0/c2) = u’0 …. (27)
Per la conservazione della quantità di moto nel sistema S deve allora essere:
m0 γ(uA) uA + m0 γ(uB) uB = M0 γ(uc) uC
e quindi:
m0 γ(uA) uA + 0 = M0 γ(u’0) u’0
m0 uA/(1 – uA2/c2)1/2 = M0 u’0/(1 – u’02/c2)1/2
Non ci resta che sostituire la uA trovata con la (26)…
Sono passaggi algebrici semplici e un po’ noiosi, ma fanno molto bene come esercizio. Li lascio a voi! Il risultato comunque è:
2 m0 u’0/(1 – u’02/c2) = M0 u’0/(1 – u’02/c2)1/2
Da cui:
2 m0 /(1 – u’02/c2)1/2 = M0 ….(28)
E, quindi:
M0 > 2m0
Come già trovato nell’articolo passato: le masse a riposo non si conservano.
Dalla uguaglianza tra massa ed energia, la relazione (28) ci dice, però, che anche l’energia a riposo del corpo C di massa M0 è maggiore delle energie a riposo della somma delle masse a riposo di A e B. Infatti basta moltiplicare a sinistra e a destra per c2 per avere le energie a riposo.
M0c2 > 2m0c2
Tuttavia, la stessa relazione (28) ci dice anche che l’energia totale del sistema si è conservata nell’urto.
Consideriamo nuovamente il sistema S’, dove le due masse A e B andavano una contro l’altra e formavano una massa C immobile.
In questo sistema l’energia totale prima dell’urto (EP) è data dalla somma delle due energie totali di ogni particella.
EPA = EPB = mc2 = m0γ(u’0) c2
EP = EPA + EPB = 2m0γ(u’0)c2 = 2m0 c2/(1 – u’02/c2)1/2
Dopo l’urto, l’energia totale ED non è altro che quella a riposo di C
ED = M0c2
Ma, sostituendo al posto di M0 la relazione (28), si ottiene.
ED = 2 m0 c2/(1 – u’02/c2)1/2
E, quindi:
EP = ED
Anche negli urti anelastici l’energia totale si conserva!
In conclusione, partendo dalla legge di conservazione della quantità di moto relativistica, si ottiene che l’energia totale del sistema si conserva in qualsiasi sistema di riferimento inerziale. Al contrario di quanto avveniva in meccanica classica, in qualunque tipo di urto si deve conservare sia la quantità di moto relativistica che l'energia relativistica.
Riassumendo: la conservazione dell'energia rappresenta una legge valida per qualunque fenomeno fisico e vale in qualunque riferimento inerziale, in accordo con il principio di relatività.
Il “succo” fisico di questo esperimento è ormai facilmente comprensibile: le masse a riposo non si conservano così come le energie cinetiche, ma si conserva l’energia totale. Una dimostrazione lampante e decisiva che massa ed energia sono la stessa cosa!
Che dire? Un risultato sconvolgente nella sua semplicità e nella sua importanza rivoluzionaria. Non possiamo che considerare la teoria della relatività ristretta un vero capolavoro assoluto (qualcosa di … assoluto c’è!). Non ci resta che ammirarlo, come la Gioconda, ma sapendo finalmente cosa vuole rappresentare (non è una foto ben riuscita di un viso sorridente, ma la Natura che prende coscienza di se stessa).
Ancora un passo (forse ancora più fondamentale) e poi possiamo riposarci un po’…
Riflettiamo
Poche parole di intermezzo, prima del salto finale. Una piccola difesa delle formule che appaiono costantemente e un invito a ragionare su scala più ampia e comprendere come tutto sia stato veramente semplice, partendo solo e soltanto da qualche orologio sincronizzato e qualche asta rigida. Ricordate Einstein e Newton davanti alla commissione d’esame? Eravamo proprio all’inizio della relatività ristretta…
Gli articoli che sono apparsi finora hanno fatto uso di parecchia matematica (anche se non trascendentale) con lo scopo di mostrare come ogni relazione sia strettamente legata alle altre e come tutto, in fondo, giochi sull’insostituibile fattore gamma.
Tuttavia, non dimentichiamo i concetti fondamentali che siamo riusciti a ottenere. Essi vanno ben oltre una matematica più o meno ripetitiva, ma creano le basi di tutta la fisica moderna. Abbiamo cercato di accontentare chi ha voglia di toccare con mano ogni singolo passaggio, ma anche chi vuole estrarre i concetti decisivi e rivoluzionari, sapendo però che non vengono consegnati dall’alto, ma attraverso un’attenta lettura delle poche nozioni di base.
Ragioniamoci un po’ sopra… Abbiamo sbattuto la testa contro la relatività della simultaneità, pensando di trovarci di fronte a un fenomeno apparente e lontano dalla realtà. Poi ci siamo accorti che questo modo di ragionare ci portava a vedere orologi rallentare e lunghezze contrarsi. Tutte cose che dipendono dall’osservatore, ma che rappresentano la realtà, anche se non visibile con i ritmi umani. I muoni, però, ci hanno avvertito chiaramente, così come il diagramma di Minkowski ci ha illustrato come questa “visione” relativistica possa creare un quadro logico e generale dell’intero spaziotempo. Anzi, è in grado di creare proprio lo spaziotempo in cui può esprimersi l’Universo.
Dalla pura cinematica siamo passati, senza alcuna difficoltà reale, alla dinamica e a concetti di portata ben più ampia, quali la quantità di moto e l’energia cinetica. Basandoci sulla meccanica classica, quasi senza accorgersene, l’applicazione dei principi della RR ha portato a una rivoluzione stupefacente: la massa e l’energia sono diventate la stessa cosa!
Gli stessi fotoni acquistano una nuova vita e così tutti i loro amici capaci di avvicinarsi a velocità per noi impossibili. Come la nebbia si scioglie al Sole, così la chimica e la fisica nucleare diventano ovvie conseguenze di quella apparentemente assurda relatività della simultaneità. Pensiamoci sopra e ci accorgiamo che tutto nasce da lì… da una visione geniale di qualcosa che è sotto gli occhi di tutti: basta ragionare senza temere di allontanarsi apparentemente dalla realtà.
Sì, la trasformazione di Lorentz c’era già, così come le leggi di Maxwell che imponevano una costanza della velocità della luce. Ma nel giro di poche settimane Einstein è riuscito a far nascere una teoria universale che non aveva praticamente alcuna possibilità di essere verificata a quei tempi, ma poteva solo aspettare il futuro.
Una teoria estremamente semplice che siamo riusciti a seguire senza grande fatica. Possiamo anche dimenticare molte formule, ma non la sequela dei processi che ci hanno portato alla formula più famosa del mondo. Possiamo dire, con un certo orgoglio, che NOI l’abbiamo capita e ricavata, senza limitarsi a prenderla come una pillola per curare un raffreddore.
Non arrabbiamoci, quindi, se stiamo esagerando con le formule matematiche e con giri a destra e a sinistra, sopra e sotto. Quando si ha un giocattolo nuovo, che sappiamo finalmente usare completamente, è difficile stancarsi…
Questa è la RR, una meraviglia che si scrive quasi da sola, capendo da cosa partire…
Ben più difficile è stata la conquista della relatività generale, contro cui Einstein ha sbattuto la testa a lungo e che ha dovuto affrontare attaccandola da più parti. Non più settimane, ma anni per averne finalmente ragione. Oggi, sappiamo che si può spiegare più facilmente di quanto abbia fatto lo stesso Einstein, ma solo lui poteva giungere alla fine, senza paura alcuna di accettare una “curvatura” dello spaziotempo creato con la RR.
Non lamentiamoci, quindi, delle formule (che potremo anche dimenticare)… ma pensiamo ai concetti che abbiamo raggiunto un po’ alla volta con umiltà e perseveranza. Facciamo un breve riassunto mentale e ci sentiremo fieri di noi stessi. Anche questa emozione è umiltà culturale!
Un altro invariante
Fatemi arrivare al dunque in modo molto personale e “quasi” allegro e spontaneo. Abbiamo incontrato lungo il percorso nuove grandezze che dipendono dalla velocità. Grandezze che cambiano, cambiando sistema di riferimento. Ciò che viene conservato sono le loro leggi di … conservazione. D’altra parte siamo o non siamo nella relatività ristretta? Tuttavia, pensandoci bene, qualcosa che non cambia c’è e questo fatto implica un nuovo invariante che lega l’energia con la mia grandezza preferita.
Una grandezza che non varia, cambiando sistema, è veramente ovvia: l’energia a riposo di una certa massa (a riposo) m0. Essa è il prodotto tra la massa a riposo (che è quella che è ovunque) e il quadrato di una costante che più costante non si può: la velocità della luce c.
Sì, va bene… ma è poca cosa, in realtà. Sarebbe molto meglio trovare qualcosa di più articolato che contenga sia l’energia totale (e quindi la massa relativistica) sia la mia tanto amata quantità di moto (giuro che non sono stato io a suggerirlo a Einstein, ha fatto tutto da solo…).
Una cosa complicata? Nemmeno per sogno, l’abbiamo già tra le mani, basta scriverla nel modo giusto.
Tanto per cambiare, partiamo dalla massa relativistica:
m = m0/(1 - v2/c2)1/2
Tuttavia, volendo far comparire le energie è molto meglio elevare a quadrato:
m2 = m02/(1 - v2/c2) = m02 c2/(c2 - v2)
e, ancora:
m2(c2 - v2) = m02c2
Per far comparire le energie dobbiamo ancora moltiplicare entrambi i membri per c2 e si ottiene:
m2c4 - m2v2c2 = m02c4
m2c4 = m02c4 + m2v2c2
Attenzione, però:
m0c2 è l’energia a riposo E0
mv e la quantità di moto relativistica q
mc2 è l’energia totale E
La relazione di prima ci dice che l’energia totale E risulta uguale a:
E2 = E02 + q2c2
Essa crea un legame indissolubile tra energia totale, energia a riposo e quantità di moto. La sua importanza è di carattere sia pratico (è meglio lavorare in termini di energia e quantità di moto che non direttamente con le masse) che teorico (accenneremo soltanto a una fantastica conseguenza…).
Ancora più rivoluzionaria è la stessa espressione scritta così:
E02 = E2 - q2c2 …. (29)
Perché è cosi importante? Presto detto: il primo membro è una quantità che risulta invariante per qualsiasi sistema di riferimento inerziale (è l'energia a riposo). Deve perciò esserlo anche il secondo membro, ossia:
E2 – q2c2 = costante
Abbiamo trovato un’altra grandezza che è un invariante relativistico, al pari dell’ormai celebre distanza relativistica s2 (ricordate Minkowski, dopo la Fig. 19 ?). Dimostreremo anche, malgrado sembri quasi impossibile, la perfetta similitudine tra s2 e E2 – q2c2 .
Cominciamo a notare (ma ci torneremo sopra) che:
s2 = t2c2 – d2 …. (30)
dove d è la distanza spaziale classica:
d2 = x2 + y2 + z2
Notiamo ancora che x, y, z possono essere considerate le componenti del vettore spazio d, mentre t è uno scalare. Parlando di Minkowski avevamo considerato solo la componente x e avevamo posto T = ct, ma la formula è sempre la stessa. In quel caso avevamo scritto:
s2 = T2 – x2
che è esattamente la (30).
Nel nuovo invariante, abbiamo di nuovo un vettore (quantità di moto q, con le sue tre componenti) e uno scalare (energia E).
Ma...ci torneremo sopra tra non molto. Ogni cosa a suo tempo.
Torniamo, momentaneamente, alla (29) e notiamo come possa essere interessante descrivere attraverso un grafico la relazione tra q ed energia E. La funzione da studiare è:
q = (E2 – E02)1/2/c
Potete provarci tranquillamente voi, prima di proseguire. Il tutto si riduce, in fondo, a trovare un asintoto obliquo (un bell’esercizio per non dimenticare la … matematica)
Ovviamente, per q = 0, abbiamo E = E0
Mentre l’asintoto ha equazione
q = E/c
Il grafico è quello rappresentato in Fig. 15
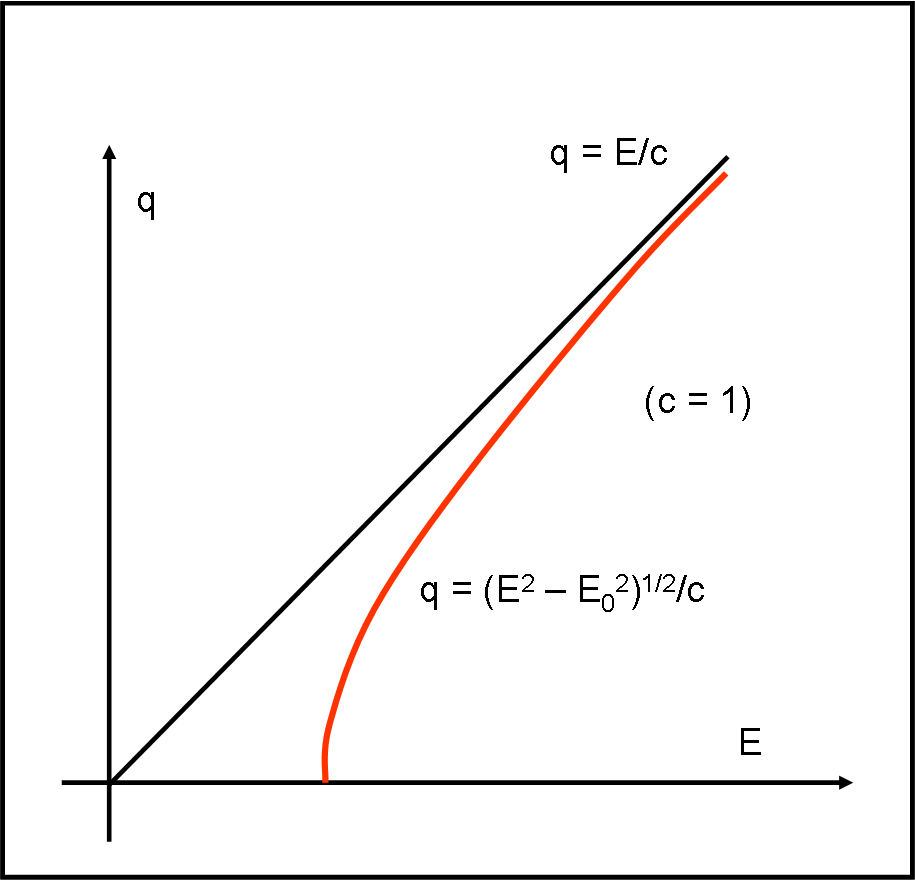
in campo ultrarelativistico abbiamo che E0 è del tutto trascurabile e si ha:
E ~ qc
L'energia è, in pratica, nient'altro che la quantità di moto (con le dovute unità di misura).
Il vuoto quantistico
Diamo solo un piccolo assaggio di quello che un giorno vorrei descrivere con molta calma e attenzione. Un legame strettissimo tra relatività ristretta e meccanica quantistica che ha portato a conseguenze quasi impensabili. Così, un piccolo stuzzichino, tanto per gradire...
Riprendiamo ancora la:
E2 = E02 + q2c2
La relazione ci dice che ci sono due modi per cambiare l’energia di un corpo:
1) Cambiare la quantità di moto, senza toccare l’energia a riposo. In altre parole, agendo sulla velocità del corpo rispetto al sistema di riferimento.
2) Cambiare l’energia a riposo. Il che vuole dire cambiare la massa a riposo. Impossibile? Assolutamente no, nel campo delle particelle che vivono in ambito relativistico. Basta pensare alla fissione nucleare e all’annichilazione di materia e antimateria.
Cari amici, la RR permette di studiare a fondo la vita dell’infinitamente piccolo e dà una mano fondamentale alla meccanica quantistica. Guai a snobbarla, Einstein si arrabbierebbe non poco e altro che … lingua ci farebbe!
Concludiamo questa parte con una riflessione che apre veramente una porta non solo sull’Universo, ma -forse- anche su quello che … c’era prima!
Riprendiamo ancora in mano la solita relazione:
E2 = E02 + q2c2
Essa, con molta leggerezza, porta subito a:
E = (E02 + q2c2)1/2
Ma non ci siamo dimenticati qualcosa? Quando si esegue una radice quadrata i risultati sono sempre due, uno col segno più e uno col segno meno! Perché allora non considerare anche la soluzione:
E = - (E02 + q2c2)1/2
Non siamo ancora pronti per entrare nel fantastico mondo che si nasconde dietro questa semplicissima formula. Tuttavia, basta dire poche frasi buttate lì… sulle quali speriamo di poter tornare con ben maggiore attenzione.
Può esistere l’energia negativa e questa non ha alcun limite inferiore. Essa può essere dominio dell’antimateria. Inoltre, possiamo supporre che tutti gli stati a energia negativa (i più ambiti, in fondo) siano occupati. Ne consegue che lo stato fondamentale, il cosiddetto “vuoto”, non è altro che un mare di particelle sistemate negli stati negativi dell’energia.
Fermi tutti… sarebbe troppo semplice. Abbiamo bisogno di costruirci un salvagente molto speciale, perché stiamo per tuffarci nel mare di Dirac, nel vuoto-non vuoto quantistico, dove regna sovrano il principio di Pauli. Niente può, perciò, trovare posto in questo mare, completamente occupato. Tuttavia, se una particella è costretta a lasciare libero uno stato a energia negativa, spinta via da un fotone molto energetico, nasce una particella normale, a energia positiva. Il posto lasciato libero assume le sembianze della particella scappata ma con carica opposta. Questione di un attimo e un lampo di energia ci assicura che il posto tanto ambito viene nuovamente occupato. Particella e antiparticella si sono annichilite. (Ricordate la parte finale della QED, dopo Fig. 57 ?).
Il discorso è, ovviamente, molto più complesso e articolato, ma … qualcuno osa ancora dire che si può fare a meno di quel capolavoro assoluto che è la relatività ristretta?
No, in questo circolo, penso proprio di no!
Gli invarianti si scrivono nello stesso modo
Potremmo fermarci qui. Tuttavia, non è male verificare la perfetta somiglianza dei due invarianti relativistici incontrati.
Partiamo proprio da lontano, dalle trasformazioni di Lorentz, in cui scriviamo le coordinate di un evento visto da un sistema S’, che si muove con velocità u, rispetto al sistema considerato fisso S, lungo l’asse x. Le formule sono:
x’ = (x – ut)/(1 – u2/c2)1/2
y’ = y
z’ = z
t’ = (t – ux/c2)/(1 – u2/c2)1/2
Sappiamo che, scegliendo in modo acconcio le unità di misura, si può ottenere c = 1.
Risulta:
x’ = (x – ut)/(1 – u2)1/2
y’ = y
z’ = z
t’ = (t – ux)/(1 – u2)1/2
Noi avevamo posto T = ct (T’ = ct’), ma le cose non cambiano (nel caso, andatevi a rileggere le lezioni sulla basi della relatività speciale QUI) e continuiamo a scrivere t invece di T, pur considerando c = 1. E’ solo un problema di simboli…
Il tempo era diventato una coordinata del tutto simile a quelle spaziali ed eravamo passati dal concetto di punto al concetto di evento, definito da tre coordinate spaziali e da una temporale.
Avevamo poi dimostrato che la classica distanza tra due punti non si conservava nella relatività speciale, ma esisteva una speciale “distanza” che restava sempre la stessa in tutti i sistemi di riferimento (l’invariante spaziotemporale).
Lo avevamo chiamato s2 ed era stato definito come:
s2 = t’2 – x’2 – y’2 – z’2 = t2 – x2 – y2 – z2
Attraverso di lui Minkowski si era divertito a creare il suo Universo e molte altre cose.
Per maggiore chiarezza, noi avevamo solo considerato la componente x ( e x’) e la t ( e t’) in quanto lavoravamo solo nel piano x,t (x’,t’), ma il passaggio allo spaziotempo a quattro dimensioni è cosa più che intuitiva.
Cosa abbiamo fatto, in parole povere? Abbiamo associato a un vettore con tre componenti (in questo caso quello che definisce la posizione di un punto rispetto, ad esempio, all’origine) uno scalare che possiamo chiamare componente temporale. Questa grandezza a quattro dimensioni la chiamiamo quadrivettore. Come il vettore è rappresentabile con d(x,y,z) così il quadrivettore è rappresentabile con R(x,y,z,t).
Come per il vettore (chiamiamolo pure trivettore) la distanza d(x,y,z) definisce una distanza invariante nello spazio a tre dimensioni (cambiano le singole coordinate, ma non d2 = x2 + y2 + z2), così per il quadrivettore R(x,y,z,t) nello spaziotempo a quattro dimensioni si definisce una “distanza” invariante s2 = t2 –x2 –y2 – z2. Quante interessanti riflessioni ci ha permesso di fare questa semplice “distanza” un po’ speciale (QUI)…
Esistono altri quadrivettori nello spaziotempo relativistico? Sicuramente sì. Uno lo abbiamo appena trovato ed è quello che ha come componenti quelle del vettore quantità di moto e come scalare l’energia.
In poche parole è un quadrivettore R(qx, qy, qz, E), così come quello spaziotemporale era R(x, y, z, t).
Scriviamo di nuovo l’invariante a lui associato:
E2 – q2c2 = costante
Imponiamo di nuovo, per analogia, che c sia proprio uguale a 1.
Allora, possiamo scrivere:
E = mc2 = m = m0/(1 – v2)1/2
E2 = m02/(1 – v2)
q = mv = m0v/(1 – v2)1/2
q2 = m02v2/(1 – v2)
Da cui:
E2 – q2 = m02/(1 – v2) - m02v2/(1 – v2) = m02(1 – v2)/(1 – v2) = m02
Ricapitoliamo:
E = m0/(1 – v2)1/2 …. (31)
q = m0v/(1 – v2)1/2 …. (32)
da cui l’invariante:
E2 – q2 = cost. = m02 …. (33)
Tra l’altro abbiamo anche una relazione poco usata ma molto interessante (anche se facile da ricavare):
q = E v …. (34)
Non è difficile da interpretare. La quantità di moto relativistica è la massa relativistica moltiplicata per la velocità. Ma la massa relativistica non è altro che l’energia (avendo posto c = 1). Segniamocela.
Semplifichiamo la situazione, come già fatto nella RR, e consideriamo un sistema S’ che si muova rispetto a S con velocità u lungo x, il che vuol dire che il sistema S si muove rispetto a S’ con velocità – u. La velocità u abbia la stessa direzione di v. Ciò vuol dire, in pratica, che possiamo considerare come quantità di moto solo la sua componente lungo questa direzione. Continuiamo a chiamarla q invece di qx, Valgono, perciò, le relazioni precedenti. Trascuriamo le componenti secondo x e y dato che non subiscono trasformazioni (e secondo qy e qz).
Vogliamo determinare le trasformazioni tra E e E’ e tra q e q’ (come fatto per t e t' e per x e x'). Ci accorgeremo che la loro scrittura diventa veramente immediata…
Ovviamente, bisogna anche verificare che:
E’2 – q’2 = E2 – q2
Risolviamo il problema delle trasformazioni e ci accorgiamo che le formule sono esattamente le stesse che avevamo ottenuto trasformando t in t’ e x in x’, ossia le equazioni:
x’ = (x – ut)/(1 – u2)1/2
t’ = (t – ux)/(1 – u2)1/2
diventano
q’ = (q – uE)/(1 – u2)1/2
E’ = (E – uq)/(1 – u2)1/2
In poche parole, le trasformazioni tra quantità di moto ed energia sono esattamente le stesse che si hanno tra lo spazio x e il tempo t. Basta inserire l’energia al posto del tempo (scalare) e la quantità di moto al posto di x (componente di un vettore).
Partiamo dalle due banali e ben note relazioni ((31) e (32))
E = m0/(1 – v2)1/2
q = m0v/(1 – v2)1/2
Come possiamo notare, entrambe contengono v, la velocità nel sistema S. Quello che vogliamo fare è calcolare E’ e q’ come vengono misurate in un sistema S’, dove la velocità è v’. La solita vecchia storia della RR.
E’ = m0/(1 – v’2)1/2
e
q’ = m0v’/(1 – v’2)1/2
Non ci resta che far comparire a secondo membro le velocità v relativa a S e la velocità di trascinamento di S’ rispetto a S (u), nello stesso identico modo in cui nelle trasformazioni di Lorentz facevamo comparire t e x per esprimere x’ e t’.
Ancora una volta, non dobbiamo fare altro che eseguire una composizione di velocità lungo l’asse delle x. Ormai la formula necessaria è diventata nostra carissima amica… (ricordiamo che c = 1).
v’ = (v – u)/(1 – uv)
Cominciamo a scrivere la parte sotto radice quadrata, ossia (1 – v’2)…
Iniziamo con fare il quadrato di v’:
v’2 = (v – u)2/(1 – uv)2 = (v2 + u2 – 2uv)/(1 + u2v2 – 2uv)
E poi cambiare di segno e aggiungere 1 (e portare tutto allo stesso denominatore):
1 – v’2 = 1 - (v2 + u2 – 2uv)/(1 + u2v2 – 2uv) = (1 + u2v2 – 2uv – v2 – u2 + 2uv)/(1 + u2v2 – 2uv)
1 – v’2 = (1 + u2v2 – v2 – u2)/(1 + u2v2 – 2uv)
1 – v’2 = ((1 – v2) – u2(1 – v2))/(1 – uv)2 = (1 – v2)(1 – u2)/(1 – uv)2
Bene. Adesso mandiamo tutto al… denominatore e facciamo la radice quadrata:
1/(1 – v’2)1/2 = (1 – uv)/((1 – v2)1/2(1 – u2)1/2) …. (35) (ci servirà dopo ….)
Non ci resta che moltiplicare per la massa a riposo m0, che rimane sempre la stessa in ogni sistema di riferimento:
E’ = m0/(1 – v’2)1/2 = m0(1 – uv)/((1 – v2)1/2(1 – u2)1/2) = (m0 – m0uv)/((1 – v2)1/2(1 – u2)1/2)
Mamma mia… è stata abbastanza dura e, inoltre, sembra di essere ben lontani dal risultato voluto! Calma e sangue freddo. Divertiamoci un po’ con la matematica. Scriviamo la stessa cosa in modo apparentemente ancora più complicato:
E’ = ((m0/(1 – v2)1/2) – (m0uv/(1 – v2)1/2))/(1 – u2)1/2 …. (36)
Avete eseguito con calma i vari passaggi? Bene. Adesso non è difficile sostituire alle varie parti quello che rappresentano.
Ad esempio:
m0/(1 – v2)1/2 = E
Inoltre:
m0uv/(1 – v2)1/2 = uq
Non ci resta che sostituire nella (36) e si ottiene, quasi miracolosamente:
E’ = (E – uq)/(1 – u2)1/2
Non è difficile confrontarla con la ben più celebre:
t’ = (t – ux)/(1 – u2)1/2
Esattamente quello che avevamo preannunciato: per trasformare E in E’ basta sostituire nella formula precedente t con E, t’ con E’ e x con q. E il gioco è fatto!
Scommettiamo che ormai siete più che sicuri che lo stesso succederà anche con q’? Di Einstein ci si può fidare… Comunque, eseguiamo ancora qualche calcoletto divertente… La faccenda è molto più semplice.
Sappiamo dalla (34) che:
q’ = E’ v’
basta sostituire E’, utilizzando la (35) moltiplicata per m0, e la v’ in funzione di v e u.
q’ = m0(1 – uv)/((1 – v2)1/2(1 – u2)1/2) (v – u)/(1 – uv)
Semplificando tra numeratore e denominatore si ha:
q’ = m0 (v – u)/((1 – v2)1/2(1 – u2)1/2) = (m0v – m0u)/((1 – v2)1/2(1 – u2)1/2)
Scriviamolo in modo più… utile:
q’ = m0v/((1 – v2)1/2(1 – u2)1/2) - m0u/((1 – v2)1/2(1 – u2)1/2)
Ma, sappiamo ormai molto bene, dalla (31), che:
m0v/(1 – v2)1/2 = q
e, dalla (32) che:
m0/(1 – v2)1/2 = E
Ne segue:
q’ = q/(1 – u2)1/2 – uE/(1 – u2)1/2
q’ = (q – uE)/((1 – u2)1/2
del tutto analoga a:
x’ = (x – ut)/(1 – u2)1/2
Sì, è vero, è stata un po' dura, ma, in fondo, sono stati passaggi di semplice matematica, alla portata di tutti o quasi.
Non andremo oltre, ma possiamo facilmente immaginare le fantastiche possibilità pratiche. Ciò che sembrava un espediente matematico e geometrico, ci permette di descrivere graficamente l’energia e la quantità di moto in un diagramma di Minkowski, in accordo con le equazioni di Lorentz. Non solo spazio e tempo che si contraggono e si dilatano, ma grandezze di assoluta importanza fisica come energia e quantità di moto.
Abbiamo anche imparato che nello spazio di Minkowski esistono almeno due grandezze che non variano nelle trasformazioni di Lorentz. Ma sono molte di più...
Concludiamo con il simpatico fotone
Permettiamoci ancora un piccolo “scherzo”, richiamando la particella più strana e più simpatica dell’Universo: il fotone.
Siamo sicuri che il fotone abbia massa a riposo uguale a zero?
Ricaviamolo in modo semplicissimo e ormai banale… ricordando che la velocità del fotone è uguale a c
Abbiamo:
E = mc2
m = E/c2
q = mc = Ec/c2 = E/c .... (37)
Scriviamo il nostro invariante
E2 - q2c2 = m02c4
Sostituendo la (37) al posto di q:
E2 – c2E2/c2 = m02c4
E2 – E2 = m02c4
0 = m02c4
Dato che c è sicuramente diversa da zero, deve essere zero la massa a riposo del fotone!
Tuttavia, Planck (QUI) ci ha insegnato che l’energia di un fotone non è assolutamente zero e così la sua quantità di moto. Anzi, esse sono la stessa identica cosa, dato che ponendo c = 1, come si può sempre fare usando le più comuni unità di misura dello spaziotempo, abbiamo proprio E = q (vedi equazioni precedenti).
Ma, allora, cosa capita a una particella che possiede sicuramente una certa energia (e non lo dice solo Planck, ma anche lo stesso Einstein con l’effetto fotoelettrico (QUI) e il non certo sprovveduto Sig. Compton (QUI)) quando si ferma? Scompare nel nulla? Assolutamente NO. Tutto si spiega molto semplicemente ricordando che il fotone non può mai stare fermo e deve correre sempre alla massima velocità possibile. Una strana creatura, davvero… Altro che papalatleta, lui esiste soltanto quando corre!
E non diciamo che è un assurdo, se si considera la relazione einsteniana dell’energia..
E = mc2 = m0c2/(1 - v2/c2)1/2
Sembrerebbe che per m0 = 0 anche l’energia debba fare lo stesso… E no! Come abbiamo già detto in una precedente lezione sulla dinamica relativistica, non possiamo dimenticarci che anche il denominatore va a zero, dato che v = c! E zero su zero non è affatto uguale a zero!
Leggiamo e rileggiamo la dinamica relativistica, senza disdegnare di tornare indietro alla cinematica. Tutto ha ormai assunto un’unità e una generalità meravigliose. Ribadiamolo ancora: le particelle infinitesimali, le uniche che possono avvicinarsi alla velocità della luce (e perfino raggiungerla), hanno trovato il grande narratore della loro eccezionale vita.
Viva la relatività speciale o ristretta (che di “ristretto” ha, in fondo, ben poco)!
Fusa di gatto Gualtiero che si trasformano in crocchette: questo e altro (tra cui anche qualcosa di serio) ci spiega Curiuss in "5 cose sconvolgenti contenute in E=mc2"






17 commenti
Se riesco a leggere questo articolo,poi me ne vado a insegnare al MIT in America
caro Gianni,
non sono altro che gli articoli della DR messi assieme... Conoscendoti già un po' sono sicuro che un passo alla volta ti troverai alla fine senza nessun problema...(detto fra noi, ho conosciuto un collega americano che insegnava planetologia al MIT e non sapeva la RR... ssssht!!!!)
Fidati, Gianni!
Nonostante le apparenze, la matematica utilizzata non va oltre quella della scuola media (basta ricordare che l'esponente 1/2 equivale alla radice quadrata) e, per aiutare la memoria, ci sono le lezioni di matematica dei miei amici PapalCaronte, PapalPotenza, PapalEstrattore e PapalMediatore. Non riesco ad inserire il link ai loro articoli, ma li trovi in Rubriche/La Mate-Fisica di Papalla
Grazie Enzo per avere messo insieme i vari articoli sul tema. Ora stampo anche questo e metto insieme agli altri. Sta venendo fuori davvero una bella raccolta Tra l'altro, proprio in questi giorni mia figlia grande (quinto anno liceo scientifico) è alle prese con la massa relativistica , essendo riuscita la sua Prof di Fisica ad arrivare alla RR con il programma (non è da tutti..)
Tra l'altro, proprio in questi giorni mia figlia grande (quinto anno liceo scientifico) è alle prese con la massa relativistica , essendo riuscita la sua Prof di Fisica ad arrivare alla RR con il programma (non è da tutti..)
Incidentalmente: certo che ogni tanto, per argomenti diversi, spunta fuori Richard Feynman con le sue dimostrazioni facili di cose difficili. Ho trovato in rete anche quella della forma ellittica dell'orbita dei pianeti attorno alla propria stella, esposta in una lezione al California Institute of Technology nel 1954. Davvero una mente brillante.
ops.. l'anno era il 1964, non 54.
grazie Arturo,
eh sì, Richard era proprio un genio in tutti i campi. Forse andrebbe studiato a scuola!
Eccellente
Saluti a tutti , questo è il mio primo post. Ho già contattato privatamente Vincenzo , che mi ha dato appuntamento sul blog, e allora eccomi qui, a postare un commento su un argomento che ritengo importante.
Il commento è questo. Fin dagli anni '80 del secolo scorso (o giù di lí...) molti fisici hanno abbandonato l'idea di "massa relativistica" , che aumenta con la velocità secondo la relazione:
dove)  è il solito fattore di Lorentz , ed
 è il solito fattore di Lorentz , ed 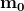  è la cosiddetta " massa di riposo" della particella ( o corpo materiale) , che è in quiete rispetto ad un dato osservatore inerziale ( meglio : in un certo riferimento inerziale, perché come ha fatto notare Vincenzo in un altro scritto si potrebbe essere tentati di pensare ad un OI come ad una persona seduta nell'origine del suo riferimento, che "guarda gli eventi", magari con un binocolo: non è questo il senso di OI ! ) .
 è la cosiddetta " massa di riposo" della particella ( o corpo materiale) , che è in quiete rispetto ad un dato osservatore inerziale ( meglio : in un certo riferimento inerziale, perché come ha fatto notare Vincenzo in un altro scritto si potrebbe essere tentati di pensare ad un OI come ad una persona seduta nell'origine del suo riferimento, che "guarda gli eventi", magari con un binocolo: non è questo il senso di OI ! ) .
Oggigiorno, si stima che circa il 60% dei fisici sia propenso a considerare la massa m come un invariante , né più né meno che uno dei tanti invarianti relativistici .
Perciò , non c'è bisogno di distinguere tra "massa di riposo" e "massa relativistica" , è sufficiente parlare di “massa” di una particella , e considerarla invariante, senza tanti fronzoli .
Lo stesso Einstein , che inizialmente aveva parlato di "massa longitudinale e massa trasversale ", poi cambiò idea , e in una lettera del 1948 al suo amico Barnett scrisse questo :
"It is not good to introduce the concept of the mass M =  of a moving body for which no clear definition can be given. It is better to introduce no other mass concept than the 'rest mass' m. Instead of introducing M it is better to mention the expression for the momentum and energy of a body in motion."
Uno di più combattivi sostenitori del concetto di massa invariante è stato il fisico L.B.Okun , che in un articolo del 2006 dal titolo : THE VIRUS OF RELATIVISTIC MASS IN THE YEAR OF PHYSICS
[questo è il link all’articolo : http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.555.7832&rep=rep1&type=pdf ]
se la prese con i maggiori scienziati che avevano fatto divulgazione , come Hawking e Penrose, per aver scritto che "Einstein aveva scoperto la famosa formula E = mc^2 " , punto e basta , senza ulteriori precisazioni, come se questa formula valesse a tutte le velocità .
La vera scoperta di Einstein , come lo stesso Okun spiega, riguarda l'energia di riposo della particella : 
non quella totale, e per m si deve intendere la massa invariante . E ce ne sono molti altri, di articoli simili, sul web. Per esempio questo : http://arxiv.org/abs/physics/0504110
in cui l'autore fa una disamina di articoli e libri di testo molto diffusi . Del resto, negli anni '60 anche Richard Feynman nelle sue "Lectures on physics" considera la massa relativistica , come ha citato pure Vincenzo. In quegli anni , il concetto di massa relativistica era accettato da (quasi) tutti i fisici . Ma oggi non più .
Ma pensiamoci : che senso ha dire che un elettrone ha una massa a riposo di 0.511 MeV/c^2 , e in moto ad alta velocità ha una massa relativistica&space;=&space;\gamma&space;(v)m_0) , che può raggiungere valori molto grandi se per esempio si porta la velocità a
, che può raggiungere valori molto grandi se per esempio si porta la velocità a 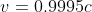 ( qui il fattore di Lorentz vale circa 31.6) ? Lasciamo la massa dell'elettrone al suo valore invariante , e lavoriamo sul fattore
( qui il fattore di Lorentz vale circa 31.6) ? Lasciamo la massa dell'elettrone al suo valore invariante , e lavoriamo sul fattore 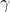 (v) quando necessario . Non è una complicazione , e i risultati finali sono sempre gli stessi.
(v) quando necessario . Non è una complicazione , e i risultati finali sono sempre gli stessi.
Bene, allora se vogliamo riferirci alla massa invariante dobbiamo scrivere la quantità di moto relativistica e l'energia relativistica in maniera diversa .
La qdm sarà data da : 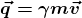 ( nb : questo è un vettore spaziale tridimensionale , che differisce da quello classico per la presenza di
( nb : questo è un vettore spaziale tridimensionale , che differisce da quello classico per la presenza di 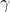 )
)
L'energia relativistica da :
dove K per basse velocità è assimilabile all'energia cinetica classica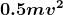 , come noto . Ma per alte velocità ci sono termini aggiuntivi nello sviluppo in serie di
, come noto . Ma per alte velocità ci sono termini aggiuntivi nello sviluppo in serie di 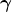 , come noto.
, come noto.
Per ora mi fermo qui, aspetto qualche commento. Poi vorrei parlarvi del 4-vettore energia-impulso, la cui norma invariante è uguale a mc , cioè proprio alla massa invariante della particella , a meno del fattore c .
Resta comunque molto bella e completa la trattazione fatta da Vincenzo.
Caro Pippo,
tra le bozze che non ho mai pubblicato ce n'era proprio uno che riguardava questa visione "moderna" della massa. Poi, però, ho deciso di continuare lungo la strada vecchia. In fondo, si dice comunque la stessa cosa, ma con linguaggio diverso... Personalmente, ritengo decisamente più intuitivo dare il fattore gamma alla massa piuttosto che lasciarlo libero nella quantità di moto. Anche la relazione massa-energia diventa più masticabile. Il fotone ha quantità di moto e già questo sarebbe un concetto assurdo. Donargli una massa perché raggiunge una certa velocità è un concetto che fisicamente non mi spaventa. Personalmente preferisco che gamma sia ingoiato dalla massa, piuttosto che lasciarlo come un fattore indipendente. Per me, comunque, tutto si riduce a una convenzione, ma non lede il concetto più profondo. Tra parentesi, penso di avere evidenziato abbastanza bene che è l'energia a riposo la vera grande conquista...
Del quadrivettore energia-impulso abbiamo parlato abbastanza alla fine dell'articolo... e abbiamo evidenziato bene che è la massa a riposo e/o l'energia riposo che lo costruisce.
E02 = E2 - q2c2
dove E0 = m0 per c=1
Sai, qui, facciamo divulgazione e non possiamo entrare troppo nei dettagli... ma aspettiamo i tuoi commenti con vero piacere!
Salve a tutti è il mio primo intervento. L’incremento d’inerzia relativistico del corpo può considerarsi dovuto al lavoro di compressione per la sua contrazione?
Ad esempio se considero un recipiente di forma cubica di lati L=1, fermo, con all’interno del gas. Se indico con m*vi la quantità di moto di una generica particella i, lungo l’asse X, la forza F che la particella esercita sulla parete ortogonale all’asse X è data dalla variazione della quantità di moto dP = 2*m*vi (si ipotizza l’urto elastico) fra due urti consecutivi nell’unità di tempo dt ossia: F = dP/dt. Indicato con Δt = 2*L/vi il tempo fra due urti consecutivi sulla parete, la forza è:
Fx = dP/Δt = 2m*vi/(2L/vi) = m*vi²/L (1)
Supponiamo adesso che il recipiente si metta in moto lungo x con velocità relativistica v, per la R.R. lo spazio lungo x subisce la contrazione (posto c=1) L’x = L*γ con γ = (1-v²)½ .
La (1) diventa: F‘x = m*vi²/(L*k) = Fx/γ (1a)
Se si moltiplica la (1a) per L si ricava la variazione dell’energia in funzione della velocità v, ossia della contrazione k : E’ = F’x*L= m*vi²/γ = E/γ (1b).
Osservando la (1b) si può dedurre che sia la contrazioni a far aumentare l’energia relativistica E, e che la massa m rimanga costante?
In altre parole, si può ritenere che la contrazione del corpo con la velocità comporti un lavoro di volume (aumento di energia interna per i gas) L = - p*ΔV (in cui Δ = γ)? e che la massa rimanga costante?
ma... hai tenuto conto del diverso tempo tra le collisioni?
Non ho tenuto conto del diverso tempo tra le collisioni.
Se considero il sistema di riferimento solidale con la scatola, oltre a cambiare la scala delle lunghezze, dovrei cambiare anche la scala dei tempi, ossia dilatare il tempo Δt di 1/γ?
Se ciò fosse corretto non ci sarebbe alcun aumento di energia con la contrazione del corpo. Rimane allora la mia domanda: Dove, e sotto quale forma, si accumula l'energia relativistica?
Non capisco bene cosa intendi con "accumula"...
Come si dice nel testo: "L’energia totale di un corpo è data dalla somma di due termini. Il primo è l’energia del corpo quando è in quiete, il secondo è la sua energia cinetica. In altre parole, anche se il corpo resta fermo (K = 0), esso possiede comunque un’energia che dipende soltanto dalla sua massa a riposo (moltiplicata per una costante). Non confondiamola con l'energia potenziale gravitazionale, mi raccomando! Non abbiamo nessun campo gravitazionale...
Ripetiamo ancora un risultato fondamentale per tutta la fisica: Un corpo in quiete possiede una certa energia a riposo (E0) e questa è data proprio dalla sua massa a riposo (a meno di una costante moltiplicativa).
Non riesco a seguire il tuo approccio... e voglio ricordare che qualsiasi fenomeno fisico deve restare lo stesso in tutti i sistemi di riferimento. L'energia a riposo è, inoltre, un invariante.
Buongiorno Enzo
riprendendo l'esempio del simpatico fotone e della sua massa a riposo = 0 ... mi chiedevo se è corretto dire che, dal punto di vista fisico, il fotone è dotato di massa (rigorosamente relativistica) e che tale massa, richiamando la formula dell'effetto fotoelettrico, è = hν/c2
Grazie
Michele
Il fotone, caro Michele, non ha massa, ma quantità di moto. Il tutto è stato spiegato anche nei commenti. Parlare di massa relativistica è un concetto che a molti non piace (e probabilmente a ragione), ma rende più semplice la trattazione in termini divulgativi e il succo finale non cambia.
Ciao a tutti, primo intervento e scusate se ci vado subito giù pesante:
Einstein non ha spiegato a Lorentz che la sua trasformazione matematica è un'estensione analitica di un problema fisico... e da quel giorno le cose sono degenerate... troppo...
Quello che mi pare che Einstein abbia scoperto è questo:
Wmax= (v+u)max = C
Cioè non si può far superare, ad una massa, la velocità della luce. Se metti un razzo su un carrello, sopra ad un altro carrello appoggiato sui binari, che viaggia già a velocità v, per tanto potenti siano i suoi motori, la velocità W che può raggiungere rispetto al sistema di riferimento fisso (se u è quella relativamente al carello appoggiato sui binari) è Wmax =c da cui Wmax=(u+v)=c.
E non può andare oltre non per le trasformazioni di Lorentz !, ma per quanto enunciato da Einstein: non c'è modo di accelerare la massa oltre la velocità (media) della luce. (per un problema di impossibilità di eiettare mazze oltre la velocità della luce, quindi mancanza di vincoli su cui spingere, cioè di possibile differenza di velocità... per dirla in soldoni).
Quindi sarebbe da chiarire che il trucchetto con cui si spiega che se u+v=2c lascia inalterata la velocità somma = c è puramente dovuto alle proprietà dell'estensione analitica utilizzata per comodo, ma non è realistica. Fortunatamente l'estensione analitica (cioè la trasformazione di Lorentz) funziona correttamente anche mettendo u=(c-v) perchè a limite per v (o u) =c nulla cambia visto che la complementare si azzera e il rapporto resta c/c =1.
Sarebbe questione di buona fisica, a se ancora oggi non lo leggi su libri (considerati testi sacri) che dovrebbero avere un certo peso c'è da preoccuparsi... non credete ?
Scusate, ma sto leggendo proprio in questi giorni Susskind "Relatività ristretta e teoria classica dei campi. Il minimo indispensabile per fare della (buona) fisica"
...e mi si è accaponata la pelle...
Se fosse vero quanto enunciato da Lorenz saremmo spacciati. Dato che Einstein ha scoperto solo quel che accade fino a c (e non è riuscito ad andare oltre), siamo ben lieti di dover studiare con tutte le nostre energie come andare oltre, cioè come sarà possibile mettere in salvo il genere umano, quando sarà necessario abbandonare il ns. sistema solare...
caro Stefano,
non sono riuscito a capire bene tutte le tue congetture... ma guarda che la velocità della luce è quello che è e non dipende da Einstein, ma Einstein ne prende atto e, facendo, questo ricava la relatività. Che poi nessuna massa riesca a raggiungerla è un dato di fatto che conferma il dato di partenza.
"Sarebbe questione di buona fisica, a se ancora oggi non lo leggi su libri (considerati testi sacri) che dovrebbero avere un certo peso c'è da preoccuparsi... non credete ?" Questo tipo di frasi che mettono in dubbio decenni di studi profondi e continuamente confermati, non riesco a sopportarli su questo blog...
"Se fosse vero quanto enunciato da Lorenz saremmo spacciati. Dato che Einstein ha scoperto solo quel che accade fino a c (e non è riuscito ad andare oltre), siamo ben lieti di dover studiare con tutte le nostre energie come andare oltre, cioè come sarà possibile mettere in salvo il genere umano, quando sarà necessario abbandonare il ns. sistema solare..."
Cosa avrebbe enunciato Lorentz che dovrebbe spaventarci? Non riesco a capirlo...
In ogni modo, io, una pulce rispetto ad Einstein, non riesco ad andare oltre. Se tu ci riesci, fai pure e mandaci il lavoro finale, avallato da una pubblicazione scientifica con referee...
Ti prego... non siamo un forum in cui si può dire quello che si vuole...