Categorie: Meccanica quantistica
Tags: diffrazione effetto Compton effetto fotoelettrico effetto tunnel elettroni energia fotoni Principio di eclusione di Pauli principio di Heisenberg quantità di moto scattering
Scritto da: Vincenzo Zappalà
Commenti:24
Effetti e principi della Meccanica Quantistica ***
Questo articolo è stato inserito nella pagina d'archivio dedicata alla Meccanica Quantistica, nella quale troverete articoli che, pur rimanendo sempre ad un livello semplice e divulgativo, trattano l'argomento a livelli diversi di difficoltà, a partire da quelli adatti anche ai bambini.
Abbiamo già riassunto a grandi linee la meccanica quantistica, utilizzando principalmente quel capolavoro che è l'esperimento della doppia fenditura di Feynman (QUI). Lo stesso genio ci ha permesso di descrivere l'elettrodinamica quantistica, la QED, dove si analizzano e si spiano i comportamenti di due attori fondamentali del teatro del Cosmo: l'elettrone e il fotone. La meccanica quantistica (MQ) non si esaurisce certo così in fretta ed essa penetra all'interno dell'atomo e dà luogo a effetti e principi che sembrano regolare in modo molto illogico, ma perfettamente descrivibile, "quasi" tutta la Natura.
In questo articol...one mettiamo insieme quelli più importanti e spiegabili senza un uso eccessivo di formule. Tra essi quello che io giudico la base stessa del TUTTO (il principio di Heisenberg) e la sua "quasi" ovvia conseguenza che permette alla materia di esistere (il principio di esclusione di Pauli). Non possiamo certo dimenticare l'effetto tunnel che permette alle stelle di vivere e di produrre l'energia atta a controbilanciare la gravità, ma un posto di rilievo dobbiamo darlo all'effetto che ha dato il vero e proprio via a tutta la MQ (l'effetto fotoelettrico) e a quello non meno importante che è l'effetto Compton. L'idea di base, dovuta a Planck, è stata, invece, descritta nella storia dell'atomo e nella spettroscopia stellare (catastrofe ultravioletta e conseguenze varie).
Insomma, un bel ripasso e uno stimolo a conoscere sempre meglio l'affascinante microcosmo e le sue leggi degne di Alice nel Paese delle Meraviglie. Sempre aspettando che la Scuola capisca che è giunto il momento di introdurre la meccanica quantistica fin dalle medie...
La prova decisiva fornita da chi non c'ha mai creduto: l' EFFETTO FOTOLELETTRICO
L’effetto fotoelettrico, spiegato da Einstein, è di una semplicità irrisoria. Come tutte le rivoluzioni più grandi della storia della mente umana non può che apparire semplice, pur nascondendo una cambiamento drastico nella visione della realtà. Mi permetto di fare ricorso a uno dei miei soliti paragoni “artistici”, sperando di non annoiarvi (ma Arte e Scienza sono solo due facce di una stessa medaglia culturale). Il titolo poteva, quindi, anche essere: “La Flagellazione di Urbino”, del sommo Piero della Francesca. Proprio per questo ho inserito il capolavoro assoluto nell’immagine che segue…
E’ difficile dire chi ha veramente dato il via alla meccanica quantistica. Da un punto di vista teorico si pensa subito a Planck che con i suoi pacchetti d’energia aveva spiegato “matematicamente” l’andamento della curva di corpo nero, risolvendo il problema della catastrofe ultravioletta (per saperne di più, rimando alla serie di articoli sulla storia dell’atomo). Tuttavia, come già detto varie volte, Planck, per primo, non pensava minimamente che questa soluzione “di comodo” potesse essere veramente un effetto reale. Dal punto di vista “pratico”, proprio colui che poi osteggiò duramente la meccanica quantistica a causa della rottura che causava nella visione deterministica dei processi naturali, ossia Einstein, risolse con poche frasi l’effetto fotoelettrico, prova definitiva della concreta realtà della teoria di Planck.
L’effetto fotoelettrico spiegato da Einstein è estremamente semplice, per cui vorrei darne una visione più artistica che fisica, proprio per far capire la rivoluzione che ha innescato quasi nell'anonimato. Un qualcosa di molto simile al passaggio dall’arte gotica, perfetta, cesellata, elegantissima e quella rinascimentale, solida, concreta, essenziale.
L’effetto fotoelettrico era stato individuato già nel 1887 da Hertz e successivamente analizzato da altri colleghi. Le conclusioni dei vari esperimenti, sebbene entusiasmanti e ben descrivibili, rimanevano senza una spiegazione plausibile. Richiamiamone brevemente alcune, inserendo qualche commento, senza farne una vera storia (meriterebbe un piccolo romanzo):
1) dischi di metallo caricati negativamente perdono la loro carica se investiti da luce ultravioletta.
Ciò è dovuto a un arrivo di cariche positive che annullano quelle negative o da cariche negative che abbandonano il disco? Gli elettroni, appena scoperti, danno ragione alla seconda ipotesi. Sta iniziando l’era dello studio delle interazioni tra radiazione luminosa e materia, che Feynman ha reso un’avventura fantastica con la sua QED.
2) gli elettroni che lasciano il catodo variano la propria velocità in funzione della frequenza della luce utilizzata, ma in modo indipendente dalla sua intensità. Ovviamente, aumentando l’intensità luminosa aumenta il numero di elettroni prodotti, ma non varia assolutamente la loro energia.
In poche parole, questo vuol dire che se aumentiamo la luminosità, produciamo un numero maggiore di elettroni, ma ognuno di loro mantiene la stessa energia (o -se preferiamo- velocità, dato che energia cinetica e velocità sono strettamente collegate). Per “vivacizzare” veramente gli elettroni bisogna cambiare la frequenza. Più è alta e meglio è.
Tutto molto bello e inaspettato, ma qual è la ragione di questo comportamento? Innanzitutto, qual è il vero colpevole del fenomeno? Il materiale di cui sono fatti i “dischi” o proprio la luce che li investe? Ricordiamo che, con grande fatica, si è appena risolto il problema della sua natura ondulatoria. E se la luce è un’onda ci si aspetterebbe che più l’onda è ampia e più riesce a smuovere qualcosa che gli si para d’avanti. Pensate a un maremoto… fa più danni una serie di poche onde di enorme altezza o una serie di moltissime onde di ampiezza irrisoria? Penso che chiunque propenderebbe per la prima soluzione.
Lenard, ad esempio, proprio sulla base del ragionamento apparentemente più logico, pensava che la “colpa” di tutto risedesse nella struttura degli atomi colpiti. Thompson, invece, propendeva per la luce, ma si arenava, comunque, dato che, bene o male, l’intensità della luce non poteva essere trascurabile. E, invece, bastava superare una soglia di frequenza e anche una radiazione di bassissima intensità smuoveva immediatamente gli elettroni. Piccole onde, a ritmo forsennato, producevano più energia di poche onde mostruose.
Se gli scienziati di quei tempi avessero letto l’esempio che abbiamo fatto noi, per spiegare la catastrofe ultravioletta (quello dei tanti piccoli secchi molto più utili dei pochi secchi enormi, per svuotare un pozzo pieno d’acqua… ricordate?), non avrebbero avuto difficoltà a risolvere l’enigma. Purtroppo non l’hanno fatto e sono rimasti in grave crisi (sto scherzando, ovviamente!).
Tutti tranne uno, però! Indovinate chi? Lui, sempre lui, Albert! Capace, ancora una volta, di non soffermarsi sull’esperimento in sé, ma di inquadrarlo in un contesto ben più ampio. Pensate che gli sono bastate tre paginette per spiegare l’effetto fotoelettrico, considerandolo solo un esempio di un ragionamento ben più generale e articolato. Siamo nel 1905, tanto per chiarirci le idee.
Einstein sta analizzando i fenomeni collegati alla radiazione del corpo nero e non è insensibile a quella strana soluzione matematica proposta da Planck. Ma, ancora più importante per lui, è l'asimmetria che nota negli studi di fisica classica relativi all’elettromagnetismo. Una questione di eleganze e di estetica, in fondo… E’ possibile che la materia si comporti in modo discontinuo, mentre la radiazione elettromagnetica presenti una natura “continua”? Avesse potuto parlare con Feynman e discutere di QED…
Einstein, in poche parole, cerca di rendere “reale” la strada “artificiosa” dei quanti di Planck, nati come puro calcolo solo cinque anni prima. In qualche modo, più che un grande fisico, Einstein assomiglia a un grande pittore che si accorge che, malgrado la grande tecnica pittorica mostrata, il quadro che ammira ha qualcosa di disarmonico che disturba l’insieme.
Permettetemi uno dei miei soliti voli verso il Rinascimento… Le nuove composizioni create da Maestri come Masaccio o Piero della Francesca (tanto per citarne due tra i tanti) non si fermano alla pura rappresentazione, ma sono opere di intensa preparazione geometrica e matematica. Seguendo gli antichi canoni della bellezza greca, pensano che sia fondamentale, prima di stendere il colore e dare forma ai personaggi, che si prepari lo spazio in cui farli vivere con i piedi ben ancorati per terra. Solo così, l’equilibrio tra i pieni e i vuoti, le traiettorie delle direzioni preferenziali, ecc., ecc., riescono a creare un insieme armonico e appagante.
Per chi avesse voglia di approfondire, consiglio di guardare con attenzione un capolavoro assoluto come la Flagellazione di Urbino, di Piero della Francesca. Esso, prima che un dipinto, è la soluzione di un teorema matematico e geometrico apparentemente irrisolvibile. Metà del quadro è composto di “pieno”, tre figure che sembrano creare una struttura massiccia in rotazione. L’altra metà è di puro vuoto, uno spazio senza peso. Eppure le due parti sono perfettamente bilanciate tra di loro e danno un senso di perfetto equilibrio. La prospettiva, la sua applicazione, la scelta delle dimensioni e dei rapporti, hanno creato il miracolo. In parole povere, non vi è differenza tra la materia e l’apparente vuoto. Un concetto che tanto assomiglia ai nuovi principi della fisica che sta nascendo agli inizi del 1900…
Scusate la digressione e torniamo alla nostra luce e alla sua interazione con gli elettroni degli atomi del metallo colpito. All’Einstein artista della fisica non resta che eliminare l’apparente discontinuità tra luce e materia e pensare la prima come portatrice di energia secondo “pacchetti” collegati alla frequenza dell’oscillazione dell’onda. Insomma, rendere concrete le ipotesi di Planck.
Einstein rimette in discussione la teoria di Maxwell, che considera, comunque, una svolta geniale e decisiva, dato che è proprio lei che gli fornirà il punto di partenza per la relatività. In particolare, si accorge che essa è sicuramente valida per i fenomeni macroscopici, ma niente assicura che si possa applicare anche a quelli microscopici (una visione puramente e straordinariamente quantistica). Per loro devono esistere principi differenti, legati proprio ai “quanti” appena nati.
Sebbene la teoria ondulatoria della luce spieghi quasi tutti i fenomeni macroscopici, Albert ritiene che essa possa “non essere adeguata”, quando è applicata a fenomeni di emissione e trasformazione della luce, di cui l'effetto fotoelettrico è solo un esempio. Nasce quindi l’ipotesi che anche l'energia sia distribuita nello spazio in modo discontinuo (sparisce l'asimmetria che tanto lo irritava). Basta allora riferirsi all'ipotesi di Planck: la luce non deve essere più considerata un qualcosa di continuo ma deve essere costituita da "quanti di luce" o fotoni. E’ nata una particella non-particella fondamentale per la fisica futura, anche se il nome gli sarà dato circa vent’anni dopo.
Riportiamo una frase di pugno dello stesso Albert: "Secondo l'ipotesi che voglio qui proporre, quando un raggio di luce si espande partendo da un punto, l'energia non si distribuisce su volumi sempre più grandi, bensì rimane costituita da un numero finito di quanti di energia localizzati nello spazio, che si muovono senza suddividersi e che non possono essere assorbiti o emessi parzialmente."
Come vedete, niente di veramente indirizzato solo verso la spiegazione di un effetto fisico particolare, ma qualcosa di estremamente generale. Una nuova visione dell’arte… ops… della fisica!
Basta utilizzare la semplice e fondamentale relazione:
E = hν
dove E è l’energia di un singolo “quanto”, h è la costante di Planck e ν la frequenza. Insomma. I famosi secchielli per raccogliere l’acqua del pozzo (vedi articoli sulla spettroscopia).
A questo punto, diventa veramente banale l’equazione che descrive l’effetto fotoelettrico. Un elettrone colpito da un quanto acquisterà un’energia cinetica K, data da:
K = hν – w
Dove w è il lavoro che deve essere svolto per “sradicare” l’elettrone dal suo atomo. w dipende, quindi, dal tipo di atomo di cui è composto il materiale illuminato. K è ovviamente data da:
K = 1/2 meve2
Dove me e ve sono massa e velocità dell’elettrone.
Vale nuovamente la pena citare la frase esplicativa dello stesso Einstein: “La consueta concezione, per la quale l'energia della luce si distribuisce in modo continuo nello spazio irradiato, incontra, nel tentativo di spiegare i fenomeni fotoelettrici, notevoli difficoltà, che sono state fatte oggetto di uno studio particolarmente approfondito dal Signor Lenard. Partendo dal principio che la luce eccitatrice è costituita di quanti di energia hν, l'emissione di elettroni si può spiegare nel seguente modo. I quanti di energia penetrano nello strato superficiale del corpo e la loro energia si trasforma, almeno in parte, in energia cinetica di elettroni... Inoltre va supposto che ogni elettrone, nell'abbandonare il corpo, debba effettuare un lavoro w (che è caratteristico del corpo considerato). Ad uscire dal corpo con la massima velocità normale saranno gli elettroni eccitati che si trovano direttamente alla sua superficie e che acquistano una velocità normale ad essa".
Più chiaro e semplice di così… Chiedete a Piero della Francesca come ha fatto a creare un capolavoro quasi impossibile da concepire e vi dirà che è bastato fare "uno più uno uguale a due" (o poco di più).
Una piccola nota aggiuntiva, non certo trascurabile. Ricordiamo che Planck aveva ipotizzato che solo gli scambi di energia fossero quantizzati, ma non la radiazione stessa. Einstein non ha, quindi, fatto solo un “copia e incolla”!
Per concludere, fatemi ricordare i miei primi anni osservativi in cui non erano rare le notti invernali (spesso consecutive) di dieci ore passate al freddo della cupola per studiare le variazioni luminose degli asteroidi. L’apparecchiatura che era inserita al telescopio (un 45 cm, poco più che amatoriale al giorno d’oggi) ci permetteva di contare i “fotoni” provenienti dal piccolo pianeta e dalle stelle di confronto e, tra l’altro, di aprire la strada a una nuova visione degli asteroidi, quella fisica e non più puramente dinamica.
Noi li chiamavamo “fotoni” e li vedevamo scorrere uno a uno, anche se in realtà si contavano gli elettroni che venivano “staccati” dai pacchetti di energia luminosa. Usavamo un fotometro fotoelettrico e quante volte ho pensato al genio di Einstein… E quante volte, durante il conteggio, ho guardato il cielo che appariva vuoto (a parte le stelle e i pianeti) e ho pensato a tutto quell’andare e venire di informazioni che lo attraversavano continuamente e a tutti i campi che lo riempivano in ogni angolo più nascosto.
No, anche senza oculari costosissimi e senza cercare galassie praticamente invisibili, non ho mai pensato che il Cosmo potesse essere qualcosa di veramente vuoto.
Un biliardo microscopico: l'EFFETTO COMPTON
La QED ci ha mostrato come l'interazione tra materia ed energia elettromagnetica si possa risolvere con poche lettere di un alfabeto quantistico. Già l'effetto fotoelettrico ci ha mostrato che possono esistere (al di là della visione ondulatoria della luce) veri e propri urti tra fotoni ed elettroni. Ogni interazione di questo tipo ha un nome molto semplice nella QED: scattering. Ne descriveremo, adesso, uno altrettanto importante per la fisica, che ci ricollega alla meccanica classica. Più esattamente al gioco del biliardo... Ancora una volta, impareremo che per parlare di fisica moderna è fondamentale avere le idee chiare su quanto ci ha insegnato e ci insegna la fisica classica. Mi dilungherò, perciò, abbastanza sui preamboli per passare, poi, alla parte essenzialmente quantistica. Molti concetti li conoscete, ormai, molto bene, ma penso che non faccia mai male ripeterli... Al limite, prendeteli solo come un "ripasso" forzato.
Urto centrale
Io giocavo soprattutto a “boccette” e a biliardo non ero molto bravo. Tuttavia, ne sono sempre stato affascinato, sia per la bellezza delle traiettorie che si dovevano immaginare prima di tirare il colpo, sia per le implicazioni continue dei principi di meccanica classica. Sto parlando, ovviamente, di un tavolo da biliardo perfetto e non come quelli in cui io andavo da liceale a fare le partite (pagava chi perdeva, niente di più…). Perfetto vuole dire che le sponde rispondono perfettamente e che il piano è ultra liscio, annullando quasi del tutto gli attriti. Anche le sfere da gioco devono essere lavorate perfettamente e ben calibrate.
Con un biliardo e qualche tiro banale (sena nemmeno calcolare le sponde, ma solo gli urti iniziali) c’è già da scrivere un manuale di meccanica classica. Con poche “noiose” formulette si riesce già ad avere una riprova pratica eccezionale. Per arrivare nientemeno che a un biliardo quantistico, con palle da gioco molto particolari, è necessario partire dall’inizio e affrontare il problema a una dimensione e passare poi a quello bidimensionale (vedremo esattamente cos’è).
Dobbiamo, però, introdurre alcune grandezze della fisica, sulle quali, però, siamo già andati spesso a curiosare. Ripetere, tuttavia, non fa mai male e quindi un bel ripasso non ve lo leva nessuno...
Tutti sappiamo cosa sono la massa (inerziale in questo caso) e la velocità di un corpo. Con loro possiamo fare molte cose. Innanzitutto, definire la quantità di moto. Come ben sapete, essa è una grandezza fisica che mi è particolarmente simpatica e nel libro "La Fisica Addormentata nel Bosco" la paragono a una lumaca che si porta sempre dietro la sua “casetta”. La casetta non è altro che la massa, un peso che limita o -meglio- regola la capacità di movimento, ma che, contemporaneamente, dà una certa sicurezza e resistenza. La quantità di moto si definisce come il prodotto della velocità v1 di un corpo moltiplicata per la sua massa m1. Scriviamola:
q1 = m1v1 …. (1)
Essa è quella che è e poco importa se sia stata causata da una forza o da qualsiasi altra cosa. L’importante è che rappresenti una proprietà di un corpo con una certa massa che si muove con velocità costante. Essa definisce, in qualche modo, proprio la capacità del corpo, di una certa massa, di mantenere un moto a velocità costante.
Se la massa cresce, a parità di velocità che si vuole ottenere, deve aumentare la capacità di muoversi dell’oggetto, ossia proprio la quantità di moto. Se scriviamo la (1) come v1 = q1/m1, capiamo molto bene cosa comporta una massa più grande. A parità di quantità di moto, la velocità è costretta a diminuire. La massa è quindi quel qualcosa che cerca di opporsi al moto, proprio un’inerzia che il corpo si porta dietro (da cui massa inerziale).
Per la sua stessa definizione, la quantità di moto è una grandezza costante per un corpo che si muove a velocità costante. In parole più “fisiche”: un corpo (o un sistema chiuso) conserva la propria quantità di moto, se nessuna forza esterna lo viene a disturbare. Abbiamo così introdotto un concetto fondamentale per la meccanica: la conservazione della quantità di moto.
Non è facile non essere disturbati nell’Universo, ma la quantità di moto cerca di farlo con tutta la sua capacità indiscussa. Possiamo immaginarci la lumachina mentre assume la forma di una palla da biliardo e si muove sul tappeto verde senza alcun attrito (sarebbe una forza esterna!). Essa rappresenta un sistema fisico chiuso e come tale mantiene inalterata la sua quantità di moto, sempre che nessuna forza esterna (attriti o altro) la venga a disturbare. Nel gioco del biliardo, però, questo non è auspicabile, se no che divertimento ci sarebbe a vedere correre una palla bianca su un tavolo infinito? Per quello che ci interessa, trascuriamo, comunque, gli urti contro le sponde e pensiamo solo all’altra palla in gioco (e magari anche al pallino).
Prima di prendere la stecca in mano, però, dobbiamo introdurre un’altra qualità o capacità della nostra sfera in movimento. Essa possiede anche una certa energia, che deriva proprio dal suo movimento e dalla massa. Cos’è l’energia? Non è facile rispondere in termini "terra-terra", ma iniziamo a definirla come la capacità di un corpo di compiere un lavoro (lavoro “fisico” che è un po’ diverso dal nostro lavoro). L’energia che deriva solo da queste grandezze, massa e velocità, prende il nome di energia cinetica.
Volete provarla? Prendetevi in faccia una palla da biliardo e poi vedrete che cosa rappresenta questa energia! Sicuramente, la “botta” terribile che subite dipende dalla massa della sfera, ma ancora di più dalla sua velocità. Se un asteroide di piccole dimensioni fosse appoggiato delicatamente al suolo, farebbe del male solo agli insetti che si trovano sotto di lui. Ma se arrivasse a una velocità di parecchi chilometri al secondo, la situazione sarebbe di gran lunga più catastrofica. Scriviamo allora la formula che definisce l’energia cinetica di un corpo che si muove con una certa velocità v1 e che possiede una certa massa m1:
E1 = ½ m1v12 …. (2)
Non è molto diversa dalla quantità di moto, in fondo, dato che si ottiene moltiplicando q per v e dividendola per due. Tuttavia, rappresenta qualcosa di fisicamente diverso, in qualche modo indipendente. Per trovare una vera relazione dovremmo andare troppo a fondo della questione e non possiamo farlo adesso. Ci basti la definizione che abbiamo dato. Al limite, possiamo notare un’altra somiglianza, non certo casuale (niente di casuale vi è nella meccanica classica e nella relatività), con la celeberrima formula di Einstein: E = mc2. c è proprio una velocità (quella della luce), m la massa ed E l’energia… Che bella è la fisica e com'è intrigante capire tutte le sue connessioni.
Basta così e torniamo al biliardo. Prima di iniziare, però, ricordiamo che anche l’energia si conserva come la quantità di moto, se niente viene a disturbare il corpo. In questo caso, l’unica energia in gioco è quella cinetica (ci sarebbe da parlare anche di quella dovuta alla gravità della Terra, ma a questo ci pensa il tavolo da gioco e non la nominiamo nemmeno).
La nostra sfera si muoverebbe tranquilla conservando le sue due proprietà che abbiamo appena conosciuto. Tuttavia, il gioco del biliardo si basa proprio nel cercare di colpire un’altra sfera, ossia di urtarla. Non possiamo certo illuderci: un urto deve essere considerato a tutti gli effetti un “disturbo” esterno e la nostra palla è costretta a cambiare sia la quantità di moto che l’energia cinetica.
Immaginiamo, in questa prima parte, che l’urto avvenga in modo che il percorso della prima sfera passi esattamente per il centro della seconda sfera (i centri di massa sono perfettamente allineati con la direzione del moto). Se anche la seconda sfera si muove, la direzione del suo moto deve essere uguale a quello della prima. In questa situazione, tutto quello che succede avviene lungo questa direzione, non potendosi originare movimenti laterali (non vi sono momenti di forza e cose del genere…).
Un bel problemino, raffigurato schematicamente nella Fig. 1.

Come faccio a prevedere cosa succede dopo che le due sfere si sono scontrate? Qui bisogna fare un breve discorsetto di logica fisica. Fino al momento del contatto tra le due sfere siamo di fronte a due sistemi chiusi: la palla che rotola e la palla ferma o che rotola in verso opposto (non vi sono altri moti permessi dato che vogliamo che tutto avvenga lungo una sola linea). Della prima sfera sappiamo tutto. Lo stesso vale anche per la seconda, che ha una velocità v2 e una massa m2. Analogamente, anch’essa avrà una quantità di moto q2 e un’energia cinetica E2, date da:
q2 = m2v2
E2 = ½ m2v22
Anche la seconda fa di tutto per conservare le sue due capacità. I corpi naturali, però, non hanno paura dei “diversi” e se incontrano qualcuno pensano subito a come accordarsi per avere un interesse comune o quanto meno una soluzione largamente condivisa. Ecco, la parola base: condivisione. Nel momento del contatto si originano delle forze. Tuttavia. le forze, quelle che causano un cambiamento nelle proprietà delle due sfere, sono una uguale e contraria all’altra (uno dei principi di base della meccanica: ad ogni azione corrisponde una reazione uguale e contraria). La prima sfera subisce quella della seconda, la seconda quella della prima. Se continuiamo a considerare le due sfere separate, ognuna DEVE cambiare la sua quantità di moto e la sua energia cinetica. Ma se le due sfere si mettono d’accordo e nel momento in cui si toccano decidono di considerarsi un corpo solo o -meglio- un unico sistema chiuso? Lo so, lo so, per noi umani è pura utopia, ma non per le sfere o le particelle della Natura.
Accettata questa condizione, cosa succede al nuovo sistema formato dalle due sfere nel momento dell’urto? Le due forze che subiscono le due palle di biliardo si annullano a vicenda (una forza è uguale e contraria all’altra) e il nuovo sistema ampliato NON subisce nessuna forza esterna. Ma se non subisce nessuna forza esterna deve conservare sia la quantità di moto che l’energia cinetica. Ovviamente, per conservarle devono unirle insieme, dato che quelle che si conservano sono le proprietà dell’intero sistema (solo lui non ha subito forze esterne). Si deve avere perciò:
q1 + q2 = costante1
E1 + E2 = costante2
Sì, ma cosa sono queste costanti? Beh… è facile scriverle. Durante l’urto avviene uno scambio di informazioni tra le due sfere e, in base alla loro massa e alla loro velocità precedenti, esse devono condividere e/o scambiarsi le grandezze in gioco. Ovviamente non possono scambiarsi la massa, ma le velocità sì. L’importante è che rimangano costanti la quantità di moto e l’energia cinetica complessive. Questo regalo reciproco decide la loro esistenza dopo che si saranno di nuovo allontanate per vivere nuovamente da “single”. Ovviamente, a quel punto, ognuna possiede una quantità di moto e una energia cinetica diverse da quelle che aveva prima dell’urto, ma sono riuscite a conservare quello totale nell’istante in cui erano attaccate tra loro e formavano un solo sistema.
Ne segue, quindi, che la quantità di moto totale (e l’energia cinetica) deve rimanere inalterata anche dopo l’urto. Ossia, le costanti non sono altro che le somme delle quantità di moto e di energia cinetica calcolate dopo l’urto, ossia:
q1 + q2 = q1’ + q2’
E1 + E2 = E1’ + E2’
Queste due relazioni dicono solo che si è avuta la conservazione della quantità di moto e dell’energia cinetica. Vale la pena accennare al fatto che stiamo parlando di urti elastici. Ossia, tutta l’energia in gioco resta solo energia cinetica. Escludiamo quindi lo schiacciamento “fisico” delle due sfere, la produzione di calore, il rumore dell’urto, ecc., che introdurrebbero altri tipi di energia. Forse, per le palle di biliardo è molto difficile essere in queste condizioni perfette, ma per le particelle del microcosmo quantistico è invece una scelta perfetta.
Se chiamiamo v1’ e v2’ le nuove velocità delle due sfere, la conservazione della quantità di moto e dell’energia cinetica si scrivono :
m1v1 + m2v2 = m1v1’ + m2v2’ conservazione quantità di moto …. (3.1)
½ m1v12 + ½ m2v22= ½ m1v1’2 + ½ m2v2’2 conservazione energia cinetica …. (3.2)
Come capita praticamente in tutti i problemi di meccanica classica, questo tipo di equazioni sono quelle che permettono la soluzione. E’ sempre fondamentale scrivere le relazioni che descrivono la conservazione dell’energia totale e/o di altre proprietà come il momento angolare o la quantità di moto o altro ancora. Ricordatevelo bene, perché la fisica lavora quasi sempre così.
Un’altra osservazione. La trattazione che faremo adesso è la più generale possibile (sempre nel caso di una sola dimensione) e va oltre il gioco del biliardo, nel quale la seconda sfera è sempre ferma e ha la stessa massa della prima (a parte il pallino). Noi invece considereremo anche i casi in cui la seconda sfera è in movimento e ha una massa qualsiasi. I casi da biliardo saranno casi particolari di uno ben più generale. Se dobbiamo fare le cose, facciamole bene!
A questo punto, rassegnatevi! Useremo la matematica che abbiamo iniziato a conoscere per risolvere il problema fisico che è stato riassunto nelle due relazioni (3.1 e 3.2). Che cosa vogliamo trovare, alla fine? Beh… non c’è molta scelta: le velocità delle due sfere dopo l’urto (le masse rimangono quelle che sono). Ce la faremo? Sicuramente sì, perché abbiamo due incognite (v1’ e v2’) e due relazioni che le legano a quelle conosciute. Tiriamoci su le maniche e iniziamo. Come vedrete ho usato solo cose che già dovete sapere, niente di più complicato…
I termini noti sono: v1, v2, m1, m2. Quelli che dobbiamo trovare (in funzione di quelli noti) sono v1’ e v2’.
Ricordiamoci subito un prodotto notevole:
a2 – b2 = (a + b) (a – b)
Lo useremo subito per cercare di semplificare le nostre relazioni di partenza (soprattutto la seconda). Eseguiamo di volta in volta alcune operazioni come “raccogliere”, “mettere in evidenza” e altre cosucce del genere:
m1v1 + m2v2 = m1v1’ + m2v2’
½ m1v12 + ½ m2v22 = ½ m1v1’2 + ½ m2v2’2
m1v1 - m1v1’ = - m2v2 + m2v2’
m1v12 - m1v1’2 = - m2v22 + m2v2’2
m1(v1 - v1’) = - m2(v2 - v2’)
m1(v12 - v1’2) = - m2(v22 - v2’2)
m1(v1 - v1’) = - m2(v2 - v2’)
m1(v1 - v1’) (v1 + v1’) = - m2(v2 - v2’) (v2 + v2’)
A questo punto inserisco la parte destra della prima relazione nella seconda, dato che i termini in grassetto sono uguali:
- m2(v2 - v2’) (v1 + v1’) = - m2(v2 - v2’) (v2 + v2’)
Semplifico le parti in comune a sinistra e a destra:
(v1 + v1’) = (v2 + v2’)
Da cui:
v2’ = v1 + v1’ - v2 …. (4)
Adesso, torno alla prima relazione (quella della quantità di moto):
m1(v1 - v1’) = - m2(v2 - v2’)
e sostituisco il valore di v2’ con quello che ho appena ottenuto:
m1(v1 - v1’) = - m2(v2 - v1 - v1’ + v2) = - m2(2v2 - v1 - v1’)
m1v1 - m1 v1’ = - 2m2v2 + m2v1 + m2 v1’
m1v1 - m2v1 + 2m2v2 = m1 v1’ + m2 v1’
v1(m1 - m2) + 2m2v2 = v1’(m1 + m2)
v1’ = v1(m1 - m2)/(m1 + m2) + 2 m2v2/(m1 + m2) …. (5)
Abbiamo ottenuto la velocità della prima sfera dopo l’urto, in funzione di quantità ben conosciute.
Passiamo adesso a v’2, riprendendo in mano la (4)
v2’ = v1 + v1’ - v2
Non ci resta che sostituire al posto di v1’ il valore (5) appena trovato (che barba!):
v2’ = v1 + v1(m1 - m2)/(m1 + m2) + 2 m2v2/(m1 + m2) - v2 =
= (v1 m1 + v1 m2 + m1v1 - m2v1)/(m1 + m2) + (2 m2v2 - v2m1 - v2m2)/(m1 + m2) =
= 2v1 m1/(m1 + m2) + (m2v2 - v2m1)/(m1 + m2)
v2’ = v2(m2 – m1)/(m1 + m2) + 2v1 m1/(m1 + m2) …. (6)
La (5) e la (6) risolvono il nostro problema. Imponendo la conservazione della quantità di moto e dell’energia cinetica totali, siamo riusciti a determinare le nuove velocità delle due palle da biliardo, nel caso monodimensionale più generale possibile. Divertitevi pure a fare casi particolari fin che volete. Ovviamente, se le due palle vanno in verso opposto tra loro, dovete cambiare il segno alla seconda velocità…
Facciamo, adesso, dei casi particolari, che sono proprio quelli più interessanti per il biliardo.
(a) m1 = m2
Le due masse sono uguali, ma le velocità sono qualsiasi.
La (5) e la (6) dicevano:
v1’ = v1(m1 - m2)/(m1 + m2) + 2 m2v2/(m1 + m2)
v2’ = v2(m2 – m1)/(m1 + m2) + 2v1 m1/(m1 + m2)
Basta imporre m1 = m2 ed esse diventano
v1’ = 2 m2v2/2 m2 = v2
v2’ = 2 m1v1/2 m1 = v1
Le velocità si scambiano tra loro
(b) m1 = m2, v2 = 0
Le due masse sono uguali e, inoltre, la seconda sfera è ferma (caso tipico del biliardo nel tiro iniziale)
v1’ = v2 = 0
v2’ = v1
La prima si ferma e la seconda parte con la velocità della prima
(c) m1 >> m2, v2 = 0
La seconda palla è ferma, ma la massa della prima è molto più grande della seconda (caso del pallino… più o meno). Cominciamo col mettere v2 = 0.
v1’ = v1(m1 - m2)/(m1 + m2)
v2’ = 2v1 m1/(m1 + m2)
Poi assumiamo che m1 >> m2 ossia:
m1 +/- m2 ~ m1
da cui:
v1’ ~ v1
v2’ ~ 2v1
La prima continua, quasi, con la stessa velocità, mentre la seconda parte a velocità quasi doppia della prima
(d) m1 << m2, v2 = 0
Manteniamo, sempre, la seconda sfera ferma, ma consideriamo quest’ultima molto più massiccia della prima. Poniamo come prima v2 = 0.
v1’ = v1(m1 - m2)/(m1 + m2)
v2’ = 2v1 m1/(m1 + m2)
Poi assumiamo che m1 << m2, ossia:
m1 +/- m2 ~ +/-m2
da cui:
v1’ ~ - v1
v2’ << v1
la seconda si ricava facilmente pensando alla quantità 2m1/(m1 + m2) ~ 2m1/m2 << 1
Direi che possiamo fermarci qui. Potete ovviamente fare tutti gli esempi che volete, ma ricordatevi di eseguire tutto secondo una sola linea, la direzione di entrambe le velocità delle due sfere.
Inserisco la Fig. 2 dove sono riportati due giochi molto famosi. Il secondo è quello delle tante palline sospese e tutto sta nel sollevare la prima, lasciarla andare, e vedere che cosa succede. La prima si riferisce al “celebre” clic-clac del 1971. Quanti lividi sulle mani! Entrambe sono strettamente legate alla problematica trattata in questo articolo. Ovviamente saprete dirmi perché…

Mettiamo le mani avanti sui vettori
Una prefazione a ciò che dirò adesso. Non sarebbe stato difficile renderlo abbastanza semplice e intuitivo passando subito alla MQ. Tuttavia, le leggi di conservazione dell’energia e della quantità di moto sono troppo importanti nello stabilire un contatto diretto e apparentemente logico tra il mondo fisico che ci circonda e quello un po’ pazzo e assurdo della MQ. In altre parole, anche Alice usa spesso un linguaggio che riusciamo a comprendere. Un’occasione ghiotta che sicuramente non potevamo perderci.
Il problema è che il gioco del biliardo giocato su una sola dimensione (come fatto precedentemente) riesce a essere descritto abbastanza bene con espressioni matematiche di “basso” livello (somme e moltiplicazioni e poco altro). La situazione si complica abbastanza quando l’urto non è centrale e il moto delle due palle dopo l’urto segue direzioni diverse. Siamo nel caso della descrizione a due dimensioni. Essa è sicuramente la più interessante per i giocatori del tavolo verde, ma anche per le particelle del microcosmo. Potevo far trenta e non fare trentuno? Ho deciso quindi di affrontarla, anche se non si riesce ad arrivare alla soluzione del problema in quanto sarebbe necessario introdurre un parametro supplementare che complicherebbe davvero troppo le formule.
Tuttavia, l’importante per il mondo di Alice non è tanto arrivare a una soluzione, quanto impostare nel modo corretto le equazioni che derivano dalle due leggi di conservazione. E a questo punto “dovevo” arrivare.
Qual è la vera difficoltà della trattazione che ho deciso di proporvi? Presto detto: l’introduzione dei vettori e della loro scomposizione nelle due componenti lungo gli assi x e y. Questo comporta un po’ di geometria e una buona dose di trigonometria spicciola. Qualcosa in più di quanto fatto nella serie dedicata alla matematica. Nel libro “La Fisica addormentata nel Bosco” è spiegato ampiamente cosa sono i vettori e come ci si deve comportare per calcolarne le componenti e determinare il vettore somma e differenza. Non posso ripetere qui tutti i concetti relativi, ma almeno accennare alla problematica e permettervi di utilizzarla con un minimo di fatica mentale.
Il vero punto chiave da capire è che energia cinetica e quantità di moto sono grandezze decisamente differenti da un punto di vista fisico. La prima è un numero, uno “scalare”, che si calcola conoscendo solo il valore del modulo della velocità (oltre alla massa, ovviamente), dove per modulo si intende il valore numerico associato a un vettore (fatemi dire la sua intensità). La quantità di moto è invece un vettore vero e proprio, dato che tale è la velocità. Esso è quindi identificato non solo dal suo modulo, ma anche da una direzione e da un verso. In altre parole, una certa velocità di modulo v, può essere disegnata comunque nel piano del foglio, girandola e spostandola come si vuole. Il suo valore numerico rimane sempre lo stesso, ma il vettore cambia continuamente. Vediamo quanto detto nella Fig. 3. I vettori v, v1 e v2 sono diversi, pur avendo lo stesso modulo v.
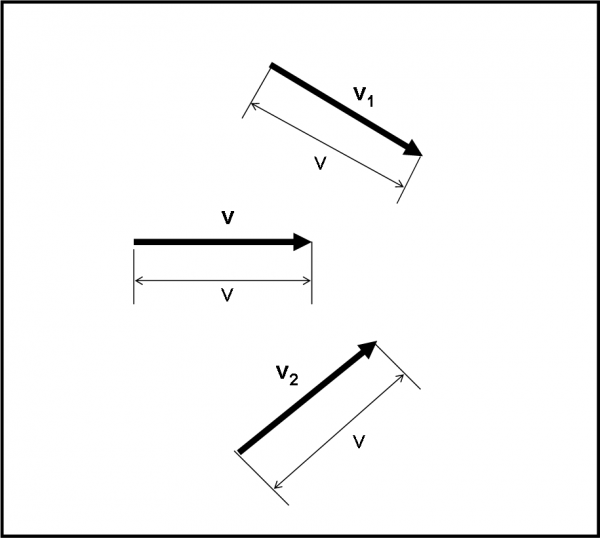
Perché nell’articolo precedente non avevo fatto distinzione tra vettore e modulo? Presto detto: l’urto avveniva lungo una sola direzione e nella stessa direzione potevano muoversi le due sfere. Sommare o sottrarre due vettori che stanno sulla stessa retta porta automaticamente alla somma o alla differenza dei moduli dei vettori. Era, quindi, del tutto inutile introdurre un concetto supplementare. Andando, adesso, nel piano della figura, non posso più tralasciare il concetto di velocità intesa come vettore. Per distinguere subito i vettori dai numeri, i primi saranno i soli a essere scritti in grassetto.
Sì, lo so, queste cose le conoscete bene se avete seguito gli articoli sul momento angolare. Tuttavia, anche chi li ha digeriti perfettamente bene non si lamenterà se lo costringo a fare un piccolo ripasso.
Sommiamo i vettori e calcoliamo le componenti
Affrontiamo, quindi, il problema della somma di due vettori e di come si utilizzano le loro componenti per avere espressioni composte da numeri. A seguito di un urto non frontale (ossia tale che la direzione della prima palla non passi per il centro della seconda) le due sfere seguono percorsi diversi. Facciamo subito una semplificazione, che -comunque- tale non è dato che si può sempre cambiare il sistema di riferimento in cui si descrive l’urto. Immaginiamo che la seconda sfera sia immobile e che si muova solo la prima. Dopo un urto non frontale (e ci torneremo sopra tra poco) le due sfere si muovono entrambe seguendo percorsi diversi. In altre parole, un vettore velocità (e quantità di moto), diretto lungo un asse, si divide in due vettori che formano un certo angolo fra di loro. La conservazione della quantità di moto assume, allora, una forma ben più generale, ossia:
m1v1 + m2v2 = m1v1’ + m2v2’
che, con l’ipotesi della seconda sfera immobile (v2 = 0), diventa:
m1v1 = m1v1’ + m2v2’
Notate i termini in grassetto, che indicano chiaramente che stiamo lavorando con vettori . La relazione precedente ci dice che un vettore diretto lungo una certa direzione (prima dell’urto) è uguale alla somma di due vettori diretti in direzioni diverse tra di loro e diverse dalla direzione della prima palla. L’uguaglianza è permessa dalla conservazione della quantità di moto. In realtà, i vettori velocità sono moltiplicati per un numero (la massa), ma questo non cambia la situazione, dato che un vettore moltiplicato per uno scalare rimane un vettore che ha la stessa direzione di quello precedente e anche lo stesso verso (la massa è sempre positiva). Ciò che cambia è solo il modulo, ossia la parte numerica, che non pone alcun problema.
In generale la somma di due vettori può essere sintetizzata (Fig. 4) da:
r = r1 + r2
Potremmo dire che vale anche r = r1 + r2, come fatto la volta scorsa lavorando su una sola dimensione? Ossia, potremmo passare da una somma di due vettori alla somma dei loro moduli? Assolutamente NO. Il vettore somma di due vettori NON ha come modulo la somma dei moduli dei due vettori. Questo capita solo se i vettori giacciono tutti su una stessa retta. Ora non più. Dobbiamo, perciò, imparare a sommare due vettori e a determinare il modulo del vettore somma. Solo così potremo scrivere una relazione vettoriale attraverso qualcosa di numerico che esprima la conservazione della quantità di moto in maniera “calcolabile”.
Limitiamoci qui a ricordare soltanto la regola del parallelogramma, ossia il metodo rapido, geometrico e veloce per determinare la somma di due vettori e il valore del modulo del vettore somma.
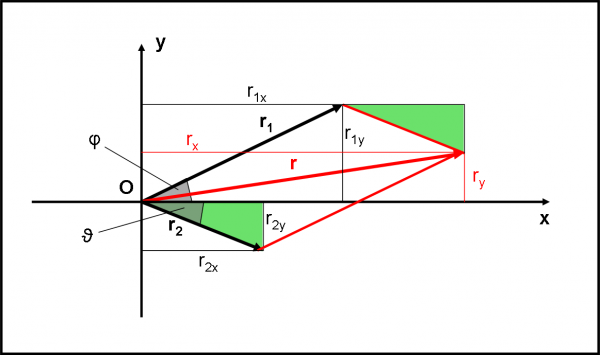
La somma dei vettori r1 e r2 si ottiene costruendo il parallelogrammo rosso. Il vettore rosso è proprio il vettore somma. Il suo modulo si ottiene considerando le componenti r1x, r1y e r2x, r2y dei due moduli r1 e r2 . Risulta:
rx = r1x + r2x
ry = r1y + r2y …. (7)
e, infine:
r = (rx2 + ry2)1/2
il modulo del vettore somma è dato, quindi, dalla radice quadrata dei quadrati delle sue componenti x e y, che si ricavano dai moduli dei due vettori iniziali attraverso la (7). Ribadisco ancora che non vale, quindi, la semplice relazione r = r1 + r2, che ha senso soltanto quando i due vettori giacciono sulla stessa retta.
La (7) si ricava facilmente considerando l’uguaglianza dei triangoli verdi. Rifletteteci sopra e riuscirete a dimostrarlo da soli.
La relazione (7) si esprime molto meglio attraverso le funzioni trigonometriche seno e coseno. In particolare, si ha che:
r1x = r1 cos φ
r1y = r1 sen φ
r2x = r2 cos ϑ
r2y = - r2 sen ϑ
Da cui segue:
rx = r1 cos φ + r2 cos ϑ
ry = r1 sen φ - r2 sen ϑ …. (8)
Sì, lo ammetto, questa parte è sicuramente un po’ impegnativa (ma potete riuscire a seguirla, ne sono sicuro). Tuttavia, spiegarla meglio vorrebbe dire allargare il discorso in modo notevole. Sono sicuro che, andando a rileggere con attenzione la definizione delle funzioni trigonometriche, le formule precedenti risulteranno più che comprensibili.
La conservazione della quantità di moto si fa in due
Adesso, però, torniamo alle nostre palle di biliardo. Cosa c’entra con loro tutto il discorso fatto sulla somma e sulle componenti dei vettori? Moltissimo. La conservazione della quantità di moto espressa da una relazione vettoriale (m1v1 = m1v1’ + m2v2’) può essere scomposta in due relazioni scalari (numeriche) relative alle due componenti dei moduli dei vettori secondo l’asse x e l’asse y, utilizzando le relazioni scritte per r1 e r2.
Una relazione vettoriale porta a due relazioni scalari, che si ottengono separando la componente x da quella y.
Non più due equazioni (le leggi di conservazione), ma tre equazioni: due provenienti dalla conservazione della quantità di moto e una da quella dell’energia cinetica. Purtroppo, però, non bastano per risolvere completamente il problema. Infatti le incognite sono quattro (le componenti delle velocità delle due sfere dopo l’urto v1x’, v2x’, v1y’ e v2y’), mentre le equazioni che le legano sono solo tre. Niente da fare, è necessario sapere qualcosa di più… Tuttavia, noi non siamo veramente interessati a risolvere il problema (non dobbiamo vincere un trofeo di biliardo), ma solo a scrivere le equazioni che stabiliscono il problema.
Scriviamo allora le tre equazioni derivanti dalle leggi di conservazione e ragioniamoci sopra.
Nessun problema per l’energia cinetica
½m1v12 + ½ m2v22 = ½ m1v1’2 + ½m2v2’2
Questa relazione non cambia passando da una rappresentazione a una dimensione a una rappresentazione a due, dato che le velocità compaiono solo con il loro modulo e non ci importa quali siano le loro direzioni e il loro verso.
Per quanto detto all’inizio possiamo eliminare il secondo termine di sinistra, dato che abbiamo assunto la seconda palla ferma (v2 = 0). La relazione diventa
½ m1v12 = ½ m1v1’2 + ½ m2v2’2
La conservazione della quantità di moto è invece data da:
m1v1 + m2v2 = m1v1’ + m2v2’
La relazione vettoriale si trasforma nelle due espressioni numeriche (ossia scalari) delle sue componenti:
m1v1x + m2v2x = m1v1x’ + m2v2x’
m1v1y + m2v2y = m1v1y’ + m2v2y’ …. (9)
Possiamo fare qualche semplificazione. Innanzitutto la velocità v2 è uguale a zero e quindi lo sono anche le sue componenti (v2x = v2y = 0). Inoltre la velocità v1 è diretta proprio lungo l’asse x e quindi la sua componente secondo y è anch’essa uguale a zero (v1y = 0, v1 = v1x).
Le (9) diventano:
m1v1 + 0 = m1v1x’ + m2v2x’
0 + 0 = m1v1y’ + m2v2y’
Le due leggi di conservazione ci danno quindi le tre equazioni (scalari):
½ m1v12 = ½ m1v1’2 + ½ m2v2’2
m1v1 = m1v1x’ + m2v2x’
0 = m1v1y’ + m2v2y’ …. (10)
Non illudiamoci di aver semplificato abbastanza per poter risolvere il problema. Le incognite sono sempre quattro e le equazioni tre. Ormai ci siamo e facciamo l’ultimo passo, di tipo trigonometrico. Le componenti delle due velocità finali possono essere scritte in funzione del modulo delle due velocità post-urto e dell’angolo che esse sottendono rispetto all’asse x (φ e ϑ) attraverso le (8).
Le (10) diventano:
m1v12 = m1v1’2 + m2v2’2
m1v1 = m1v1’cos φ + m2v2’cos ϑ (componente x)
0 = m1v1’sen φ – m2v2’sen ϑ (componente y) …. (11)
Non illudiamoci di avere come incognite soltanto i moduli delle velocità dopo l’urto (v1’ e v2’) e di poter risolvere il problema. Compaiono, infatti, due angoli che sono entrambi sconosciuti.
Su, non arrabbiatevi. L’uso delle funzioni trigonometriche è più che normale nelle equazioni e porta a grandi semplificazioni pratiche e concettuali. Dobbiamo entrare in quest’ottica prima o poi. Basta rifletterci un po’ sopra e i passaggi fatti appariranno veramente banali: basta ricordarsi la definizione di seno e coseno e poco di più…
Le equazioni (11) sono quelle che ci servono per cambiare il tavolo da gioco. Tuttavia, usiamole ancora un attimo per illustrare un caso particolare che è poi quello normale nel gioco del biliardo. In esso le due sfere sono uguali e hanno la stessa massa, ossia m1 = m2 = m. Proviamo a scrivere le nuove relazioni. Anzi, possiamo scriverle per quello che sono, senza passare alle componenti e alle funzioni trigonometriche. Sono o non sono un “buono”?
mv1 = mv1’ + mv2’ (somma vettoriale che vale due relazioni scalari)
mv12 = mv1’2 + mv2’2 (ho eliminato il fattore ½ comune a tutti i fattori)
Beh… “m” è sempre la stessa e si può eliminare tranquillamente:
v1 = v1’ + v2’
v12 = v1’2 + v2’2
Queste due relazioni hanno un significato ben più profondo di quanto possa sembrare a prima vista. La prima ci dice che il vettore v1 è proprio la somma dei vettori v1’ e v2’. In altre parole, ci dice che vale la regola del parallelogramma che abbiamo visto nella Fig. 4. La seconda è ancora più importante, anche se lavora solo sui moduli. La riconoscete? Sicuramente sì. Non è altro che il teorema di Pitagora! Non solo i due vettori v1’ e v2’ danno coma somma il vettore v1, ma i loro moduli soddisfano il teorema di Pitagora, ossia il triangolo OAB è rettangolo (Fig. 5)! Notate che i vettori sono stati scritti in grassetto, mentre i loro moduli no.
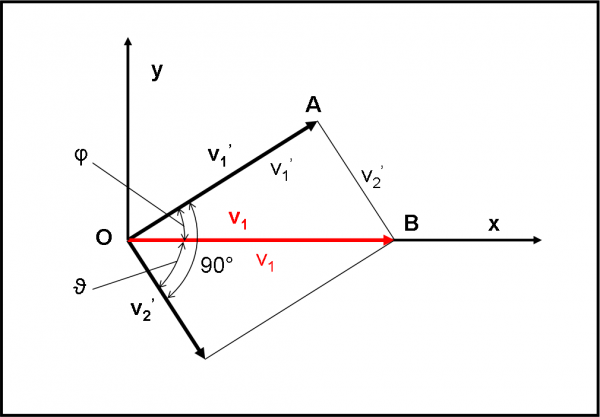
Questo vuole anche dire che la somma di φ e di ϑ vale 90° gradi. Esprimiamo queste considerazioni attraverso poche parole e la Fig. 6. Quando le due sfere si toccano, la seconda si muove lungo la direzione indicata dalla congiungente i centri delle due sfere. La prima è, invece, costretta a muoversi lungo una linea perpendicolare a quella precedente. Ribadiamo, ancora, che questa situazione è valida solo se le masse sono uguali. In caso contrario il triangolo non è più rettangolo e la somma degli angoli non è più 90°. Beh, se non altro abbiamo imparato a colpire la palla ferma e a intuire dove andranno entrambe… Se falliamo come fisici quantistici ci daremo al … biliardo!
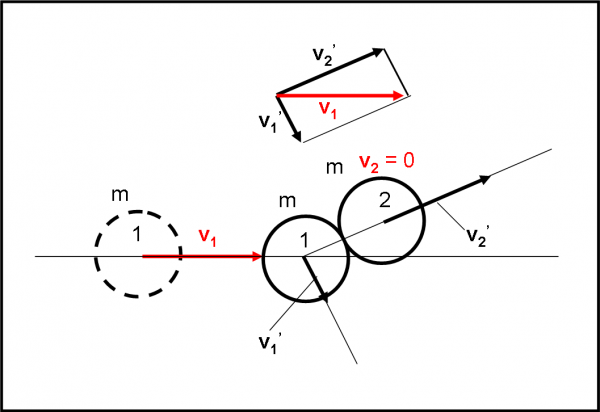
Un biliardo microscopico
Nel tavolo da gioco delle particelle le masse sono qualcosa di ben diverso e non ha nemmeno senso parlare di massa “costante” quando si è nel regime della velocità della luce. Le masse diventano relativistiche e il loro significato ben più complesso, soprattutto per il fotone.
Siamo finalmente pronti a fare il viaggio attraverso un microscopio dinamico eccezionale che ci porti nel mondo della meccanica quantistica. Vediamo, un po’ alla volta, come l'urto tra le palle da biliardo descritto dalla (11) si trasformi in qualcosa di ben diverso. Tuttavia, il concetto di base è simile e valgono sempre le stesse leggi di conservazione. Questo è il punto chiave di tutto il discorso fatto fin qui.
Parliamo dell’effetto Compton, ma poi vedremo come esso rientra in un discorso ben più generale che contiene sia l’effetto fotoelettrico che la dispersione della luce nell’atmosfera terrestre che ci fa vedere il cielo blu. Capiremo che, in fondo, è solo una questione di energia che si dà alla palla che comanda il gioco sul tavolo verde.
Diamo risalto a un concetto fondamentale: “Perché questi urti tra particelle acquistano un’importanza così grande nella storia della meccanica quantistica?” Facile rispondere. I giocatori, o meglio le sfere in gioco, sono il fotone e l’elettrone. Se il secondo potevamo anche immaginarcelo come corpo solido e concreto, lo stesso non era certo ovvio per il fotone. La luce era pensata come onda. Il fatto che si comportasse come una particella solida dotata di una certa quantità di moto e di energia implicava una visione a dir poco rivoluzionaria. In altra parole, un’ulteriore prova del comportamento ambiguo delle particelle, a volte onde e a volte corpuscoli come perfettamente evidenziato dall’esperimento delle due fenditure di Feynman, che ormai conosciamo molto bene.
Se l’effetto fotoelettrico sembra più vicino a uno sparo che faccia schizzare un frammento da una superficie solida, l’effetto Compton assomiglia molto di più a un colpo del gioco del biliardo: entrambe le sfere proseguono il loro cammino seguendo le regole definite precedentemente nel caso dell’urto a due dimensioni.
Facciamoci aiutare dalla Fig. 7 per una visione qualitativa e dalla Fig. 8 per una descrizione più accurata.
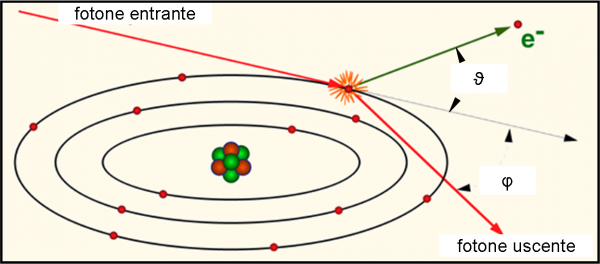
Un’onda luminosa colpisce un atomo e, in particolare, uno dei suoi elettroni più esterni. L’onda, a questo punto, non va più considerata come tale, ma come una piccola sfera dotata di massa e velocità (un quanto energetico...). Essa trasferisce parte della sua energia cinetica all’elettrone, riesce a staccarlo dall’atomo e a smuoverlo dalla sulla sua orbita. Esso diventa libero (e l’atomo si ionizza) e si muove in una certa direzione (come sappiamo bene dalla trattazione di meccanica classica precedente). Anche il fotone, però, continua la sua corsa (diversamente dall’effetto fotoelettrico) anche se con un energia diversa (la velocità è però sempre la stessa, quella della luce). Ciò che cambia in lui è la lunghezza d’onda e la direzione dello spostamento. Perdita di energia vuol dire allungamento della lunghezza d’onda (arrossamento) e spostamento rispetto alla direzione originale vuol dire dispersione o scattering.
Ecco perché l’effetto viene anche chiamato scattering Compton. Cosa si vede in realtà? Si nota un cambiamento della lunghezza d’onda della luce che può essere spiegata solo e soltanto attraverso un urto tra particelle. Uno dei capisaldi della meccanica quantistica! La Fig. 7 ci descrive qualitativamente lo scattering Compton, che dà luogo a uno spostamento dell’elettrone e a un indebolimento energetico del fotone, rivelabile attraverso l’allungamento della lunghezza d’onda.
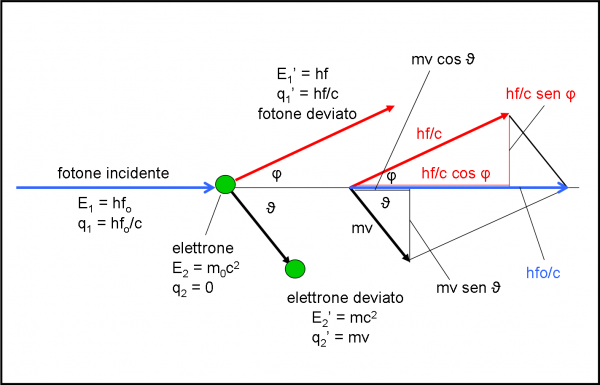
Ci può bastare la Fig. 7, dopo tutte le formule che abbiamo scritto per gli urti? Direi proprio di no e tentiamo allora di riscrivere le stesse formule nel caso dell’effetto Compton, utilizzando la più quantitativa Fig. 8, dove nella parte destra c’è proprio lo schema geometrico che descrive i vettori e le loro componenti. Il fotone prima dell’urto dà luogo a un “vettore” blu, mentre dopo l’urto a uno rosso. Ho scelto questi colori per evidenziare l’allungamento della lunghezza d’onda. C’ho pensato a lungo, ma penso proprio che siate in grado di seguire tutto il ragionamento. Un bel colpo, in quanto riusciamo a descrivere un fenomeno quantistico attraverso le leggi di un biliardo. Niente male!
Riscriviamo, allora, le equazioni (11):
m1v12 = m1v1’2 + m2v2’2
m1v1 = m1v1’cos φ + m2v2’cos ϑ (componente x)
0 = m1v1’sen φ – m2v2’sen ϑ (componente y) …. (12)
Dobbiamo eseguire qualche sostituzione. La velocità del fotone è conosciuta, ma non la sua massa. Anzi, esiste oppure no? Non nel senso che noi diamo normalmente a questa grandezza fisica, ma in termini quantistici sicuramente sì.
Beh, innanzitutto devo inserire nuovamente l’energia della seconda palla, dato che il fatto di stare ferma non annulla la sua energia. Un elettrone ha una sua energia anche da fermo…
Quanto vale? Beh… ce lo dice Einstein: E = moc2, dove mo è la massa a riposo dell’elettrone. Ricordiamo anche che se esso si muove la sua massa relativistica cambia secondo la legge;
m = mo/(1- v2/c2)1/2
Una vecchia formula che potete prendere per quello che è o comprendere molto meglio andando a leggere i primi articoli sulla dinamica relativistica.
Qual è l’energia del fotone in termini quantistici? Essa è data dalla frequenza moltiplicata per la costante di Planck (cosa già nota attraverso la storia dell'atomo), ossia:
E = hfo
Come vedete non compare esattamente la massa, che non esiste, ma l’importante è che si possa scrivere l’energia del fotone. In questo modo possiamo tranquillamente conservare l’energia totale.
La prima equazione della (12) diventa:
hfo + moc2 = hf + mc2 (m è dato dalla formula precedente)
Dove f è la frequenza dopo l’urto. Passiamo, adesso alle due equazioni relative alla conservazione della quantità di moto.
L’energia del fotone è hfo. Se vogliamo la sua quantità di moto basta dividerla per la velocità, ossia c. Abbiamo quindi che la quantità di moto del fotone non è altro che hfo/c (banale!). Quello dell’elettrone è invece dato dal solito prodotto mv, dove però m è la massa relativistica. L’elettrone è proprio una piccola palla di biliardo. Le due equazioni diventano:
hfo/c = hf/c cos φ + mv cos ϑ
0 = hf/c sen φ – mv sen ϑ
Mettendo tutto insieme abbiamo:
hfo + moc2 = hf + mc2
hfo/c = hf/c cos φ + mv cos ϑ
0 = hf/c sen φ – mv sen ϑ
In fondo è cambiato ben poco, come concetto, anche se le grandezze che compaiono sono “leggermente” diverse.
Cosa si osserva in pratica? Non certo lo spostamento delle sferette o cose analoghe al biliardo. Ciò che si osserva è il cambiamento della lunghezza d’onda del fotone (ossia della luce che urta un atomo). Nelle equazioni, la lunghezza d’onda compare attraverso il suo inverso, la frequenza f. Vi evito una serie un po’ noiosa di passaggi matematici (chi vuole provarci può tentare, ma non mi chieda poi di raccontarlo a tutti… mi sembrerebbe eccessivo… almeno per adesso!) e scrivo subito il risultato:
Δλ = λ – λo = λc (1- cos φ)
Dove la quantità:
λc = h/moc
prende il nome di lunghezza d’onda di Compton ed è una costante che vale circa 2,4 · 10-12 m.
Essa permette di calcolare l’arrossamento della luce, ossia la differenza tra lunghezza d’onda dopo l’urto (λ) e quella iniziale (λo).
Ribadisco, che questo risultato osservativo può essere spiegato solo e soltanto attraverso una natura corpuscolare del fotone, ossia attraverso una sua interpretazione quantistica.
Vorrei concludere con un riassunto piuttosto semplificato, ma che può darvi un’idea della differenza tra vari fenomeni di scattering. Consideriamone tre, i più conosciuti.
Questione di energia
Il gioco è sempre lo stesso, con due palle da biliardo formate da un fotone e da un elettrone. Ciò che veramente cambia è l’energia che si trasmette nell’urto.
Il primo scattering è quello di Rayleigh. Esso è quello che comanda la visione azzurra del cielo. Ne avevamo già parlato QUI, ma possiamo ridefinirlo molto semplicemente. I fotoni che colpiscono gli atomi atmosferici vengono deviati, ossia diffusi, e questo capita soprattutto per le lunghezze d’onda più corte come quella del blu. L’energia in gioco è bassa e l’elettrone non è minimamente scalfito dall’urto. E’ il fotone che ne risente, ma solo per il cambiamento della sua direzione. Non perde alcuna energia. Questo effetto è servito ben poco alla meccanica quantistica, dato che la spiegazione può essere data tranquillamente attraverso la natura ondulatoria della luce. I fotoni potevano anche non esistere come particelle.
Se l’energia cresce il fotone scarica tutta la sua violenza sull’elettrone e riesce a staccarlo dalla sua posizione ancorata al nucleo atomico. Del fotone non si ha più memoria (ha dato tutto quello che aveva), ma nasce un elettrone libero che ci mostra l’effetto fotoelettrico. Esso si ottiene per valori di energia del fotone di poco superiori all’energia di legame dell’elettrone con il nucleo.
Per energie ancora superiori il fotone non solo riesce a staccare e a spostare l’elettrone, ma continua la sua corsa anche se molto più stanco e arrossato, allungando la sua lunghezza d’onda. Questo è, ovviamente, l’effetto Compton. L’energia del fotone è molto più grande dell’energia di legame e l’elettrone può essere considerato “libero” fin da subito.
Esiste anche un quarto effetto (di coppia) che nasce per energie ancora superiori, dove l’urto scompagina lo stesso nucleo atomico scagliando all’esterno un elettrone e un positrone, ma non esageriamo…
La faccenda non è veramente così semplice, dato che conta anche il tipo di atomo coinvolto e molte altre cose. Prendetela come una spiegazione molto qualitativa che serve, tuttavia, a farsi un’idea molto generale e intuitiva.
L’effetto Compton è valso anch’esso il Nobel nel 1922.
Beh… se siete riusciti a seguire tutto, senza spaventarvi, siete proprio bravi!
L’effetto inverso
Vale la pena accennare all’effetto Compton inverso. Esso è estremamente importante in quanto si nota benissimo nel rumore cosmico di fondo. Esso avviene quando l’energia del fotone è molto più piccola di quella dell’elettrone. In questo caso è possibile produrre fotoni ad altissima energia. Un esempio è proprio l’interazione tra un raggio cosmico (elettroni a grandissima energia) che si scontra contro i fotoni della radiazione cosmica di fondo. Questo effetto è decisamente impossibile da ottenere in un tavolo da biliardo, dato che implicherebbe che la nostra palla venga accelerata dall’urto contro una palla apparentemente immobile. Tuttavia, lasciamo alla MQ qualche freccia in più nel suo arco.
Attenzione: Ribadisco ancora che chi seguito la QED, è sicuramente in grado di disegnare sia l'effetto fotoelettrico che quello Compton attraverso semplici diagrammi di Feynman. Gira e rigira, tutto si allaccia a tutto. Che meraviglia la fisica, sia quella classica che quella quantistica!
La base di "Tutto": il PRINCIPIO D'INDETERMINAZIONE DI HEISENBERG
Uno dei capisaldi della meccanica quantistica (forse la base di tutto o quasi) è sicuramente il principio di indeterminazione di Heisenberg. L'abbiamo già trattato nella QED, ma vale la pena riproporlo riallacciandoci soltanto all'ottica classica. Il principio deve esistere e valere anche nel mondo "normale". Solo che spesso non ce ne accorgiamo...
Prima di cominciare consiglio di andarvi a rileggere la diffrazione luminosa per inquadrare meglio il problema, anche se certe cose potreste accettarle senza troppe spiegazioni. Ne approfitterò anche per chiarire meglio cosa s’intenda per “disturbo” dovuto alla misura che spesso porta a grandi confusioni (non solo da parte degli inesperti…).
Bando alle ciance e cominciamo.
Il principio di indeterminazione di Heisenberg dice in modo molto conciso e semplificato: “E’ impossibile misurare con la stessa precisione sia la posizione che la velocità di una particella”. In altre parole: “Quanto più si tenti di stabilire con maggiore accuratezza la posizione occupata da una particella, tanto più diventa aleatoria e incerta la sua velocità”. Potremmo dire, molto semplicemente, che il principio è di banale comprensione, sapendo ormai che una particella non occupa una certa posizione nello spazio, ma ha solo una certa probabilità di essere in un dato punto. Tuttavia, la risposta farebbe storcere un po’ il naso, dato che la faccenda può apparire sensata nella sua illogicità, ma non risulta molto chiaro il perché e il percome di questa conseguenza. Intuitivamente è accettabile, ma sarebbe molto meglio esprimere il concetto con una qualche esperienza diretta.
Potremmo cavarcela utilizzando un ragionamento legato alla fisica classica.
Per potere accertare la reale posizione di una particella devo innanzitutto vederla molto bene, ossia illuminarla. Ma illuminare qualcosa vuol dire inviare un fascio di fotoni che sicuramente disturba il movimento della particella. In altre parole, per misurare la posizione di una particella, con una precisione elevata, bisogna ricorrere a una luce di lunghezza d'onda molto corta, e quindi altamente energetica. Ciò si traduce nel trasferimento di una certa quantità di moto (massa per velocità) alla particella e pertanto non è possibile misurare con esattezza la sua velocità. Alternativamente, se ci si accanisce sulla misura di quest’ultima, diventa problematico descrivere esattamente la sua posizione. Un fenomeno prettamente meccanico.
Troppo spesso nei libri e in vari articoli di pseudo-scienza ci si ferma a questa spiegazione. Essa, anche se sicuramente vera in linea di principio, ha ben poco a che fare con la MQ. In realtà, anche se riuscissimo a “vedere”, senza interagire, la situazione non cambierebbe di molto. L’impossibilità di misurare entrambe le grandezze fisiche dipende essenzialmente dalle caratteristiche quantistiche intrinseche delle particelle. Il fatto che esse siano rappresentabili come onde di probabilità implica proprio che è impossibile sapere dove sia realmente la particella o -alternativamente- se si riesce a localizzarla perfettamente (in altre parole la facciamo collassare) diventa del tutto aleatoria la sua velocità.
Sì, lo so, potrei anche considerarmi soddisfatto e limitarmi alle parole, come si fa di solito e magari inserire una formuletta che lega posizione e velocità (o meglio quantità di moto) alla costante di Planck (che già conoscete). Lo farò di sicuro, ma preferisco arrivarci proseguendo lungo il tracciato aperto da Feynman e rifarmi all’esperienza della fenditura.
Questa volta, però, ne consideriamo una sola: ci basta e avanza. Qualcuno potrebbe subito fermarmi e dire: “No, non funziona! Sappiamo benissimo che se spariamo gli elettroni o i fotoni attraverso una sola fenditura non otteniamo assolutamente la figura d’interferenza tipica delle onde. D’altra parte è ovvio, dato che se abbiamo una sola fenditura sappiamo benissimo da dove deve passare la particella e quindi essa collassa proprio nello stato di particella”. In parte, avrebbe anche ragione, ma non del tutto. Dimenticherebbe il fenomeno della diffrazione…
Essa è quel fenomeno che ci vieta categoricamente di poter vedere al telescopio una stella come un oggetto puntiforme. La luce, intesa come onda, che passa attraverso una fenditura, deve toccare anche i bordi del foro e questi danno luogo a una nuova onda che interferisce con quella originatasi nell’altro bordo. In conclusione, l’immagine che si ottiene è ancora una figura d’interferenza con un picco di luminosità centrale molto alto, seguito da zone scure e chiare di altezza decrescente. La situazione, quindi, è ancora perfetta per dimostrare sperimentalmente il principio d’indeterminazione.
Richiamiamo brevemente il fenomeno della diffrazione che, per semplicità, possiamo legare soltanto all’esistenza dei bordi della fenditura (il principio di Huygens andrebbe ancora più in là, ma le conclusioni sarebbero le stesse).
Immaginiamo di avere un’onda luminosa proveniente dall’infinito (quella di una stella, ad esempio), ma realizzabile anche con una strumentazione da laboratorio. Essa può essere rappresentata come linee rette parallele alla parete della fenditura. Se preferite, però, potete anche pensare a fotoni “sparati” in modo perfettamente perpendicolare alla parete: o entrano nella fenditura oppure non entrano, non ci sono vie di mezzo, tipo strani rimbalzi.
I principi dell’ottica, ma anche una visione terra-terra, ci dice che l’onda (o il fotone…) che “tocca” la parete dà luogo a una nuova onda (se volete, chiamatela anche probabilistica) con l’origine in quel punto. Consideriamo la Fig. 1, dove vi è la solita parete con al centro la fenditura e, più lontano, lo schermo di raccolta dei fotoni.

Ciò che vediamo è che l’onda piana si trasforma in un onda “quasi” sferica. L’immagine finale sullo schermo mostra un alto picco centrale e picchi laterali sempre più bassi. Proviamo a variare la larghezza della fenditura. La matematica ci dimostra facilmente che l’intensità dell’onda che tocca lo schermo finale è una funzione della larghezza della fenditura d, della lunghezza d’onda λ della luce utilizzata e della distanza dal centro dello schermo O che si misura come angolo α rispetto al centro della fenditura. In particolare, però, vale una semplicissima relazione che possiamo anche scrivere senza paura e che ci dice quanto è larga la prima banda luminosa centrale:
α = λ/d
E’ una formula che dovreste conoscere molto bene, soprattutto coloro che posseggono un telescopio e cercano (non voi sicuramente) di ottenere immagini migliori inserendo oculari e diavolerie del genere. Niente da fare: chi comanda la nitidezza dell’immagine finale (ossia le sue dimensioni) è il diametro dell’obiettivo (ossia d). Più è grande d e più piccola è la figura di diffrazione, ossia migliore è il potere risolutivo dell’obiettivo. In realtà, dovremmo far comparire il seno di α, ma gli angoli sono così piccoli che si può anche scrivere l’angolo al posto del suo seno. In ogni modo, quello che ci interessa è il poter dire che la larghezza della figura di diffrazione (che è poi l’immagine finale) aumenta al diminuire della larghezza della fenditura.
Vediamo la situazione in Fig. 2, in cui si sono rappresentate le immagini ottenute sullo schermo finale (ossia, le curva di luminosità) per tre valori di d.
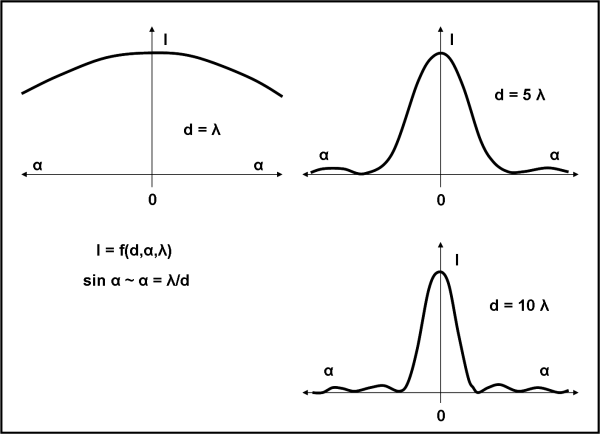
Possiamo anche schematizzare il risultato disegnando direttamente, in Fig. 3, come varia l’onda luminosa dopo aver passato la fenditura. Per il nostro scopo, è utile rappresentarla con i raggi luminosi, ossia con le rette che partono dal punto d’origine dell’onda e sono ad essa perpendicolari. Non sbaglieremmo di certo nel considerare ogni raggio luminoso come una delle possibili direzioni di ogni singolo fotone, dato che essi sono proprio rappresentabili come onde di probabilità.
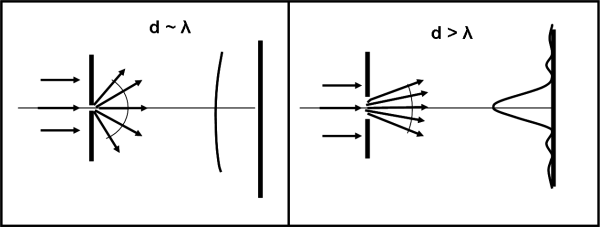
Non spaventatevi: ormai dobbiamo sapere che possiamo passare da onde alle particelle senza alcuna paura. Basta ricordare che la particella, prima di essere individuata, può benissimo essere considerata un’onda. I fotoni che escono dalla fenditura, hanno un campo di probabilità sempre più grande a mano a mano che la fenditura diminuisce, in quanto cresce l’angolo descritto dai raggi luminosi perpendicolari alla superficie dell’onda.
Questa visione, che corrisponde perfettamente ai principi dell’ottica meccanica, dimostra anche perfettamente il principio di Heisenberg. Ragioniamoci un attimo: la fenditura che decresce di dimensioni indica con sempre maggiore precisione il punto esatto dell’origine dell’onda al passaggio dalla fenditura, ossia la posizione della particella. Se, teoricamente, la fenditura diventasse puntiforme, l’onda d’uscita creerebbe un’immagine finale infinita (come vedete viviamo sempre nella continua lotta-amicizia tra zero e infinito), così come se la larghezza della fenditura tendesse a infinito, le dimensioni dell’immagine finale sarebbe puntiforme. In altre parole, se avessimo una posizione perfetta (puntiforme) della particella avremmo infinite direzioni che potrebbe seguire. Se, invece, avessimo una sola direzione perfettamente determinata, la particella potrebbe essere ovunque.
Abbiamo o non abbiamo descritto il principio d’indeterminazione di Heisenberg? Direi proprio di sì. Possiamo anche vederlo geometricamente con la Fig.4, in cui ho scelto una certa dimensione della fenditura.

Prima della fenditura, l’onda proviene dall’infinito, ossia ha i suoi raggi paralleli. Ciò vuol dire che è estremamente ben definita la direzione di provenienza e quindi anche la velocità del fotone (valore numerico, ossia c, e direzione), ma è assolutamente aleatoria la posizione del fotone che può trovarsi in un qualsiasi raggio. Ho una precisa determinazione della velocità, ma ho una scarsissima precisione nella posizione della particella che ha l’onda come rappresentazione delle sue probabilità di esistenza. So da dove proviene il fotone e con quale velocità ma non so proprio dove trovarlo: può essere ovunque.
Finalmente arriviamo alla fenditura. Tutte le posizioni del fotone che portano alla parete sono da escludere. Se fosse stato lì si troverebbe davanti una porta chiusa e si rivelerebbe collassando come particella fisica. Quelli che entrano nella fenditura possono, invece, proseguire. Tuttavia, più l’apertura della fenditura è piccola e più si determina con esattezza la posizione del fotone “fortunato”. Qualcuno potrebbe dirmi. “Sì, va bene… ma anche in questo caso il fotone collasserebbe in particella dato che sono sicuro della sua posizione”. Avrebbe ragione se la fenditura bloccasse il fotone. Invece, lui, una volta passato crea un nuova onda la cui “larghezza” (ossia l’angolo α) aumenta al diminuire delle dimensioni della fenditura. Più la fenditura è stretta, ossia più è precisa la posizione del fotone, più le direzioni possibili del fotone allargano il loro spazio disponibile (l’angolo α), come abbiamo visto in Fig. 3. Ancora, in altre parole: più è precisa la posizione del fotone e più è aleatoria la direzione che prenderà dopo il suo passaggio dalla fenditura.
Come si traduce graficamente questa situazione (non ce ne sarebbe nemmeno bisogno, ma è meglio essere rigorosi fino in fondo)? Beh… le velocità del fotone dopo il passaggio è indicata da una qualsiasi delle frecce nere di Fig. 3. Ciò che conta è l’angolo formato dai raggi “estremi” che è poi quello che deciderà la larghezza dell’immagine di diffrazione finale (ancora e sempre l’angolo α).
Come ormai sappiamo benissimo, quest’angolo aumenta al diminuire della larghezza della fenditura, ossia della precisione con cui si misura la posizione del fotone nel momento di passaggio attraverso di lei. Quale sarà l’incertezza nella sua velocità probabile? E' facile separare il vettore velocità rosso in due vettori (componenti): uno diretto perpendicolarmente allo schermo finale (e alla parete) (vy) e uno diretta lungo la parete stessa. Quest’ultimo (vx) ci indica molto bene quanto sia grande l’incertezza della direzione della velocità del fotone. Se vx fosse zero la direzione sarebbe quella precedente alla fenditura, ossia lungo l’asse y. Se vx cresce, cresce anche la possibilità del fotone di spostarsi rispetto a quella direzione. In altre parole, al crescere di vx (e quindi al diminuire della larghezza della fenditura e all’aumentare della precisione della posizione) aumenta l’incertezza nella velocità del fotone. Più esattamente, l’incertezza nella direzione della velocità è data proprio da Δvx = 2vx.
Questa conclusione è in perfetto accordo con il principio di Heisenberg; Non posso conoscere perfettamente sia la posizione che la velocità di una particella. O questa o quella per me pari NON sono
La matematica ci direbbe che, “al limite”, potrei conoscere perfettamente una delle due e non avere la benché minima idea dell’altra. In realtà, la fisica non riesce ad andare "al limite" fino in fondo, come cercava di fare Zenone con la sua tartaruga. La fisica si muove a intervalli, a “pacchetti”. In un modo o nell’altro, possiamo sempre avere un’idea di entrambe le grandezze fisiche, dato che nessuna di esse può andare realmente a zero, ma a una dimensione fisicamente quantificabile. Più aumenta la precisione della prima e tanto diminuisce quella della seconda, e viceversa.
Non vi stupirete di certo, a questo punto, che possa scrivere una formuletta semplicissima che descrive sinteticamente e perfettamente il principio di Heisenberg:
Δx Δvx ≥ h/4π
dove h non è altro che la costante di Planck, proprio quella “cosa” che ci dice che in fisica non si può andare sotto a un certo valore. Δx e Δvx sono rispettivamente gli errori nella posizione e nella velocità.In realtà, la sua scrittura esatta sarebbe:
Δx Δq ≥ h/4π
dove, al posto della velocità, vi è la quantità di moto q della particella (la “lumaca” del mio libro sulla fisica classica, io adoro questa grandezza fisica…), ossia la massa moltiplicata per la velocità. Non ditemi che per il fotone la massa è zero e quindi la quantità di moto è zero… no… no… c’entra l’energia e la velocità della luce, ossia la quantità di moto è q = E/c. Non ne siete convinti? Uffa! Ve lo dimostro subito:
q = mv
ma, per il fotone, v = c
q = mc
ma so anche che E = mc2 (lo dice il nostro amico Albert…), ossia m = E/c2 e, quindi, sostituendo:
q = Ec/c2 = E/c
Eh sì, sapere usare la matematica è veramente un aiuto incredibile per comprendere i fenomeni fisici.
Scusate la piccola digressione (sempre utile, comunque) e le continue ripetizioni nello spiegarvi l’esperimento legato al principio di Heisenberg. Ma, ormai, mi conoscete: preferisco battere e ribattere su un concetto, piuttosto che farvi andare avanti e indietro nell’articolo.
Vi consiglio questo breve, ma sorprendente, video del prof. Lewin del MIT: una prova sperimentale che spiega meglio di tante parole. Si vede benissimo come, finché la fenditura è abbastanza larga, rimanga molto indeterminata la posizione (può essere ovunque nell'apertura), mentre la velocità (ossia la direzione del movimento) sia quasi perfettamente orizzontale. Chiudendo la fenditura aumenta l'accuratezza della posizione, ma a un certo punto entra in gioco il PIH e la direzione diventa sempre più incerta.
Superare montagne insuperabili: l'EFFETTO TUNNEL
Spesso e volentieri si usa un paradosso legato alla vita di tutti i giorni per descrivere l’effetto tunnel.
Immaginiamo di trovarci davanti una lastra di metallo robustissima e impossibile da perforare. Bene, se tirassimo una pallina da tennis contro la parete potremmo spendere tutta la nostra esistenza in questo esercizio fisico ma continueremmo a vedere la pallina tornare indietro dopo aver urtato la parete. L’effetto tunnel ci dice, invece, che esiste una possibilità concreta che la pallina, prima o poi, attraversi il muro. In realtà, enunciato in questo modo, l’effetto tunnel è molto affascinante, ma è del tutto impossibile. Dobbiamo rassegnarci e cambiare pallina e parete. La parete diventa in qualche modo una parete di energia e la pallina una particella microscopica, una di quelle che hanno comportamenti ben diversi dalla realtà di tutti i giorni.
Al Luna Park
Per avvicinarci meglio alle barriere di tipo energetico facciamo un esempio ancora più calzante che ci porta in un Luna Park, sulle montagne russe, in particolare. Sappiamo benissimo che le montagne russe si basano su un principio fondamentale della meccanica classica applicato a un percorso di sali e scendi di un vagoncino. Il principio è quello della conservazione dell’energia. Chi viaggia sulle montagne russe deve conservare la sua energia.
Le energie in gioco sono solo due: l’energia potenziale e l’energia cinetica. Le dovreste conoscere molto bene, ma è meglio richiamare brevemente il loro significato. Qualsiasi oggetto che sta sulla Terra è soggetto alla gravità del pianeta ed è costretto a cadere verso il basso a meno che qualcosa non lo tenga sollevato (pensate alla mela di Newton). Se saliamo sempre più in alto rispetto al suolo e se poi ci lanciamo in balia della forza di gravità subiremo effetti sempre più disastrosi. Se saliamo su una sedia, non succede praticamente niente, ma se ci buttiamo da un ponte sospeso la faccenda diventa ben più pericolosa. Ancora peggio se ci buttiamo da un aereo a 10000 metri di quota.
Cosa vuol dire tutto ciò? Che, a mano a mano che saliamo, ossia ci allontaniamo da Terra, acquistiamo un’energia sempre più grande, proprio quella che, una volta liberata, ci fa precipitare verso il suolo. Questa energia dipende solo e soltanto dalla massa della Terra e dall’altezza a cui siamo arrivati. Essa prende il nome di energia potenziale gravitazionale e viene descritta in pratica solo dall’altezza raggiunta (la Terra è sempre la stessa per i suoi abitanti).
Torniamo, quindi, al nostro ottovolante, quando siamo fermi sul punto più alto. In queste condizioni l’energia potenziale è massima, ossia siamo pronti per eseguire un lavoro non indifferente (un lavoro che potrebbe farci schiacciare al suolo). Fortunatamente siamo in un carrello che è tenuto attaccato alle rotaie in modo perfetto e ci evita cadute catastrofiche. Quale energia possediamo nel punto più alto? Solo e soltanto l’energia potenziale, riferita solo alla posizione occupata. Ripetiamo ancora: in quel momento, con il carrello fermo, tutta l’energia che possediamo è l’energia potenziale.
Aspettiamo ancora un attimo prima di far partire il vagoncino…
L’altro tipo di energia che conosciamo molto bene nella vita di tutti i giorni si chiama energia cinetica ed è quella legata al movimento. Quando corriamo o andiamo in macchina o in treno o quello che volete, abbiamo una certa energia che è legata alla nostra massa (più siamo pesanti e più difficile è muoversi) e alla velocità con cui ci spostiamo. Se qualcuno fosse fermo lungo la strada e ci vedesse passare alla guida di una macchina potrebbe misurare la nostra velocità e, sapendo il peso totale della macchina più passeggero, misurerebbe facilmente l’energia che ha la vettura, in quell’istante.
Bene, torniamo in cima all’ottovolante. Prima di partire ricordiamoci il principio di conservazione dell’energia. Esso dice che l’energia che ha un certo oggetto, o sistema qualsiasi, deve sempre essere la stessa. Se vi sono più energie in gioco la loro somma deve rimanere costante. In poche parole se diminuisce una certa energia deve aumentare l’altra in modo che la somma resti sempre la stessa.
E’ ora di dare il via al nostro carrello. Via! Ci accorgiamo in fretta che l’energia cinetica sta cambiando drasticamente. All’inizio eravamo fermi e quindi la velocità era zero e, quindi, anche l’energia cinetica. Adesso stiamo precipitando a grande velocità e la nostra energia cinetica sta aumentando decisamente. La conservazione dell’energia, però, non può sbagliare. L’energia che stiamo guadagnando deve andare a scapito dell’altra energia che possedevamo all’inizio (l’unica), quella potenziale. In effetti è vero!
A mano a mano che scendiamo, l’energia potenziale diminuisce sempre di più, dato che diminuisce l’altezza dal suolo. La fisica non sbaglia mai: se in ogni istante della discesa facessimo la somma delle due energie troveremmo sempre lo stesso identico valore.
Finalmente, con lo stomaco in bocca, arriviamo in fondo alla discesa. L’energia potenziale è diventata zero (più in basso non possiamo andare), ma l’energia cinetica è altissima, anzi è l’unica che possediamo ed è esattamente uguale a quella potenziale che avevamo prima della partenza, lassù in cima alle montagne russe. Ci fermiamo? Assolutamente no! Siamo in balia dell’energia cinetica, un’energia di movimento. Il carrello sfrutta questa energia che abbiamo accumulato in discesa e continua a muoversi anche se il percorso è, adesso, in salita. La velocità diminuisce, ma il vagoncino continua a salire. Fino a quando?
Se non ci fossero attriti, andrebbe avanti fino a sperperare tutta l’energia cinetica. Tuttavia, mentre stiamo salendo, anche se sempre più lentamente, stiamo riguadagnando energia potenziale, dato che ci stiamo alzando rispetto al suolo. Non possiamo nemmeno dimenticare che l’energia totale deve conservarsi. Ciò comporta che quando l’energia cinetica diventa zero (ossia il vagoncino si ferma) abbiamo riguadagnato tutta l’energia potenziale che avevamo all’inizio del giro in giostra. Siamo tornati nelle condizioni iniziali, quando tutta l’energia che avevamo era quella potenziale.
La Fig. 1 mostra schematicamente quello che è successo. Scusate se ho riproposto un esempio ben conosciuto da tutti, ma per qualcuno potrebbe non essere male richiamare in modo semplificato e senza formule un classico esempio (molto divertente) di conservazione dell’energia meccanica.
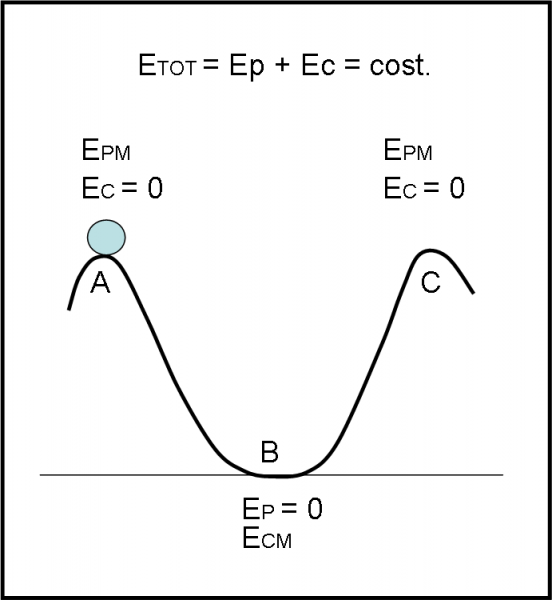
Non sarebbe, quindi, molto difficile (teoricamente) costruire un otto volante molto più complicato: l’importante è che il sali e scendi non vada mai contro questo banalissimo schema (a parte la costruzione del carrello, la tenuta delle ruote sui binari e molte altre cose legate alla sicurezza).
Il progettista che ha costruito le montagne russe della Fig. 2 è, invece, un incompetente e capisce ben poco di meccanica classica. Vi è qualche speranza che il carrello che parte da A e scende fino in B possa mai raggiungere il punto C? Assolutamente no! Quando il carrello arriva nel punto A’, ha sperperato tutta la sua energia cinetica (velocità uguale a zero) e possiede solo l’energia potenziale. Questa però, per la conservazione dell’energia, non può superare quella che aveva in A. Il carrello non può certo salire ancora perché, se lo facesse, guadagnerebbe ulteriore energia potenziale, cosa impossibile in meccanica classica. L’energia non si crea dal niente e ci dobbiamo tenere quella che abbiamo.
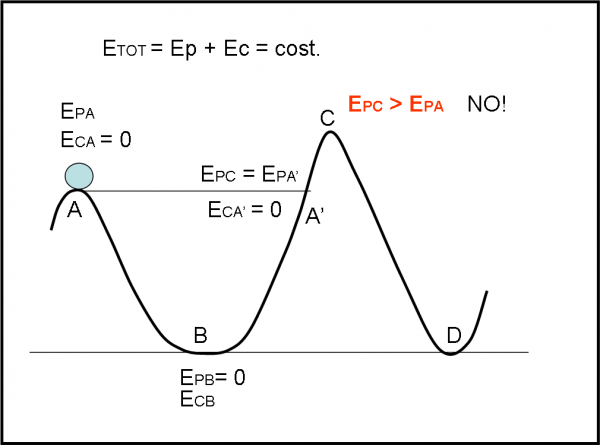
L’unica speranza per poter proseguire sarebbe la bacchetta magica di una fata o di qualche personaggio veramente speciale. Nel mondo quotidiano non esistono maghi o streghe o fate: il carrello è costretto a ricadere all’indietro verso il punto B e tornare nuovamente in A. Una giostra poco divertente… Le cose, però, possono cambiare se il nostro otto volante diventa estremamente piccolo, talmente piccolo che possa intervenire la simpaticissima Alice (del Paese delle Meraviglie), proprio la bimba che ci ha introdotto nel mondo della Meccanica Quantistica.
Barriere energetiche
Mettiamo, allora, da parte l’otto volante, ma teniamo bene a mente che l’impossibilità di arrivare fino a C rappresenta una barriera della vita quotidiana, una barriera energetica, qualcosa di molto simile alla parete che colpivamo con la pallina da tennis sperando di passarle attraverso. Per superare la barriera o arrivare fino alla cima della giostra, in C, il problema è lo stesso: bisogna essere in grado di superare una barriera energetica, ossia riuscire ad avere in regalo dell’energia che la meccanica classica non può assolutamente darci.
Abbiamo cambiato scenario, siamo diventati piccolissimi e riusciamo a vedere gli atomi. Che belli, con quel loro nucleo e tutti quegli elettroni che gli girano attorno, al pari di api attorno a un alveare. In realtà, assomigliano molto a delle api. Sembra di vederli. Esprimiamoci meglio. Siamo sicuri che ci siano, ma non è assolutamente facile vederli. Dobbiamo accettare la verità: sappiamo che gli elettroni ci sono, ma dobbiamo ammettere di non vederne nemmeno uno. Sicuramente vanno troppo veloci. Se ci fissiamo su una certa posizione, dove sappiamo che l’elettrone deve sicuramente esistere, non lo vediamo perché non sappiamo assolutamente la traiettoria che sta seguendo, ossia, parlando seriamente, non conosciamo la sua quantità di moto. Se invece riusciamo a calcolare esattamente quest’ultima quantità, perdiamo completamente la possibilità di stabilirne la posizione.
Bene, è inutile proseguire, sapete bene di cosa parlo: di uno dei principi fondamentali del mondo di Alice, ossia il Principio di Indeterminazione di Heisenberg, che ci dice che non si possono conoscere accuratamente la velocità e la posizione di una particella. Gira e rigira questo principio è sempre pronto a romperci le scatole. Lo ha fatto nell’esperimento delle due fenditure, lo fa nella definizione del modello atomico attraverso gli orbitali e continua a farlo in mille altre situazioni.
Per chi non fosse già amico intimo del mondo di Alice, faccio un esempio molto intuitivo del principio di Heisenberg, uno dei capisaldi di tutta la MQ e non solo (ci servirà ancora molto). Supponiamo di avere un segnale che varia nel tempo, proprio come un'onda, e che si voglia sapere, in un certo istante, la frequenza esatta del segnale. Purtroppo, è impossibile! Infatti, per poter determinare la frequenza, è necessario seguire il segnale per un certo intervallo di tempo, almeno coprire un periodo dell’oscillazione. Facendo così, però, si perde automaticamente la precisione dell’istante in cui si ottiene l’informazione. Insomma, o si ha l’istante preciso o si ha la frequenza. Non si possono avere entrambi… Lo stesso concetto vale per la quantità di moto (o velocità) e la posizione o per il tempo e l’energia.
Esprimiamolo attraverso una semplice formuletta:
dx dq ≥ h/4π
dx è l’errore commesso sulla posizione e dq quello commesso sulla quantità di moto. Il loro prodotto non può essere inferiore a una certa costante che contiene nientedimeno che la costante h di Planck, che ormai conosciamo benissimo. Se un errore diventa piccolissimo, l’altro è costretto a crescere di molto.
Lasciamo da parte, per un attimo, il nostro sciame di api che gira attorno al suo alveare e pensiamo a quell’atomo che ci si para d’avanti. Non vediamo un vero e proprio muro e nemmeno un otto volante, però una barriera c’è di certo. Essa è quella che non permette a cariche di segno uguale di andarsene per strade opposte. Le api “positive” che stanno all’interno dell’alveare vorrebbero allontanarsi tra loro, ma l’interazione nucleare forte lo vieta e le costringe a restare in quel "buco" che sembra senza uscita. Analogamente, gli elettroni sotto l’azione dell’interazione elettromagnetica, vorrebbero entrare, attratti dalle api positive, e invece sono tenuti a distanza. Che strano alveare è l’atomo! Le due forze, nucleare forte ed elettromagnetica, sembrano lottare una contro l’altra e creare barriere insuperabili.
Siamo proprio nelle stesse condizione della pallina da tennis che sbatte contro al muro o -ancora meglio- nelle condizione del carrello dell’otto volante che vorrebbe salire fino a C. Per superare una barriera energetica insuperabile è necessaria un’energia che proviene da qualche personaggio da fiaba.
Scavare un tunnel nell’otto volante
Ritorniamo alla Fig. 2 dell’ottovolante e vediamola a livello microscopico. Abbiamo delle particelle che stanno nel buco nei pressi di B e delle altre particelle che, invece, se ne stanno in D. Quelle in B vorrebbero salire fino a C e poi cadere verso D. Quelle in D vorrebbero salire fino in C per scendere in B e, poi, andarsene ognuna lontana dalle altre. La cosa migliore per accontentare entrambi i gruppi di particelle sarebbe quello di scavare un tunnel attraverso la “montagna” che ha come cima C. Forse qualche nostro ex ministro penserebbe anche di riuscirci, attraverso l’incompetenza, ma la MQ lo fa per davvero…
La spiegazione di tutto sta, in pratica, nelle definizione di “particella” che non è né onda né corpuscolo, ma viene ben rappresentata da una funzione d’onda probabilistica, come abbiamo visto, ad esempio, nella QED e nell’introduzione alla MQ, ma anche in tante altre occasioni. Ciò vuol dire che la reale posizione di una particella è legata alla probabilità che essa ha di trovarsi in un certo punto. In parole povere, potremmo dire che la posizione di una particella che sta in uno dei due buchi descritti prima (B e D) può anche avere una possibilità non nulla di trovarsi al di là della montagna. In fondo, anche quella posizione così assurda può avverarsi.
Ciò si può tradurre visivamente nella Fig. 3. La particella descritta dalla sua onda probabilistica si avvicina alla barriera teoricamente impenetrabile. Ebbene se la barriera energetica non è troppo spessa, l’onda riesce a proseguire attraverso di essa, diminuendo la sua ampiezza, e si ritrova, pur estremamente ridotta, al di là del muro. Il fatto che abbia ridotto la sua ampiezza vuol solo dire che è diminuita di molto la probabilità di eseguire questo esercizio, del tutto magico per la nostra vita quotidiana (ricordatevi tutte le somme e moltiplicazioni eseguite nella QED...).
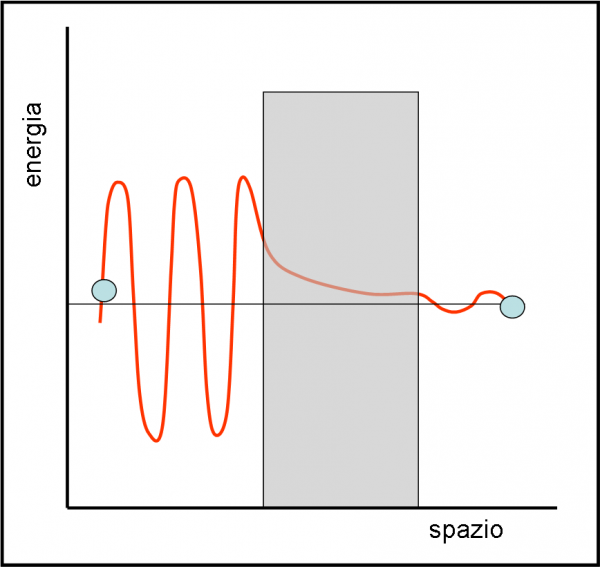
Se non amiamo troppo le onde e le funzioni d’onda, espresse con formule sicuramente non semplici, possiamo spiegare la situazione riprendendo il principio d’indeterminazione. Se conosciamo sempre meglio la posizione di una particella (vicinissima alla parete invalicabile) siamo costretti a non conoscere la sua direzione di movimento o la sua velocità e questa può anche averla portata al di là del muro.
E’ ancora più evidente la soluzione se si considera il principio d’indeterminazione quando coinvolge il tempo e l’energia. La formula è praticamente la stessa:
dE dt > h/4π
Se il tempo si riduce quasi a zero, l’energia può assumete valori del tutto inaspettati anche molto grandi. In particolare, l’energia può superare la barriera che teoricamente non potrebbe superare. Questa situazione è analoga a quella che ci dice che in tempi estremamente corti si può anche creare energia dal nulla. L’importante è che tutto torni alla situazione precedente in una frazione infinitesima di tempo. Se ci pensate bene, questo è quanto abbiamo detto relativamente alla creazione di energia nel vuoto quantico… Ma non allarghiamo tropo il discorso.
Una magia usata tutti i giorni
Sembra di parlare di pura teoria e, invece, le stelle non riuscirebbero a vivere senza questo effetto (loro hanno tanti atomi…). In particolare, non riuscirebbe a superare la forza nucleare forte che tiene unito l’atomo. Senza l’effetto tunnel non ci sarebbe, perciò, decadimento radioattivo, il fenomeno che fa scappare particelle dall’interno del nucleo verso l’esterno… ma non riuscirebbero nemmeno a unire due nuclei atomici e quindi a ottenere la fusione nucleare o la cattura degli elettroni da parte del nucleo. Non ci sarebbero nemmeno i trasporti di elettroni che ci permettono di costruire i microscopi a effetto tunnel e cento altre applicazione che stanno evolvendo dalla tecnologia dei computer fino alla medicina più sofisticata.
Insomma, le stelle e molte altre cose non potrebbero esistere…
Non ho voluto inserire formule (non difficilissime a un primo livello, ma che diventano mostruose se si introduce la funzione d’onda). Tuttavia, con quanto già sappiamo sulla MQ, direi che l’effetto può essere compreso perfettamente a livello concettuale.
Riassumendo:
L'Effetto Tunnel è la capacità che possiedono le particelle quantistiche di attraversare una barriera energetica più alta dell'energia che avrebbero a disposizione!
Non c'è posto per tutti: il PRINCIPIO DI ESCLUSIONE DI PAULI
Per potere descrivere al meglio questo principio sarebbe necessario introdurre e analizzare in dettaglio il Modello Standard, quello che descrive tutte le particelle del microcosmo e le interazioni a cui sono soggette. Un argomento piuttosto complesso e non certo riassumibile in poche parole. Continuiamo a rimandarlo (ma prima o poi ci arriveremo, ve lo prometto!). Tuttavia, è ora di prenderne in prestito una piccola parte e applicarla ai nostri amici più intimi (gli elettroni) che insieme ai fotoni ci hanno permesso di parlare di QED e di tante altre bellissime cose.
In tal modo, anche se in maniera qualitativa, possiamo descrivere il principio di esclusione di Pauli, che insieme al principio di indeterminazione di Heisenberg (prima o poi proseguiremo la nostra analisi pseudo-filosofica), è una delle basi su cui poggia tutta la materia e la Natura. Se Heisenberg può forse dirci il “perché” originale, Pauli riesce molto bene a spiegarci il “come” oltre che i “perché” relativi a oggetti tra i più caratteristici dell’Universo. Possiamo dire che Heisenberg ha dato il via al TUTTO, mentre Pauli si è occupato di sistemare le cose in modo che la materia sopravvivesse e si organizzasse, in condizioni anche estreme. La mente e il braccio?
Iniziamo con un banale esempio della vita di tutti i giorni. Potremmo dire, sbagliando non poco, che il principio di esclusione assomiglia a ciò che capita in una metropolitana all’ora di punta (o in un autobus o in un tram). Le persone cercano di salire in tutti i modi, ma quando non c’è più spazio sono costrette a restare a terra.
No, non è questo il principio di Pauli! Questo è solo e soltanto il principio di incompenetrabilità dei corpi solidi. Più di una persona non può stare in un dato spazio! No, non ci siamo… il principio di Pauli è molto più raffinato e selettivo e lavoro proprio alla base di tutto, a livello atomico. Lui è abituato a ben altre forze e non avrebbe difficoltà a trovare qualche amica capace di spingere ancora di più due persone in un autobus e costringerle a diventare un unico ammasso di carne. Non guardatelo, però, come un brutale assassino… lui è abituato a lavorare con le particelle elementari ed è completamente estraneo ai “fatti di sangue” tanto amati dai media televisivi. La compenetrabilità dei corpi umani è un risvolto trascurabile del lavoro che è costretto a compiere e che mira a oggetti ben più importanti per il Cosmo.
Tanto per anticiparvi un paio di conclusioni pensiamo subito che è proprio grazie a Pauli che esistono le nane bianche e le stelle di neutroni. In questi casi sì che le forze che cercano di fare stare tante persone in un piccolo tram agiscono alla grande e c’è veramente bisogno di un principio della MQ.
Come dicevamo prima, il lavoro del principio di Pauli è molto selettivo e non farebbe mai intasare un autobus, a meno di non essere in condizioni veramente critiche. Lui lavora benissimo e mantiene un ordine perfetto. Se la materia, poi, subisce forze inaspettate e violentissime dà veramente il meglio di sé, a costo di far degenerare la stessa materia pur di farla sopravvivere. Solo i buchi neri sembrano sconfiggerlo, ma nessuno sa veramente cosa avviene all’interno dell’orizzonte degli eventi…
Come fa a non intasare un autobus in condizioni “normali”? Facile. Facciamo un esempio molto banale e semplicistico. Pauli divide le persone secondo quattro caratteristiche. Siano, ad esempio l’altezza, il peso, il colore della pelle (no, non è razzista, anzi… lo fa solo per non creare confusione) e il numero delle scarpe. Lui controlla chi sale e se è già entrato un bianco che pesa 75 kg, è alto 1.70 m, porta il 44, nessun altro con queste caratteristiche può prendere quell’autobus. Voi non ci crederete, ma la selezione funziona molto bene a livello microscopico, con gli spazi che vi sono a disposizione, le caratteristiche degli abitanti, le leggi probabilistiche che li definiscono e i mezzi di … trasporto. Che la cosa funzioni molto bene è sotto gli occhi di tutti: la materia c’è ovunque nell’Universo e se la cava perfettamente!
A questo punto, finiamo di scherzare e andiamo, in silenzio, a vedere cosa succede attorno a un nucleo atomico, facendo particolare attenzione agli elettroni che conosciamo molto bene (ma avremmo anche potuto considerare altre particelle del tipo fermione, ma non quelle del tipo bosone… ci torneremo, state tranquilli).
In una serie di articoli, siamo arrivati a descrivere l’atomo senza entrare prepotentemente al suo interno con la MQ. Non l’abbiamo fatto restando in attesa del Modello Standard. Tuttavia, sappiamo abbastanza bene che gli elettroni hanno a disposizione delle particolari orbite, che possono anche diventare un po’ “strambe” e cambiare orientamento. In realtà, anche senza averne parlato in dettaglio, non è difficile immaginare che queste orbite diventano solo zone probabilistiche (orbitali), regioni in cui un elettrone può esistere ma di cui non è possibile conoscere la vera posizione. Questa parte del lavoro è gestita perfettamente dal principio di indeterminazione di Heisenberg. Che non sia un’orbita ben definita, ma solo onda di probabilità, importa relativamente poco per il nostro scopo. In qualche modo, l’elettrone ha a disposizione un certo spazio in cui muoversi e assistere ai fenomeni della Natura che spesso e volentieri lo coinvolgono.
Anche gli elettroni, come gli uomini, hanno caratteristiche “fisiche” che li distinguono gli uni dagli altri, sia per la posizione che occupano, sia per la loro struttura più intima. Descriviamo queste quattro caratteristiche in modo molto semplificato…
La prima caratteristica è chiamata numero quantico principale n. E’ La parte che meglio conosciamo dato che indica il livello di energia dell'elettrone, ossia corrisponde sostanzialmente a una delle orbite stazionarie individuate da Bohr (ricordate la storia dell’atomo?). Esso assume valori interi e positivi.
La seconda è il numero quantico secondario . Esso indica i vari tipi di orbita che ci possono essere in ogni livello energetico, e può assumere tutti i valori da 0 a n-1. Ogni orbita ha un suo valore energetico particolare (possiamo chiamarlo sottolivello). In tal modo per un certo numero principale esistono altrettanti sottolivelli. In altre parole, a ogni sottolivello corrisponde una ben precisa forma dell'orbita degli elettroni che ne fanno parte, che diventa sempre più complicata al crescere del numero secondario, secondo quanto descritto matematicamente dalla famosa funzione d’onda di Schrodinger (quello dell’altrettanto celebre gatto). Questi due numeri quantici definiscono in qualche modo l’energia dell’elettrone (il suo peso e la sua altezza?).
Non è finita, però: esiste anche un numero quantico magnetico. Qui si va veramente nel sottile… Abbiamo visto che ogni sottolivello ha una sua orbita. Tuttavia, questa orbita può assumere orientazioni diverse. Il numero quantico magnetico indica il numero di orbite che possono coesistere in un determinato sottolivello. Queste orbite (sarebbe meglio chiamarle “orbitali”) hanno, quindi la stessa forma e la stessa energia, ma sono orientate in modo diverso.
Il numero magnetico ci permette di stabilire quanti elettroni possono esistere in un certo sottolivello. Sommando gli elettroni di tutti i sottolivelli si determina il numero possibile di elettroni che possono esistere nel livello energetico preso in considerazione.
Finora abbiamo parlato di posizioni ammissibili in un intricato gioco di orbite (o di orbitali) che meglio indicano la sostanza probabilistica di esse. Teniamo sempre presente che per l’elettrone determinare una posizione equivale a determinare la probabilità di trovarsi in dato intervallo ristretto definito dalla MQ.
E’ giunta l’ora di considerare anche la parte più intima dell’elettrone (il colore della pelle?). L’altezza e il peso potevano essere comuni a vari colori, ma il colore della pelle è una caratteristica intrinseca, che non dipende più dall’energia legata al livello, al sottolivello e all’orientamento (un nero e un bianco possono avere la stessa posizione, la stessa altezza, lo stesso peso, lo stesso numero di scarpa, ecc.).
Fortunatamente, gli elettroni possono solo essere o bianchi o neri. In realtà, è molto meglio dire che possono “girare” solo in due modi. Sappiamo che gli elettroni rivolvono attorno al nucleo atomico di cui fanno parte, ma sono anche capaci di ruotare attorno a un asse (non è una vera rotazione fisica, ma ideale… ci torneremo sopra a tempo debito). Questa caratteristica regala il quarto parametro all’elettrone, il numero quantico di spin (in inglese “spin” significa proprio rotazione). In modo del tutto arbitrario è stato assegnato un valore di +1/2 e -1/2 a chi “gira” in senso orario e antiorario, rispettivamente.
Abbiamo finalmente definito le quattro caratteristiche, ossia i quattro numeri, che identificano perfettamente un elettrone e la sua energia. Abbiamo definito l’altezza, il peso, il numero delle scarpe e il colore della pelle. In parole più tecniche, il suo stato quantico.
A questo punto entra in scena il principio di esclusione di Pauli che dice categoricamente: “In un atomo non possono mai trovarsi due elettroni aventi gli stessi quattro numeri quantici (ossia lo stesso stato quantico)”.
Una selezione che risulta più che efficiente in Natura. Se non esistesse questo principio ci potrebbe essere una sovrapposizione di elettroni nello stesso orbitale (ossia con gli stessi primi tre numeri quantici). Il quarto parametro ammette invece solo due elettroni con numero di spin opposto. Tutti gli altri devono restare a terra (o -meglio- devono usare un altro autobus)!
I numeri quantici possono anche essere visti secondo termini più comprensibili, tenendo conto che maggiore distanza dal nucleo vuol dire diversa energia e, di conseguenza, diversa velocità e massa relativistica (che dipende proprio dalla velocità). I numeri quantici possono anche essere tradotti in: massa, velocità, spin, posizione
Ribadiamo ancora il concetto. Se non ci fosse il principio di esclusione, gli elettroni si accumulerebbero sull’orbitale a energia più bassa, quello che prediligono per … natura. Esso è molto vicino al nucleo e per gli atomi più pesanti è proprio quasi a contatto. Normalmente la materia non necessita un particolare intervento: gli autobus viaggiano abbastanza vuoti.
Il problema nasce quando troppi elettroni cercano di inserirsi nelle orbite più basse (dove la loro velocità è anche la più bassa). Ecco allora che il principio di Pauli diventa importantissimo.
Immaginiamo che la gravità diventi così forte che le reazioni nucleari del nucleo non riescano più a fronteggiarla. Arrivano elettroni “liberi” da tutte le parti, cercando rifugio negli orbitali meno energetici degli atomi. Tuttavia, Pauli dirige il traffico e non ammette una folla disordinata che farebbe collassare il tutto. Gli elettroni che cercano riparo nell’orbitale più basso vengono ricacciati verso orbite più alte acquistando velocità. La materia diventa in qualche modo degenere, ma riesce, attraverso le velocità degli elettroni cacciati dalle zone già occupate, a ribellarsi alla forza gravitazionale. La stella blocca il suo collasso e siamo nel caso della nana bianca.
Notiamo che aleggia sempre su tutto il principio di Heisenberg: due elettroni troppo vicini tra loro consentirebbero una precisione troppo alta alla loro posizione ed è necessario che compaia una grande variabilità nella loro velocità. Il principio di Pauli segue questo indirizzo: gli elettroni con lo stesso numero di spin devono distinguersi per la loro velocità, cioè non possono muoversi allo stesso modo e devono cambiare livello. In altre parole, più elettroni sono compresi in un piccolo spazio, più devono essere quelli con velocità maggiori. Queste velocità danno origine a una pressione che si oppone a ogni tentativo di comprimerli ulteriormente. Il risultato pratico del principio di esclusione di Pauli è che ogni piccolo volume di spazio può contenere soltanto un certo numero di particelle che si muovono a una particolare velocità; si possono aggiungere particelle, ma solo aumentando le loro velocità.
Ciò che si ottiene è una nube di elettroni che cercano di rimanere ancorati ai nuclei atomici rivolvendo a velocità molto elevate: una specie di folla di naufraghi che cerca di non allontanarsi dalla nave che ancora galleggia. Una folla in preda alla paura che il principio di Pauli riesce a gestire, pur accettando una struttura degenere della materia. Tuttavia, più di tanti elettroni naufraghi non si riescono a sistemare attorno a un nucleo.
Riassumiamo il concetto astrofisico: La stella collassa per auto gravitazione a causa dell’esaurimento delle reazioni nucleari. La densità centrale sale e molti elettroni vengono a trovarsi nella stessa posizione quantistica definita dal principio di Heisenberg. Tanto maggiore è il numero di elettroni che si vanno ad aggiungere, tanto più alti sono i valori di velocità che "gli ultimi arrivati" devono acquisire, dal momento che i valori più bassi sono già stati “utilizzati” dagli elettroni che si sono addensati in precedenza: il principio di Pauli non ammette più di due elettroni (con spin opposto). Un gioco perfettamente combinato dei due principi: il primo definisce quando la “posizione” quantica può essere considerata “uguale”, il secondo elimina quelli che ce l’hanno e cercano di convivere in numero maggiore di due.
E' facile capire che la pressione del gas di elettroni cresce al crescere della velocità con cui tali elettroni vengono “scartati” dal principio di Pauli, ovvero all’aumentare della loro densità. Quando la densità sale sufficientemente, la pressione elettronica è in grado di contrastare la gravità e la stella si assesta diventando una nana bianca.
Vale la pena notare una conseguenza molto importante della pressione quantistica. Essa non è legata in alcun modo alla temperatura della stella degenere, dato che gli elettroni aumentano la loro energia cinetica solo perché ESCLUSI dalle zone già occupate. Le nane bianche, perciò, restano in equilibrio senza bisogno di fusione nucleare o di altri strani effetti termici. Possono raffreddarsi tranquillamente dato che la pressione in grado di fronteggiare la gravità dipende solo da questioni di… sovrabbondanza.
Se, però, la massa della stella supera le famose 1.4 masse solari (massa di Chandrasekhar), la pressione derivata dal principio di Pauli, agente sugli elettroni, non è più sufficiente a fermare il collasso. In particolare, la velocità degli elettroni è ormai del tutto paragonabile a quella della luce. Essi, allora, urtano senza alcun ritegno i protoni del nucleo, alla faccia delle regole “normali”. Elettrone più protone vuol dire neutrone. La stella si trasforma da un mare di elettroni in un mare di neutroni, per i quali, però, vale ancora il principio di Pauli che vieta una posizione troppo vicina ai protoni. La pressione dei neutroni “scacciati” diventa così alta da pareggiare nuovamente la gravità. La densità è ora almeno cento milioni di volte più alta di quella di una nana bianca e la stella si trasforma in stella di neutroni, ritrovando l’equilibrio con un diametro di pochi chilometri.
Se, infine, la massa supera le tre masse solari, nemmeno la pressione dei neutroni riesce a bilanciare il collasso gravitazionale e la materia non segue più le regole conosciute. Cosa diventa? Mi spiace… dovete andarlo a chiedere direttamente a un buco nero, sempre che lui vi faccia entrare e -soprattutto- uscire!
QUI una semplice storia della Meccanica Quantistica raccontata da Einstein e Bohr, attraverso le interazioni umane e professionali di alcuni dei grandi scienziati che l'hanno fatta nascere e crescere.
QUI la dualità onda-particella spiegata dal nostro amico Curiuss grazie ad un ornitorinco e un'attrice svizzera



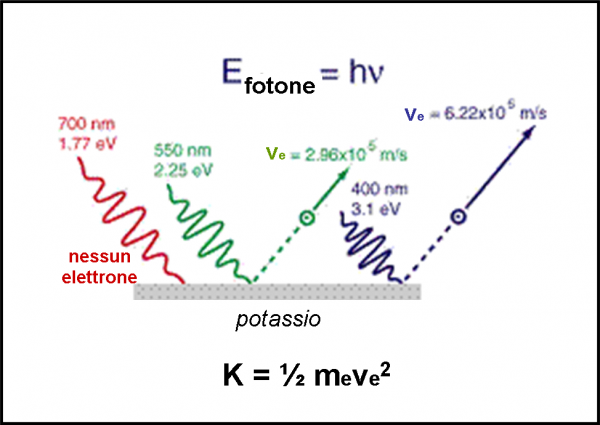




24 commenti
Quando fai così Enzo, ho una sola parola:
MAGNIFICO!
Sarebbe da stampare, metterselo sotto un braccio ed andarsene in un romitorio a gustarselo in santa pace, parola per parola!
adulatore!!!!!



E NO!!!
Dalle mie parti si dice così: quanno ce vò ce vò!!!! Ecchè piffero ....
Non ho ancora letto l'articolo, ma sono d'accordo con Alvy!!!
no, non aspettatevi niente di nuovo... ho solo messo insieme gli articoli pubblicati in tempi diversi. Niente di speciale!
A te, Prof., può sembrare poco ma per noi comuni mortali è di fondamentale importanza... spesso la difficoltà maggiore (specialmente per gli studenti) non è capire singoli argomenti ma collegare il tutto in una visione d'insieme


grazie Daniela, se può anche minimamente aiutare qualcuno ne sono ultrafelice e continuerò a seguire questa strada di riassunti legati assieme...
...e io sono strafelice di questa tua decisione


caro enzo, sei instancabile...peccato per il poco tempo a mia disposizione causa lavoro perchè mi piacerebbe cimentarmi con i tuoi quiz.
comunque le nozioni teoriche riesco a studiarle nell'attesa ai dottori che devo andare a vedere ogni giorno.
I miei complimenti per due cose che ritengo molto importanti, e che legate insieme danno un bell'impulso alla tanto necessaria diffusione della cultura scientifica. Ovvero: la capacità di comunicare, e il desiderio di comunicare le proprie esperienze e conoscenze.
Continui così, per favore...
Alberto
grazie Alberto
Finché ci sono persone come voi non mollerò di certo (età permettendo...)!
E nel viaggio di ritorno mi sono sparato pure questo...grande Enzo, riassuntone spettacolare come al solito.
Un cosa, quando dici "La stella si trasforma da un mare di elettroni in un mare di neutroni, per i quali, però, vale ancora il principio di Pauli che vieta una posizione troppo vicina ai protoni"....vuol dire che nelle stelle neutroniche ci sono ancora protoni?
A costo di rischiare una figuraccia, provo a rispondere io, chiedendo scusa a tutti (in particolare al Prof.) per il linguaggio probabilmente poco tecnico...
Durante l'esplosione della supernova che dà origine alla stella di neutroni, l'enorme energia fa letteralmente schizzare via gli elettroni da ogni atomo e si "compattano" i nuclei, che sono costituiti da neutroni e protoni.
Considerando che ogni atomo è principalmente costituito da spazio vuoto (se il nucleo fosse grande come una capocchia di spillo, gli elettroni ruoterebbero intorno descrivendo una sfera con raggio di circa 200 metri) e che la quasi totalità della massa è concentrata nel nucleo, il risultato è una stella piccolissima con una densità altissima.
Grazie Daniela, ma il punto che intendevo io era un altro. Oltre il limite di Chandrasekhar la pressione diventa così elevata che gli elettroni cominciano a combinarsi con i protoni dando origine a neutroni liberi...a questo punto, una volta passati dallo stato di nana bianca a quello di stella neutronica, ero convinto che la stella fosse composta solamente da neutroni, ma Enzo scrive "La stella si trasforma da un mare di elettroni in un mare di neutroni, per i quali, però, vale ancora il principio di Pauli che vieta una posizione troppo vicina ai PROTONI"...volevo capire come potessero esistere ancora protoni all'interno di un mare degenere di neutroni.
Giusto... quindi è meglio che ti risponda il Prof.
cari Dany e Lampo,
il passaggio da atomi a neutroni (e basta)è graduale all'interno della stella e viaggia in accordo con la pressione da contrastare. Diciamo che prima che i neutroni rimangano da soli (sempre che ci riescano completamente) il principio di Pauli compie un ottimo lavoro. Dopo chissà cosa interviene esattamente. Ricordiamoci che si sa ancora ben poco della materia che compone le stelle di neutroni e soprattutto del loro nucleo più interno.
Buongiorno Prof
se mettessimo un rilevatore "intelligente" in corrispondenza del foro che ci dice avvisa del passaggio dell'elettrone o fotone, dunque ci dice che è passato e il momento esatto in cui è passato, l' effetto di diffrazione comunque?
grazie
Il principio di Heisenberg la vuole comunque: se conosci la posizione non conosci la velocità e viceversa. Un tempo da solo non permette di ricavare la velocità. Ce ne vogliono due, ma allora salta la posizione...
Chiaro grazie.
Approfitto per un ulteriore chiarimento su questo aspetto. Nell' esperimento della doppia fenditura si dice che rilevare il fotone al passaggio da una delle due fenditure determina il collasso della funzione d onda e dunque la perdita del fenomeno di interferenza.
Analogamente,immagino, possiamo dire che il passaggio da singola fenditura ( perlopiù "intelligente") determina il collasso della funzione di onda del fotone . Dopo la fenditura però il fotone riacquista nuovamente una natura ondulatoria che determina il fenomeno della diffrazione. Significa che il collasso può essere momentaneo eil fotone,fino a che non viene fermato, può proseguire la sua corsa riprendendo natura ondulatoria?
Grazie ancora
Pardon mi sono accorto di aver inviato il commento usando l account di posta preimpostato del mio coinquilino Franco (entrambi siamo lettori appassionati dei suoi articoli), ma sono sempre Michele
caro Michele/Franco (siete anche voi un po' quantistici?),
direi proprio di sì e tutto si basa sul principio di Heisenberg, dato che abbiamo rivelato il fotone, ma non sappiamo assolutamente dove vada... Diciamo, in parole povere, che è stata eliminata l'onda dell'altra fenditura interferenza), ma il fotone può ancora decidere dove andare su base probabilistica.
Buongiorno Prof rimando commento del 3 giugno nel caso non fosse arrivato.
Chiaro grazie.
Approfitto per un ulteriore chiarimento su questo aspetto. Nell' esperimento della doppia fenditura si dice che rilevare il fotone al passaggio da una delle due fenditure determina il collasso della funzione d onda e dunque la perdita del fenomeno di interferenza.
Analogamente,immagino, possiamo dire che il passaggio da singola fenditura ( perlopiù "intelligente") determina il collasso della funzione di onda del fotone . Dopo la fenditura però il fotone riacquista nuovamente una natura ondulatoria che determina il fenomeno della diffrazione. Significa che il collasso può essere momentaneo eil fotone,fino a che non viene fermato, può proseguire la sua corsa riprendendo natura ondulatoria?
Grazie ancora
Scusi ho fatto con confusione non avevo visto la sua risposta del 4 giugno!
Grazie e saluti quantici da Michele e Franco
di niente... grazie a te Franmichele!!!!