Questo articolo è stato inserito nelle sezioni d'archivio Dinamica e Meccanica e in Meccanica Celeste

 

15/10/2014

In questo articolo ripropongo quanto avevo scritto tempo fa sull’effetto fionda. Tuttavia, per chi volesse capire che, in fondo, la fisica utilizza sempre le stesse leggi fondamentali, ho aggiunto un pezzo in più che ci ricollega perfettamente alla MQ e all’effetto Compton, all’esperienza di Rutherford e alle sue particelle che tornano indietro. Per non dire della riflessione descritta dalla QED. Un tentativo per generalizzare il più possibile e guardare a 360°. Ormai siete (anzi siamo) tutti cresciuti!

Inizio riportando l’articolo già pubblicato introducendo pochissimi cambiamenti. Non vi sono formule e l’effetto fionda dovrebbe essere spiegato in modo più che comprensibile, compresi i suoi collegamenti con la conservazione dell’energia. Il finale ci porta anche verso un urto frontale ed è proprio a quel punto che ho inserito la parte nuova, con qualche formula, ma soprattutto con concetti che si alzano “in volo” per mostrarci la fisica in un contesto ben più generale...

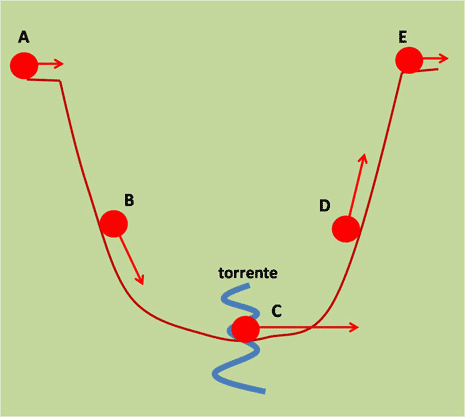
Immaginiamo di essere ciclisti molto temerari (ad esempio assi della mountain bike) e buttiamoci lungo un percorso tortuoso e insidioso. A un certo punto ci troviamo di fronte a una discesa terribile seguita da un altrettanto ripida salita. Ad esempio, una piccola valle percorsa da un torrente, attraversato da un piccolo ma sicuro ponte. Noi non abbiamo paura e ci lanciamo verso il basso acquistando velocità. Sul ponte arriviamo come dei razzi e proseguiamo anche in salita, sfruttando la velocità guadagnata in discesa, fino a raggiungere il bordo opposto della valle (senza toccare i pedali) e proseguire la corsa. In queste condizioni, abbiamo guadagnato velocità e poi l’abbiamo persa, ma, alla fine, (immaginando che non ci siano stati attriti: il sentiero è liscio come un biliardo) siamo tornati a quella che avevamo prima di scendere (magari proprio zero, dato che prima di buttarci giù ci siamo fermati).

E’ la stessa cosa che capita sulle montagne russe del Luna Park: si sale in alto, si scende a perdifiato e si ritorna in alto senza bisogno di alcun motore. Ovviamente è vietato assolutamente usare i freni! Si sfrutta soltanto l’energia potenziale, ossia quella che dipende dalla gravità (in questi casi quella della Terra, che ci aiuta a scendere verso il basso). In altre parole: si deve conservare l’energia totale del sistema. L’energia totale è data da quella potenziale (dovuta alla gravità) e da quella cinetica (dovuta alla pedalata precedente). Quando scendiamo verso il torrente perdiamo in energia potenziale (veniamo attratti verso il basso dalla gravità terrestre) e guadagniamo in energia cinetica (acceleriamo nella discesa). Arrivati in fondo l’energia potenziale è minima (non possiamo più scendere), ma abbiamo raggiunto il massimo di energia cinetica. Questa ci permette di proseguire in salita, ma, ovviamente, riguadagniamo in energia potenziale e cominciamo a perdere in energia cinetica (rallentiamo).

Se non ci sono attriti, riusciamo ad arrivare in cima, con la velocità che avevamo prima di scendere. La Fig.1 illustra la situazione, mettendo al posto della bicicletta una pallina.

Voi mi direte: “E allora? Che c’entra con una sonda, Giove o un altro pianeta?”.  Eppure la situazione è “quasi” identica.

Immaginiamo che Giove sia fermo nello spazio, senza girare attorno al Sole  e consideriamo la nostra navicella che sta arrivando verso di lui con una certa velocità v. Tutto è identico a quanto capitava a noi quando stavamo pedalando. Se le condizioni sono quelle giuste (distanza sufficiente da Giove e velocità abbastanza elevata; come dire se siamo bravi ad andare in bicicletta e non usiamo i freni) siamo attratti da Giove che ci fa girare attorno a lui, perdendo in energia potenziale e guadagnando in energia cinetica. Al “giro di boa” abbiamo la massima velocità. Poi proseguiamo in verso opposto (come prima continuavamo in salita) perdendo velocità e guadagnando in energia potenziale. Alla fine siamo tornati alla stessa velocità che avevamo prima dell’incontro, avendo però cambiato completamente direzione (Fig. 2a).

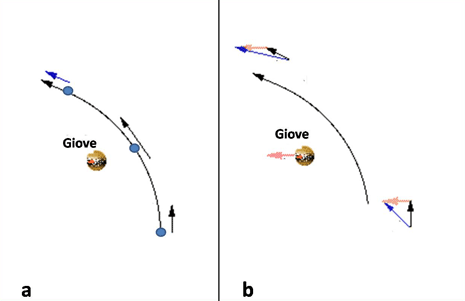
Mi direte: “Sì, molto bello, ma non è che ci guadagniamo molto. Per cambiare rotta forse si poteva fare in altro modo …”. A questo punto, allora, facciamo muovere Giove lungo la sua orbita. Adesso sì che le cose cambiano. D’altra parte a noi interessa acquistare velocità NON rispetto a Giove, ma rispetto al Sole, se vogliamo, ad esempio, raggiungere Plutone e la Kuiper Belt. Quindi ci poniamo in un sistema di riferimento diverso, in cui Giove si muova davvero.

Allora, consideriamo la stessa figura di prima, ma facciamo viaggiare Giove con una velocità V. Dopo il giro di boa la velocità della navicella deve tenere conto che Giove sta andando proprio dalla sua parte e allora per conservare l’energia del sistema, ossia poter proseguire abbandonando Giove, deve andare a una velocità maggiore di quella che aveva prima di raggiungere Giove. Se la velocità era v, si arriva a valori più alti avvicinandosi a Giove (dobbiamo “combinare” le due velocità con la ben nota “somma vettoriale”) e poi si prosegue fino a raggiungere il valore massimo in uscita dal passaggio ravvicinato (Fig. 2b). In condizioni limite si può arrivare a guadagnare il doppio della velocità orbitale di Giove, che è di circa 13 km/sec. Sempre tutto in accordo con la conservazione dell’energia totale.

Volete un altro esempio (sperando che non vi confonda le idee …)? Immaginiamo di essere in una stazione e voler lanciare una pallina da tennis contro un treno che arriva in senso opposto e che non si ferma. Se lancio la pallina a 50 km/h e il treno viaggia a 100 km/h, a che velocità avverrà l’urto? Presto detto: 100 + 50 = 150 km/h. Infatti, se avete uno scontro contro un muro o contro una macchina che viene in senso opposto a voi, le conseguenze sono ben diverse. Per calcolare la velocità d’impatto, le due velocità si devono sommare.

A questo punto la palla deve rimbalzare in senso opposto con la stessa velocità, ossia 150 km/h. Ma il treno deve vedersela scappare davanti e quindi la pallina rimbalza a una velocità di 150 km/h (come era arrivata) più i 100 km/h del treno. Infatti il treno ha trasferito alla pallina la sua velocità. La pallina schizza a 250 km/h. Questo ovviamente in condizioni perfette e senza attrito.

La Fig.3 mostra una vignetta che riporta questa situazione con valori diversi (miglia per ora), ma il concetto è lo stesso. Anche in questo caso siamo riusciti a lanciare una palla a 30 miglia/ora e a farla rimbalzare a 30 + 2×50 = 130 miglia/ora, come nel caso di Giove. Se il treno fosse stato fermo, la pallina sarebbe rimbalzata alla stessa velocità del lancio, ossia 30 miglia/ora. E’ quindi fondamentale che l’oggetto che ci deve dare l’effetto fionda sia in movimento. In realtà, l’effetto fionda prende anche il nome di “rimbalzo elastico”, proprio per come le due situazioni si assomigliano. La velocità del treno (o meglio la sua energia cinetica) prende il posto della gravità di un pianeta. Il Sole, ovviamente, sta a guardare (siamo nel suo sistema di riferimento)!

QUI approfondiamo la spiegazione del motivo per cui la velocità del treno compare due volte nel calcolo della velocità acquisita dalla pallina

 

Urtiamoci senza toccarci

Allacciamoci proprio alle ultime frasi. La fionda gravitazionale non è altro che un urto elastico perfetto. Perché perfetto? Perché nei casi in cui due palline, come quelle del biliardo, si urtano vi è sempre una dispersione di energia (attrito o compressione della massa o molte altre cose) e le condizioni non sono quelle ideali. Per ottenere un urto perfetto bisognerebbe che le due palline che si urtano non si tocchino assolutamente! Ma com’è possibile?

Presto detto. Quando vi è un urto, vi è uno scambio di favori tra le due palline: la prima esercita una forza sulla seconda e la seconda l’esercita sulla prima. Tuttavia, il terzo principio della dinamica ci dice che le due forze devono essere uguali e contrarie, ossia la forza totale esterna agente sulle due palline deve essere nulla. In tali condizioni si conserva il momento della quantità di moto. Questa parte l’ho spiegata molto bene (penso) nella “Fisica addormentata nel Bosco”… e ci torneremo parlando di momento angolare.

In ogni modo, il concetto è molto semplice e possiamo considerarlo come uno scambio di favori eseguito in modo che il sistema formato dalle due palline mantenga inalterata la sua capacità di movimento TOTALE, sia prima che dopo l’urto. Al limite ciò che faceva prima una delle due, verrà fatto dalla seconda dopo l’urto.

Come dicevo, però, un urto del genere comporta gravi problemi nella realtà e non è mai perfettamente elastico. Di chi è la colpa? Della forza che agisce tra le due palline. Una forza che ha bisogno del contatto tra le due sfere. Ma, per quale motivo dobbiamo proprio usare una forza che porti a un contatto? Ne conosciamo almeno due che trasmettono ordini senza bisogno di alcun contatto.

La più famosa è la forza di gravità. Un oggetto che abbia una certa velocità può tranquillamente subire (e agire con) una forza a distanza e non avere alcun contatto durante l’azione.

Consideriamo, nuovamente, la nostra pallina che sta per sbattere contro un’altra pallina. Esse si scambiano la forza di gravità: tanto ne do a te e tanta ne dai a me. Non compare nessuna forza esterna al sistema (una è uguale all’altra, di verso opposto e si annullano), ma ciononostante, attraverso di essa, la pallina più piccola percorre una traiettoria attorno alla più grande e poi se ne va per la sua strada. Il tutto è esattamente simile a un urto, in cui, però, non vi è contatto alcuno: un urto veramente elastico!

Cercate di vedere l’arrivo di una navicella verso Giove (ad esempio) come una pallina che “impatta” contro la gravità di Giove e torna indietro da dove era venuta sotto la ferrea regola della conservazione del momento della quantità di moto! Usiamo la semplicissima Fig. 4, che rappresenta il caso limite, ma, se considerassimo traiettorie oblique, la situazione non cambierebbe per niente, a parte introdurre un bel po’ di componenti di vettori e di trigonometria (ricordate le componenti attraverso i versori? Beh… qui si potrebbero usare benissimo per risolvere il problema generale).

A questo punto non ci basta più spiegare il processo “urto senza contatto” solo con le velocità e tante belle parole come nel vecchio articolo. No, vogliamo proprio risolvere il problema in modo fisico. Quali sono i dati del problema? Una navicella di massa m viaggia con una certa velocità v1 verso un corpo di massa M che viaggia con velocità V1. Subiscono l’urto “gravitazionale” e alla fine abbiamo la sonda di massa m che viaggia a velocità v2 e il corpo celeste di massa M che viaggia a velocità V2. Essendoci messi nelle condizioni più semplici della Fig. 4, la direzione di tutte le velocità è la stessa e posso tranquillamente lavorare solo con i moduli, lasciando perdere i vettori (come già detto, se non fosse così dovrei usare grandezze vettoriali e le loro componenti scalari… vedi articolo sul momento angolare).

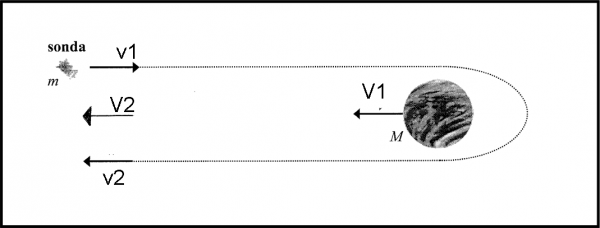
Ovviamente conosciamo le masse, conosciamo la velocità della sonda v1 e quella del corpo V1, ma non conosciamo la velocità finale v2 e nemmeno quella V2. Non basta più imporre la conservazione della quantità di moto del sistema, dato che in una sola equazione abbiamo due incognite. Essa dice:

mv1 + MV1 = mv2 + MV2    …. (1)

Fortunatamente, possiamo anche imporre la conservazione dell’energia del sistema. Ovviamente, l’energia potenziale dovuta alla gravità non interessa dato che agisce durante il passaggio ravvicinato, ma poi “sparisce”, per definizione, dato che la forza mutua che agisce lo fa solo nel momento del “contatto” gravitazionale. Prima e dopo, l’energia potenziale non cambia assolutamente e quindi ci basta conservare l’energia cinetica del sistema (la sonda e il pianeta si muovono e come!). Questa relazione si scrive:

½mv1² + ½ MV1² = ½ mv2² + ½ MV2²     …. (2)

Perfetto, adesso abbiamo due equazioni con le stesse due incognite e il sistema si può risolvere senza problemi.

Come vedete benissimo, ho tenuto in conto della reciproca forza di gravità e non ho certo posto la velocità del pianeta sempre uguale a se stessa oppure uguale a zero. Al limite, potremo ragionarci sopra alla fine.

Molti di voi sono abbastanza preparati e vogliosi di riflessione per capire tutto il discorso che sto facendo. Non è tanto per il risultato finale (ci bastava la trattazione divulgativa e discorsiva), ma per dimostrare come la fisica abbia sempre bisogno di regole precise per risolvere le problematiche. Quando esse non esistono è facile che avvengano anche le … catastrofi… ultraviolette. Inoltre volevo farvi vedere come poche leggi funzionano per tante situazioni che sembrano completamente diverse. La stessa descrizione di un urto senza contatto non l’abbiamo forse vista nell’atomo di Rutherford? Lì, invece della forza di gravità, agiva la forza elettromagnetica e le particelle cariche. Ma non è anche una cosa analoga lo scattering che ci ha insegnato la QED? Anche lì gli elettroni rimbalzavano  uno rispetto all’altro a causa dei fotoni che li mantenevano a distanza o che li facevano rivolvere attorno ai nuclei positivi. Se riflettete ancora più a fondo, il principio di indeterminazione e/o di esclusione sono sempre latenti in questi urti senza contatto… Ma non esageriamo…

Torniamo al nostro effetto fionda trattato in modo correttamente fisico. Forse non ve ne siete ancora accorti, ma la soluzione del sistema (1) e (2) l’abbiamo già trovata in un altro articolo. Un articolo che era cominciato proprio con il biliardo… Sì, proprio quello sull’effetto Compton, un caposaldo della MQ. Che meraviglia! La MQ prende in prestito le stesse identiche formule dell’effetto fionda e ci regala una soluzione che sta poi solo a noi saper interpretare nel modo che c’interessa. Andate a rileggervi quell’articolo, ma, per aiutarvi a seguire il discorso, riporto le formule  che ci danno le velocità finali della sonda e del pianeta (in quel caso due palline). Inseriamo anche le nuove notazioni, al posto di quelle usate nell’effetto Compton, ossia:

v1 = v1

v2 = v1’

V1 = v2

V2 = v2’

m = m1

M = m2

Le relazioni  diventano:

v2 = v1(m – M)/(m + M) + 2MV1/(M + m)    …. (3)

V2 = V1(M – m)/(m +M) + 2v1m/(m + M)   …. (4)

Adesso, possiamo ragionare finalmente sulle possibilità di approssimazione…

M è decisamente più grande di m, per cui sommare o togliere m a M non cambia praticamente niente (attenzione: lo posso fare solo adesso!).

La (3) diventa:

v2 = - v1 M/M + 2V1M/M = - v1 + 2V1    …. (5)

Accidenti… è proprio quello che cercavamo! La velocità finale è uguale a quella di arrivo (cambiata di segno, ossia di verso opposto) a cui viene aggiunto il doppio della velocità iniziale del pianeta. Entrambe queste velocità hanno lo stesso verso e quindi si sommano.

Tuttavia, usiamo anche la (4) dopo aver usato la stessa approssimazione di prima:

V2 = V1M/M + 2v1m/M    …. (6)

Ma m/M è molto piccolo, dato che  M è decisamente enorme rispetto a m e quindi

m/M << 1 (potrei anche dire che tende a zero…).

Risulta:

V2 = V1 + qualcosa che è estremamente piccolo, circa zero.

Insomma, la velocità del pianeta può essere considerata praticamente costante. In realtà, dato che v1 va in verso opposto a quello di V1, la V2 è leggermente più bassa di quella iniziale… Ma stiamo tranquilli: qualsiasi sonda, asteroide, cometa o meteoroide che passi vicino a Giove ha un effetto del tutto trascurabile sul moto del nostro gigante.

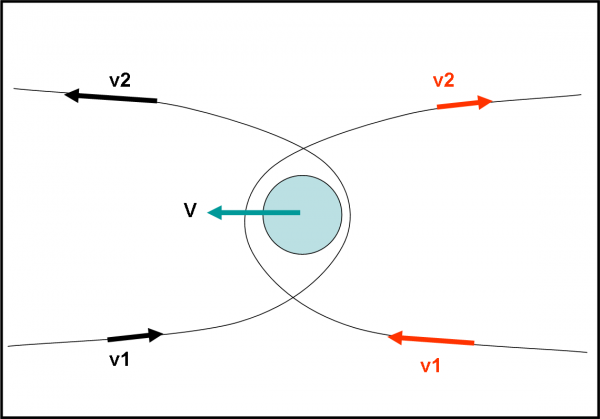
Volendo fare i raffinati, potremmo anche utilizzare l’effetto fionda al contrario. Basta immaginare la nostra navicella che arriva vicino a Giove in modo troppo rapido e vorremmo frenarla. Niente di più facile (normalmente si usano i satelliti del gigante per correggere in modo “raffinato”).  La sonda, questa volta, arriva in verso uguale a quello del moto del corpo celeste. La (5) ci dice allora che la velocità finale cambia di verso (ossia torna da dove è venuta), ma è aggiunta comunque al  doppio della velocità del corpo celeste che va, però, in verso opposto. Insomma, la conclusione è che vi è una differenza di velocità e quindi un rallentamento della sonda.

Il riassunto dei due casi è riportato in Fig.5.

Beh… magari non è stato molto banale, ma tenete ben presenti questo articolo e quello sull’effetto Compton, dato che queste chiacchiere torneranno molto utili col momento angolare. Anzi, potremo anche risolvere il caso generale dell’effetto fionda, con l’arrivo e la partenza della navicella lungo traiettorie inclinate.