Categorie: Matematica
Tags: funzioni semplici integrali indefiniti
Scritto da: Vincenzo Zappalà
Commenti:9
49. Integrali indefiniti di funzioni semplici **
Così come avevamo creato una tabella per riassumere le derivate delle funzioni più comuni, così possiamo facilmente fare lo stesso con gli integrali corrispondenti. Se si vuole integrare una funzione f(x), che sappiamo immediatamente essere una derivata di una certa altra funzione F(x), possiamo identificare l’integrale con quest’ultima funzione. Ma, non sempre, le cose sono così semplici.
Ripetiamo quanto detto un paio di lezioni fa:
Data una funzione f(x), di cui vogliamo calcolare l’integrale indefinito, si deve cercare un’altra funzione F(x), chiamata PRIMITIVA, di cui f(x) sia la derivata.
Ossia:
f(x) = F ’(x).
Abbiamo già introdotto alcuni esempi, ma è bene seguire uno schema più rigoroso. Cerchiamo di ricavare, perciò, gli integrali più semplici e immediati utilizzando, per quanto possibile, le derivate più comuni. Ci accorgeremo che la faccenda è ben più complicata di quanto si possa immaginare…
Come fatto per le derivate, potremmo creare una tabella, calcolando gli integrali delle funzioni più comuni. Facile a dirsi, ma molto meno facile a farsi!
Andiamo per ordine.
Iniziamo con la funzione
f(x) = xn
e vogliamo determinare la funzione:
∫ f(x) = ∫ xndx
Ossia, vogliamo calcolarne l’integrale indefinito. Attenzione a quello che cerchiamo di fare: non vogliamo invertire tutte le derivate che conosciamo (sarebbe troppo comodo), ma vogliamo trovare l’integrale di funzioni semplici e comuni, così come avevamo fatto per le derivate. Pensateci bene, perché non è la stessa cosa…
Utilizziamo la derivata della potenza di x e vediamo di invertire l’operazione.
La derivata di una potenza ennesima di x è data da:
f ’(x) = n x(n-1)
Sarebbe immediato, per definizione di integrale, scrivere:
F(x) = ∫ f ’(x)dx = ∫ n x(n-1)dx = xn
Tuttavia, non avremmo risolto il nostro problema, dato che noi non vogliamo cercare una primitiva che sia una potenza di x, ma vogliamo trovare una primitiva che abbia come derivata proprio la potenza di x. Scusate la ripetizione, ma è importante capire bene il concetto di quello che stiamo per fare
Prima di proseguire è bene ricordare le più semplici proprietà degli integrali indefiniti:
∫ f(x) + g(x) = ∫ f(x) + ∫ g(x)
∫ k f(x) = k ∫ f(x) con k costante
Utilizziamo la seconda e scriviamo:
∫ n x(n-1)dx = n ∫x(n-1)dx = xn
O, ancora:
∫ x(n-1)dx = xn /n
Ci siamo quasi… Basta, infatti, considerare un certo esponente m = n - 1, per ottenere:
∫ xmdx = x(m +1)/(m+1)
Ma m è un numero qualsiasi e quindi è come scrivere:
∫ xndx = x(n +1)/(n+1) …. (1)
Questa volta ci siamo riusciti!
Per essere più precisi, dovremmo sempre scrivere:
∫ xn dx = x(n+1)/(n+1) + c
Ma, d’ora in poi, potremmo anche evitare l’aggiunta di una costante qualsiasi. Basta solo NON dimenticare che essa compare sempre! Il risultato di un integrale indefinito è sempre una famiglia di funzioni e non un valore numerico come quello definito.
Abbiamo trattato il calcolo del primo integrale immediato in modo quasi “noioso”, ma è bene non cominciare a creare confusione fin dall’inizio. Gli integrali sanno farlo molto bene da soli!
Per non dimenticare di essere sempre semplici fino allo stremo, anche a costo di apparire banali, scriviamo un caso concreto:
∫ x4 dx = x5/5
E qualche caso particolare:
∫ x dx = x2/2
∫ 1· dx = ∫ x0· dx = x(0 + 1)/(0 + 1) = x
∫ k· dx = k ∫ 1· dx = k·x
La (1) vale anche per n frazionari, n negativi, ma NON per n = - 1.
Infatti avremmo:
∫ x-1 dx = x(-1 +1)/(-1+1) = 1/∞ = 0
In realtà, l’integrale di 1/x vale tutt’altra cosa (e dovreste anche saperlo…). Qual è la funzione la cui derivata è x-1 = 1/x ?
Essa altro non è che la derivata del logaritmo in base e, ossia
d(ln(x))/dx = 1/x
Per cui:
∫ x-1dx = ∫ 1/x dx = ∫ (d(ln(x))/dx) dx = ln(x)
Passiamo ora alla funzione che ha la derivata più semplice in assoluto:
f(x) = ex
La sua derivata è la stessa funzione, ossia ex
Si ha la quasi “stupida” relazione:
∫ f ’(x) dx = ∫ exdx = ex
Sapendo che la sua derivata non è altro che la stessa funzione, ne deriva che l’integrale non può che essere anch’esso la stessa funzione! Per cui:
∫ ex dx = ex
Leggermente più complicata è la funzione in cui abbiamo una costante qualsiasi elevata a x, ossia:
f(x) = ax
Basta, però, ricordare la sua derivata, che vale:
f ’(x) = ax ln(a)
Abbiamo, quindi:
∫ ax ln(a) = ax
Ma ln(a) è una costante, che può essere trasportata fuori dal segno di integrale. Segue che:
ln(a) ∫ ax = ax
E, infine:
∫ ax = ax/ ln(a)
Probabilmente, vi state meravigliando che non parli dell’integrale della funzione ln(x). Il problema è che non conosciamo nessuna funzione semplice la cui derivata sia proprio ln(x). Le proprietà degli integrali indefiniti non possono aiutarci… Ci vuole ben altro.
Non ci resta che passare alle funzioni trigonometriche. In particolare, al seno e al coseno.
f(x) = sin(x)
Per ricavarlo, ricordiamo la funzione cos(x). Qual è la sua derivata? Presto detto: - sin (x)
Abbiamo perciò:
∫ - sin(x) dx = - ∫ sin(x) dx = cos(x)
Da cui:
∫ sin(x) dx = - cos(x)
Analogamente per:
f(x) = cos(x)
La derivata di sin(x) è proprio cos(x), per cui:
∫ cos(x) dx = sin(x)
Potremmo anche concludere con la funzione
f(x) = tan(x)
Sappiamo che:
d(tan(x))/dx = 1 + tan2(x)
Possiamo allora scrivere:
∫ (1 + tan2(x)) dx = tan(x)
e ancora:
x + ∫ tan2(x) = tan (x)
∫ tan2(x) = tan (x) – x
Ma, purtroppo, non riusciamo a proseguire in modo semplice e riuscire a mettere in evidenza solo l’integrale della tangente…
No, la strada non è questa.
Come abbiamo visto, non è banale determinare facilmente l’integrale di una funzione anche semplice. Risulta ovvio che ci devono aiutare delle strategie operative diverse a secondo dei casi…
La tabella degli integrali immediati di funzioni semplici è quindi piuttosto breve…
∫ xndx = x(n +1)/(n+1) + c (per n qualsiasi, ma diverso da – 1)
∫ x-1dx = ln(x) + c
∫ ex dx = ex + c
∫ ax = ax/ ln(a) + c
∫ sin(x) dx = - cos(x) + c
∫ cos(x) dx = sin(x) + c
Non deprimiamoci più di tanto, però. Il poter ricavare immediatamente l’integrale di una potenza di x ci permette, attraverso le proprietà degli integrali indefiniti, di ricavare gli integrali di moltissimi polinomi. E questa non è cosa da poco…
Provate, ad esempio, a calcolare il seguente integrale:
∫ x4 – 3x3 + x2/2 – 2x + 3
E’ veramente banale e immediato…
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






9 commenti
Può essere questo???
Ops... avevo omesso il passaggio intermedio
e, in fondo al polinomio precedente, va aggiunto il termine "c".
attenta... rifai bene il calcolo...
Forse ho capito...
l'integrale di una costante è uguale a quella costante moltiplicata per x e poi va aggiunto il "solito" c, ovvero
la formula è sempre la stessa, per cui l'integrale di 1= xº non è altro che x(º+1)/(0 + 1) = x
bravissima!:wink:
scusa...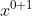 /(o+1)
/(o+1)
Tranquillo, si capiva lo stesso... questi apici sono un po' birichini!
Ti segnalo un possibile errore di scrittura:
Ma, d’ora in poi, potremmo anche evitare l’aggiunta di una costante qualsiasi. Basta solo NON dimenticare che essa compare sempre! Il risultato di un integrale indefinito è sempre una famiglia di funzioni e non un numero ben determinato.
perché la funzione 1/x è definita in tutto R tranne x=0, mentre la funzione ln(x) è definita solo per x>0. Per cui si ovvia aggiungendo il valore assoluto di x.