La lagrangiana e l'equazione di Eulero-Lagrange ***

Questo articolo è stato inserito nella pagina di approfondimento dedicata alla Meccanica Celeste.

Seguendo gli articoli di Enzo ho notato che citava l'utilizzo della "lagrangiana" per la soluzione di un problema in questo approfondimento. Avevo già visto citato questo misterioso oggetto anche da altri che ne parlavano come di una cosa fondamentale nella fisica classica e, ancora di più, nella fisica moderna. A grandi linee sapevo di cosa si trattasse, ma non avevo mai approfondito l'argomento. La citazione di Enzo mi ha incuriosito ulteriormente e ho cercato di capire meglio cosa fosse questa lagrangiana.

Per ordinare quanto sono riuscito a capire ho provato a metterlo per scritto. Gli articoli riuniti in questo approfondimento nascono da questi appunti.

Come nei trailer dei film anticipo le scene principali.

Ho giocato un po' con Harry Potter. Ovviamente non c'è nulla di magico nella lagrangiana, ma alcune volte, da come escono alcune soluzioni, sembra che un po' di magico ci sia. Non esageriamo con queste fantasie perché già Maupertuis fu preso di mira dalla satira di Voltaire per avere dato una interpretazione troppo sopranaturale al precursore della lagrangiana, non vorrei che se la prendesse anche con me.

La lagrangiana è una espressione matematica che racchiude in se tutto quello che c'è da sapere sul sistema. Una specie di DNA del problema o, visto in altro modo, lo stato del sistema che stiamo studiando. Fu trovata da Lagrange, da qui il nome, e pubblicata nel 1788 nel suo testo "Meccanica Analitica".

Per racchiudere il problema nella lagrangiana in qualche modo si usa la parola magica KappaU, infatti occorre mettere insieme energia cinetica (K) e energia potenziale (U).

La lagrangiana sarebbe interessante, ma poco utile se non avessimo uno strumento per estrarre la soluzione da questa espressione, la nostra luce Eulgrange. Lagrange ci ha dato anche questo, aiutato da Eulero. Questo strumento è fatto di una equazione, denominata equazione di Eulero-Lagrange, nella quale inserire la lagrangiana per ottenere la soluzione, cioè la posizione nel tempo delle componenti del sistema fisico che stiamo esaminando. Un caratteristica importante di questa equazione: è sempre la stessa indipendentemente dal sistema di riferimento e dalle coordinate scelte. Quindi il riferimento potrebbe essere inerziale o non; le coordinate cartesiane o di qualsiasi altro tipo. Unico vincolo è quello di usare il minimo numero di coordinate possibili per il problema, se tutti i vincoli fossero così!

Quello che mi ha sorpreso è che esista una espressione che abbia queste "magiche" proprietà. Ancora più sorprendente è che una lagrangiana esiste non solo per sistemi che sono trattabili con la meccanica classica, ma anche quando c'è di mezzo l'elettricità ed il magnetismo, quando la fisica classica non basta più ed occorre ricorrere alla meccanica quantistica o alla relatività. Anzi sembra che più si vada avanti e più la lagrangiana diventi importante. Per di più lo strumento per estrarre le soluzioni rimane sempre lo stesso. Monsù Giüsep aveva visto lontano!

Verrebbe da pensare che esiterà pure una espressione di questo genere, ma se ci sono voluti Lagrange ed Eulero per trovarla, sarà una cosa talmente complicata che è meglio lasciare perdere!

Invece non è poi così complicata, almeno in molti casi trattabili con la meccanica classica. Si tratta di ricorrere a due grandezze già viste in altri articoli: l'energia cinetica e l'energia potenziale.

Lagrangiana=energia cinetica – energia potenziale o utilizzando simboli spesso impiegati

$\large \LARGE {\color{Red} \mathfrak{L}=K-U}$

Attenzione al segno meno, non è un errore di battitura! Non è il segno più, che darebbe l'energia totale, almeno nei casi dove posso trascurare l'effetto degli altri tipi di energia. È proprio meno.

Cosa sono l'energia cinetica e l'energia potenziale è ben spiegato all'interno di questo articolo a partire da dove è collocata la figura con Maga Magò e Mago Merlino.

Per entrare meglio nello spirito del metodo di Lagrange può essere utile sentire dallo stesso Lagrange quali erano le sue intenzioni come le scrisse nella introduzione del suo libro "Meccanica Analitica" del 1788: "Ridurre la teoria della meccanica … a delle formule generali, il cui semplice sviluppo fornisce tutte le equazioni necessarie per la risoluzione del problema" e nelle avvertenze al lettore "I metodi che espongo non richiedono né costruzioni geometriche né ragionamenti geometrici o meccanici, ma soltanto operazioni algebriche". Per questa ragione nel libro non ci sono figure.

Non vorrei essere stato uno studente del prof. Lagrange!

Devo dire che c'è un limite a quanto ho affermato sopra. Non tutti i sistemi meccanici sono completamente racchiudibili in una lagrangiana. Per esserlo, non ci devono essere forze dovute all'attrito, perché queste forze non generano (o non sono generate, da un altro punto di vista) da una energia potenziale. Questo non preoccupa molto i fisici che si occupano di fisica fondamentale perché li non c'è l'attrito. Ma anche in molti altri casi i fenomeni di attrito possono essere trascurati, almeno fino ad una certa approssimazione. Questo comunque non impedisce l'applicazione del metodo di Lagrange, poiché può essere applicato anche quando ci sono queste altre forze.

Riassumo quanto ho detto finora:

la lagrangiana è una espressione che racchiude lo stato di un sistema fisico;
per i sistemi meccanici la lagrangiana è energia cinetica – energia potenziale;
esiste uno strumento per estrarre l'equazione del moto dalla lagrangiana, l'equazione di Eulero-Lagrange;
l'equazione di Eulero-Lagrange ha la stessa forma nei riferimenti inerziali e nei riferimenti non inerziali, con le coordinate cartesiane o polari o di qualsiasi altro tipo di coordinate.

Ora proseguiamo con alcuni semplici esempi per esplorare le forme che assume la lagrangiana in diversi sistemi di riferimento e con diversi tipi di coordinate. Questi esempi vorrebbero introdurre gradualmente quello che serve per applicare il metodo di Lagrange alla ricerca dei punti lagrangiani.

Per trovare la lagrangiana seguo questo procedimento:

scelgo le coordinate;
esprimo l'energia cinetica nelle coordinate scelte;
esprimo l'energia potenziale nelle coordinate scelte.

La nostra prima lagrangiana

Partiamo dal caso apparentemente più semplice. Un oggetto di piccole dimensioni tanto da poter essere approssimato ad un punto, spesso viene chiamato "punto materiale". Supponiamolo totalmente isolato, quindi non soggetto a forze e libero di muoversi in qualunque direzione.

Possiamo scegliere le usuali coordinate cartesiane per descrivere il movimento di questo punto. Non essendoci direzioni preferenziali possiamo orientare le coordinate in un modo qualunque.

L'energia cinetica è come sempre $K=\frac{1}{2} m v^2$ che dobbiamo esprimere con le sue componenti lungo le coordinate scelte (v_x,v_y,v_z). Il movimento del nostro punto è libero da vincoli, quindi la sua velocità potrebbe avere qualsiasi direzione.

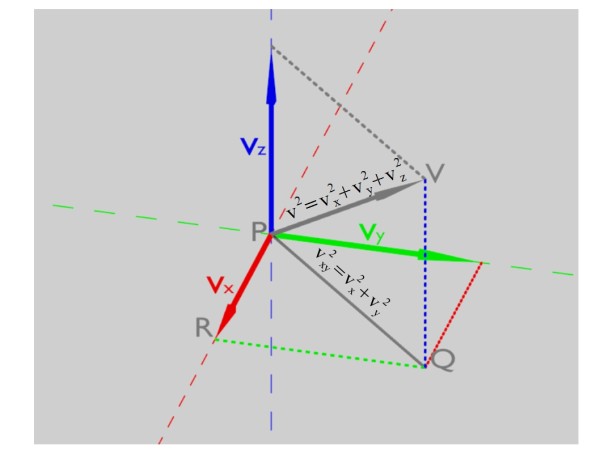
Decomponendola lungo i tre assi che abbiamo scelto si possono ottenere tutte tre le componenti diverse da zero. Le tre componenti sono perpendicolari tra loro e questo ci permette di esprimere v² applicando per due volte il teorema di Pitagora per trovare le ipotenuse prima del triangolo PRQ e poi del triangolo PQV.

Nel caso di punto materiale isolato la lagrangiana quindi sarà: ${\color{Blue} \boldsymbol{\mathfrak{L}=K=\frac{1}{2} m (v_x^2+v_y^2+v_z^2)=\frac{1}{2} m (\dot {x}^2+\dot {y}^2+\dot {z}^2)}}$

Il simbolo con il punto sopra è una notazione che risale a Newton stesso ed indica la derivata temporale (Lui avrebbe detto flussione) della funzione che sta sotto, cioè $\small \dot x=\frac{d\,x(t)}{d\,t}$ . Conviene utilizzarla perché rende più leggibili le formule che troveremo più avanti.

Questa è la nostra prima lagrangiana che di fatto non è la più semplice poiché chiama in causa tutte le componenti della velocità.

Il punto materiale libero e la gravitazione

Se il punto materiale libero di questo primo esempio lo collochiamo nei pressi della superficie terrestre occorre considerare anche l'energia potenziale gravitazionale, ma prima dobbiamo definire le nostre coordinate.

Ora c'è un orientamento preferenziale dato dalla direzione verticale della forza di gravità. Le coordinate cartesiane sembrano ancora andare bene, ma conviene allineare un asse con la verticale, diciamo l'asse z.

L'espressione dell'energia cinetica rimane invariata poiché il punto è ancora libero di muoversi in ogni direzione.L'energia potenziale gravitazionale nei pressi della superficie terrestre è:

$\large U=m\,g\,z$ ( abbiamo scelto come livello di riferimento il livello z=0).

Quindi la lagrangiana in questo caso sarà:

$\boldsymbol{{\color{Blue} \mathfrak{L}=K-U=\frac{1}{2} m (\dot {x}^2+\dot {y}^2+\dot {z}^2)-m\,g\,z}}$

Continuiamo ad esercitarci con la parola magica KappaU....

animku

.... direbbero alla scuola di magia di Hogwarts

Io proseguo con il proporvi altre lagrangiane, questa volta di corpi vincolati a seguire delle traiettorie predefinite. Vedremo come la lagrangiana semplifica questi problemi e come la scelta delle coordinate aiuta ad ottenere questa semplificazione. Forse è un argomento di poco interesse per la meccanica celeste, vincoli di questo tipo non credo se ne trovino in cielo. Le propongo perché permettono di mettere in evidenza alcune caratteristiche importanti della lagrangiana e del metodo di Lagrange. Inoltre, c'è una ragione storica poiché il metodo di Lagrange è nato proprio dallo studio di problemi con corpi vincolati.

Il procedimento è ancora lo stesso:

scelgo le coordinate;
esprimo l'energia cinetica nelle coordinate scelte;
esprimo l'energia potenziale nelle coordinate scelte.

Una corsa in slittino

carrello-rettilineo2

Parto da un esempio banale, un corpo lanciato ad una certa velocità su un binario rettilineo orizzontale senza attrito, immagino un piccolo slittino lanciato su una pista rettilinea tracciata su un lago ghiacciato vincolato in qualche modo a mantenersi aderente alla pista. Quindi lo slittino non potrà che seguire la pista.

Scelgo le coordinate con le quali descrivere la corsa dello slittino. Viene naturale scegliere come coordinata proprio l'asse della pista, i paletti rossi ci fanno da scala graduata. Diamo un nome a questa coordinata, chiamiamola w. Le altre due coordinate del nostro spazio tridimensionale non servono perché sono fissate dal vincolo di seguire la pista, basta una sola coordinata per descrivere questo caso ed una sola coordinata deve entrare nella lagrangiana.

Ora occorre esprimere l'energia cinetica del nostro slittino nelle coordinate che abbiamo scelto, in questo caso il solo asse w. Poiché lo slittino può seguire solo questo asse, la sua velocità coinciderà proprio con quella lungo questo asse.

$\large K=\frac{1}{2}mv^2=\frac{1}{2}mv_w^2=\frac{1}{2}m\dot w^2$

Ricordo che il simbolo con il punto sopra indica la derivata temporale.

Con l'energia cinetica siamo a posto. Vediamo ora l'energia potenziale.

Occorre capire quali forze sono in gioco. Allo slittino è applicata la forza di gravità (freccia gialla), ma anche la forza di reazione della pista che contrasta la forza di gravità (freccia blu). Potremmo considerare che queste forze si annullano tra loro, cosa che ci porterebbe ad ignorarle nella lagrangiana. Questo ragionamento porta ad un risultato corretto, almeno in questo caso, ma fa uso di caratteristiche specifiche del problema che stiamo vedendo. Lagrange diceva che il suo metodo avrebbe fatto uso di ragionamenti generali. Seguiamo la sua indicazione, se qui forse è eccessivo, servirà comunque per altri casi meno evidenti di questo.

Vediamo separatamente la forza di gravità e le reazioni della pista.

L'energia potenziale gravitazionale in questo caso è costante per qualsiasi posizione dello slittino.

$\large U=mgh_p$ , è infatti il prodotto di tre costanti: m, la massa dello slittino; g, l' accelerazione di gravità nei pressi della superficie terrestre; h_p, l'altezza alla quale si trova lo slittino che qui si mantiene costante al livello della pista.

Per approfondimenti sull'energia potenziale c'è questo articolo.

Nella nostra lagrangiana dovremmo sottrarre questo elemento costante, ma possiamo anche evitarlo. Il livello rispetto al quale misurare l'altezza lo possiamo scegliere noi. Ovviamente cambiando il livello di riferimento cambia il valore di U, ma non cambiano le differenze di energia potenziale tra due punti, che è ciò che conta.

Allora perché non scegliere proprio il livello della pista come livello 0? Se facciamo cosi abbiamo U=0 e ci evitiamo di portarci appresso questo elemento costante.

Niente di speciale, dovevamo trovare l'energia potenziale gravitazionale e l'abbiamo trovata. Scegliendo come livello di riferimento quello della pista abbiamo trovato che l'energia potenziale è sempre nulla e quindi non è necessario che appaia nella lagrangiana.

Ora occorre trovare l'effetto delle forze di reazione della pista e sarebbe un bel problema se non ci avessero pensato per noi Lagrange su una idea di d'Alambert. La loro soluzione è la più semplice possibile: ignoratele! Questa è una buona notizia. Qui si capisce il perché proprio lo studio di questo tipo di problemi ha dato origine alla metodo di Lagrange.

Questa utilissima possibilità vale quando il moto è vincolato ad una linea, anche se curva, o ad una superficie e le forze che questo vincolo esercita sono forze perpendicolari alla linea o alla superficie come accade quando non c'è attrito. Lagrange l'ha dimostrata e, almeno per il momento, conviene fidarci. Cercando di darmi una motivazione intuitiva ho pensato che queste forze in fondo servono a mantenere lo slittino sulla pista, ma questo già lo abbiamo messo nella nostra lagrangiana quando ci siamo limitati a considerare il movimento lungo l'asse w. È solo un tentativo di darmi una giustificazione intuitiva, niente di più.

Quindi nella lagrangiana del nostro slittino c'è solo l'energia cinetica:

$\large \boldsymbol{{\color{Blue} \mathfrak{L}=K=\frac{1}{2}m\dot w^2}}$

In questa formula ci sono racchiuse tutte le informazioni per ricavare tutti i dettagli sul movimento dello slittino. In questo caso sono la posizione dello slittino nel tempo, w(t), e la velocità dello slittino nel tempo, v_w(t) . Non abbiamo visto ancora gli strumenti per ricavare queste grandezze dalla lagrangiana, ma in questo caso il risultato è noto. La somma totale delle forze che agiscono sullo slittino è nulla, quindi continuerà a percorrere la pista mantenendo la sua velocità iniziale, fino a che l'approssimazione di ignorare l'attrito e le irregolarità della pista non reggerà più.

E se invece di una pista rettilinea avessimo una pista con delle curve?

carrello-curvilineo2 Partiamo ancora con la scelta delle coordinate da utilizzare. Sembrerebbe che qui non ce la possiamo cavare a buon mercato come nel caso precedente posizionando in modo conveniente uno degli assi delle coordinate.

Invece, sorprendentemente, possiamo trattare la lagrangiana quasi come nel caso precedente a patto che abbandoniamo le care coordinate cartesiane. In questo caso la coordinata più semplice e opportuna è ancora la pista stessa. Si è curva, ma non importa. Una delle caratteristiche della lagrangiana e del metodo che la usa è proprio quello di non essere esigente sulle coordinate da utilizzare. Gli va bene quasi tutto.

Anche su questa pista abbiamo i paletti che ci possono dare il valore della coordinata che chiamo s. Ad esempio, se i paletti sono distanziati di 100m, se passo il 5° paletto al 10° secondo, s(10)=500 ed il 7° paletto al 20° secondo s(20)=700 avrò percorso 200m in 10s. La coordinata s ci da quindi direttamente la distanza percorsa. La velocità media, che è la distanza diviso il tempo impiegato a percorrerla sarà:

$\large \bar {v}=\frac{s(t_2)-s(t_1)}{t_2-t_1}$ , che nell'esempio è 20 m/s.

Per intervalli di tempo piccoli, tendenti a 0, diventa la derivata di s rispetto a t, cioè la velocità istantanea che possiamo utilizzare per calcolare l'energia cinetica:

$\large \begin{aligned} v & = \frac {ds}{dt}=\dot s \\ K & =\frac{1}{2}mv^2=\frac{1}{2}m \dot {s}^2 \end{aligned}$

Ora dovremmo trovare l'energia potenziale. Siamo in una situazione molto simile a quella dell'esempio precedente. L'energia potenziale gravitazionale è costante e quindi possiamo evitare di inserirla nella lagrangiana. Anche in questo caso il moto è vincolato ad una linea e le forze sono perpendicolari a questa linea. Quindi anche qui possiamo trascurare queste forze.

La differenza è che qui, oltre alle forze viste prima, ci sono anche le forze orizzontali che la pista esercita sul nostro slittino quando lo fa curvare per seguire il tracciato della pista. Queste forze sono comunque perpendicolari alla direzione della pista, stiamo sempre vedendo un caso ideale nel quale possiamo ignorare l'attrito e considerare lo slittino abbastanza piccolo da assimilarlo ad un punto. A differenza del caso precedente, queste forze orizzontali non sono compensate, infatti fanno deviare lo slittino dal percorso rettilineo, e gli fanno seguire la traiettoria curvilinea della pista. Comunque Lagrange ci permette di ignorarle nella lagrangiana.

La lagrangiana anche in questo caso è data dalla sola energia cinetica:

$\large {\color{Blue} \boldsymbol{\mathfrak{L} =K =\frac{1}{2}m \dot {s}^2 }}$

Non abbiamo ancora la luce Eulgrange, pardon gli strumenti per ricavare dalla lagrangiana il moto dello slittino. Ma già possiamo ottenere qualche informazione solo confrontando la lagrangiana di quest'ultimo esempio con quella della pista rettilinea dell'esempio precedente.

$\large \mathfrak{L}=\frac{1}{2}m \dot{w}^2 \;\;\;\;\mathfrak{L}=\frac{1}{2}m \dot{s}^2$

Sono uguali, c'è solo s al posto di w. Se è vero che nella lagrangiana c'è tutto e gli strumenti per ricavarlo sono sempre gli stessi, allora s(t) e ṡ(t) devono avere lo stesso andamento di w(t) e ẇ(t) del caso precedente. Quindi lo slittino manterrà la sua velocità iniziale anche in questo caso, ma dovendo percorrere una traiettoria curvilinea cambierà continuamente direzione per mantenere la velocità tangente alla pista.

Ora che ci siamo scaldati con questi casi semplici, vediamo un caso dove su una traiettoria vincolata agisce l'energia potenziale.

La lagrangiana di un corpo vincolato quando agisce la gravità: il pendolo

pendolo1 Si tratta di un pendolo che idealizziamo assumendo che l'asta sia di massa trascurabile, che non ci siano attriti e che il pendolo possa oscillare solo su un piano verticale.

La traiettoria è quindi una curva circolare disposta verticalmente. Ricordando l'esempio precedente potrei scegliere una coordinata che segue la circonferenza, l'origine potrebbe essere nella posizione allineata con la verticale. Credo che andrebbe bene, ma in questo caso ci può essere utile utilizzare l'angolo θ per quando dovremo trovare l'energia potenziale. Non è che sia essenziale visto che l'angolo è la lunghezza dell'arco diviso il raggio, $\bg_white \large \theta = \frac {s}{r}$ , ma così vediamo anche una coordinata che non rappresenta una lunghezza.

L'energia cinetica, come visto sopra, è:

$\bg_white \large K =\frac{1}{2}mv^2=\frac{1}{2}m \dot {s}^2$

Dovremo rendere esplicito l'angolo θ in questa relazione. Sostituiamo ad s la sua espressione con θ e deriviamola rispetto al tempo, tenendo conto che qui r è costante:

$\bg_white \large \begin{aligned} s & = r\, \theta \\ \dot{s} & = \frac {d\, r \theta}{dt} = r \frac {d\, \theta}{dt}= r \dot \theta \end{aligned}$

Ora mettiamola nell'espressione dell'energia cinetica.

$\bg_white \large K =\frac{1}{2}\, m\, {\color{Blue} \dot {s}^2}=\frac{1}{2}\, m\, {\color{Blue} r^2 {\dot {\theta}}^2}$

Con l'energia cinetica ci siamo, ora passiamo all'energia potenziale.

Nel caso che stiamo vedendo possiamo considerare costante l'accelerazione dovuta alla gravità poiché il movimento del pendolo modifica di pochissimo la sua distanza dal centro della Terra. In questi casi l'energia potenziale dipende direttamente dall'altezza alla quale si trova la massa. L'altezza può essere misurata a partire da un livello arbitrario. Ovviamente cambiando il livello di riferimento cambia il valore di U, ma non cambiano le differenze di energia potenziale tra due punti, che è ciò che conta. Prendendo come riferimento l'altezza minima del pendolo avremo

U=mgh.

La lagrangiana sembrerebbe dipendere da due variabili θ ed h. Ma queste variabili non sono indipendenti: se varia una, forzatamente varia anche l'altra in modo determinato. Si tratta di trovare questa relazione. Dalla figura si può vedere come h dipende da θ:

$\large \bg_white h=r (1-\cos (\theta ))$

Quindi la lagrangiana di questo sistema è:

$\bg_white \large \boldsymbol{ {\color{Blue} \mathfrak{L}=K-U=\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2 - m g r (1- cos(\theta))}}$

In questi ultimi tre esempi abbiamo visto alcune lagrangiane di corpi vincolati a seguire traiettorie predefinite. Questi vincoli applicano delle forze di reazione all'oggetto che stiamo studiando che complicano il problema perché sono delle incognite aggiuntive. In assenza di attrito, queste forze possono essere considerate perpendicolari al vincolo e la lagrangiana consente di ignorarle. In questi casi è sufficiente un'unica coordinata anche curvilinea per descrivere il moto. L'energia cinetica e l'energia potenziale vanno espresse rispetto a questa coordinata.

Verso Eulgrange: le derivate della equazione di Eulero-Lagrange

Ora che abbiamo ottenuto una bella lagrangiana come quella del pendolo, come fare ad estrarre le informazioni che contiene?

Non è molto difficile, anzi spesso è più semplice di altri metodi. Ricordate la luce Eulgrange all'inizio di questo articolo?

La lagrangiana deve essere inserita in una equazione individuata da Lagrange utilizzando un risultato che aveva ottenuto in precedenza Eulero, l'equazione di Eulero-Lagrange.

L'equazione di Eulero-Lagrange ci dice come elaborare la lagrangiana per ottenere l'equazione del moto. Questa elaborazione richiede di fare alcune derivate della lagrangiana.

Cosa siano e come si facciano le derivate si trova molte bene spiegato nella serie di articoli elencati dal 23 al 30 in questo approfondimento. Per questo articolo non serve ricordare tutta la teoria delle derivate. Bastano poche cose: una tabella delle derivate notevoli dove ci sono i "prototipi" delle derivate più comuni (magari teniamola a portata di mouse aprendola su una nuova scheda), ricordare come si fa la derivata di una operazione (somma, differenza, prodotto e quoziente) tra due funzioni e come si fa la derivata di una funzione composta e poco altro.

A prima vista le derivate della equazione di Eulero-Lagrange hanno un aspetto che potrebbe intimorire, ma dietro l'apparenza non c'è niente di particolarmente difficile rispetto a quelle ben spiegate da Enzo nel suoi articoli.

Occorre solo farci l'abitudine.

Per iniziare a familiarizzare con queste derivate, ho pensato di proporvi questo percorso suddiviso in tre tappe che ci avvicina alla equazione di Eulero-Lagrange. Strada facendo incontreremo uno degli aspetti che mi ha inizialmente confuso e vedrete che l'apparenza inganna.

Allora, se vi va, partiamo verso la prima tappa!

percorso

1a-tappa

Appuntatevi le vostre risposte alla domanda di questa tappa prima di passare alla tappa successiva. Questa è solo la prima tappa, al contrario dei telequiz, sarà l'ultima risposta quella che conta.

Quali sono le derivate delle funzioni elencate sotto?

per ciascuna elenco 3 possibilità

$\begin{aligned}&\frac{w^2}{2}\;\; \; \; \; &A: 0, \,\;\; \; \; \; \; \; \; &B:w, &C: w\dot w \; \; \; \; \; \; \\ &\cos(\theta )\;\; \; \; \; &A: -\sin(\theta ), \; \,&B:0, &C: -\dot \theta \sin(\theta )\\ &2\sqrt{s\;} &A: \frac{\dot s}{\sqrt{s}} ,\; \; \,&B:0, &C: \frac{1}{\sqrt{s}} \; \; \; \; \end{aligned}$

In caso di dubbi c'è sempre la possibilità di consultare gli articoli di Enzo. Tra le derivate notevoli c'è la derivata di xⁿ, considerate che n non è necessario sia intero, ad esempio può essere anche 1/2.

Se hai finito la seconda tappa è qui.

percorso

2a-tappa

In questa seconda tappa iniziamo a ragionare sulle possibili derivate di una lagrangiana.

Prendiamo la lagrangiana del pendolo, che riscrivo in questo modo:

$\bg_white \large { { \mathfrak{L}=\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2 - m\, g\, r + m\, g\, r \cos(\theta)}}$ , dove m g ed r sono costanti.

Ricordo che il simbolo con il punto sopra indica la derivata rispetto al tempo.

Questa è la domanda.

Rispetto a quali variabili si può derivare questa lagrangiana ottenendo un risultato non nullo?

Una è evidente nella formula. Una non si vede nella formula, o meglio, si intravede in un punto, ma è inesorabilmente presente. Un'altra può non sembrare una variabile, ma piace molto a Lagrange.

Forse a prima vista non sembra, ma questa domanda ha molto a che fare con la domanda della prima tappa.

Se hai finito la terza tappa è qui.

percorso

3a-tappa

lookingbackward

In questa terza tappa diamo una occhiata indietro al percorso fatto.

Nella seconda tappa abbiamo esplorato la possibilità di derivare una funzione come la lagrangiana rispetto a diverse variabili.

Dopo l'esperienza della seconda tappa riconsideriamo la domanda della prima tappa.

Quali sono le derivate delle funzioni elencate sotto?

Per ciascuna elenco 3 possibilità
$\begin{aligned}&\frac{w^2}{2}\;\; \; \; \; &A: 0, \,\;\; \; \; \; \; \; \; &B:w, &C: w\dot w \; \; \; \; \; \; \\ &\cos(\theta )\;\; \; \; \; &A: -\sin(\theta ), \; \,&B:0, &C: -\dot \theta \sin(\theta )\\ &2\sqrt{s\;} &A: \frac{\dot s}{\sqrt{s}} ,\; \; \,&B:0, &C: \frac{1}{\sqrt{s}} \; \; \; \; \end{aligned}$

È una domanda completa? Manca qualcosa nella domanda?

Se avete dato una risposta nella prima tappa, quale è o quali sono le domande complete alle quali avete realmente risposto?

Si fa presto a dire derivata, ma quale?

L'obiettivo di questo piccolo percorso era quello di abituarsi a vedere derivate di una stessa funzione fatte rispetto a diverse variabili. Probabilmente lo avevate già capito. Accade spesso per le grandezze fisiche come la lagrangiana che dipendono da più variabili come posizione, tempo, velocità. Nella equazione di Eulero-Lagrange c'è tutto il campionario e oltre...

Le soluzioni proposte nella domanda della prima tappa possono essere tutte derivate della funzione della prima colonna e solo questione rispetto a quale variabile è fatta la derivata. Ad esempio, prendo la funzione $\dpi{120} \bg_white F=\frac{w^2}{2}$ , la posso derivare rispetto a w, la posso derivare rispetto al tempo t o la posso derivare rispetto ad un'altra variabile, chiamiamola z, che non ha alcuna influenza su w:

$\dpi{120} \bg_white \begin{align*} \frac{dF}{dw}&= \frac{d}{dw}\frac{w^2}{2} =w \\ \frac{dF}{dz} &= \frac{d}{dz}\frac{w^2}{2} = 0 \\\frac{dF}{dt}&= \frac{d}{dt}\frac{w^2}{2} = \frac{d}{dw} \frac{w^2}{2}\;\frac{dw}{dt}=w \dot w\end{align*}$

A chi ha meno confidenza con le derivate può venire la voglia di capire meglio come si ottengono le tre derivate.

Teniamo a portata di mouse la tabella delle derivate notevoli dove ci sono i "prototipi" delle derivate più comuni e la derivata di una funzione composta, che comunque ripeto più avanti. Eseguo i passaggi in modo esteso commentandoli.

$\dpi{120} \bg_white \frac{d}{dw}\frac{w^2}{2} =\underbrace{\frac{1}{2}\frac{dw^2}{dw}}_{1}=\frac{1}{2}\underbrace{2w^{2-1}}_{2}=w$

una costante può essere portata fuori della derivata
ho applicato il prototipo della derivata rimasta: $\dpi{100} \bg_white \frac{dx^n}{dx}=nx^{n-1}$

$\dpi{100} \bg_white \frac{d}{dz}\frac{w^2}{2} = 0$

F non dipende da z. La derivata è 0 poiché qualsiasi variazione di z non fa variare F. Qui vediamo anche che non sempre se la derivata di una funzione è nulla la funzione è una costante, potrebbe essere una funzione di variabili diverse da quella di derivazione.

$\dpi{120} \frac{d}{dt}\frac{w^2}{2} = \underbrace{\frac{d}{dt}\frac{w(t)^2}{2}}_1=\underbrace{\frac{d}{dw} \frac{w^2}{2}\;\frac{d\,w(t)}{dt}}_2=\underbrace{w \dot w}_3$

la variabile w la vedo come una funzione del tempo. Pensate alla coordinata dello slittino vista in uno degli esempi di lagrangiana. E' certamente un funzione del tempo, anzi è proprio la funzione che stiamo cercando. Quindi questa è una funzione di funzione $\dpi{100} \bg_white F(g(x))$ dove $\dpi{100} \bg_white F=\frac{w^2}{2}$ e $\dpi{100} \bg_white g(x)=w(t)$
applico il prototipo di derivata di funzione di funzione $\dpi{100} \bg_white \frac{d\,F(g(x))}{dx}=\frac{d\,F(g)}{dg}\frac{d\,g(x)}{dx}$
la derivata del primo termine è quella trovata sopra, la derivata del secondo la scrivo in modo più compatto

Conviene continuare a ragionare ancora sulla funzione $\dpi{100} \bg_white F(w(t))=\frac{w(t)^2}{2}$ per capire meglio il significato fisico della sua derivata e poi fare un altro passo avanti.

Pensiamo w come la coordinata che indica la posizione di un oggetto in movimento ed F come una grandezza fisica che dipende dalla posizione. Tanto per rendere la situazione più tangibile, immaginiamo che w sia il chilometraggio lungo una strada ed F la temperatura misurata lungo questa strada.

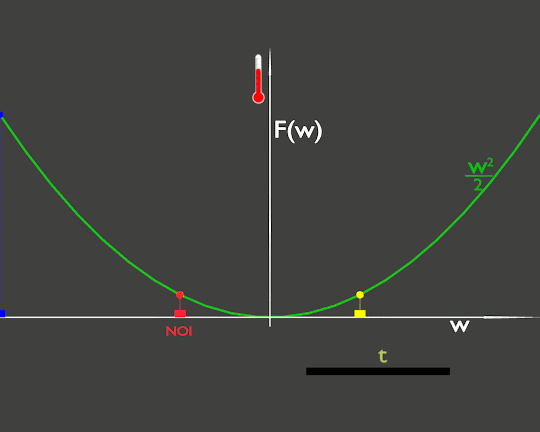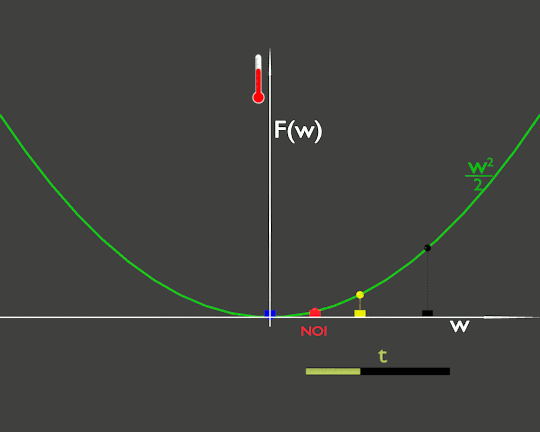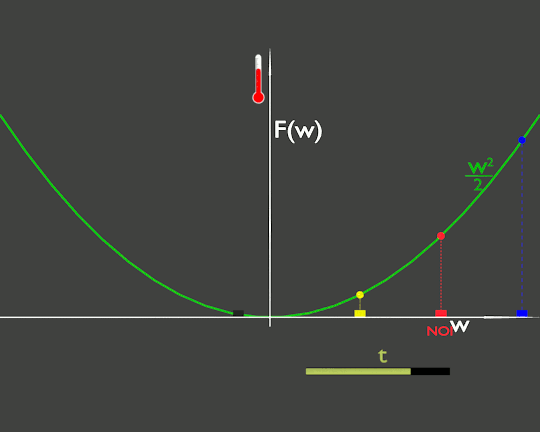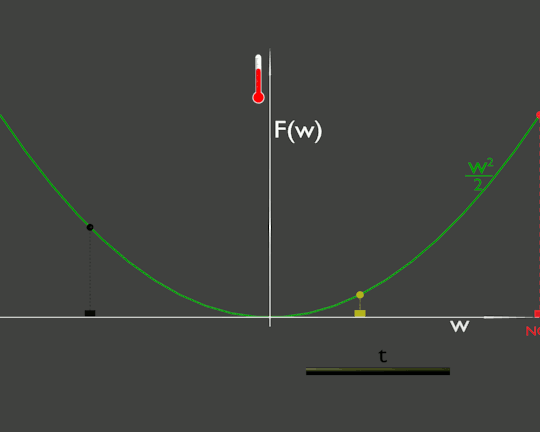
Ora percorriamo questa strada con la nostra auto che identifichiamo con il rettangolino rosso della figura. La nostra posizione, w(t), è una funzione del tempo. Osservando il termometro della nostra auto vedremmo che la temperatura varia nel tempo. Graficamente è rappresentata dall'altezza del cerchietto rosso che segue l'andamento della funzione F(w).

In realtà la temperatura dell'ambiente non sta cambiando, il grafico (verde) della temperatura rimane sempre lo stesso, ma siamo noi che ci stiamo spostando da zone più fredde a zone più calde o viceversa.

La rapidità di variazione della temperatura dipende dalla nostra velocità, infatti nella derivata sopra appare a moltiplicatore $\bg_white \dot w$ . La variazione di temperatura vista dall'auto blu che ci sta sorpassando è più rapida della nostra e quella dell'auto nera che percorre la strada nel verso opposto è opposta alla nostra.

Vedendo il termometro che sale potremmo domandarci: è la temperatura dell'ambiente che sta salendo o sono io che mi sto spostando in una zona più calda?

La risposta si può ottenere facilmente. Mi fermo alla prima piazzola di sosta, come l'auto gialla, e continuo ad osservare il termometro. Nel caso che stiamo vedendo la temperatura rimane costante, infatti il cerchietto giallo nella animazione è fermo. Dal punto di vista matematico è dovuto al fatto che F(w) non dipende esplicitamente dal tempo, ma dipende dal tempo solo tramite w. Se la nostra w(t) è costante, cioè siamo fermi, rimane costante anche F(w).

Per avere un paragone vediamo cosa accade se fosse la temperatura dell'ambiente che cambia, per semplificare la facciamo cambiare uniformemente nello spazio. Questo è rappresentato da una funzione F(t) che dipende esplicitamente dal tempo t e non dipende esplicitamente da w. Nella figura $\dpi{100} \bg_white F(t)=\frac{t^2}{2}$

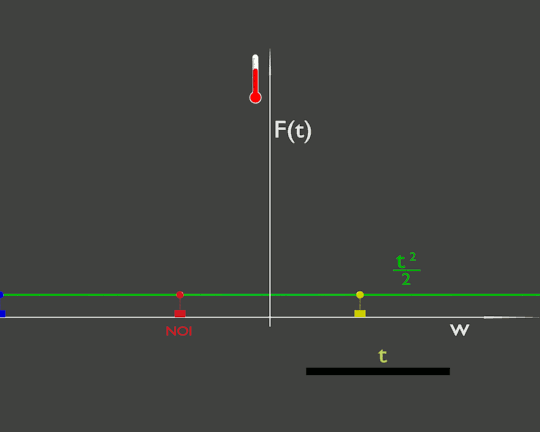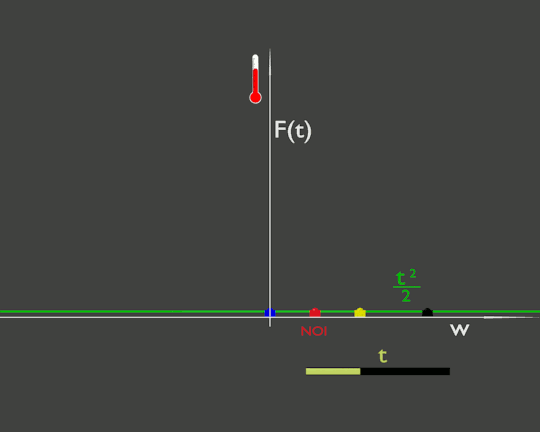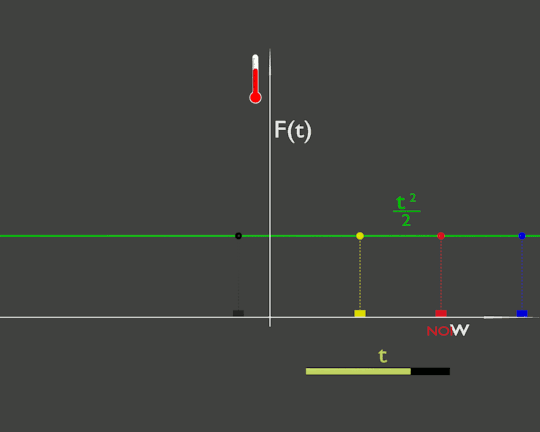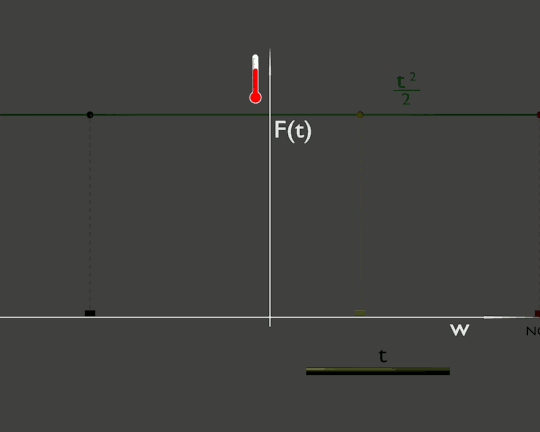
Anche qui la temperatura che misura la nostra auto (cerchietto rosso) varia, ma perché sta variando la temperatura dell'ambiente, la linea verde che si muove, e non perché ci stiamo muovendo.

In questo caso anche se ci fermiamo, come l'auto gialla, la temperatura continuerà a cambiare.

Questa operazione di fermarsi e trovare come varia una grandezza lasciando scorrere solo il tempo in matematica si chiama derivata parziale rispetto al tempo e viene indicata con questo simbolo: $\dpi{150} {\color{Blue} \boldsymbol{\frac{\partial F}{\partial t}}}$ .

Quindi non meravigliatevi se vi capiterà di vedere un cartello come questo.

Qui ci siamo concentrati sul tempo, ma la derivata parziale si può fare rispetto ad ogni altra variabile.

Il procedimento matematico per farla è semplice. Devo fare la derivata della funzione considerando solo la variabile scelta dove appare esplicitamente e non dove appare implicitamente in un altra variabile (come t in w(t)), considerando quindi tutte le altre variabili costanti. Nel nostro caso abbiamo fissato la posizione fermando la nostra auto, ma in generale tutte le altre variabili dalle quali può dipendere la funzione sono considerate costanti non solo quelle della posizione.

Quindi, nel nostro primo caso:

$\dpi{120} \begin{align*}\frac{\partial}{\partial t}\frac{w^2}{2} &=0 \;\;\textrm{ mentre }\;\; \frac{d}{dt}\frac{w^2}{2} ={w \dot w}\\ \end{align*}$

La derivata parziale è nulla perché t non appare esplicitamente e tutto il resto deve essere considerato costante. Nel secondo caso t appare esplicitamente quindi la derivata parziale non è nulla:

$\dpi{120} \frac{\partial}{\partial t}\frac{t^2}{2} =t \ \ \textrm{ e }\ \ \frac{d}{dt}\frac{t^2}{2} ={t}$

Le due derivate sono uguali poiché in questa funzione non ci sono altre variabili oltre alla variabile di derivazione t.

Per distinguerla dalla derivata parziale, l'altro tipo di derivata è chiamata derivata totale.

Con questo abbiamo fatto la conoscenza con tutti i tipi di derivata contenuti nella equazione di Eulero-Lagrange.

Aggiungo una postilla per vedere un caso più generale rispetto ai due visti sopra. Non è necessario per la prossima puntata, ma non è male vederlo.

Nei due casi visti c'era una funzione, F, e due variabili, w e t. La funzione F dipendeva esplicitamente da una sola delle due variabili, F(w) ed F(t). Tra le parentisi sono elencate le variabili dalle quali la funzione dipende esplicitamente.

C'è anche la possibilità che possa dipendere esplicitamente da tutte due le variabili, F(w,t), come ad esempio

$\dpi{120} \bg_white F(w,t)=\frac{w^2}{2}+t$ e $\dpi{120} \bg_white F(w,t)=\frac{w^2}{2}t$

Ora che conosciamo le derivate parziali è possibile scrivere in una forma più generale la derivata di una funzione di funzione in modo che sia valida anche per queste funzioni di funzioni.

$\dpi{120} \bg_white \frac{d}{dt}F(w,t)=\frac{\partial}{\partial w}F(w,t)\,\frac{dw}{dt}+\frac{\partial}{\partial t}F(w,t)$

Se ci fossero altre variabili, per ciascuna si dovrebbe aggiungere un termine del tipo di quello per w.

Per chi volesse continuare a ragionare su queste derivate propongo alcune domande.

Quali sono le derivate parziali $\dpi{120} \bg_white \frac{\partial}{\partial t}F(w,t)$ e totali $\dpi{120} \bg_white \frac{d}{d t}F(w,t)$ delle due funzioni $\dpi{120} \bg_white F(w,t)=\frac{w^2}{2}+t$ e $\dpi{120} \bg_white F(w,t)=\frac{w^2}{2}t$ ?

Se nella espressione della derivata totale al posto di F(w,t) ci fosse una F(t), l'espressione può essere scritta eliminando un termine. Come?

Stessa domanda con F(w) al posto di F(w,t).

Ora che li abbiamo domati, i draghi delle derivate non appaiono più così terribili. Anzi possiamo cavalcarli per farci portare dalla equazione di Eulero-Lagrange.

Fabricius usa la pietra Lagrangiana per risolvere i problemi. Con la parola magica KappaU li chiude nella pietra che colpita dalla luce Eulgrange emette la soluzione.

Noi ci dobbiamo accontentare del metodo di Lagrange che attraverso l'energia cinetica (K) e l'energia potenziale (U) ci fa costruire la lagrangiana. La lagrangiana elaborata con l'equazione di Eulero-Lagrange ci fornisce la soluzione.

Finora abbiamo costruito alcuni esempi di lagrangiane di corpi liberi e vincolati (qui e qui) ed abbiamo preso confidenza con le derivate che sono utilizzate nella equazione di Eulero-Lagrange (qui).

A questo punto, finalmente, arriviamo alla equazione di Eulero-Lagrange. Ed ora...

..... squillino le trombe, rullino i tamburi,

ecco a voi l'equazione di Eulero-Lagrange!

$\dpi{200} \bg_white {\color{Red} \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot q}-\frac{\partial \mathfrak{L}}{\partial q}=0}$

C'è tutto il campionario delle derivate, ma ormai abbiamo imparato a conoscerle. Per esorcizzare ogni timore residuo vediamole una ad una ed applichiamole alla lagrangiana del pendolo.

$\bg_white \large { { \mathfrak{L}=\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2 - m\, g\, r + m\, g\, r \cos({\color{Blue} \theta})}}$

Il termine $\dpi{120} \bg_white \frac{\partial \mathfrak{L}}{\partial q}$ è la derivata rispetto alle variabili che abbiamo scelto come coordinate per descrivere il problema. Come spesso accade, ho chiamato genericamente q questa variabile. q può essere la w o la s della pista della slitta, la θ del pendolo o qualsiasi altra variabile che avessimo scelto di utilizzare. Questa è una caratteristica importante. L'equazione è sempre la stessa indipendentemente da tipo di coordinate, dalle cartesiane alle polari a qualsiasi altro tipo di coordinata che segua l'andamento del vincolo.

Ora applichiamo questa derivata alla lagrangiana del pendolo.

In questo caso la nostra q è θ, quindi dobbiamo fare la derivata della lagrangiana rispetto a θ. Dobbiamo preoccuparci solo dei termini dove compare esplicitamente proprio θ , gli altri termini hanno derivata nulla. Questo è sostanzialmente quello che abbiamo visto ci dice di fare il simbolo ∂.

$\bg_white \large \begin{aligned} \frac {\partial \mathfrak{L}}{\partial \theta} & = \underbrace {\frac {\partial}{\partial \theta}(\frac{1}{2}\, m\, r^2 {\dot {\theta}}^2)}_0 - \underbrace {\frac {\partial}{\partial \theta} ( m g r )}_0 +\underbrace {\frac {\partial}{\partial \theta}(m g r\, {\color{Blue} \cos(\theta)})}_{m g r{\color{Blue} (-\sin(\theta))}}\\\frac {\partial \mathfrak{L}}{\partial \theta}&= - m g r \sin(\theta) \end{aligned}$

Nel primo termine c'è $\boldsymbol{\dot \theta}$ che deve essere considerata come una variabile diversa da θ. Inizialmente questo mi ha confuso, ma ci si fa l'abitudine. Quindi la derivata del primo termine rispetto a θ è nulla. Tanto più la derivata del secondo termine dove θ non c'è proprio. Rimane il terzo termine. La derivata del coseno è il seno con il segno negativo (nel dubbio abbiamo sempre la scheda con le derivate più utili).

Il termine $\dpi{120} \bg_white \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot q}$ è la derivata rispetto al tempo di una derivata parziale rispetto a $\dpi{120} \bg_white \dot q$ .

Partiamo dalla derivata parziale. Sembra una cosa strana poiché è una derivata fatta rispetto ad una variabile che è esse stessa una derivata, ricordiamo che $\dpi{120} \bg_white \dot q$ è la derivata rispetto al tempo di q. Se però la consideriamo semplicemente come un'altra variabile, allora valgono le solite regole. Applichiamola ancora alla lagrangiana del pendolo:

$\dpi{120} \bg_white \begin{aligned} \frac {\partial \mathfrak{L}}{\partial \dot \theta} & = \underbrace {\frac {\partial}{\partial \dot \theta}(\frac{1}{2}\, m\, r^2 {\color{Blue} {\dot {\theta}}^2})}_{\frac{1}{2} m r^2 {\color{Blue} 2 \dot \theta}} - \underbrace {\frac {\partial}{\partial \dot \theta} ( m g r )}_0 +\underbrace {\frac {\partial}{\partial \dot \theta}(m g r cos(\theta))}_{0}\\\frac {\partial \mathfrak{L}}{\partial \dot \theta}&= m r^2 \dot \theta \end{aligned}$

Le derivate del secondo e terzo termine sono nulle perché non contengono $\dpi{120} \bg_white \dot \theta$ . La derivata del primo termine si ottiene dal solito prototipo già visto, $\dpi{100} \bg_white \frac{dx^n}{dx}=nx^{n-1}$

Ora occorre fare la derivata rispetto al tempo. Il simbolo d ci chiede di individuare non solo dove la variabile di derivazione t è esplicitamente presente, ma anche tutto ciò che può variare con il tempo. Applichiamolo ancora al pendolo:

$\dpi{120} \bg_white \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}=\frac{d}{dt}m r^2 \dot \theta=m r^2 \frac{d \dot \theta}{dt}=m r^2 \ddot \theta$

Qui il tempo non compare esplicitamente, ma $\dpi{120} \bg_white \dot \theta$ può variare nel tempo, cioè può essere una funzione non costante del tempo, $\dpi{120} \bg_white \dot \theta(t)$ . Invece m ed r nella lagrangiana del pendolo sono costanti. L'ultimo passaggio segue ancora la notazione di Newton che aggiunge un punto sopra la variabile per ogni derivata rispetto al tempo.

Ora rivediamo l'equazione di Eulero-Lagrange completa.

$\dpi{120} \bg_white \begin{aligned} \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}&-\frac{\partial \mathfrak{L}}{\partial \theta} =0 \\ m r^2 \ddot \theta &+mgrsin(\theta)=0\\ \ddot \theta =&- \frac {g}{r} sin(\theta) \ \textup{ equivalente a } \frac{d^2\theta}{dt^2}=- \frac {g}{r} sin(\theta) \end{aligned}$

Questa è l'equazione differenziale che descrive il moto. Per trovare come θ varia nel tempo, cioè la funzione θ(t), occorre risolvere questa equazione differenziale.

Ovviamente non è differente dalla equazione ottenuta con altri metodi, ad esempio analizzando la geometria del sistema ed applicando direttamente le equazioni di Newton. Non potrebbe essere differente altrimenti uno dei metodi sarebbe sbagliato. In effetti, alcune volte ciò che si ottiene appare differente, ma è solo una diversa forma della stessa espressione.

pendolo1

Qui ci siamo arrivati utilizzando il metodo di Lagrange e la lagrangiana attraverso alcuni passi che possiamo seguire in ogni altro problema. Ripercorriamoli per avere una visione d'insieme del metodo:

scelgo le coordinate: serve una sola coordinata per descrivere il moto ed abbiamo scelto l'angolo θ che segue la traiettoria di P
esprimo l'energia cinetica (K) nelle coordinate scelte: $\mathrm{la\, velocit\grave{a}\; di\; P\; \grave{e}}\; r\dot \theta \;\textrm{ quindi la sua l'energia cinetica sar} \mathrm{\grave{a}} \; K=\frac{1}{2} m (r\dot \theta )^2$
esprimo l'energia potenziale (U) nelle coordinate scelte: $U=mgh=mg\,r(1-\cos (\theta))$
inserisco K ed U nella espressione della lagrangiana:
$\dpi{120} \bg_white {\color{Blue} \mathfrak{L}=K-U}=\frac{1}{2} m (r\dot \theta )^2-\left (mg\,r-mg\,r\cos (\theta) \right )$
inserisco la lagrangiana nella equazione di Eulero-Lagrange:
$\dpi{120} \bg_white {\color{Blue} {\frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot \theta}-\frac{\partial \mathfrak{L}}{\partial \theta}=0}}$
$\dpi{120} \bg_white {{\frac{d}{dt}\frac{\partial}{\partial \dot \theta}\left ( \frac{1}{2} m (r\dot \theta )^2-mg\,r+mg\,r\cos (\theta) \right )-\frac{\partial}{\partial \theta}\left ( \frac{1}{2} m (r\dot \theta )^2-mg\,r+mg\,r\cos (\theta) \right )=0}}$
sviluppo le derivate ed ottengo l'equazione differenziale che governa il moto:

$\dpi{120} \bg_white \begin{aligned} &\frac{d}{dt}\left (m r^2 \dot \theta \right )-\frac{\partial \mathfrak{L}}{\partial \theta} =0 \\ &m r^2 \ddot \theta +mgrsin(\theta)=0\\ &\ddot \theta =- \frac {g}{r} sin(\theta) \end{aligned}$

Mi sembra che il metodo rispetti le intenzioni di Lagrange "Ridurre la teoria della meccanica … a delle formule generali, il cui semplice sviluppo fornisce tutte le equazioni necessarie per la risoluzione del problema" , "I metodi che espongo non richiedono né costruzioni geometriche né ragionamenti geometrici o meccanici, ma soltanto operazioni algebriche". Forse sul semplice potremmo non essere totalmente convinti, ma per il resto...

Per trovare esplicitamente come θ varia nel tempo, cioè la funzione θ(t), occorre risolvere l'equazione differenziale: $\dpi{120} \ddot \theta =- \frac {g}{r} sin(\theta)$ .

I matematici ci dicono che la soluzione esiste, ma non possiamo scriverla come una normale funzione. Quindi mi fermo qui citando Eulero (forse abusivamente in questo caso, ma suona bene) "Se non ci è permesso di penetrare fino ad una conoscenza completa del movimento non è alla meccanica e all'insufficienza dei principi conosciuti che bisogna attribuire la causa, ma è la stessa analisi che qui ci abbandona". Se lo diceva Eulero...

Ora abbiamo tutti gli elementi per tornare al punto di partenza. La frase di Enzo nell'articolo sui punti lagrangiani che mi aveva inizialmente incuriosito: "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana". Prima dovremo passare per un esempio di applicazione del metodo di Lagrange ad un sistema non inerziale che finora non abbiamo visto. Incontreremo una nostra vecchia conoscenza che ci inizierà a svelare qualcosa della frase di Enzo.

Lagrange sulla giostra: un riferimento non inerziale

Finora abbiamo visto il metodo di Lagrange in sistemi di riferimento inerziali, cioè fermi o in moto rettilineo uniforme. Ma il metodo di Lagrange si può applicare pari-pari anche quando si scelgono riferimenti non inerziali. Vediamo un caso semplice.

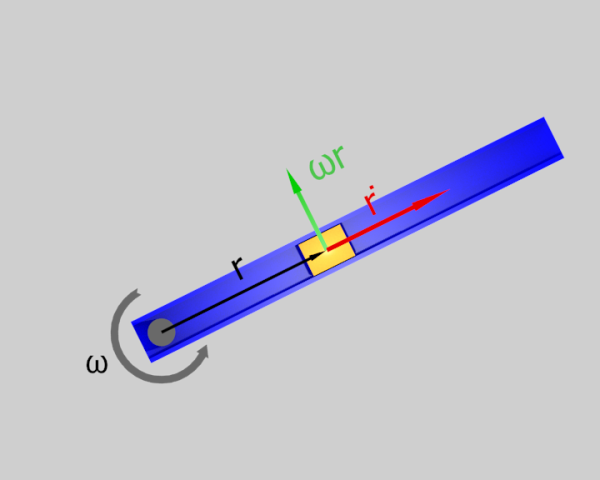binariorotante Abbiamo un binario orizzontale che ruota attorno ad un asse verticale con velocità angolare uniforme. Una giostra molto essenziale. Mettiamo sul binario un oggetto che scivola senza attrito, una saponetta. Vediamo cosa ci dice il metodo di Lagrange in questa situazione.

Applichiamo anche in questo caso il solito procedimento.

Scelgo le coordinate

Il vincolo costringe il movimento lungo la linea del binario, quindi basta una sola coordinata per definire il movimento. Come nei casi della slitta verrebbe naturale scegliere come coordinata proprio il binario con l'origine messa nel punto di incontro con l'asse di rotazione. Però c'è una differenza importante con i casi precedenti: qui il binario è in movimento, per di più ruota. Questo riferimento è un riferimento non inerziale. Bene, il metodo di Lagrange è applicabile senza modifiche anche in questo caso, richiede solo un po' più di attenzione nel trovare l'energia cinetica e potenziale. Dobbiamo sempre ragionare nel sistema di riferimento inerziale e poi esprimere le grandezze trovate con le coordinate scelte.

Esprimo l'energia cinetica K con la coordinata scelta

Il binario costringe l'oggetto a rimanere al suo interno, quindi il movimento sarà lungo la coordinata che abbiamo scelto. Se chiamiamo questa coordinata r, possiamo indicare la velocità in questo sistema di riferimento con $\dot r=\frac{dr}{dt}$ .L'oggetto fa anche un altro movimento poiché segue il binario nella sua rotazione. La velocità di questo movimento è $\boldsymbol{r \dot \theta}$ come abbiamo visto per il pendolo. Qui però la variabile è r, mentre la velocità angolare ha un valore costante che chiamo ω, $\boldsymbol{\dot \theta=\omega}$ . Bisogna comporre queste due velocità per ottenere la velocità totale. Fortunatamente le due velocità sono perpendicolari tra loro. Per ottenere il quadrato dell'ampiezza della velocità, che è quello che ci serve per l'energia cinetica, possiamo applicare il teorema di Pitagora.

$K=\frac{1}{2}mv^2=\frac{1}{2}m\left ( {\color{Blue} \dot{r}^2}+\omega ^2{\color{Red} r^2} \right )$

L'energia cinetica è composta di due termini. Li coloro per seguirne meglio l'evoluzione.

Il primo termine ha una forma già vista, $\frac{1}{2}m \dot{r}^2$ . Come nei casi precedenti contiene il quadrato della derivata della variabile rispetto al tempo, $\large \dot r$ . Questo termine è l'energia cinetica come appare nel riferimento non inerziale ruotante con il binario, possiamo chiamarlo energia cinetica apparente.

Il secondo termine, $\frac{1}{2}m\omega ^2{\color{Red} r^2}$ , non contiene come al solito la derivata della variabile, ma la variabile stessa al quadrato. Teniamolo d'occhio perché è un tipo sospetto.

Esprimo l'energia potenziale (U) nelle coordinate scelte

In questo caso non ci sono forze attive da considerare e quindi l'energia potenziale può essere considerata nulla.

In realtà ci sono la forza che fa ruotare il binario e la forza che il binario esercita sulla nostra saponetta. Ma, come al solito, le forze riguardanti il vincolo possono essere ignorate.

Altre forze non ce ne sono nel sistema di riferimento inerziale.

Inserisco K ed U nella espressione della lagrangiana

Qui c'è solo K.

$\boldsymbol{\mathfrak{L}}=K-U=\frac{1}{2}m\left ( {\color{Blue} \dot{r}^2}+\omega ^2{\color{Red} r^2} \right )$

Inserisco la lagrangiana nella equazione di Eulero-Lagrange

$\begin{aligned}& \frac{d}{dt}\frac{\partial \mathfrak{L}}{\partial \dot r}-\frac{\partial \mathfrak{L}}{\partial r}=0 \\ &\frac{d}{dt}{\frac{\partial }{\partial \dot r}[\frac{1}{2} m ({\color{Blue} {\dot r}^2}+r^2\omega^2)]}-{\frac{\partial }{\partial r}[\frac{1}{2} m ({\dot r}^2+{\color{Red} r^2}\omega^2)]}=0 \end{aligned}$

Sviluppo le derivate ed ottengo l'equazione differenziale che governa il moto

$\begin{aligned} &\frac{d}{dt}\underbrace{\frac{\partial }{\partial \dot r}[\frac{1}{2} m ({\color{Blue} {\dot r}^2}+r^2\omega^2)]}_{\frac{1}{2} m ({\color{Blue} 2\dot r}+0)}-\underbrace{\frac{\partial }{\partial r}[\frac{1}{2} m ({\dot r}^2+{\color{Red} r^2}\omega^2)]}_{\frac{1}{2}(0+{\color{Red} 2r} \omega^2)}=0 \\ & m {\color{Blue} \frac{d\dot r}{dt}}- m{\color{Red} r}\omega^2=0 \\ &m {\color{Blue} \ddot r}=m {\color{Red} r} \omega^2 \end{aligned}$

E qui avremmo risolto il problema. Questa è l'equazione differenziale da risolvere per trovare come si muove la nostra saponetta, cioè r(t). Peraltro è uno dei rari casi nei quali la soluzione può essere espressa in forma analitica.

Fermiamoci ancora un attimo sulla equazione ottenuta per esaminare i termini che la compongono.

Il termine a sinistra, $m {\color{Blue} \ddot r}$ , è la massa dell'oggetto moltiplicata per l'accelerazione lungo la coordinata r. Un osservatore nel sistema di riferimento ruotante, che vede la nostra saponetta accelerare, può considerare il termine a destra, $m {\color{Red} r} \omega^2$ , come la forza che causa l'accelerazione. In effetti è una vecchia conoscenza, è la forza centrifuga che appare nei riferimenti non inerziali ruotanti.

Ma noi non avevamo messo forze nella lagrangiana.

Allora da dove è comparsa questa forza?

Seguendo la traccia rossa nelle equazioni viste sopra troviamo che viene da $\frac{\partial }{\partial r}\left ( \frac{1}{2}m\, \omega^2 {\color{Red} r^2} \right )$ . Avevamo inserito l'argomento della derivata come una componente della energia cinetica nel riferimento inerziale. Questo stesso termine si comporta come una energia potenziale se visto dal riferimento non inerziale ruotante. L'energia potenziale prodotta dalla forza centrifuga. Nel riferimento ruotante potremmo pensare la lagrangiana come composta da una energia cinetica vista in questo riferimento, $\frac{1}{2}m\, \dot{r}^2$ , ed una energia potenziale (fittizia), $-\frac{1}{2}m\, \omega^2 {\color{Red} r^2}$ .

${\mathfrak{L}}=\frac{1}{2}m\, \dot{r}^2-\left (-\frac{1}{2}m\, \omega^2 {\color{Red} r^2} \right )=K_a-U_a$

E' proprio una caratteristica della lagrangiana quella di aiutare a scoprire collegamenti inattesi tra grandezze fisiche come quello visto qui tra energia cinetica ed energia potenziale in diversi riferimenti.

Finalmente sono arrivato al problema che ha originato questo articolo.

La lagrangiana alle prese con i lagrangiani

Il sistema fisico è quella descritto in questo articolo dove c'è l'animazione che ci ricorda che il sistema è ruotante.

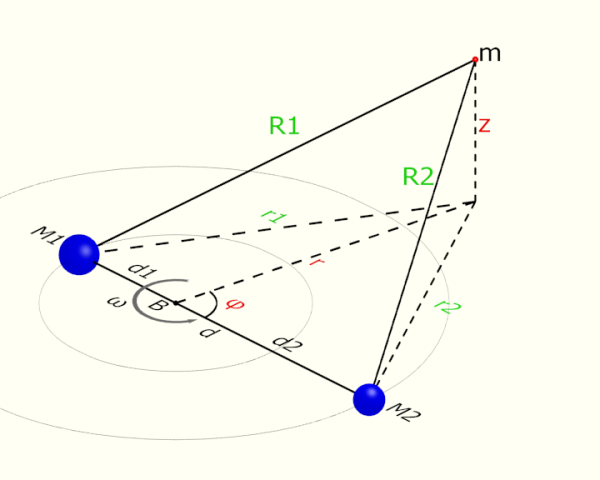
Abbiamo tre corpi che esercitano reciprocamente l'attrazione gravitazionale. Il problema consiste nel trovare una configurazione nella quale i tre corpi possano ruotare intorno al comune centro di massa mantenendo costanti le reciproche distanze, come se fossero un corpo rigido.

In un sistema di riferimento che ruota con i tre corpi sarebbero quindi fermi.

Il problema è semplificato da due approssimazioni:

la massa del terzo corpo (m) è trascurabile rispetto a quella degli altri due
i due corpi di massa maggiore (M1 e M2) sono in orbite circolari intorno al centro di massa.

Queste approssimazioni permettono di trattare il moto di M1 ed M2 come se m non ci fosse. Quindi il loro moto lo possiamo considerare un dato del problema invece di essere parte del problema. Per la terza legge di Keplero la velocità angolare ω è legata alla massa dei due corpi maggiori ed alla loro distanza dalla relazione $\small \omega^2=G\frac{(M1+M2)}{d^3}$

Allora possiamo applicare la solita procedura concentrandoci solo su m.

Scelgo le coordinate

In questo problema m non è vincolato a seguire alcuna traiettoria. Si può muovere liberamente sul piano di rotazione di M1 e M2, ma anche uscire dal piano. Servono quindi 3 coordinate per descrivere il suo movimento. In questo caso scelgo di utilizzare le coordinate cilindriche. Le posizioniamo con l'asse z perpendicolare al piano di rotazione per sfruttare meglio le simmetrie della configurazione. Quindi la posizione di m è definita dalle 3 coordinate (r,φ,z) come si vede nella figura. Nella stessa figura ho evidenziato il verde le distanze che dipendono da queste coordinate, R1, R2, r1, r2.

Esprimo l'energia cinetica K con le coordinate scelte

$K=\frac{1}{2} m \left( {\color{Red} \dot r}^2+ {\color{Red} r}^2 \left( \omega+{\color{Red} \dot \varphi}\right)^2 + {\color{Red} \dot z}^2 \right)$

I movimenti lungo le coordinate (r,φ,z) sono in ogni istante perpendicolari tra loro. Quindi possiamo applicare il teorema di Pitagora per ottenere il quadrato della velocità totale. L'unica avvertenza è che la velocità di rotazione ${\color{Red} \dot \varphi}$ si aggiunge a quella del riferimento, ω.

Esprimo l'energia potenziale (U) con le coordinate scelte

L'energia potenziale di m è dovuta alla contemporanea attrazione di M1 ed M2. I potenziali gravitazionali sono sommabili. Cioè l'energia potenziale di m è la somma di quelle prodotte da M1 ed M2. Questo ci permette di scrivere:

$U=U1({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})+U2({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})=-G m \frac{M1}{{\color{DarkGreen} R1}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})}- G m \frac{ M2}{{\color{DarkGreen} R2}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})}$

Al momento non conviene sostituire R1 ed R2 con le loro espressioni complete per non appesantire inutilmente la formula. Ricordiamo solo che sono funzioni delle coordinate.

Inserisco K ed U nella espressione della lagrangiana

$\mathfrak{L}=K-U=\left ( \frac{1}{2} m \left( {\color{Red} \dot r}^2+ {\color{Red} r}^2 \left( \omega+{\color{Red} \dot \varphi}\right)^2 + {\color{Red} \dot z}^2 \right) \right )-\left (-G m \frac{M1}{{\color{DarkGreen} R1}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})}- G m \frac{ M2}{{\color{DarkGreen} R2}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})} \right )$

Proviamo anche qui a prendere il punto di vista del sistema di riferimento ruotante separando l'energia cinetica apparente dal resto.

$\mathfrak{L}=\left [ \frac{1}{2} m \left( {\color{Red} \dot r}^2 + + {\color{Red} r}^2 {\color{Red} \dot \varphi}^2+{\color{Red} \dot z}^2\right) \right ] +m\,{\color{Red} r}^2 \omega\, {\color{Red} \dot \varphi}-{\color{DarkBlue} \left [-\frac{1}{2}m\,{{\color{Red} r}}^{2}\omega^2-G m \frac{M1}{{\color{DarkGreen} R1}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})}- G m \frac{ M2}{{\color{DarkGreen} R2}({\color{Red} r},{\color{Red} \varphi},{\color{Red} z})} \right ]}$

Nel temine più a destra, Ua, ho accorpato gli addendi che conosciamo fare parte dell'energia potenziale vista dal riferimento non inerziale, inclusa l'energia potenziale centrifuga vista nell'esempio precedente.

Credo che si riferisse a questo sviluppo la frase di Enzo "Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana" scritta nell'articolo sui punti lagrangiani .

In effetti l'abbiamo ottenuta dall'energia cinetica e l'energia potenziale gravitazionale nel riferimento inerziale e da queste è emerso il comportamento nel riferimento non inerziale solo riorganizzando la lagrangiana.

Vediamo anche gli altri termini. Quello più a sinistra è l'energia cinetica come appare nel riferimento ruotante.

C'è anche il termine al centro che non è bene collocabile. Sicuramente non fa parte dell'energia cinetica apparente, ma non sta bene neanche nell'energia potenziale, almeno per come la conosciamo, perché non dipende solo dalla posizione ma dipende anche dalla velocità. Ce lo dovevamo aspettare sapendo che ci sono altre forze apparenti oltre alla forza centrifuga. Forze apparenti che dipendono dalla velocità come la forza di Coriolis. In effetti quel termine è proprio il potenziale che genera la forza di Coriolis. Esce anche questa dalla lagrangiana. È un potenziale un po' diverso da quello gravitazionale o centrifugo. Lasciamolo separato da Ua.

Inserisco la lagrangiana nelle equazioni di Eulero-Lagrange

Trovata l'energia potenziale si potrebbe passare direttamente a trovare i punti di equilibrio ricordando che si trovano nei punti stazionari dell'energia potenziale.

$\frac{\partial U_a({ r},{ \varphi},{\color{Red} z})}{\partial {\color{Red} z}}=0$ $\frac{\partial {U_a}\left( r,{\color{Red} \varphi},z\right)}{\partial{\color{Red} \varphi}}\, =0$ $\frac{\partial U_a({ {\color{Red} r}},{ \varphi},{ z})}{\partial {\color{Red} r}}=0$

Ma, per seguire fino in fondo il metodo di Lagrange, provo a farmi dire cosa fare dalle equazioni di Eulero-Lagrange. Chi volesse saltare lo sviluppo successivo che conferma le tre equazioni e traccia la loro risoluzione può continuare qui.

Questa volta le equazioni sono 3, una per ciascuna coordinata.

Partiamo con la coordinata z: $\frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial \mathfrak{L}}{\partial {\color{Red} \dot z}}-\frac{\partial \mathfrak{L}}{\partial {\color{Red} z}}=0$

Ci interessano gli addendi che contengono ${\color{Red} z}$ o ${\color{Red} \dot z}$ , gli altri hanno derivata nulla.

$\frac{1}{2}m\frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial {\color{Red} \dot z}^2}{\partial {\color{Red} \dot z}}-\frac{\partial[-U_a({ r},{ \varphi},{\color{Red} z})]}{\partial {\color{Red} z}}=0$

$m{\color{Red} \ddot z}=-\frac{\partial U_a({ r},{ \varphi},{\color{Red} z})}{\partial {\color{Red} z}}$ questa è una delle 3 equazioni del moto.

In modo analogo si può arrivare alle altre due equazioni del moto.

$\frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial \mathfrak{L}}{\partial {\color{Red} \dot \varphi}}-\frac{\partial \mathfrak{L}}{\partial {\color{Red} \varphi}}=0$ $m\, {{r}^{2}}\, {\color{Red} \ddot \varphi}+2\, m\, r\, \dot r \, {\color{Red} \dot \varphi} =-\frac{\partial}{\partial{\color{Red} \varphi}}\, {U_a}\left( r,{\color{Red} \varphi},z\right)-2\, m\, r\, \dot r \,\omega$

$\frac{\mathrm{d} }{\mathrm{d} t}\frac{\partial \mathfrak{L}}{\partial {\color{Red} \dot r}}-\frac{\partial \mathfrak{L}}{\partial {\color{Red} r}}=0$ $m{\color{Red} \ddot r}-m\, {\color{Red} r}\dot \varphi^2=-\frac{\partial U_a({ {\color{Red} r}},{ \varphi},{ z})}{\partial {\color{Red} r}}+2 m\, {\color{Red} r}\omega\dot \varphi$

Le tre equazioni sono complesse per la presenza dell'effetto di Coriolis, ultimo termine a destra, e per le espressioni delle accelerazioni nel sistema di riferimento utilizzato (termini a sinistra).

Ricordiamo però il nostro problema. Stiamo cercando i punti di equilibrio, cioè quei punti dove se mettiamo m questo ci dovrebbe rimanere. Per avvenire questo occorre che in quei punti le accelerazioni siano nulle quando la velocità sono nulle.

Quindi annulliamo velocità ed accelerazioni nelle tre equazioni sopra ed otteniamo:

$-\frac{\partial U_a({ r},{ \varphi},{\color{Red} z})}{\partial {\color{Red} z}}=0$ $-\frac{\partial {U_a}\left( r,{\color{Red} \varphi},z\right)}{\partial{\color{Red} \varphi}}\, =0$ $-\frac{\partial U_a({ {\color{Red} r}},{ \varphi},{ z})}{\partial {\color{Red} r}}=0$

Abbiamo ancora la conferma che il metodo di Lagrange permette di trovare le equazioni del moto solo con sviluppi matematici.

Risolvendo questo sistema di tre equazioni si ottengono i punti lagrangiani. Lo ha già fatto Enzo in dettaglio nel suo articolo.

Per chi volesse arrivarci dalle tre equazioni viste sopra, la traccia che ho seguito è questa.

Dalla prima equazione si ottiene che le soluzioni sono sul piano z=0, cioè sul piano di rotazione di M1 ed M2.

Dei 3 addendi di Ua, il primo non dipende da z. Rimangono quindi solo il 2° ed il 3° .

$\small \frac{\partial }{\partial {\color{Red} z}}\left (\frac{1}{2}m\,{{\color{Red} r}}^{2}\omega^2+\frac{M1}{{\color{DarkGreen} R1}({ r},{\varphi},{\color{Red} z})}+ \frac{ M2}{{\color{DarkGreen} R2}({ r},{ \varphi},{\color{Red} z})} \right )=0$ , con $\small {{\color{DarkGreen} R1}({ r},{ \varphi},{\color{Red} z})} =\sqrt{r1({ r},{ \varphi})^2+{\color{Red} z}^2}$ e $\small {{\color{DarkGreen} R2}({ r},{ \varphi},{\color{Red} z})} =\sqrt{r2({ r},{ \varphi})^2+{\color{Red} z}^2}$

Facendo le derivate si ottiene $\small \frac{M1\, {\color{Red} z}}{[{r1({ r},{ \varphi})^2+{\color{Red} z}^2}]^{3/2}}+ \frac{ M2\,{\color{Red} z}}{[{r2({ r},{ \varphi})^2+{\color{Red} z}^2}]^{3/2}} =0$ che ha come unica soluzione reale $\small {\color{Red} z}=0$

Sul piano z=0, Ua si presenta con un andamento simile a quello in questa figura. I punti lagrangiani sono sulle cime delle colline e nelle selle. Per trovarne la posizione occorre ricorrere alle altre due equazioni.

Dalla seconda equazione si ricava che le soluzioni sono su due rete. Una è la retta che passa per M1 ed M2 (φ=0 e φ=π). L'altra è la retta equidistante da M1 ed M2 $\left (r \cos(\varphi)=\frac{d}{2}-d1=\frac{d2-d1}{2} \right )$ . Che equivale a dire che le distanze r1 ed r2 della figura precedente devono essere uguali.

La terza equazione permette di identificare i punti di equilibrio su queste due rette.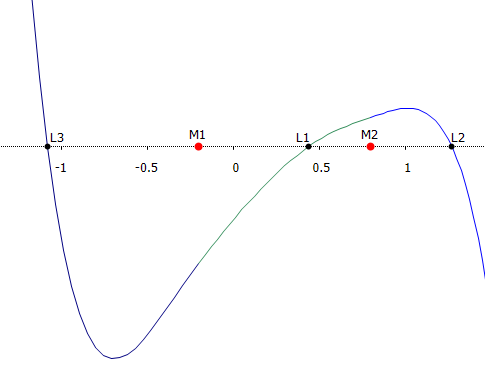

Inserendo la condizione della prima retta (φ=0 e φ=π) si ottiene una equazione risolvibile solo numericamente. Il grafico è del tipo di quello affianco. Le intersezioni del grafico con l'asse x sono le coordinate dei punti lagrangiani L1, L2 e L3.

Un avviso per chi volesse effettuare i passaggi per arrivare a questa equazione. In realtà ho dovuto considerare 3 equazioni a causa delle combinazioni di segni necessarie per convertire il modulo delle distanze di m da M1 ed M2 in una forma gestibile algebricamente.

Inserendo la condizione della seconda retta $\left (r \cos(\varphi)=\frac{d}{2}-d1 \right )$ si ottiene che $r=\sqrt{{{{d1}}^{2}}-d\,{d1}+{{d}^{2}}}$ . Detto in modo più interessante, M1, M2 ed m devono essere ai vertici di un triangolo equilatero.

Ci sono due punti con questa caratteristica denominati L4 ed L5.

Al termine di questo sviluppo, mi fermo ancora un attimo sulla seconda e terza equazione per darne una interpretazione fisica. 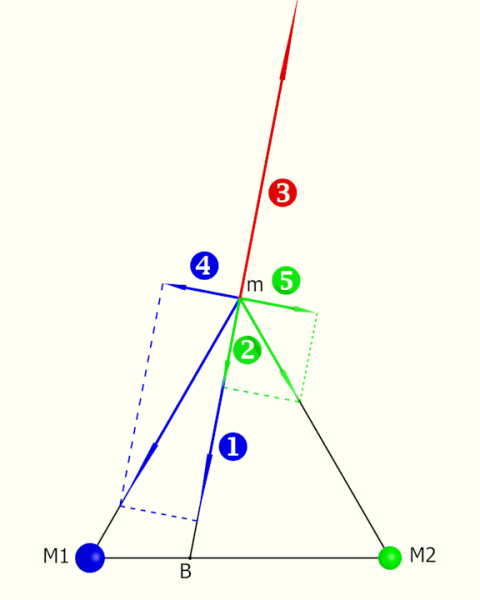Le scrivo nella forma che già ingloba la condizione di essere sul piano z=0 trovata nello sviluppo visto sopra.

Ricordiamo che la derivata dell'energia potenziale lungo una direzione è l'opposto della forza lungo quella direzione.

La prima dice che la somma delle componenti radiali dell'attrazione dei due corpi maggiori su m, (1) e (2), deve uguagliare la forza centrifuga, (3). La seconda ci dice che le componenti tangenziali della forze di attrazione, (4) e (5), devono annullarsi. Questo è spesso il punto di partenza del ragionamento per la ricerca dei punti lagrangiani. Con il metodo di Lagrange queste condizioni emergono come risultato dal solito sviluppo della lagrangiana senza alcun ragionamento fisico o geometrico aggiuntivo.

Ho evidenziato questa caratteristica del metodo di Lagrange perché era proprio lo scopo che Lagrange si era prefisso. Ricordate? L'ho già citato più volte. Quello che abbiamo visto può essere un ulteriore esempio. Abbiamo applicato il metodo. Nelle soluzioni abbiamo trovato inglobata la forza centrifuga e la disposizione delle forze di gravità che agiscono su m nei punti di equilibrio. Non è stato necessario che mettessimo noi queste grandezze fisiche e configurazioni geometriche nel nostro ragionamento.

A questo punto ringrazio chi mi ha accompagnato fin qui. Questi esempi hanno cercato di dare un'idea di cosa sia la lagrangiana e di come possa essere utilizza. In realtà abbiamo visto solo un lato della medaglia. Ce n'è anche un altro nel quale la lagrangiana svela un aspetto della natura che può sembrare preveggenza, quello che Maupertuis interpretò come un intervento sopranaturale. Chissà, potrebbe essere il sequel di questa serie di articoli.

Qui potrete trovare una applicazione del metodo di Lagrange ad un altro caso interessante con un riepilogo ed una integrazione degli argomenti trattati in questo articolo.

11 commenti

pippo

04/01/2018 at 16:21

Bell'articolo
Fabrizio

11/01/2018 at 10:12

Grazie Pippo per l'apprezzamento.

Fabrizio
MASSIMO SOTTOCORNOLA

09/10/2018 at 17:43

Argomento difficile per curiosi appassionati che come me hanno poca dimestichezza con la matematica ma reso comprensibile da una ottima esposizione
Fabrizio

10/10/2018 at 23:23

Massimo, ti ringrazio per il tuo messaggio che coglie proprio la ragione che mi ha portato a scrivere l'articolo. Da curioso appassionato (prendo a prestito questa tua definizione che trovo molto bella) volevo condividere con altri curiosi appassionati quello che avevo capito seguendo lo spunto dato da Enzo sulla lagrangiana. Certamente la nostra curiosità su questi argomenti si può scontrare con la matematica che li descrive. Ma quello è il linguaggio della natura, come ci ha insegnato Galilei.
Nell'articolo ho cercato di aiutare ad affrontare questa difficoltà più che tentare di evitarla. D'altra parte nel caso della lagrangiana evitare l'aspetto matematico credo porterebbe ad illustrazioni che lascerebbero ampiamente insoddisfatta la nostra curiosità. Ma questo credo accada anche per molti altri temi dell'astronomia e della fisica in generale.
Il mio contributo a questo circolo è molto limitato. Ma ci sono altri contributori che in molti loro articoli, consultabili nell'archivio, vanno nella direzione di accompagnarci ad affrontare i temi più complessi, spesso matematici, di ciò che ci appassiona. Il primo fra tutti ovviamente è Enzo, il fondatore del circolo, ma fortunatamente non è il solo. Un esempio possono essere i numerosi articoli di Umberto sulla matematica pura. Certamente è l'aspetto di questo circolo che trovo più interessante e spero che il già ricco insieme di argomenti trattati si possa gradualmente estendere anche ad argomenti via via più impegnativi.
Fabrizio

24/09/2019 at 23:22

Qui potrete trovare una applicazione del metodo di Lagrange ad un altro caso interessante con un riepilogo ed una integrazione degli argomenti trattati in questo articolo.
Alberto Salvagno

03/01/2021 at 19:48

Purtroppo diverse formule non risultano più leggibili, ma sono riuscito ugualmente a seguire il filo logico fino alla fine e la lagrangiana non mi appare più come un mostro. Spero che possiate risistemare l'articolo in breve tempo per seguire bene i passaggi. Comunque grazie e complimenti
Fabrizio

05/01/2021 at 10:47

Alberto,

grazie per l'apprezzamento e per la segnalazione del problema.
mario maurizio

18/05/2021 at 23:11

ben fatto...profondo ....esaustivo....merita di riprenderlo e rimeditarlo ...grazie
Fabrizio

20/05/2021 at 09:43

Mario, grazie per il commento.
Fabio

03/06/2021 at 23:54

Articolo bellissimo perchè esposto in maniera molto comprensibile. A questo punto lancio una sfida a tutti, riuscire a spiegare con la stessa semplicità di Fabrizio, la trottola di Lagrange in maniera esaustiva (cicloide del vertice della trottola).
Fabrizio

04/06/2021 at 12:02

Fabio, grazie per l'apprezzamento dell'articolo. L'idea di darsi come obiettivo la spiegazione della trottola di Lagrange è bella, ma molto sfidante. Permetterebbe di vedere la lagrangiana applicata a corpi rigidi, ma gli sviluppi necessari mi sembrano impegnativi. Renderli comprensibi ai non addetti ai lavori non è facile. Al momento io non riesco a dedicarmici. Benvenga, se qualcun altro volesse accogliere la sfida. Ovviamente tra questi altri ci sei anche tu.

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

La lagrangiana e l'equazione di Eulero-Lagrange ***

Articoli correlati

Perché il problema dei tre corpi è caotico ? **

(Q) Consegna al volo (con soluzione)**

Soluzione della pallina lanciata in alto **

un problemino di Feynman *

11 commenti

Lascia un commento Cancel Reply