Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Inseriamo, per ultimo, l’articolo relativo ai punti lagrangiani che, forse, da un punto di vista puramente fisico, doveva essere il primo. Poco male, dato che accorperemo i quattro articoli in uno solo negli Approfondimenti. Ciò che diremo è in parte già stato affrontato in varie occasioni e in particolare nell’articolo dove si era definito il campo gravitazionale di una singola massa, la famosa ragnatela. Aggiungiamo anche, per i meno preparati, qualche discorso sull’energia meccanica. Poi finalmente ci dedichiamo alla doppia ragnatela … energetica.

Ciò che faremo tra poco è quello di considerare la ragnatela (trattata QUI) attraverso grandezze diverse, decisamente più fisiche,  che permetteranno un’applicazione diretta ai sistemi binari stretti, uno degli argomenti più caldi  e fondamentali dell’evoluzione stellare.

Andiamo avanti con ordine, cercando di definire al meglio i parametri coinvolti. Per far ciò avremmo, in realtà, bisogno di descrivere buona parte della Meccanica, ma cercheremo di limitarci ai concetti fondamentali che qua e là abbiamo già usato e descritto. Per chi volesse una visione generale e completa, non posso che far riferimento al libro “La Fisica addormentata nel Bosco”. Tuttavia, dato che la mia “bontà” è ormai qualità ben nota a tutti (ah ah ah…), inseriamo una trattazione molto elementare e abbastanza completa dedicata all’energia, una delle grandezze più importanti e più ambigue dell’Universo (del cui principio di conservazione QUI abbiamo dato una spiegazione-favola adatta a grandi e piccoli)

La ragnatela gravitazionale

Un piccolo richiamo... Nell'articolo sulla ragnatela singola, siamo stati capaci di eliminare la massa della particella  e trattare le caratteristiche  solo sulla base della massa centrale .

Non abbiamo fatto altro che confermare ciò che Galileo sapeva benissimo: la cinematica dei corpi che vengono intrappolati nella ragnatela non dipende assolutamente dalla massa della preda. In parole ben più note: una sfera di cotone e una di piombo cadono al suolo con la stessa velocità.

Torniamo, allora, al nostro campo gravitazionale e vediamo di raddoppiarlo, ossia mettiamo quasi a contatto due ragni con le loro ragnatele. Purtroppo, esse si “mescolano”, creando una configurazione piuttosto intricata. Per studiarla al meglio utilizziamo la nostra massa unitaria e vediamo cosa le può succedere.

A ogni punto da lei occupato viene associato un vettore (una lezione sui vettori la trovate QUI), di intensità uguale all’accelerazione di gravità, comandata dalla forza di gravità, diretto verso il centro della stella. Il suo valore lo conosciamo molto bene:

a_G = GM/r²

Se la ragnatela fosse unica, avremmo una situazione molto semplice come quella di Fig. 1.

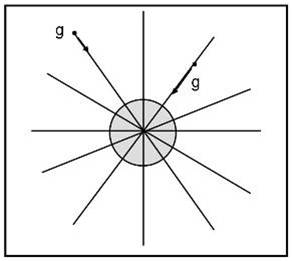
Il problema è che adesso i ragni sono due e due sono le loro trappole, sovrapposte tra loro. Calma e sangue freddo. Cerchiamo di ricordare cosa sono le linee di forza di un campo gravitazionale. Esse sono le linee che congiungono la massa unitaria e la massa centrale (il ragno). In altre parole, sono le linee che la massa seguirebbe se fosse lasciata in balia della ragnatela. Nel caso della singola ragnatela, queste linee sono ovvie e vengono descritte dalle rette disegnate in Fig. 1. Le linee di forza e loro tangenti sono la stessa cosa, ma possiamo anche concludere che i vettori accelerazione gravitazionale sono in ogni punto tangenti alle linee di forza.

Se i ragni sono due, non ci resta che valutare le accelerazioni di gravità delle due masse-ragni in modo indipendente e poi sommare i due vettori. Quello finale è l’accelerazione dovuta a entrambe le ragnatele e la linea di forza corrispondente non sarà altro che la curva tangente alla retta in quel punto. Lavorando in questo modo, la ragnatela finale, dovuta all’intersezione delle due ragnatele, si costruisce con grande semplicità come rappresentato in Fig. 2.

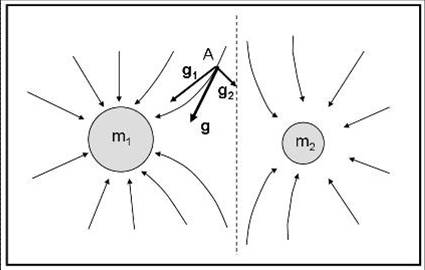
Le linee di forza non sono più semplici come prima. La motivazione è ovvia: i due campi gravitazionali si sovrappongono. I punti più critici sono quelli vicini al limite tra le due ragnatele (linea tratteggiata). Nel caso della figura, la massa m₁ è maggiore di m₂ e quindi un punto posto a pari distanza dalle due masse-ragni, tende a cadere verso la più massiccia (l’accelerazione di gravità cresce con la massa che l’esercita).

Se il punto è in una certa posizione tra le due stelle la situazione diventa “imbarazzante”. Imbarazzante, nel senso che il punto ha un grande imbarazzo su dove cadere… rimane più o meno in sospeso in una sorta di equilibrio. Ma andiamo con calma e non crediamo di essere già arrivati ai punti lagrangiani. Ci siamo, infatti, dimenticati che le due masse ruotano attorno al proprio baricentro e le condizioni di equilibrio diventano una cosa ben più complicata Soprattutto, pensiamo che l’applicazione all’evoluzione stellare ha bisogno di qualcosa di più fisico.

Dobbiamo fermarci qui e prendere una decisione. Passare subito alle superfici equipotenziali o introdurre con molta calma una grandezza fisica di importanza veramente unica: l’energia. Solo lei, infatti, permette di delineare una situazione che abbia applicazioni veramente “pratiche” nei casi di due masse molto vicine. E’ vero, la conosciamo bene e l’abbiamo usata molto spesso, ma -forse- senza che tutti i lettori possano veramente darle del “tu”.

Per alcuni, quindi, la parte che viene inserita adesso è solo un piccolo ripasso, ma per altri può essere utile per chiarire concetti non sempre completamente digeriti. Avete già capito che ho deciso di partire proprio dall’inizio e i più preparati non se ne abbiano a male e saltino pure i prossimi capitoli (ma so che non lo faranno…).

Una definizione quasi impossibile

Cari amici, se c’è una cosa difficile da definire in fisica è proprio la sua attrice più importante: l’energia.

Ricordate il vecchio cartone animato di Walt Disney “La Spada nella Roccia”? Vi è la celebre battaglia tra Maga Magò e Mago Merlino. Le armi che usano sono quelle della trasformazione. La prima cerca di diventare sempre più grande e spaventosa, il secondo sempre più piccolo e apparentemente inoffensivo. Ancora una volta vincerà il microcosmo… ma a noi interessa il fatto che la capacità di agire e di vincere si basa sull’abilità di trasformarsi senza mai perdere la propria efficacia globale.

Ebbene, l’energia è qualcosa del genere. Permette di agire, ma si trasforma continuamente e la sua stessa definizione diventa sfuggente e ambigua. Quanto lo sia in realtà ce lo ha mostrato la dinamica relativistica (QUI), ma le cose non sono da meno anche nella fisica classica. In questo caso, possiamo eliminare qualche problema, trattando solo con l’energia meccanica, quella che ci serve in prima approssimazione. L’energia, allora, ha solo due possibilità di trasformazione: energia cinetica ed energia potenziale. Per la nostra trattazione semplificata bastano e avanzano.

Tentiamo allora una definizione estremamente tecnica che è più che sufficiente allo scopo. Iniziamo con l’energia cinetica, la più immediata e banale.

L’energia di chi si muove

Tutte le volte che una forza agisce, provocando lo spostamento di un corpo, compie un lavoro. quest’ultimo necessita di una certa capacità intrinseca. Questa capacità rappresenta l’energia, ossia la capacità di un corpo di compiere lavoro. In altre parole, a ogni corpo che sta compiendo un lavoro, sotto l’azione di una forza, è associata una proprietà, che chiamiamo energia.

Ancora più semplicemente: il lavoro svolto per spostare un corpo da una posizione a un’altra rappresenta un qualcosa acquistato dal corpo, una specie di “riserva”. La forza ha trasmesso al corpo la capacità di compiere un lavoro.

Usiamo ancora qualche frase, specifica per l’energia cinetica, per cercare di chiarire al massimo il concetto: quando un corpo di massa m acquista una certa velocità o la varia per effetto di una forza,  esso acquista o varia la sua energia cinetica. Il lavoro rappresenta questa variazione di energia cinetica. L'energia cinetica è, quindi, associata alla massa e alla velocità di un corpo in movimento.

Il lavoro compiuto sulla massa si è trasformato in energia cinetica. All’istante zero e con velocità zero, il corpo non ne ha, ma alla fine del lavoro la possiede ed è proprio uguale al lavoro eseguito.

Ovviamente, se il corpo si ferma di nuovo, la sua energia cinetica torna a zero. Ha dovuto compiere un lavoro negativo e spendere l’energia che aveva acquisito.

Esiste quindi energia cinetica solo quando il corpo è in movimento. Se il movimento si effettua a velocità costante, anche l’energia cinetica rimane costante e, quindi, il corpo non compie lavoro (la forza è nulla). Questo concetto è estremamente importante e non banale come sembra. Tenetelo bene a mente.

In altre parole, ancora, l'energia cinetica di un corpo è il lavoro necessario per portarlo da una velocità iniziale a una velocità finale. Questo lavoro è immagazzinato nel corpo come energia, che rimane in attesa di essere sfruttata o cambiata in un'altra o spesa completamente.

Qualcuno dirà: “Ma il lavoro cos’è?”. Beh… ne abbiamo già parlato, ma è meglio richiamarlo in modo molto sintetico. Il lavoro è il prodotto tra la forza e lo spostamento che ha causato, nella direzione della forza. In parole povere è (in modulo):

L = F s

Ormai conosciamo gli integrali (articolo 51 e seguenti delle lezioni di matematica) e prendiamo spunto da questo richiamo per descrivere in modo formale il teorema delle forze vive o dell’energia cinetica, che dice soltanto (!) ciò che abbiamo appena detto: l'energia cinetica di un corpo è il lavoro necessario per portarlo da una velocità iniziale ad una velocità finale (il lavoro è una differenza di energia, quella finale e quella iniziale).

Consideriamo uno spostamento infinitesimo ds che comporti un lavoro infinitesimo dL

dL = F ds = (dq/dt)ds                        (non potevo dimenticare la “mia” quantità di moto…).

dL = (ds/dt) dq = v d(mv) = m vdv     ( m è costante in fisica classica…)

Integrando su un intervallo AB si ha:

L = m ∫_B^A v dv = m[v²/2] _A^B = ½ mv²_B – ½ mv²_A

Se il corpo parte da fermo, v_A = 0 e il lavoro compiuto è proprio l’energia cinetica posseduta dal corpo.

Divertiamoci con una mela

Proviamo, adesso, a lanciare una pallina (o -meglio- una mela…) verso l’alto. Per lanciarla si deve applicare una forza F alla mela e, quindi, una certa velocità v₀. Questo fatto vuol dire che al momento della partenza l’energia cinetica E_C0 della mela è:

E_C0 = ½ mv₀²

Subito dopo il lancio (la forza non agisce più) la velocità della mela è costretta a diminuire, dato che deve combattere contro la velocità di segno opposto dovuta alla forza peso. La mela, per un po’ continua a salire, ma prima o poi arriva a un’altezza h in cui si ferma. In quel momento qual è l’energia cinetica della mela? Beh, non è difficile calcolarla: dato che v = 0, anche lei deve essere uguale a zero.

Questo vuole anche dire che per passare da terra all’altezza massima la forza applicata alla mela ha svolto un certo lavoro, dato dalla differenza di energia cinetica, ossia:

L = 0 - ½ mv₀².

Un lavoro ovviamente negativo. Quale forza l’ha compiuto? L’unica presente durante il moto: la forza peso, ossia P = mg. Non per niente è negativo: lo spostamento è stato effettuato in senso opposto alla forza.

L’energia iniziale (cinetica) è stata spesa per arrivare fino ad h. A questo punto, però, la mela comincia a cadere trasportata verso il suolo, sempre dalla forza peso. Essa riacquista velocità e lo spostamento avviene nel senso della forza, che, quindi, svolge, finalmente, un lavoro positivo. Quando tocca terra qual è la velocità della mela? Proprio uguale a -v₀. Ne consegue che l’energia cinetica finale è nuovamente

E_CF = ½ m v₀²

La forza peso ha eseguito un lavoro che è dato dalla differenza tra l’energia cinetica finale (quando la mela tocca terra) e quella che aveva all’altezza h.  Ossia è adesso uguale a L = ½ m v₀² – 0.  In altre parole, il lavoro totale compiuto dalla forza peso è stato nullo. Durante tutto il percorso, inoltre, l’energia cinetica è sicuramente cambiata, ma, alla fine, è tornata quella iniziale.

Tuttavia, se è comprensibile la salita della mela in quanto possiede una certa energia di movimento alla partenza, lo è molto meno la discesa. La mela, infatti, quando passa da h al suolo, passa da un’energia cinetica uguale a zero a un’energia cinetica finale diversa da zero. Ciò vuole anche dire che la mela deve avere “creato” una qualche altra forma di energia al momento in cui ha iniziato la caduta. E questa energia non è certo di movimento, dato che la mela parte da ferma. Come per magia alla fine si è ricreata l’energia cinetica iniziale. Sarà forse merito di Maga Magò o di Mago Merlino? No,l’energia si è solo trasformata.

Ricapitolano la situazione: l’energia cinetica è sparita creando un’altra energia che nella caduta si è nuovamente trasformata in energia cinetica. In altre parole, mentre l’energia cinetica passa da un valore massimo a zero, l’altra energia passa da zero a un valore massimo. Nella discesa è avvenuto il contrario, la nuova energia torna  a zero mentre l’energia cinetica torna al valore massimo iniziale. Ma è stata proprio l’energia cinetica che ha “creato” questa nuova energia?

Assolutamente NO!

Basta prendere la mela e farla cadere da una certa altezza h. In questo caso, non esiste alcuna energia cinetica iniziale (la velocità è zero) e quindi non può essere lei a “creare” la nuova energia. Eppure esiste, dato che la mela inizia a cadere e alla fine possiede l’energia cinetica del caso precedente.

L’energia di chi sta fermo

Vedendo le cose in questo modo, possiamo dire che è stata una nuova energia a creare l’energia cinetica finale, un’energia legata solo e soltanto alla posizione del corpo, in particolar modo alla sua altezza h.

Una energia di posizione che prende il nome di energia potenziale, ossia un’energia che esiste in potenza nei corpi e che può dare origine a un lavoro. Dato che essa è sempre e comunque relativa alla forza peso, ossia alla forza di gravitazione, la possiamo chiamare energia potenziale gravitazionale e la indichiamo con U.

Riassumendo: l’energia cinetica esiste solo quando un corpo è in moto, mentre l’energia potenziale anche quando il corpo è fermo.

Facciamo attenzione che nel caso della mela che sale e scende, l’unica forza che agisce dopo il lancio è la forza di gravità (forza peso nel caso di movimenti molto piccoli vicino alla Terra, dove l’accelerazione di gravità può essere considerata costante e uguale a g). Entrambe le energie sono dovute a lei, sia quella che la fa cadere (energia potenziale), sia quella che possiede quando tocca il suolo (energia cinetica).

Quanto vale questa nuova energia in termini di gravità? Basta considerare il lavoro svolto per portare la mela da un altezza h₀ (livello del suolo) a un’altezza h . Esso è dato dal prodotto tra la forza (gm) e lo spostamento (h – h₀). Il lavoro deve essere anche uguale alla differenza di energia potenziale U tra l’istante finale e iniziale.

L =  gmh  - gmh₀ = U – U₀

Se poniamo uguale a zero l’altezza al livello del suolo, l’energia relativa vale zero e si trova:

U = gmh

Attenzione! Notate che abbiamo considerato il suolo come livello per cui h₀ = 0. Una scelta che abbiamo potuto compiere in quanto abbiamo sempre a che fare con differenze di energia potenziale (h e il suolo, oppure tra due diverse altezze). Ma anche perché g è considerata costante per le altezze dei fenomeni che stiamo trattando (mele e poco più). Dato che un corpo arrivato a terra non riesce a cadere più in basso, possiamo considerarlo come livello zero. Tuttavia, se vogliamo  allontanarci di molto dalla Terra, ossia tener conto che g è variabile con l’altezza, le cose cambiano un po’ e lo ZERO è meglio prenderlo molto, molto lontano.

Per adesso, torniamo con i piedi per… terra, dove possiamo dire che l’energia potenziale di un corpo che sta al suolo vale 0, mentre cresce andando ad altezze h.

Facciamo due conti. All’inizio della caduta la mela ha solo energia potenziale e vale U = gmh. Quando arriva in fondo la sua energia è solo cinetica e vale E_C = ½ mv². Se la portassimo in alto, invece, l’energia cinetica sparirebbe quando si ferma, ma acquisterebbe energia potenziale. Durante la caduta decresce il valore dell’energia potenziale (h decresce), mentre sale quello dell’energia cinetica (v cresce). A una certa altezza intermedia un corpo possiede sia energia cinetica che energia potenziale gravitazionale.

Tutte queste parole portano a una conclusione estremamente semplice: la somma dell’energia cinetica e di quella potenziale deve rimanere costante. Abbiamo quasi automaticamente stabilito che l’energia meccanica rimane costante, cambia solo il modo con cui si manifesta.

Liberi per sempre

Ormai sappiamo che una massa nello spazio ha una sua energia potenziale dovuta soltanto alla gravitazione della Terra o di qualsiasi corpo celeste. Attenzione, però: non confondiamo energia potenziale gravitazionale con accelerazione gravitazionale. A mano a mano che ci si allontana dalla Terra l’accelerazione di gravità diminuisce, mentre invece aumenta l’energia potenziale. Essa aumenta sempre di meno, ma aumenta, dato che trasportando un corpo sempre più in alto aumenta l’energia immagazzinata. Senza quasi volerlo ritorniamo alla definizione della velocità di fuga… che avevamo già descritto QUI (addirittura per costruirci un buco nero), ma che preferiamo scrivere di nuovo per non farvi saltellare troppo.

Cosa bisogna fare per abbandonare indefinitamente la Terra e non subirne più la forza gravitazionale? Basta imprimere alla massa una velocità che la trascini nello spazio fino a distanza infinita. Momento per momento, la velocità della massa diretta verso lo spazio diminuisce di intensità (per effetto della gravità), ma ugualmente diminuisce il rallentamento che subisce, dato che diminuisce la forza gravitazionale (e anche l’accelerazione di gravità) che cerca di opporsi al moto. L’energia cinetica diminuisce un po’ alla volta, mentre aumenta un po’ alla volta l’energia potenziale. La massa continua ad allontanarsi indefinitamente fino a raggiungere velocità zero all’infinito. Se l’energia cinetica diventa zero, tutta l’energia è energia potenziale. Essa è la massima possibile.

Ma qual è la massima energia potenziale possibile? Non dobbiamo farci ingannare dagli esperimenti fatti con la mela. In quel caso abbiamo considerato l’accelerazione di gravità costante e abbiamo scelto il livello del suolo come altezza zero, dove considerare nulla l’energia potenziale.

Queste scelte non hanno creato problemi dato che si lavorava sempre con differenze di energie e ad altezze ridicole rispetto al suolo terrestre. La scelta del livello zero per quella potenziale era quindi del tutto arbitraria. In altre parole, abbiamo studiato il moto in un ambito estremamente ristretto, ma più che sensato per qualche mela o qualche pallina.

Adesso, però, vogliamo andare ad altezze estremamente più grandi del raggio terrestre. Non possiamo più considerare l’accelerazione di gravità g come una costante. Dobbiamo tenere conto che essa varia seguendo la legge di gravitazione universale e non con la forza peso che è solo una sua approssimazione nei pressi della superficie terrestre. Per far ciò dobbiamo considerare la massa della Terra concentrata in un punto e pensare che quando un corpo si trova al suolo esso è comunque soggetto alla gravità della massa terrestre che gli sta “sotto”. In altre parole, la sua energia potenziale al suolo non può essere considerata zero come prima, ma ha un valore ben definito che dipende dal raggio della Terra.

L’accelerazione di gravità è:

g = GM/r²

come si vede essa non è assolutamente costante, ma diminuisce velocemente al crescere della distanza r dal centro della Terra di massa M (dove, come già detto, si può immaginare di concentrare tutta la massa).

Quanto vale allora l’energia potenziale al suolo, ossia a una distanza R dal centro della Terra? Facile a scriversi:

U = mgR = m GM/R

Tuttavia, qual è il segno di questa energia? Noi l’avevamo considerata zero e avevamo considerate positive quelle ad altezze maggiori. Nessun problema in quanto g era costante e potevamo scegliere a piacere il livello zero. Ora non possiamo più farlo, dato che sappiamo che g dipende dalla distanza dal centro della Terra.

Il valore minimo dell’energia deve essere quello raggiunto al centro della Terra. E’ lì che la distanza è uguale a zero. Ma se r = 0, l’energia tende a essere infinita, dato che il raggio compare al denominatore. Dividendo per un numero sempre più piccolo, sappiamo benissimo che la grandezza deve tendere a infinito. L’infinito sembra un numero molto grande e non piccolo. Accidenti, come possiamo avere un numero infinito, ma piccolissimo? Banale. Lo otteniamo solo se il suo valore è sempre negativo.

Deve essere allora:

U =  - GmM/r    …. (1)

Non era difficile capirlo fin dall’inizio. Quando si porta un corpo dal centro della Terra fino a un’altezza R (uguale al raggio, ossia fino alla superficie terrestre) il lavoro è negativo, in quanto è contrario al verso della forza di attrazione gravitazionale. Ma se il lavoro è negativo vuol dire che la differenza di energia deve essere negativa.

Possiamo perciò concludere che se la distanza di un corpo di massa m dalla superficie terrestre (o di qualunque altro corpo celeste) è tale da non poter trascurare le variazioni della forza gravitazionale con la distanza, allora l'energia potenziale ad una distanza r dal centro del corpo celeste è definita da una quantità sempre negativa, il cui “valore assoluto” (la parte positiva) decresce all’allontanarsi dal centro, in modo che cresca il valore dell’energia. Una quantità negativa che diventa più piccola aumenta il suo valore.

Qual è il valore massimo dell’energia potenziale? Essendo sempre negativa raggiunge il suo valore massimo quando arriva a zero. Come fa a diventare zero? Basta che la distanza r dal centro della Terra diventi infinita. Più è grande il denominatore della (1) è più piccola, in valore assoluto, è l’energia e quindi più grande il suo valore negativo.

Cosa ne consegue? Che la massa m deve essere lanciata a una velocità tale da raggiungere un valore di energia potenziale massima (uguale a zero) proprio all’infinito. Come arriverà in quel punto la nostra massa? La sua velocità è diventata zero, ossia è diventata zero anche la sua energia cinetica. L’energia meccanica totale della pietra in queste condizioni deve perciò essere uguale a zero (0 + 0 = 0).

Per la conservazione dell’energia deve perciò sempre valere:

E_C + U = 0

Questa relazione deve essere valida anche al momento del lancio. L’energia cinetica deve quindi essere uguale e contraria a quella potenziale posseduta dalla massa e che dipende solo dalla distanza r dal centro della Terra. Solo così si ottengono sia la condizione all’infinito (annullamento dell’energia meccanica totale) che la conservazione dell’energia meccanica totale.

½ mv₀² = GmM/r       ….  (2)

Dalla (2) si ottiene subito la velocità necessaria per allontanarsi indefinitamente dalla gravitazione terrestre e raggiungere velocità zero all’infinito. Se r = R (raggio della Terra), ossia se la massa m viene lanciata dalla superficie terrestre, la velocità viene chiamata velocità di fuga e indicata con v_f. Essa si ricava subito dalla(2), dove tutte le grandezze sono note tranne proprio la velocità.

v_f² = (2GM/R)

e infine:

v_f = (2GM/R)^½  …. (3)

Nel caso della superficie terrestre essa vale 11.2 km/s.

Lo so, lo so, ho ripetuto cose già ben note, ma quando si entra nel mondo della meccanica i concetti diventano ciliegine e uno tira l’altro…  La parte precedente può quindi essere saltata da chi conosce bene la meccanica elementare, ma è pur sempre un richiamo che può essere utile avere sotto mano.

Quanto detto per la Terra vale per qualsiasi altro oggetto celeste: basta cambiare la massa M. La (3) ci dice, però, anche un’altra cosa molto importante (che già dovremmo sapere): la velocità di fuga non dipende dalla massa dell’oggetto. Per mandare nello spazio infinito una pietra o un’astronave mostruosamente grande la velocità necessaria è la stessa (cambia solo la forza necessaria). D’altra parte, anche la velocità di caduta sulla Terra dall’infinito (in assenza di altre masse attrattive) è indipendente dalla massa del corpo, come già Galileo si era sforzato di dimostrare.

Abbiamo capito che a parità di distanza dal ragno centrale, l’energia potenziale gravitazionale ha un certo valore. Se ci allontaniamo cambia in relazione all’altezza. In parole povere esistono superfici (in questo caso più o meno simili a superfici sferiche, in quanto la Terra è quasi una sfera) che hanno la stessa energia potenziale. Ed ecco che abbiamo creato una nuova ragnatela… una ragnatela energetica.

Una nuova ragnatela

E se invece di avere solo la Terra, avessimo due corpi molto massicci? Le curve di energia potenziale costante non sarebbero più sfere, ma superfici più complesse.  In altre parole, arriviamo, finalmente, al caso delle superfici equipotenziali attorno a sistemi stellari doppi e alla definizione di lobi di Roche e di punti lagrangiani in sistemi rotanti.

Dobbiamo, prima, introdurre (abbiate pazienza) alcuni concetti, che non ci sono del tutto nuovi, ma che meritano di essere trattati con maggiore attenzione.

Torniamo alla stella singola e riprendiamo in mano l’energia potenziale. Essa non è altro che il lavoro compiuto da una massa m (la nostra mosca caduta nella ragnatela) per passare da una certa distanza A a una distanza B rispetto alla massa della stella-ragno M (Fig.3).

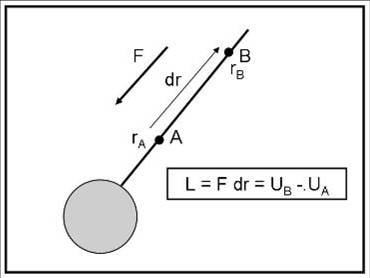
Il lavoro per passare da A a B può essere scritto:

L =  F dr = U_B – U_A = ∫_B^A GmM/r =  GMm (1/r_A – 1/r_B)

Ripetiamoci, dato che non fa mai male: si definisce come energia potenziale di un punto P, a distanza r dal centro della stella (il suo baricentro), la grandezza:

Ur = - GmM/r

Il segno meno sta a indicare che questa energia è sempre negativa (il lavoro per andare verso lo spazio è negativo, dato che ci si muove in verso opposto alla forza di gravità).

L’energia potenziale gravitazionale raggiunge il suo valore massimo, ossia zero, proprio all’infinito. Solo in quel punto ipotetico è massima l’energia immagazzinata. Ripeto ancora: non confondiamola con l’accelerazione di gravità che tende a zero in quanto raggiunge il suo valore minimo. L’equazione è quella di un ramo di iperbole e quindi può essere facilmente tracciata nella Fig. 4.

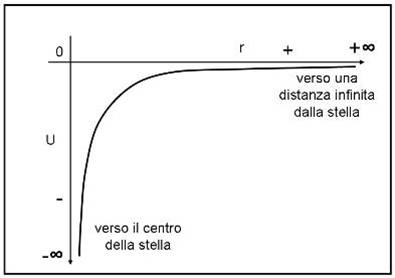
Ricordiamoci bene, ancora una volta, questi concetti: l’energia potenziale in un campo gravitazionale è sempre negativa e cresce al crescere della distanza dal baricentro della massa della stella. Mentre l’accelerazione gravitazionale diventa sempre meno intensa, l’energia potenziale aumenta. D’altra parte è ovvio: per arrivare a una distanza infinita si deve fare più lavoro che per giungere a poche migliaia di chilometri!

La formula:

U = - GMm/r

ci regala una grandezza importantissima, ma, ancora una volta, contiene la massa m dell’astronave o del corpo che abbiamo usato per definirla nell’intorno della stella. Agiamo come fatto per il campo gravitazionale e dividiamo entrambi i membri per la massa m. Otteniamo:

Q = U/m = - GM/r

Questa grandezza prende il nome di potenziale ed è indipendente dalla massa dell’oggetto caduto nella rete. Essa dipende solo dalla massa della stella-ragno e dalla distanza rispetto al suo baricentro.

Fissiamoci bene in testa la differenza tra energia potenziale e potenziale. La prima è il lavoro che si deve fornire alla massa m per portarla fino all’infinito, la seconda è invece il lavoro che è necessario fornire alla massa m unitaria per portarla fuori dal campo (cioè a distanza infinita). La differenza è enorme anche se non sembra! Nel primo caso in un certo punto P dello spazio potremmo avere tanti valori di energia, dato che dipende dalla massa; nel secondo caso vi è invece un valore unico, indipendente dalla massa del corpo che va a occuparlo.

Nel campo gravitazionale (anch’esso indipendente dalla massa) è allora possibile disegnare delle curve molto speciali che rappresentano il luogo dei punti aventi lo stesso potenziale, ossia le curve equipotenziali. La nostra mappa si arricchisce.

Nel caso di una stella singola il campo gravitazionale è definito dalle linee di forza che convergono verso il centro. Le curve equipotenziali devono allora essere delle circonferenze che si allargano sempre più andando verso l’esterno. Il potenziale, infatti, dipende solo dalla distanza dal centro della stella (la massa è sempre la stessa).

E’ ovvio che le curve equipotenziali sono proprio quelle in cui la distanza dal centro della stella è costante. La curva che ha queste caratteristiche è proprio la circonferenza che ha per centro il baricentro della stella. Ne consegue anche che la tangente in un punto P della circonferenza (linea equipotenziale) è sempre perpendicolare alla retta passante per il centro e per quel punto. In altre parole la tangente punto per punto di una linea equipotenziale è perpendicolare alle linee di forza che definiscono il campo gravitazionale. La Fig. 5 spiega la situazione molto meglio di tante parole.

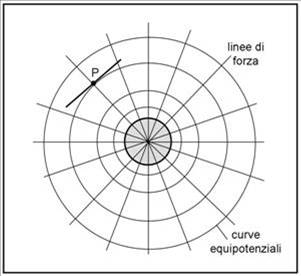
Ovviamente, noi abbiamo parlato di linee equipotenziali, perché disegniamo tutto su un piano. In realtà esse sono superfici sferiche di raggio crescente. Anche il campo gravitazionale si estende a tutto lo spazio a tre dimensioni attorno alla stella. La Fig. 5 è quindi una sezione piana di una mappa a tre dimensioni.

Raddoppiamo la nuova ragnatela

Vediamo come si trasformano le curve equipotenziali in un sistema doppio di stelle? Non è difficile immaginarselo, dato che esse devono sempre essere perpendicolari alle linee di forza. E le linee di forza di un sistema doppio le avevamo già viste nel campo gravitazionale.

La Fig. 6 schematizza molto qualitativamente la situazione.

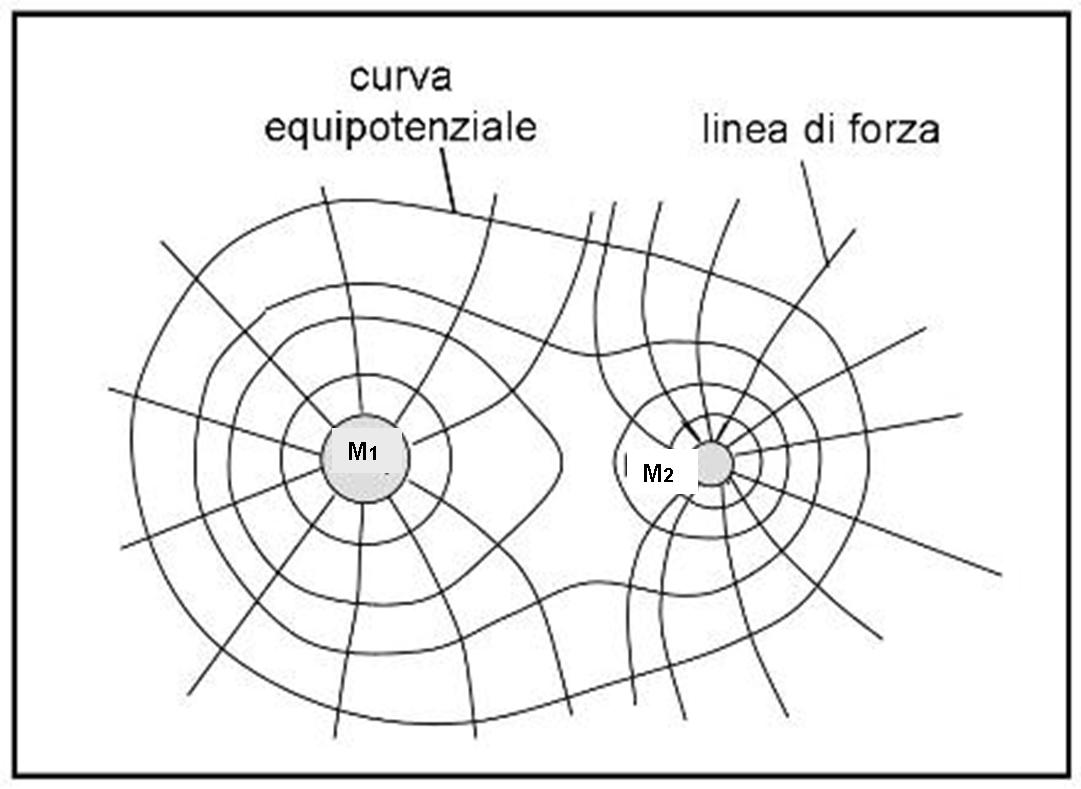
E’ proprio attraverso lo studio delle superfici equipotenziali che si possono stabilire i limiti di crescita delle singole stelle, il momento in cui inizia il trasferimento di massa e molte altre cose. Cerchiamo di descrivere la situazione limitandoci, ovviamente, ai concetti essenziali e tralasciando le formule più complicate.

Il potenziale totale

Consideriamo un sistema formato da due stelle che rivolvano entrambe attorno al proprio baricentro, come quello rappresentato in Fig. 7.

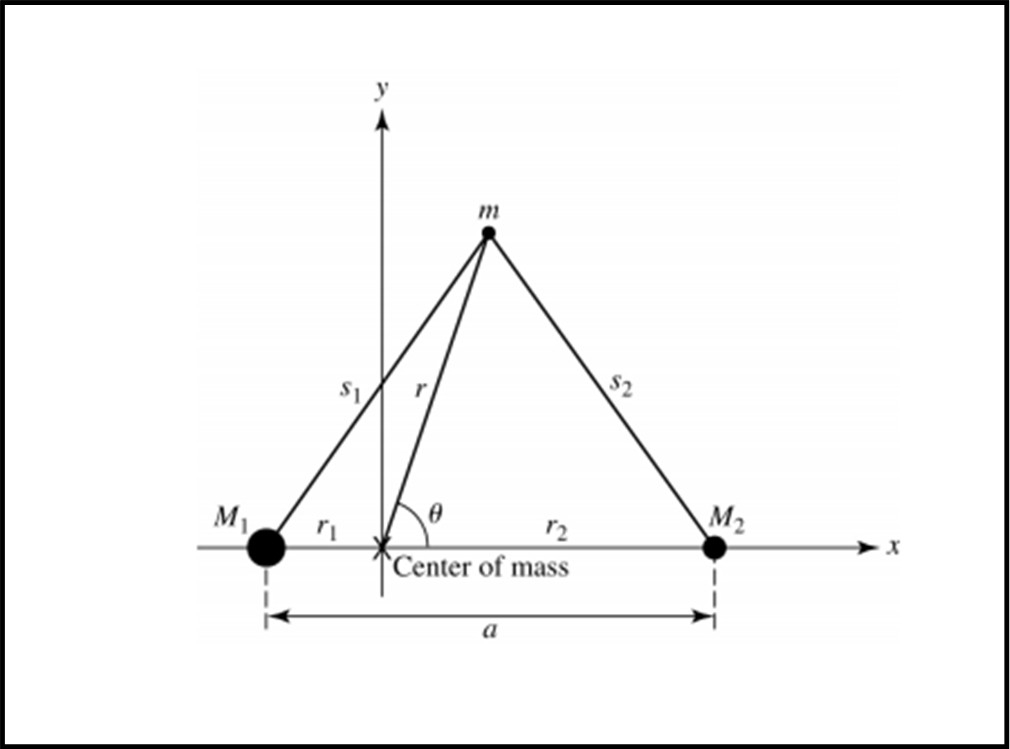
Il potenziale di un punto immerso nel campo gravitazionale del sistema è dato, come ormai sappiamo, dalla somma dei potenziali delle singole stelle

Q = - GM₁/s₁ - GM₂/s₂

A questo punto, immaginiamo di entrare nel sistema rotante e di mantenere fisso l’asse che congiunge le stelle (cosa che abbiamo già fatto spesso), prendendo come origine il baricentro del sistema (ma non è obbligatorio, l’importante è che si sia solidale con la rotazione).

Le condizioni di equilibrio di un punto devono, allora, anche tener conto della forza centrifuga. Al potenziale gravitazionale bisogna allora aggiungere anche il potenziale della forza centrifuga.

La forza centrifuga agente sulla massa m è data da:

F_C = m ω²r

Per calcolarne l'energia potenziale sarebbe più "fine" usare la Lagrangiana (chissà... un giorno), ma possiamo lavorare in termini di energia potenziale, sapendo che la forza (in questo caso centrifuga) può essere espressa come:

F_C = - dU_C/dr         (la variazione dell’energia è proprio la forza moltiplicata per la variazione di r)

La differenza di energia potenziale, ossia il lavoro, relativa a questa forza è data da:

ΔUc = - ∫₀^r m ω²r dr = - [1/2 m ω²r²]₀^r =  - 1/2m ω²r² + 0

Avendo posto l’energia uguale a zero per r uguale a zero.

Dividiamo per m e otteniamo il potenziale centrifugo:

Qc =  -1/2 ω²r²

In conclusione, il potenziale totale risulta:

Φ = - GM₁/s₁ - GM₂/s₂ - 1/2 ω²r²

L’intersezione delle superfici di uguale potenziale con il piano orbitale è dato dalla Fig. 8, che conosciamo molto bene. In essa sono anche segnati i punti lagrangiani, che sono i punti in cui  la forza gravitazionale è esattamente uguale alla forza centripeta necessaria a farli ruotare con la velocità angolare ω, ossia a restare fissi nel sistema rotante. Ma ci torneremo ancora sopra, alla fine.

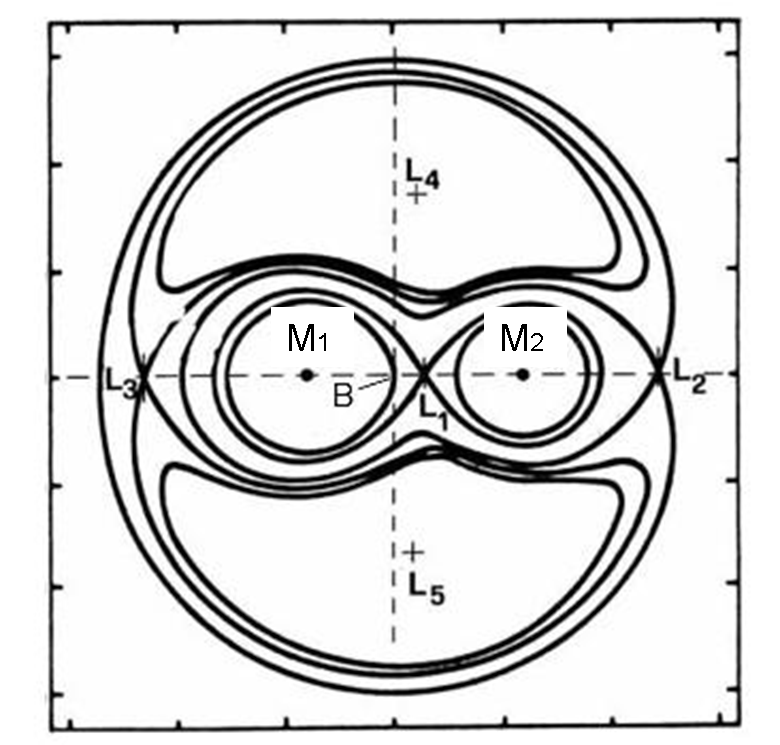
L’analisi della Fig. 7 porta alle seguenti relazioni (ricordando il teorema di Carnot):

s₁² = r₁² + r² + 2r₁r cos(ϑ)

s₂² = r₂² + r² - 2r₂r cos(ϑ)

mentre la legge di Newton permette di scrivere:

ω² = (2π/P)² = G (M₁ + M₂)/a³

Le ultime quattro relazioni permettono, fatti i dovuti passaggi, di calcolare il potenziale totale in ogni punto del piano orbitale delle due stelle di massa M₁ e M₂.

Come esempio più che significativo, consideriamo soltanto la componente della forza che agisce sulla nostra particella di massa m lungo l’asse x. La forza non è altro che la derivata del potenziale rispetto a uno spostamento dx, per cui è sufficiente trovare gli zeri di dΦ/dx. Normalizzando adeguatamente la funzione Φ, in relazione alle masse in gioco e alla loro distanza, si ottiene il grafico di Fig. 9.

I massimi della funzione sono i punti lagrangiani L1, L2 e L3, proprio quelli dove la tangente alla curva potenziale è orizzontale (derivata nulla: le derivate sono spiegate nell’articolo 23 e seguenti delle lezioni di matematica). In corrispondenza delle due stelle abbiamo invece i punti di minimo potenziale. I punti in cui si annulla la derivata sono i punti in cui si annulla la forza agente su di loro e quindi punti fermi nel sistema rotante con le due stelle. Possiamo proprio chiamarli buchi di potenziale.

Le stelle doppie strette: Ragni e prede nello stesso tempo

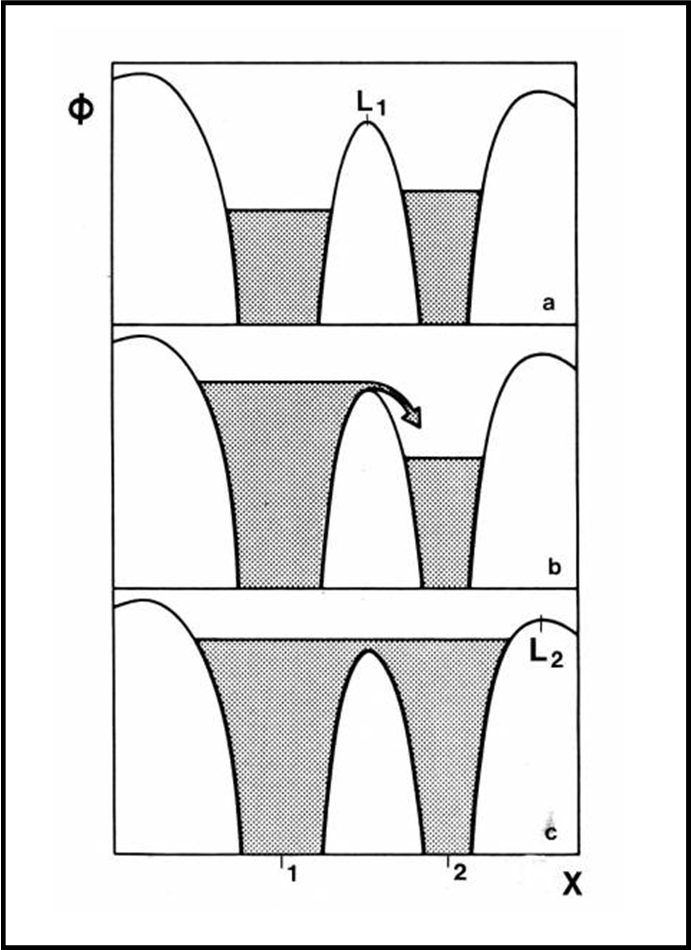
La Fig. 9 vale per qualsiasi particella, anche per quelle che appartengono alle due stelle “fisiche”, che nella trattazione precedente abbiamo considerato puntiformi. In altre parole le stelle reali si sistemano all’interno dei due minimi di potenziale, riempiendo un po’ alla volta tutto “il buco” compreso tra i vari massimi. Immaginiamo quindi, di vedere il profilo di Fig. 9, come una serie di colline in cui continua a cadere pioggia che riempie sempre di più i buchi. Ovviamente, la “pioggia” è la materia stessa delle due stelle. La materia stellare aumenta il proprio volume (non la massa, per adesso) fino a colmare il buco più basso (relativo alla collina L1) e può passare da uno all’altro dei buchi stellari originali. Attraverso quel solo punto, L1, le stelle possono svolgere i loro giochi di travaso di materia.

L2 e L3 vengono usati quando entrambe le stelle (diventate praticamente una sola utilizzando il punto L1) arrivano al limite delle colline esterne. La materia può uscire nello spazio circostante (binarie a inviluppo unico).

Ovviamente, è ormai chiaro a tutti che i buchi di potenziale rappresentano i lobi di Roche.

Ricapitolando: Una stella, durante la sua evoluzione, aumenta il diametro fino a riempire completamente il suo lobo di Roche. La materia stellare deve trovare una via d’uscita e questa è proprio offerta da L₁. Basta una piccola spintarella data dal vento stellare e la materia oltrepassa quel punto di equilibrio instabile e inizia a cadere verso la compagna. L₂ e L₃ ci dicono, invece, che quando le stelle riempiono entrambi i lobi di Roche, la materia può sfuggire verso l’esterno, attraverso di loro.

Torniamo alla Fig. 8, con maggiore conoscenza della situazione e ripetiamo ancora una volta certi concetti in modo leggermente diverso, ma altrettanto esplicativo. Se siete arrivati alla “noia”, benissimo! Vuol dire che avete capito perfettamente una configurazione fondamentale per l’evoluzione stellare delle stelle doppie strette (ricordiamo che sono proprio loro che portano alle supernove di tipo Ia).

Le linee equipotenziali ci dicono, in generale, che se stiamo vicini alle stelle, il campo che domina è quello gravitazionale, mentre se si va verso l’esterno prende il sopravvento quello centrifugo.  Nei dintorni delle due masse stellari le superfici dipendono solo dalla massa più vicina e sono molto simili a circonferenze (leggermente deformate per effetto della seconda massa). A un certa distanza dalle stelle, la superficie equipotenziale diventa una specie di otto. Il punto L₁ è quindi estremamente “imbarazzato”. Si trova proprio in mezzo ai due giganti. Un oggetto posto in quella posizione rimane in equilibrio, ossia rimane immobile rispetto alle due stelle che nel sistema rotante sono fisse per definizione (QUI abbiamo descritto cosa vede un satellite artificiale in orbita in L1). In altre parole, ruota solidalmente con loro. Non confondiamo il punto lagrangiano L₁ con il baricentro! Sono due cose completamente diverse.

In parole veramente povere, potremmo dire che in quella posizione l’attrazione gravitazionale di M₂ cancella parzialmente quella di M₁. Tuttavia, per i più smaliziati questa considerazione può non bastare. Infatti, qualcuno potrebbe dire: “Se M₂ sta ferma, come può stare fermo un punto che è più vicino di lei a M₁? Il suo periodo di rotazione attorno a M₁ dovrebbe essere più breve. In altre parole, il punto dovrebbe muoversi rispetto al sistema che mantiene fissa la direzione M1- M2.”

Ciò sarebbe vero se non ci fosse M₂. Questa, nel suo piccolo, sottrae un po’ di forza centripeta all’oggetto “imbarazzato” e gli rallenta il periodo di rivoluzione facendolo diventare uguale al suo. E quindi NON lo fa ruotare nel sistema rotante della figura.

Gli altri punti di equilibrio sono meno intuitivi. L₂ si trova dalla parte opposta di M₂ rispetto a L₁. Ciò che capita in quel punto è che la forza centrifuga eguaglia perfettamente quella gravitazionale dovuta a M₁ e M₂. Anch’esso allora ruota solidalmente con il sistema rotante, ossia rimane fermo rispetto alle due masse. L₃ è l’analogo di L₂, dalla parte opposta del sistema (vedi anche QUI).

I punti L₄ e L₅ sono, invece,  più interessanti da un punto di vista dinamico. Essi si trovano nel terzo vertice dei due triangoli equilateri che hanno come altri due vertici le masse M₁ e M₂. Come mai sono in equilibrio? L’abbiamo già trattato ampiamente (QUI).

Ribadiamo il concetto in modo sintetico: avendo distanza uguale rispetto alle due masse, essi subiscono attrazioni gravitazionali che dipendono soltanto dalle masse delle due stelle. In altre parole, il rapporto tra le forze gravitazionali che subiscono è uguale al rapporto delle masse. Queste condizioni fanno sì che la risultante delle due forze passi esattamente per il baricentro del sistema rotante. Di conseguenza non causa alcuna rotazione supplementare ed essi rimangono fissi nel sistema solidale con le due masse.

Spero, con questo lungo articolo che ha sconfinato nella fisica classica elementare, di aver aiutato a sciogliere molti dubbi e non di aver fatto maggiore confusione. Comunque, sono qui per chiarire e modificare –se necessario-. Il nostro è un circolo fondato sulla collaborazione!