Questo articolo fa parte di una piccola serie dedicata ad un approfondimento sui metodi che abbiamo utilizzato per risolvere il quiz proposto da Enzo qui.

In particolare, questa parte è dedicata all’applicazione del metodo di Lagrange. L’articolo dovrebbe essere accessibile anche a chi non conosce questo metodo. Per questo accompagno l’applicazione del metodo con una sua breve descrizione.

Chi ha avuto la pazienza di leggere la mia serie di articoli sulla Lagrangiana, potrà trovare qui un'applicazione del metodo ad un caso interessante con un riepilogo ed una integrazione degli argomenti trattati negli articoli.

Nel seguito troverete questi argomenti:
La descrizione del sistema meccanico che vogliamo analizzare
Breve introduzione al metodo di Lagrange
Il riferimento e le coordinate: il momento delle scelte
Anticipo del risultato: in quale verso si muovono il cuneo ed il cubo?
Applicazione del metodo di Lagrange: troviamo la Lagrangiana del nostro sistema
Dalla Lagrangiana alle leggi orarie: le equazioni di Eulero-Lagrange

Passiamo al nostro problema.

Ricapitolo in cosa consiste il sistema meccanico che vogliamo analizzare.

Abbiamo un cuneo triangolare di massa M appoggiato su un piano orizzontale sul quale può scorrere senza attrito. Il piano del cuneo è inclinato di un angolo α rispetto al piano orizzontale.

Sul cuneo è appoggiato un cubo di masso m. Il cubo può scorrere senza attrito sul piano inclinato del cuneo. Al cuneo è applicata una forza orizzontale costante F (non era presente nel quiz). Il cuneo ed il cubo sono soggetti alla forza di gravità. L’intero sistema è collocato in una zona dove possiamo assumere che l’accelerazione di gravità sia costante. Vogliamo trovare cosa accede al cubo ed al cuneo, inizialmente bloccati, quando vengono rilasciati. In particolare siamo interessati al verso dei loro movimenti.

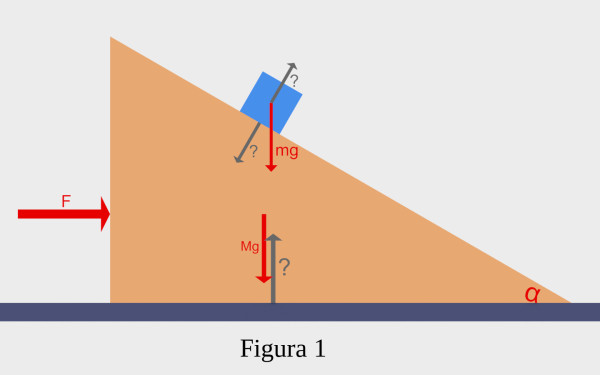
Nella figura rappresento graficamente quanto detto sopra. Le forze attive in gioco sono rappresentate in rosso. Ci sono le forze dovute alla gravità. Queste forza si applicano al cubo (mg) ed al cuneo (Mg). L’intensità delle forze è quella vicina alla superficie terrestre. Inoltre c’è la forza esterna F che è applicata al cuneo.

Oltre alle forze attive ci sono le forze di reazione dei vincoli, rappresentate in grigio: quella del piano orizzontale sul cuneo e quella del cuneo sul cubo e viceversa. L’affermazione riguardo l’assenza di attrito comporta che le forze di reazione siano perpendicolari alla superficie dei due vincoli. Le intensità di queste forze di reazione non sono note a priori.

Lagrange scoprì che il testo che descrive il sistema che abbiamo letto sopra può essere trasformato in una espressione matematica. Una singola espressione matematica che contiene tutti gli elementi necessari per risolvere il problema. Questa espressione è chiamata funzione Lagrangiana.

La Lagrangiana dei sistemi meccanici si ottiene dalla sottrazione dell’espressione dell’energia potenziale (U) dell’intero sistema all’espressione dell’energia cinetica (K) dell’intero sistema.

L=K-U

Il termine U contiene le informazioni sulle forze che agiscono sul sistema. Queste forze debbono essere associabili ad un potenziale. Vedremo che le forze attive di figura 1 sono di questo tipo. Normalmente ciascuna forza che agisce sul sistema è rappresentata da un termine aggiuntivo in U. Forze dovute all'attrito, che non sono associabili ad un potenziale,  non possono essere espresse in questa forma. Per molte applicazioni l'assenza di attrito può essere una condizione accettabile, in particolare nella fisica fondamentale dove l'attrito non c'è. Il termine K dipende solo dalla configurazione del sistema e non dalle forze.

Nel nostro caso, ad esempio, se volessimo studiare il comportamento del sistema in figura 1 in assenza di forze avremmo il solo termine K. Se aggiungiamo la gravità che agisce sul cuneo e sul cubo, a quel termine K si aggiunge un termine U con due elementi. Se aggiungiamo anche le forza F, che agisce sul cuneo, abbiamo un ulteriore elemento in U. Se avessimo ulteriori forze, es. elettriche,  queste aggiungerebbero altri elementi in U.

Lagrange scoprì anche come ricavare da questa funzione tutte le informazioni sul moto del sistema.

Le regole per costruire la Lagrangiana e per poi ricavarne le informazioni sul moto degli elementi del sistema formano il metodo di Lagrange per la risoluzioni dei problemi meccanici e non solo.

Il sistema Cuneo-Cubo è molto adatto per mettere in evidenza le caratteristiche del metodo di Lagrange. In particolar modo in questa occasione che ci permette di mettere a confronto ravvicinato un procedimento che segue il metodo “Newtoniano” con un procedimento che segue il metodo di Lagrange. Vedremo che l'applicazione di questo metodo richiede una sequenza di elaborazioni in gran parte predefinita. Non necessita di ragionamenti affidati alla nostra intuizione geometrica. Per contro, gli sviluppi algebrici e analitici possono presentarsi non del tutto agevoli, almeno le prime volte che si affrontano.

Ora costruiamo l’espressione della Lagrangiana del nostro sistema: L=K-U.

Partiamo dall’energia cinetica.

L’energia cinetica di ciascun elemento è espressa dalla solita formula . Nel nostro sistema il cuneo e il cubo non ruotano, altrimenti dovremmo aggiungere altri termini.

La velocità, e quindi l’energia cinetica, è una grandezza che dipende dal sistema di riferimento che scegliamo di utilizzare per esprimerla. Inoltre l’espressione  è direttamente utilizzabile solo per riferimenti inerziali.

Questo è il momento delle scelte.

Qui viene naturale scegliere come sistema di riferimento quello del piano di base. Quello dove cuneo e cubo sono inizialmente fermi. Questa scelta è tanto naturale che probabilmente l’abbiamo già fatta senza esplicitarla quando abbiamo iniziato a pensare al problema.

Certamente sarebbero possibili scelte diverse, ma dovrebbero essere comunque riferimenti inerziali. Ad esempio non va bene un riferimento solidale al cuneo o al cubo perché vedremo che non sono inerziali (si muovono di moto accelerato) e, comunque, non possiamo garantire inizialmente che siano inerziali. Rimaniamo quindi sulla scelta fatta. Utilizziamo come riferimento quello fermo rispetto al piano di base.

Per esprimere l’energia cinetica occorre anche scegliere le coordinate che utilizzeremo. Sembrerebbe una scelta direttamente conseguente a quella precedente, ma non lo è. Lagrange qui ci da’ molta libertà. Vedremo come utilizzarla.

In pratica ci impone solo due condizioni. Il numero di coordinate che scegliamo di utilizzare deve essere il minimo indispensabile necessario per descrivere la configurazione del sistema. Qualsiasi sia la scelta fatta dobbiamo poi esprimere K nel sistema di riferimento inerziale scelto. Per il resto possiamo scegliere praticamente qualsiasi coordinata, anche non inerziale. Sembra una contraddizione con quanto detto per il riferimento. Vedremo in pratica che non lo è. In realtà, in alcuni problemi può essere un elemento di flessibilità utile per rendere il problema matematicamente più abbordabile.

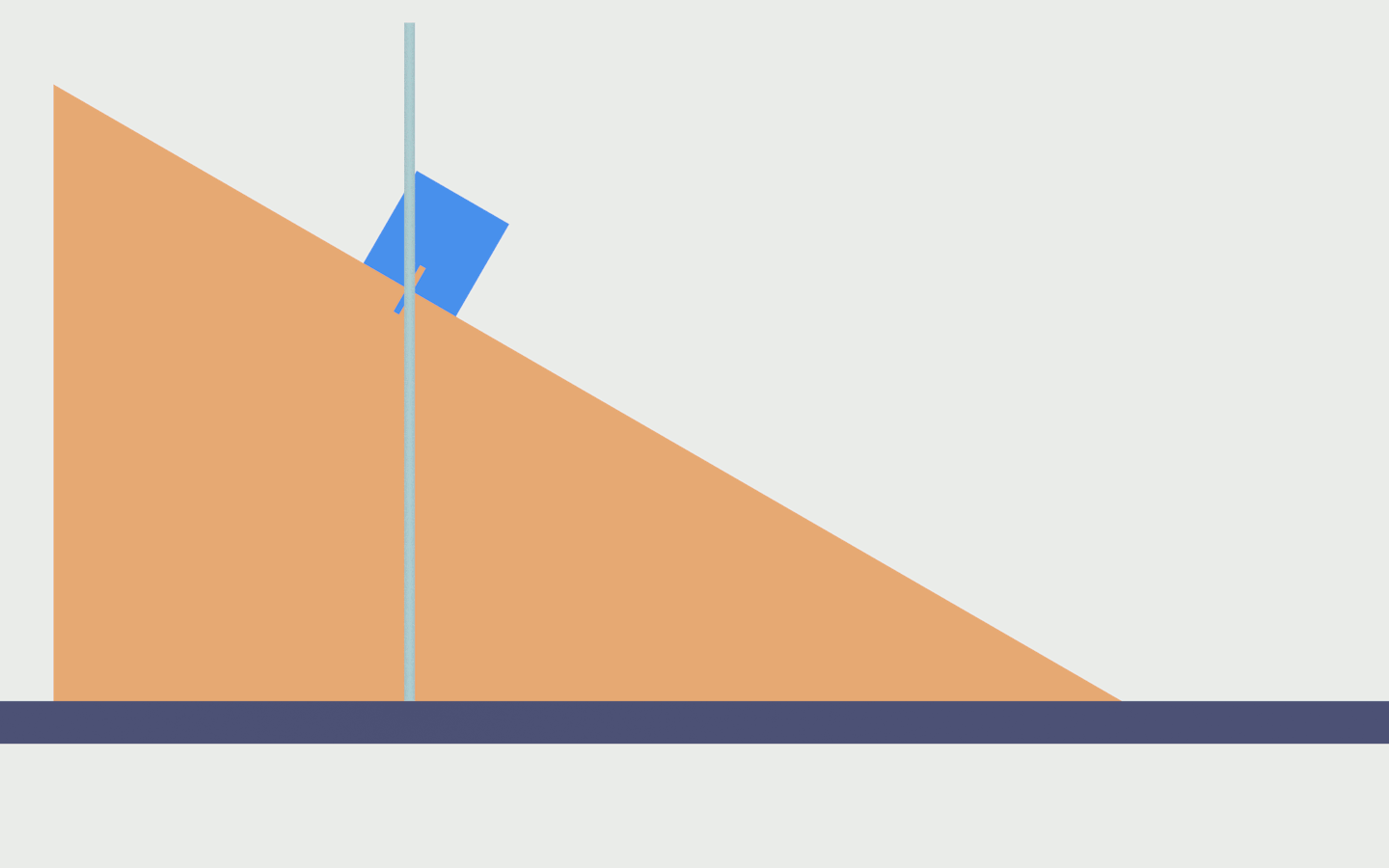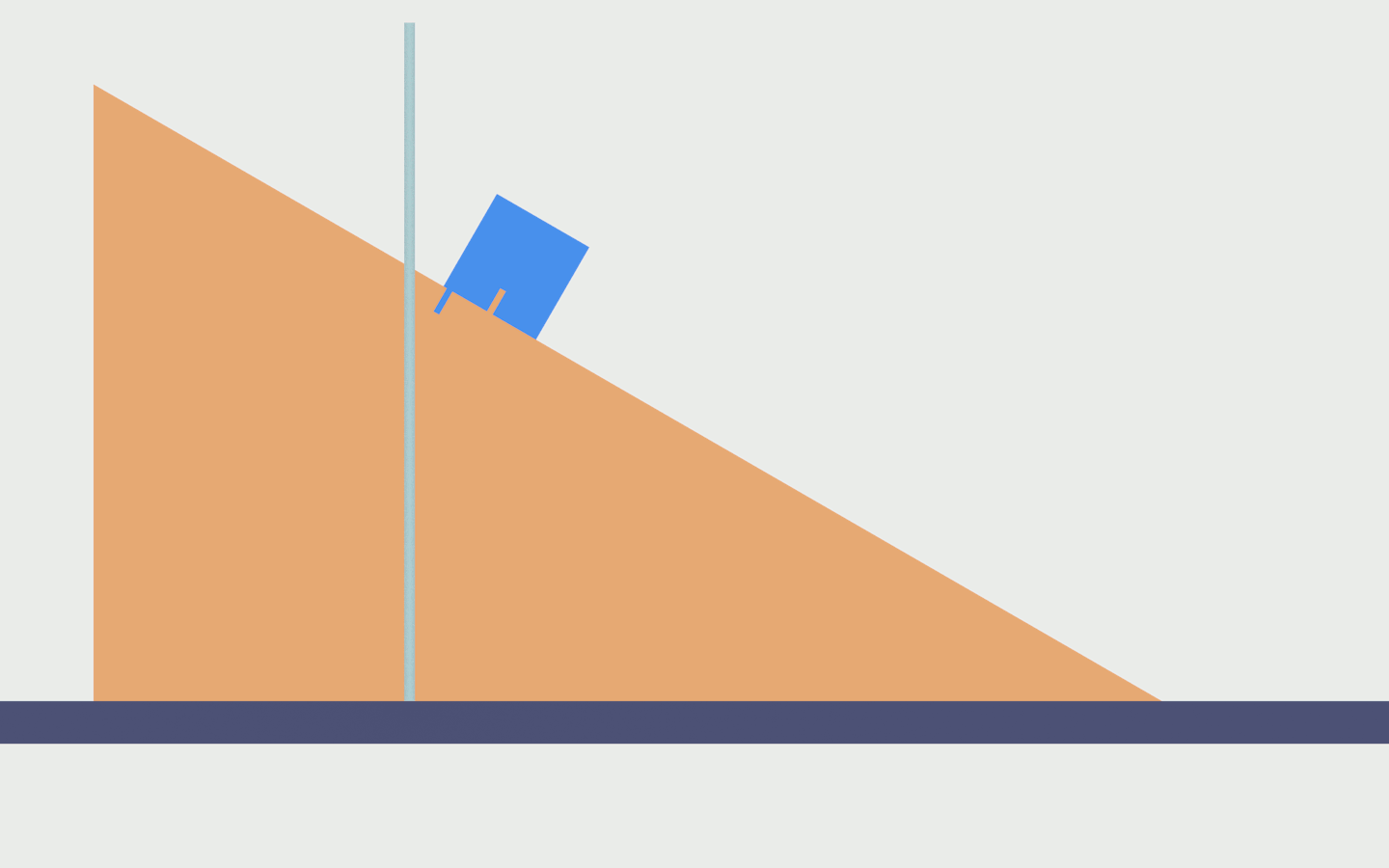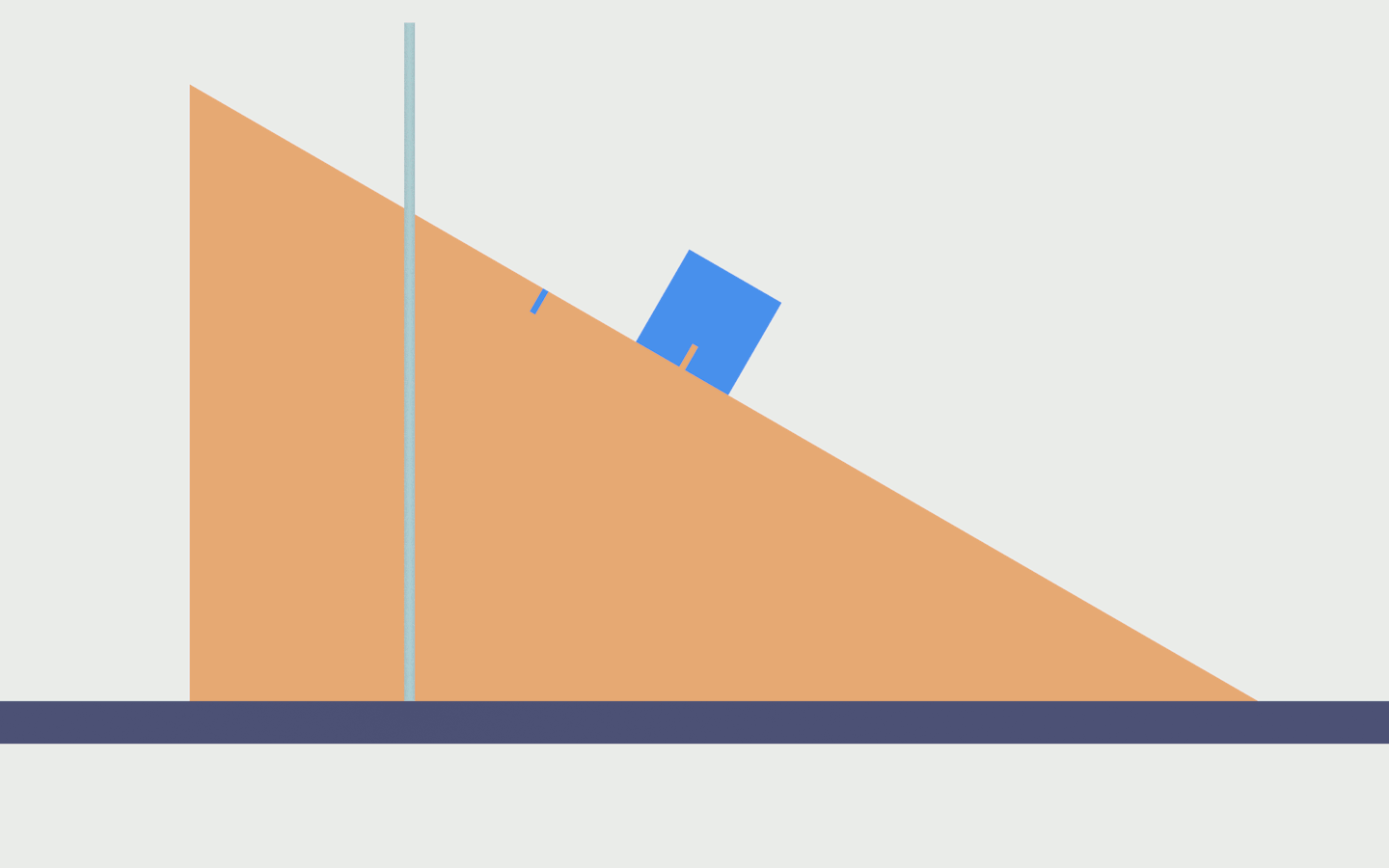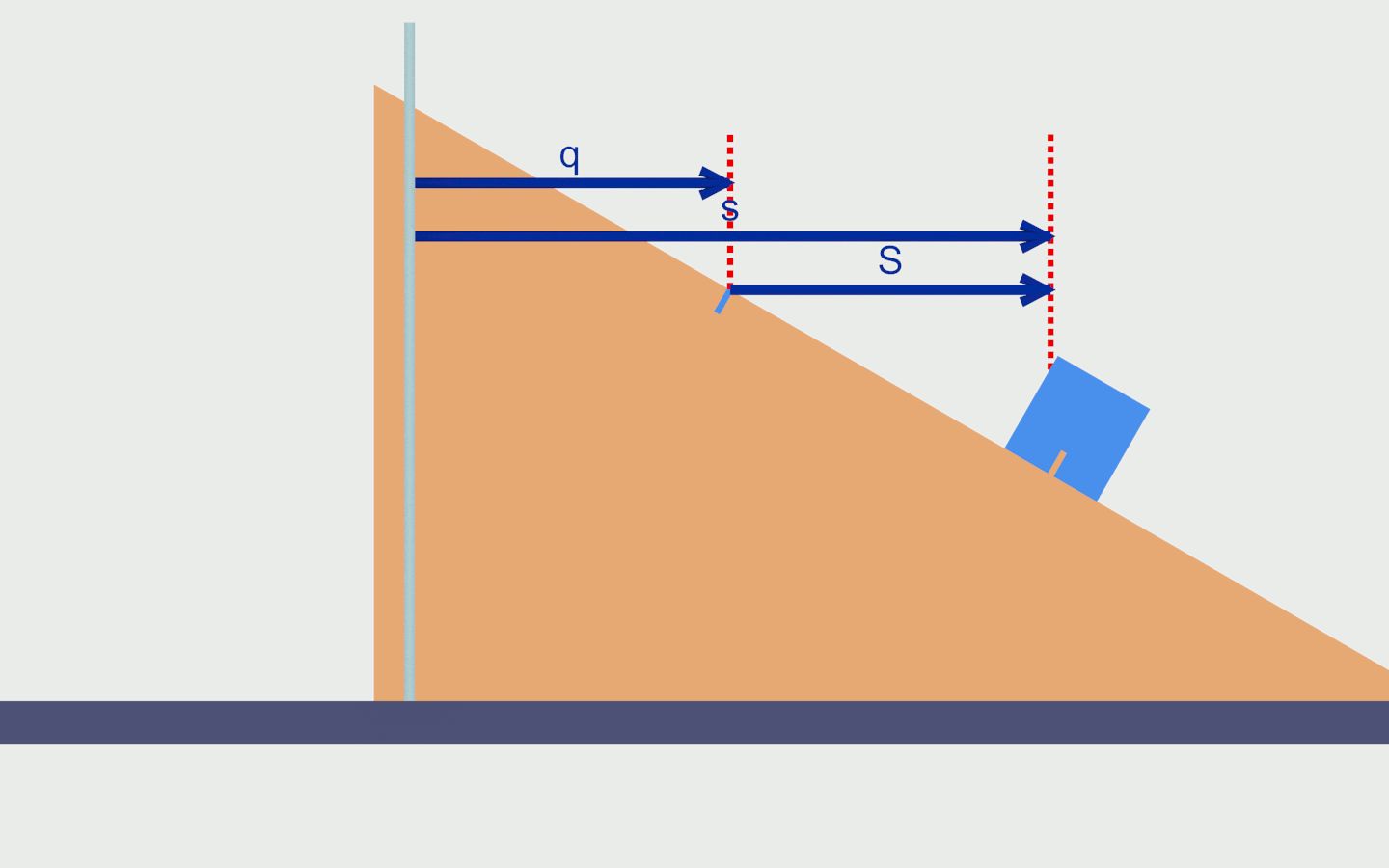
Nel nostro sistema ci sono due oggetti. Il cuneo che può muoversi solo orizzontalmente. Il cubo che si muove sia in orizzontale sia in verticale. Per i movimenti orizzontali, viene naturale scegliere delle coordinate che ci dicano di quanto il cuneo ed il cubo si sono spostati orizzontalmente. Ad esempio, segno con un picchetto ancorato alla base il punto dove si trova inizialmente il cubo. Ci segnerà l’origine delle coordinate. In corrispondenza metto una tacca sul piano del cuneo e sulla base del cubo.

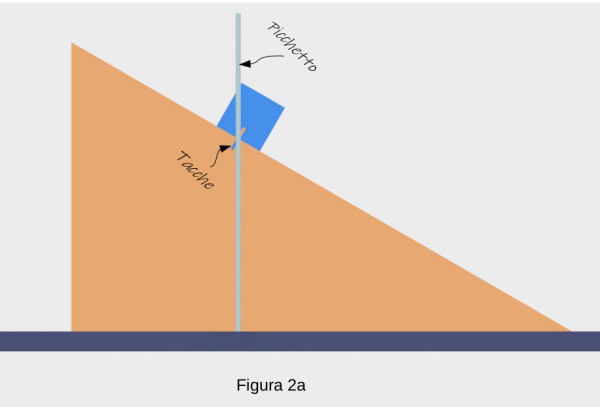
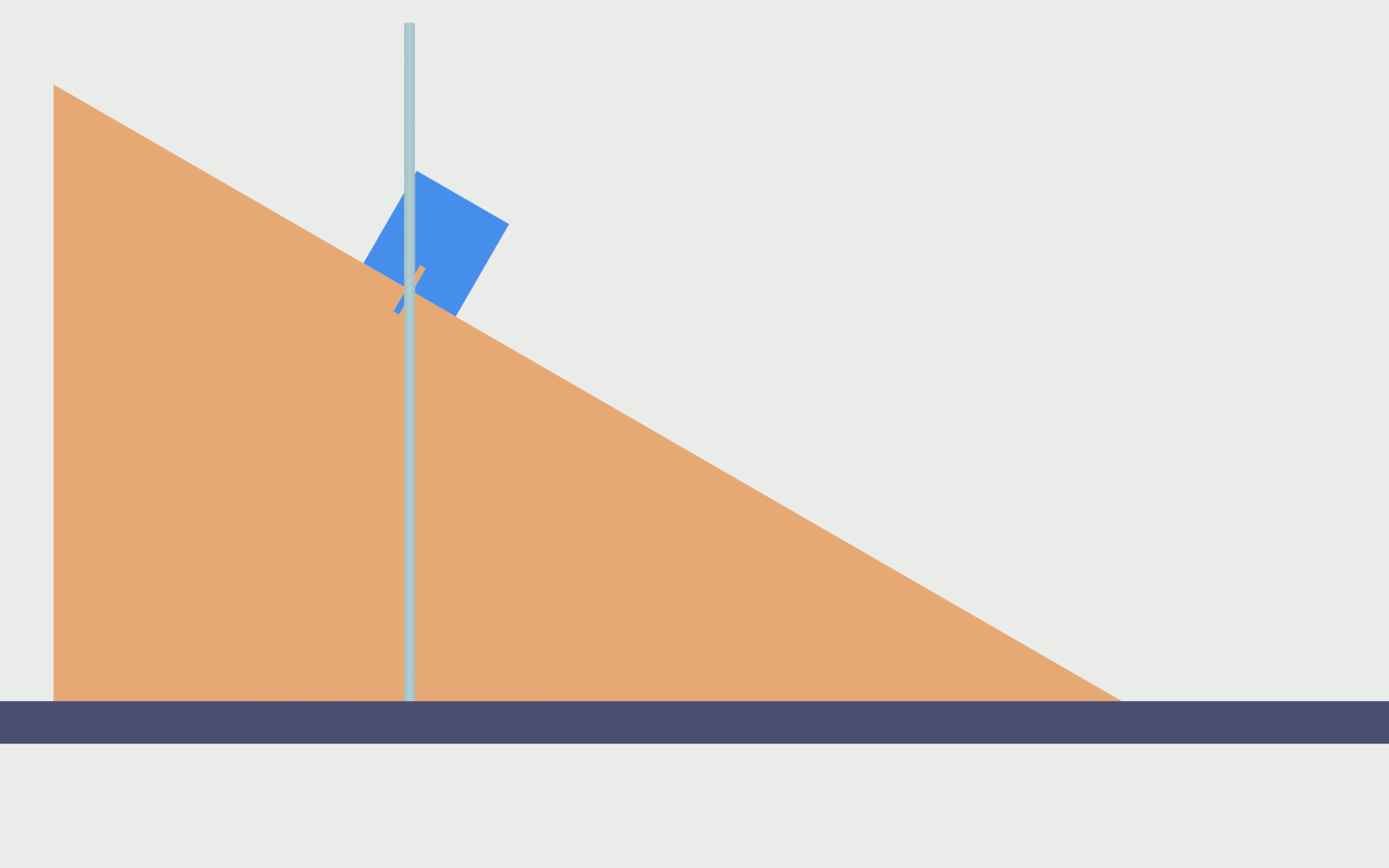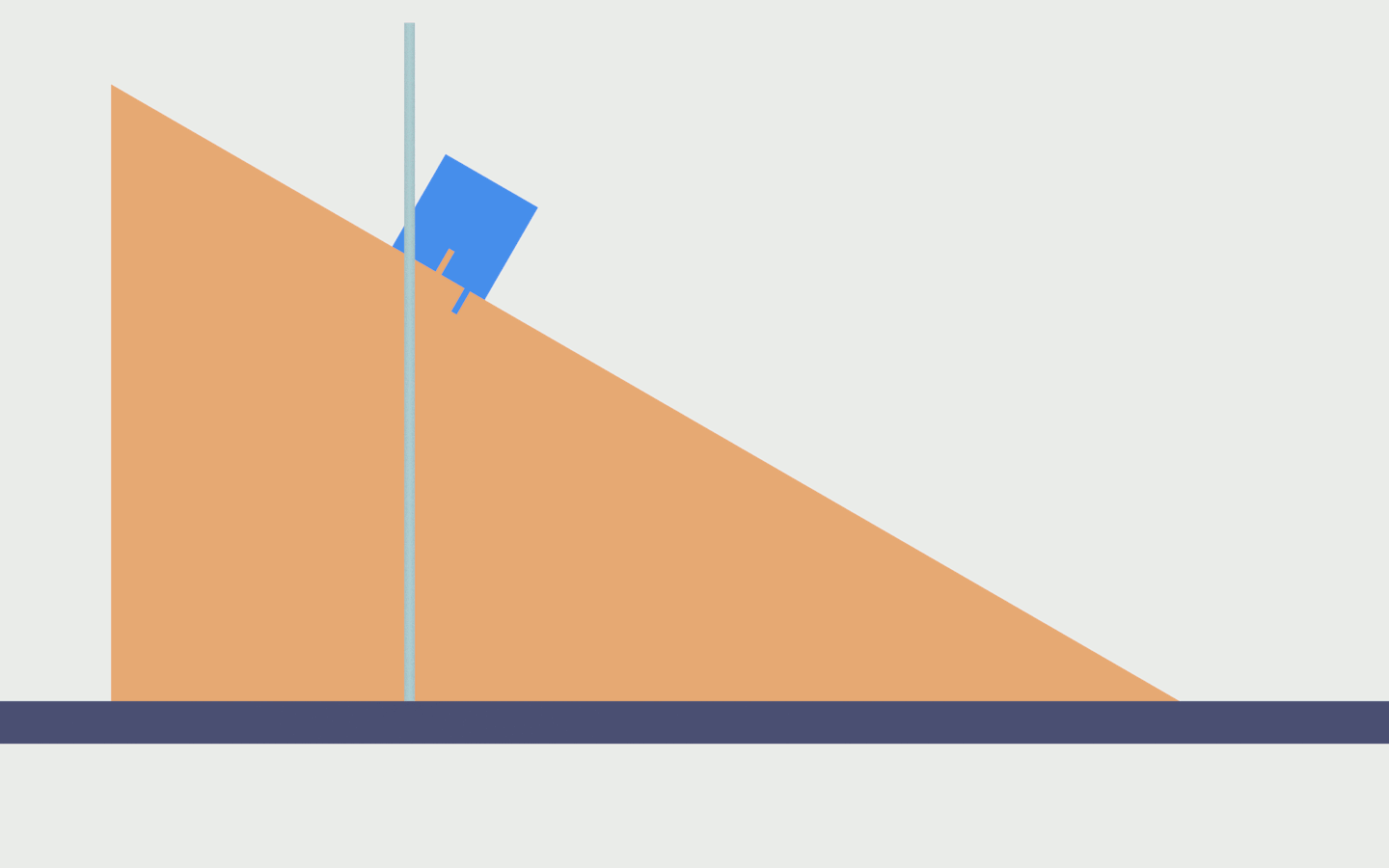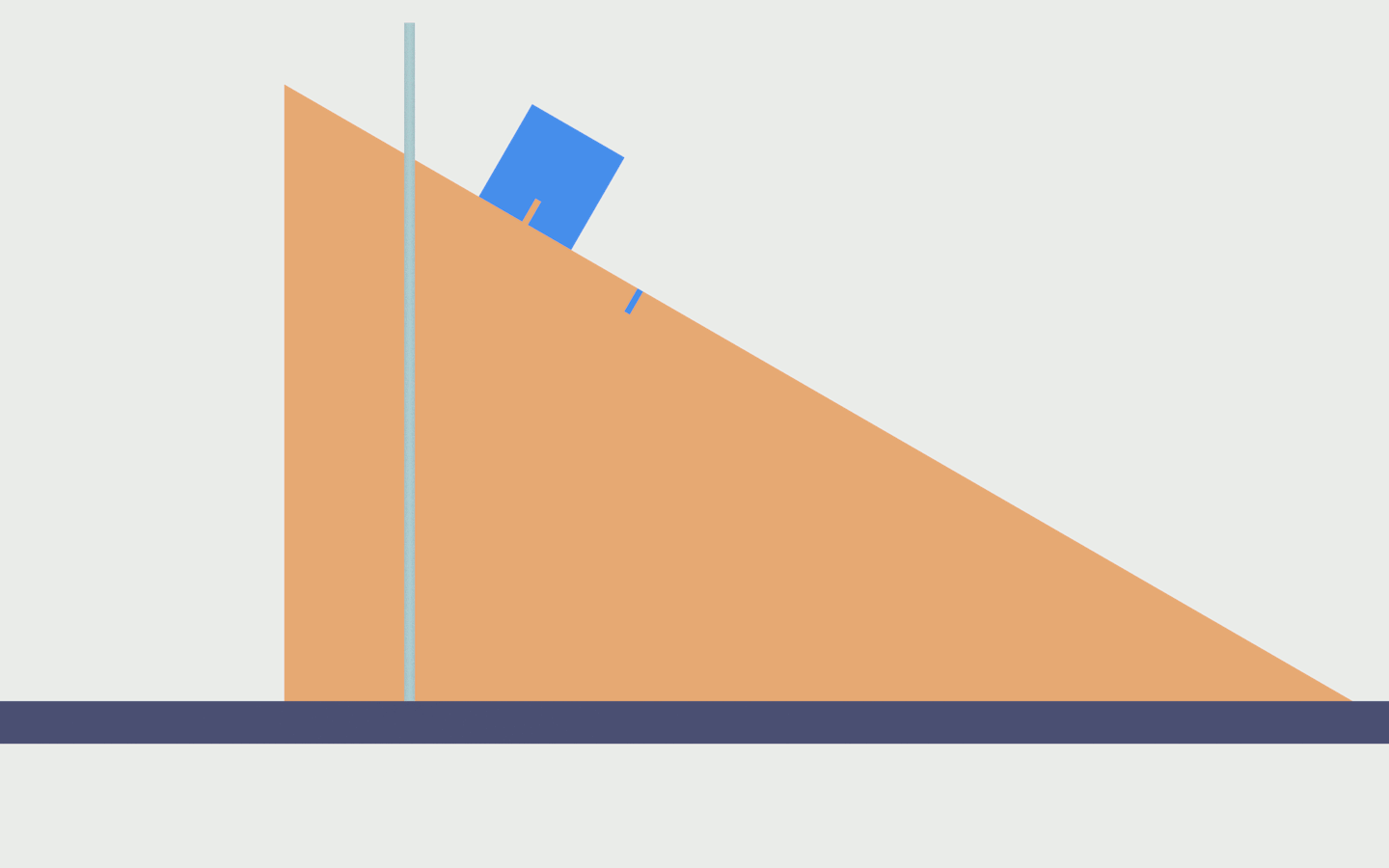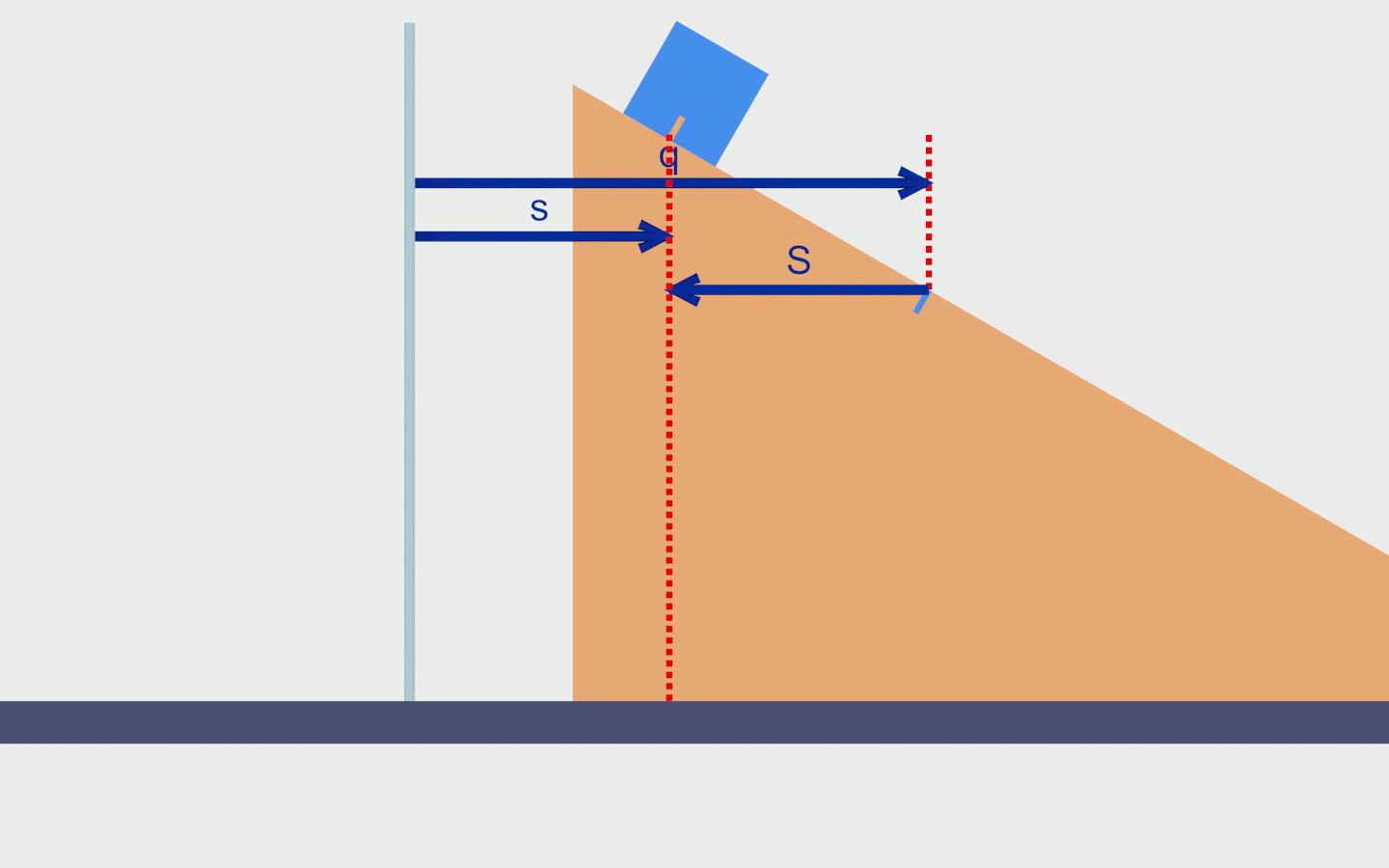
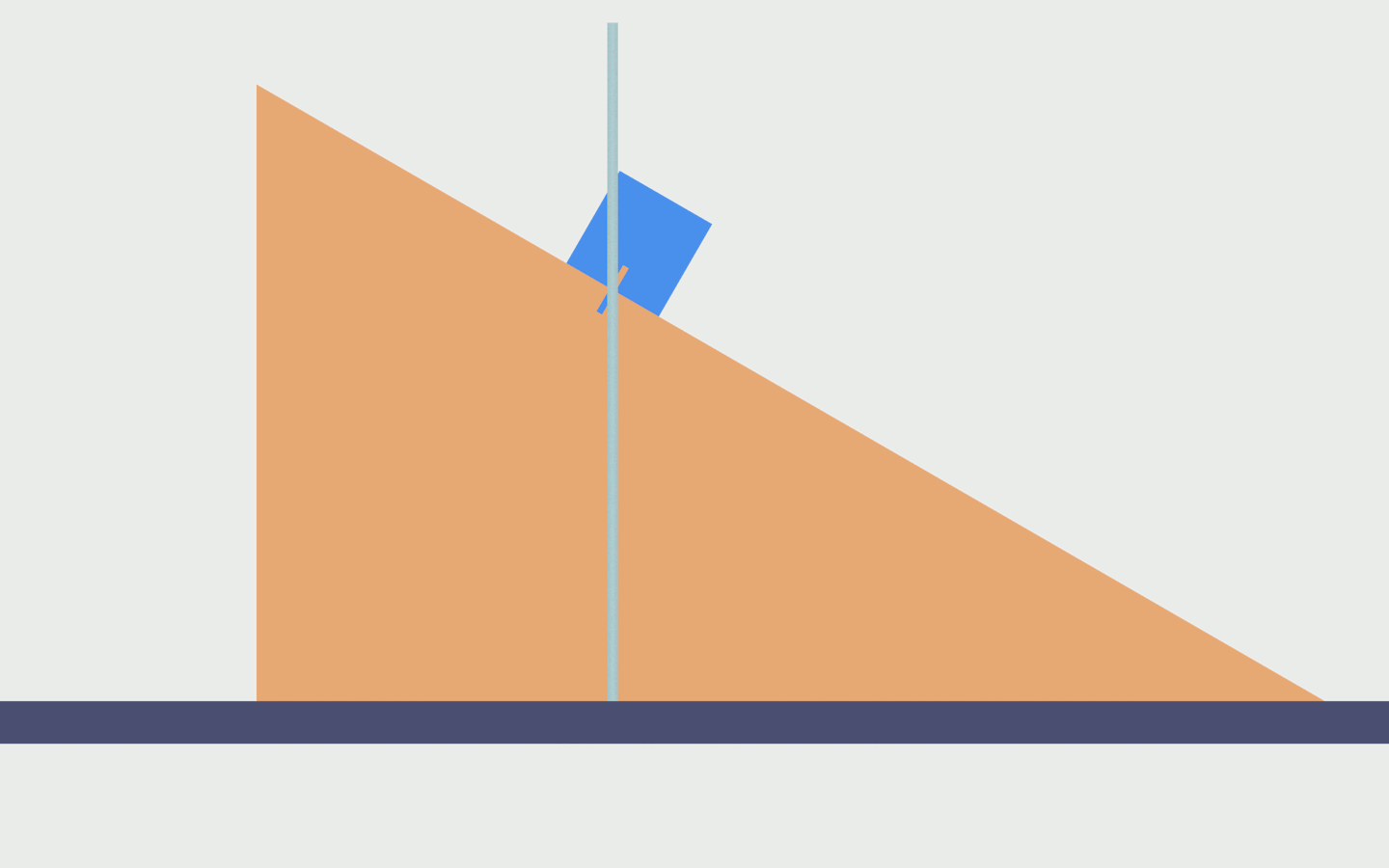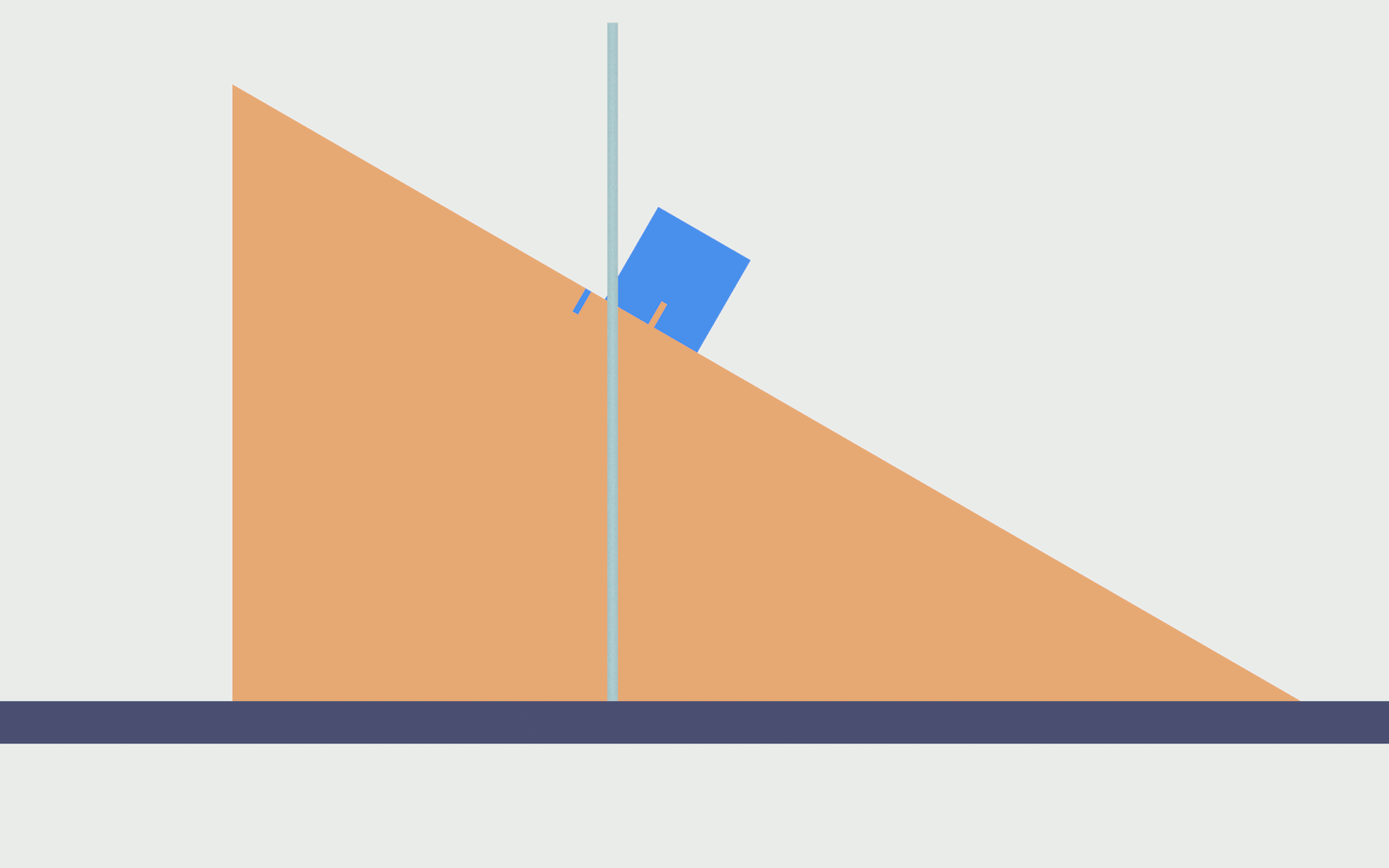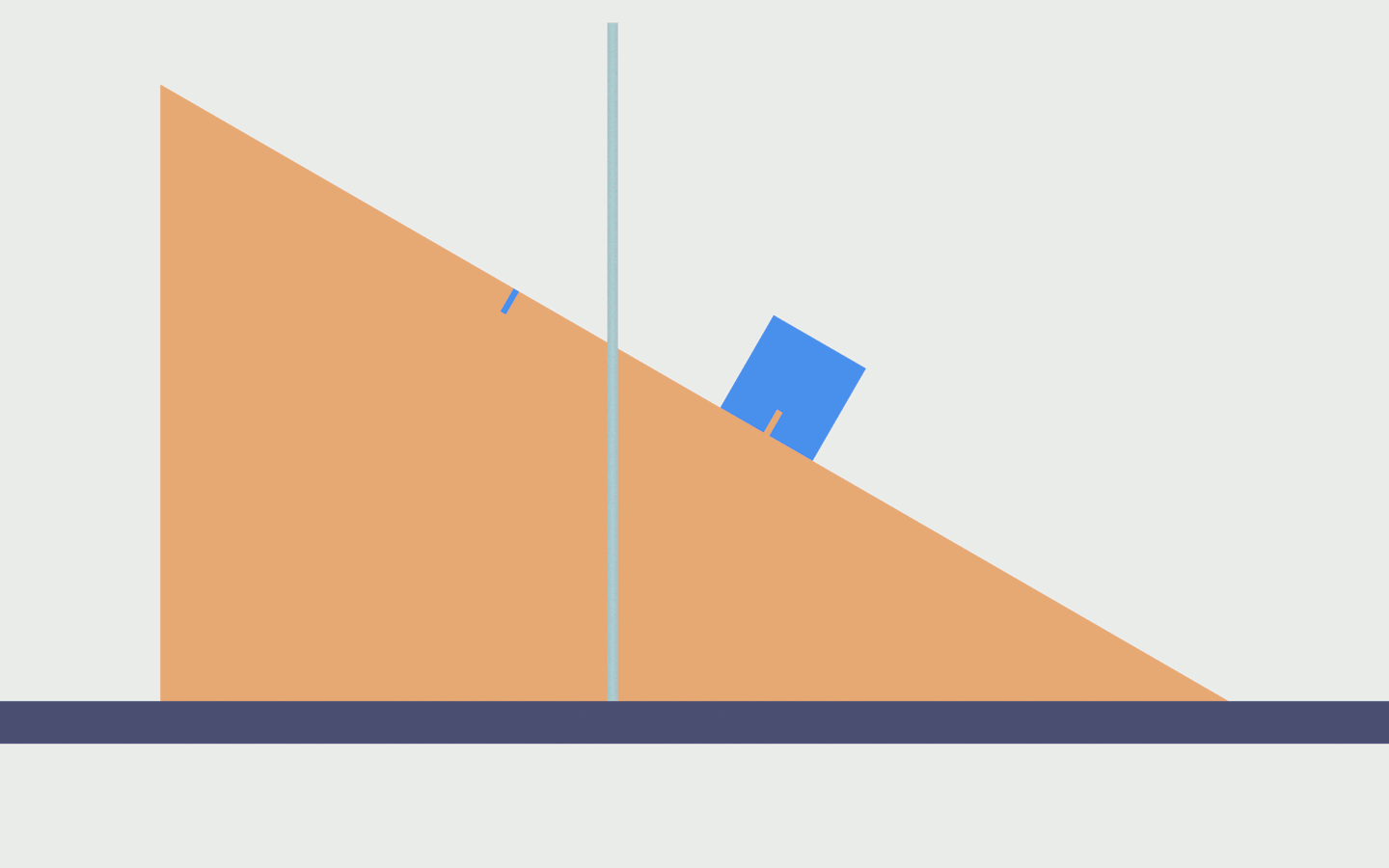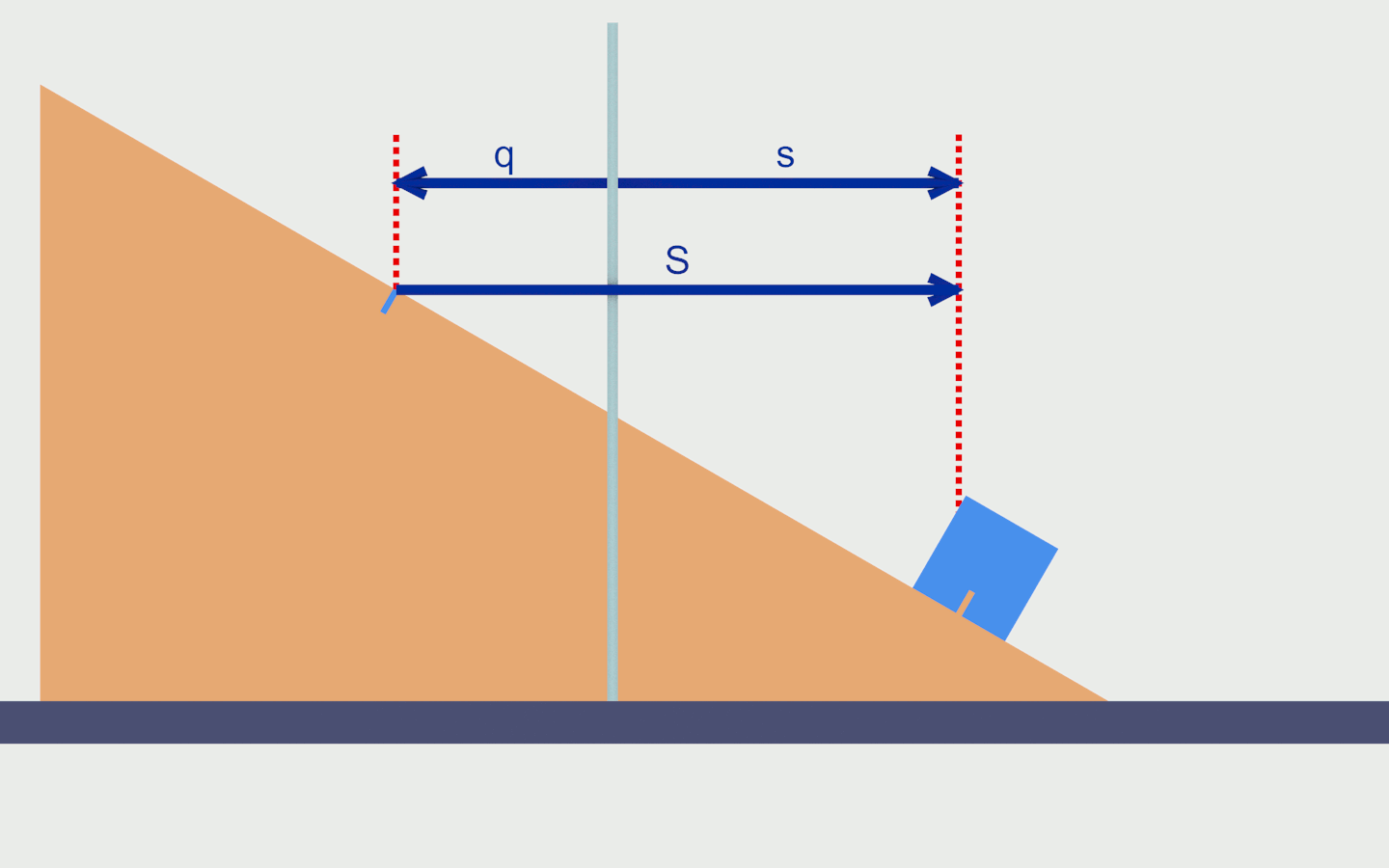
La distanza orizzontale tra il picchetto e la tacca sul cuneo sarà una delle nostre coordinate. Se trovo il cuneo a sinistra del picchetto considero il valore della coordinata positivo, se lo trovo a destra considero il valore della coordinata negativo. Conviene dare un nome specifico a ciascuna di queste coordinate, chiamo q quella che abbiamo appena definito.

 

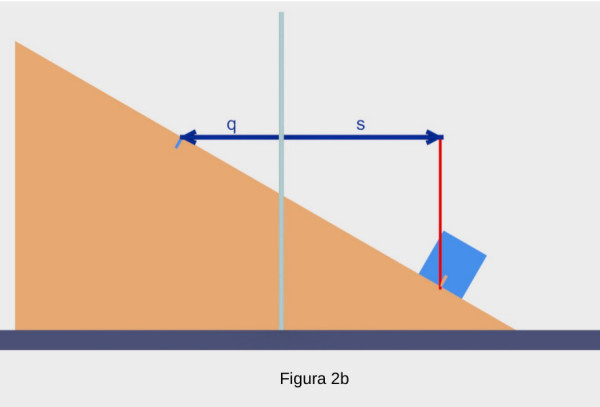
In modo simile, scelgo come altra coordinata la distanza orizzontale tra il picchetto e la tacca sul cubo. La considero positiva quando il cubo è a destra del picchetto. Chiamo s questa coordinata.

Credo non ci siano dubbi che questa coppia di coordinate (q,s) siano sufficienti per definire le posizioni orizzontali del cubo e del cuneo. Peraltro ci sono direttamente date nel sistema di riferimento solidale con la base.

Per esplorare le possibilità che ci dà Lagrange, proviamo a fare una scelta diversa per la seconda coordinata.

Invece di considerare come riferimento per la misura il picchetto, considero come punto di riferimento la tacca sul cuneo. In questo modo considererei come seconda coordinata la distanza orizzontale tra la tacca sul cuneo e la tacca sul cubo. Se il cuneo è a sinistra del cubo, considero la coordinata positiva. Chiamo S questa coordinata.

Ma questa scelta sarebbe legittima?

Certo che è legittima. Per Lagrange va ben quasi tutto, basta che mi ricordi di come l’ho definita quando andrò ad esprimere l’energia cinetica e l’energia potenziale. Una obiezione potrebbe essere che il riferimento sul quale baso la misura, la tacca sul cuneo, è in movimento e questo movimento risulterà anche accelerato. Va bene lo stesso, non modifica in nessun modo il metodo di Lagrange. Teniamoci quindi anche questa seconda coppia di coordinate (q,S) per esplorare questa alternativa. Notiamo anche che S=q+s (figura 3).

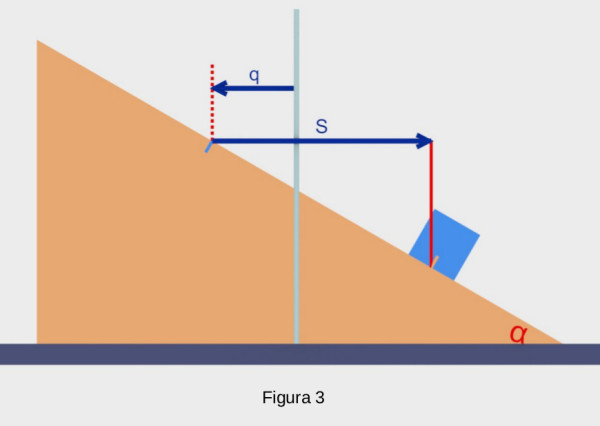
Passiamo al movimento verticale del cubo. La posizione verticale del cubo potrebbe essere definita da una coordinata z che misura di quanto si è spostato verticalmente il cubo, positiva verso l’alto. Notiamo però che la posizione verticale non è libera, il cubo deve essere appoggiato sul cuneo. Questo vincolo ci permette di trovare che z è completamente determinato dalle altre coordinate. Nella figura 4 si vede che la coordinata z è un cateto del triangolo rettangolo evidenziato.

S è l’altro cateto di questo triangolo e l’angolo opposto a z è ancora α. Per la definizione di tangente abbiamo che . Il segno meno indica che z è negativo quando S è positivo. Quindi non è necessaria una terza coordinata per determinare la posizione degli elementi del sistema. Tra l’altro si vede un piccolo vantaggio nell’utilizzare S, almeno per determinare z.

Ricordo che Lagrange ci impone di utilizzare il numero minimo indispensabile di coordinate necessario per definire la configurazione del sistema. In questo caso sono 2 (gradi di libertà del sistema). Possiamo scegliere le coppie (q,s) o (q,S) o una delle altre infinite alternative, ma devono essere sempre 2.

Mi sono dilungato molto su questa prima fase. Mi è sembrato utile rendere esplicite una serie di scelte che spesso sono fatte implicitamente nella impostazione della ricerca della soluzione.

Il metodo di Lagrange ammette una maggiore possibilità di scelta del metodo di Newton. Praticamente è in questa fase che chi cerca la soluzione può far valere le sue doti di fantasia.

Ma se al metodo di Lagrange può andare bene praticamente qualsiasi scelta, perché ragionarci tanto. Prendiamo la prima scelta che ci viene in mente!

È vero che qualsiasi scelta può andare bene, ma le espressioni che si ottengono per la Lagrangiana sono diverse. Alcune più trattabili di altre. Per questo, la scelta delle coordinate può essere importante per arrivare alla soluzione.

Qui finiscono le scelte da fare. Ora abbiamo gli elementi per sviluppare l’espressione della Lagrangiana con le coordinate che abbiamo scelto.

 

Prima di inoltrarci in questo percorso, anticipo qui i risultati che troveremo. Penso che sia più facile analizzarli a questo punto, in prossimità del testo che tratta delle coordinate, prima di affrontare la parte più matematica del metodo.

Nel caso vogliate continuare con il metodo di Lagrange e poi analizzare i risultati potete trovare la prosecuzione qui.

Il metodo di Lagrange ci porterà a trovare le leggi con le quali si sviluppano nel tempo le coordinate scelte. Nel nostro caso otterremo questo risultato attraverso l’espressione delle accelerazioni.

Scriviamo le accelerazioni con una notazione inventata da Newton. Questo tipo di notazione torna utile nel metodo di Lagrange perché semplifica la lettura delle espressioni che incontreremo.

In questa notazione le accelerazioni relative alle coordinate che abbiamo incontrato sopra sono indicate con: .

Le loro espressioni con gli sviluppi descritti più avanti sono queste:

Alcune osservazioni sui moti del cubo e del cuneo

Le tre accelerazioni sono costanti, data la configurazione del sistema che fissa F, M, m e α.

Nel nostro caso, questo significa che il segno delle accelerazioni fissa il verso del moto. Nota che le velocità iniziali sono nulle. Non ci può essere inversione del verso delle velocità.

Viste le definizioni delle coordinate, le relazioni tra verso dei moti e segno delle accelerazioni sono quelle in questa figura.

Se fossero tutte possibili avremmo 8 combinazioni. Quello che troveremo è che solo 3 di queste combinazioni sono possibili.

Disponendo delle espressione di queste accelerazioni, valutiamo se e quando questi spostamenti possono verificarsi.

Per primo osserviamo

Il denominatore è positivo e tutti gli addendi sono positivi, almeno per .  è sempre positivo.

Il cubo si muove sempre verso destra.

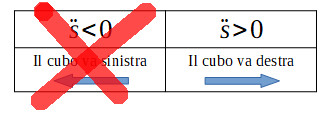
Così 4 combinazioni sono eliminate e ne rimangono ancora 4.

Ora vediamo 

Questa espressione può avere entrambe i segni. Proviamo a vedere quando prende l’uno o l’altro segno.

Il risultato è in questo grafico.

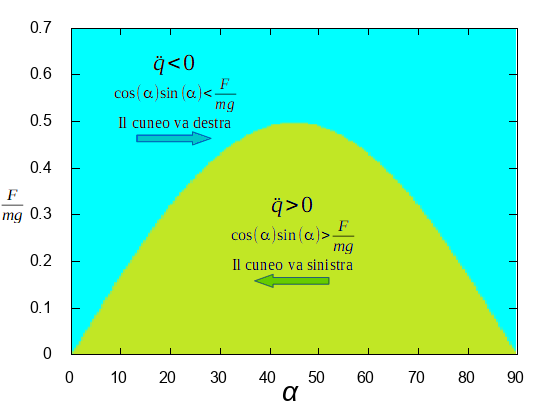
Vediamo i passaggi per ottenere il grafico.

Ricordiamo che moltiplicare o dividere per un numero positivo non cambia il segno dell’espressione. In questo modo possiamo ottenere delle espressioni semplificate che hanno lo stesso segno di . Questo ci permette di identificare gli elementi essenziali che condizionano il segno.

Per primo possiamo togliere di mezzo il denominatore che è sempre positivo.

Per leggere meglio questa espressione ricorro ad un paio di nozioni trigonometriche di base.

L’espressione di sopra diventa:

Alla fine otteniamo questa espressione ridotta che possiamo dire ha lo stesso segno di .

Questa espressione ci dice in quale verso orizzontale si muove il cubo.

La curva nel grafico è proprio . Se   allora è positivo ed il cuneo si muove verso sinistra (area verde). Altrimenti è negativo ed il cuneo si muove verso destra (area celeste).

Nel grafico ci sono due cose che mi hanno sorpreso.

La prima è che il verso del moto del cuneo non dipende dalla sua massa.

La seconda è l’effetto della inclinazione del cuneo. Immaginiamo una linea orizzontale in figura al livello di F/mg=0,4. Per angoli piccoli il cuneo va verso destra. Se l’inclinazione supera circa 26°, nelle stesse condizioni delle forze, il cuneo va verso sinistra. Per angoli ancora più grandi, superiori a circa 64° il cuneo riprenderebbe a andare verso destra.

Trattiamo ora

L’espressione trovata ci dice il verso del moto verticale del cubo come mostra questo grafico.

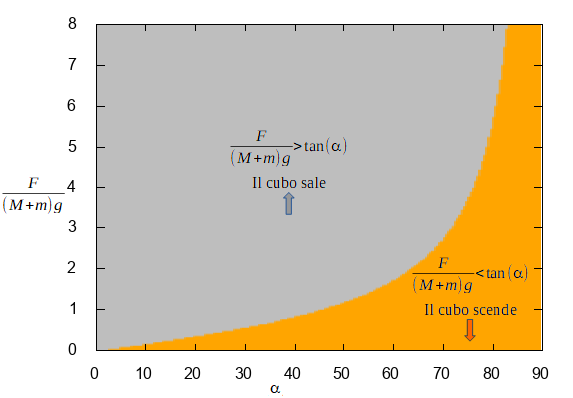
La curva nel grafico è . Se   allora  è positivo ed il cubo scende  (area arancio). Altrimenti  è negativo ed il cubo sale (area grigia).

Quindi ci sono configurazioni nelle quali il cubo sale ed altre nelle quali in cubo scende. Configurazioni nelle quali il cuneo va verso sinistra ed altre nelle quali va verso destra.

Ma tutte 4 le combinazioni sono possibili?

Partiamo delle due espressioni che abbiamo utilizzato.

Ci sono due legami tra i termini di queste due espressioni.

Il primo credo sia evidente. Il denominatore a destra è certamente più grande di quello a sinistra.

Per il secondo ci vuole un po’ di trigonometria per trovare che è equivalente a , che è sempre vera.

Vediamo il caso in cui , cioè il cuneo va verso sinistra,

Posso inserire i due legami con l’altra espressione visti sopra e troviamo che

Questo significa che, se il cuneo va verso sinistra necessariamente il cubo scende.

Alla fine rimangono solo 3 possibilità.

Il cuneo va verso sinistra. Il cubo scende andando verso destra.

Il cuneo va verso destra. Il cubo scende andando verso destra.

Il cuneo va verso destra. Il cubo sale andando verso destra.

Ora possiamo riprendere il discorso sul metodo di Lagrange per vedere come si ottengono le espressioni delle accelerazioni che abbiamo analizzato sopra.

Da qui in poi non abbiamo scelte da fare, il momento delle scelte ha riguardata riferimento e coordinate. Dobbiamo "semplicemente" seguire il metodo, direi quasi in modo automatico. Vedremo che le entità fisiche da considerare sono semplici da definire. Eventualmente la difficoltà può esserci in alcuni passaggi matematici. Questo è quello che voleva Lagrange. Già è significativo il titolo, "Mécanique analitique", che ha dato al suo libro del 1788. Poi ce lo ha detto esplicitamente nella introduzione al suo libro:< "..ridurre, sia la teoria di questa scienza sia l'arte di risolverne i problemi che presenta, a delle formule generali, il cui semplice sviluppo fornisca tutte le equazioni necessarie per la risoluzione del problema" e "I metodi che espongo non richiedono né costruzioni geometriche né ragionamenti geometrici o meccanici, ma soltanto operazioni algebriche" Con questo marca la differenza con i metodi "Newtoniani" fino ad allora utilizzati..  Lo sviluppo che segue può essere un esempio significativo di come il proposito di Lagrange si realizza: "...soltanto operazioni algebriche".

Dobbiamo trovare l’espressione della Lagrangiana del nostro sistema.

Lagrangiana= Energia cinetica – Energia Potenziale

Ricordo che Lagrange ci ha detto che questa espressione contiene tutti gli elementi per risolvere il problema.

Ripartiamo dall’energia cinetica.

L’energia cinetica del sistema è la somma delle energie cinetiche del cuneo e del cubo (espresse nel sistema di riferimento). Dobbiamo esprimerla con le coordinate che abbiamo scelto, (q,S).

Ricordiamo che l’energia cinetica, almeno nel caso in esame dove non ci sono rotazioni, è data da  della massa del corpo moltiplicata per la sua velocità al quadrato. Qui sono protagoniste le velocità.

Il cuneo si muove orizzontalmente: La sua posizione nel riferimento della base, quello che abbiamo scelto sopra, è data proprio dalla coordinata q. La velocità è data dal rapporto tra lo variazione della coordinata ed il tempo trascorso. Per tempi piccoli è la derivata della coordinata nel tempo, dq/dt. La scrivo in modo più compatto come , nella notazione inventata da Newton.

L’energia cinetica del cuneo è quindi

Il cubo si muove sia orizzontalmente sia verticalmente. Nel riferimento della base la sua posizione orizzontale è data dalla coordinata s, mentre quella verticale è data da .

La velocità orizzontale è quindi  e la velocità verticale è . Queste due velocità sono perpendicolari tra loro. Per ottenere in valore della velocità totale posso usare il teorema di Pitagora. . La lascio al quadrato perché è quello ci serve per ottenere l’energia cinetica.

L’energia cinetica del cubo è quindi .

L'espressione dell’energia cinetica totale , somma delle energie cinetiche del cuneo e del cubo, è quindi questa

Passiamo al secondo termine della Lagrangiana: l’energia potenziale

Sopra sono state protagoniste le velocità, qui sono protagoniste le forze.

Nel nostro sistema ci sono 3 tipi di forze (figura 1). La forza di gravità che agisce sul cubo (mg) e sul cuneo (Mg). Un forza esterna orizzontale e costante, F, che agisce direttamente solo sul cuneo. Le reazioni dei 2 vincoli.

Dico subito che Lagrange ci dice che le reazioni dei vincoli senza attrito devono essere ignorate nella sua Lagrangiana. Questo ci toglie da un bel problema perché le reazioni dei vincoli non sono note a priori.

Le altre forze, le forze attive, che abbiamo sono tutte costanti. In questi casi l’energia potenziale può essere scritta come la forza moltiplicata per lo spostamento del corpo considerato positivo nella direzione opposta alla forza.

Applicandolo al caso pratico si capisce meglio. Consideriamo l’energia potenziale dovuta alla forza F applicata al cuneo. La forza F è diretta verso destra. Lo spostamento del cuneo, la coordinata q, l’abbiamo considerata positiva verso sinistra, cioè in direzione opposta ad F. Quindi l’energia potenziale è semplicemente q F.

Corrisponde al lavoro che la forza potrebbe fare muovendosi da una posizione all’altra.

Ragionamento analogo per la forza di gravità sul cubo. La forza di gravità è diretta verso il basso. Dobbiamo considerare la componente degli spostamenti nella direzione della forza. Vale a dire gli spostamenti verticali del cubo, z. Se li consideriamo positivi verso l’alto, abbiamo visto sopra che . Quindi l’energia potenziale del cubo dovuta alla forza di gravità è .

Ci manca solo l’energia potenziale del cuneo dovuta alla gravità. Ma il cuneo si può muovere solo orizzontalmente. Lo spostamento verticale è nullo, di conseguenza possiamo considerare nullo il contributo della gravità alla sua energia potenziale.

Siamo arrivati ad avere tutti gli elementi per scrivere l’energia potenziale totale

La nostra Lagrangiana è: Se volessimo scriverla utilizzando la coppia di coordinate alternativa (q,S), dobbiamo sostituire s con (S-q) (figura 3).

Ho messo in evidenza in blu le variabili di queste espressioni. Ci tornerà utile più avanti.

Abbiamo così trovato la Lagrangiana del nostro sistema espressa con le due coppie di coordinate alternative.

Lagrange ci dice anche come utilizzare la Lagrangiana per ottenere le equazioni del moto dei due oggetti

Dobbiamo inserire la Lagrangiana in alcune equazioni, una per ciascuna coordinata. Nel nostro caso sono quindi 2. La forma delle equazioni è sempre la stessa. Utilizzando le coordinate (q,S), le equazioni appaiono così:

Notate che la forma dell’espressione è la stessa sia per coordinate inerziali (q) sia per coordinate non inerziali (S).

Queste espressione si chiamano equazioni di Eulero-Lagrange.

Apparentemente terribili! Se però andiamo a suddividere il problema vedremo che sono abbastanza trattabili.

Trattiamo separatamente ciascun termine e poi ricomponiamo il tutto.  Le affrontiamo nell’ordine della numerazioni indicata sopra.

Partiamo da quello che sembra più semplice, almeno come forma.

Ci chiede di fare la derivata parziale della Lagrangiana rispetto alla variabile q.

La derivata parziale è solo una derivata che tiene conto della variabile solo dove appare esplicitamente nella espressione. Il resto è da trattare come una costante. Niente di più.

Allora inserisco l’espressione della Lagrangiana e metto in evidenza in rosso dove appare la variabile . Notate che non è evidenziato. Devo considerare , la derivata rispetto al tempo di , una variabile diversa da .

♠ Tutti gli addendi che non contengono q sono da considerare costanti. La derivata di una costante è 0. Quindi la loro derivata parziale rispetto a q di questi termini è 0.

♦ La derivata di q rispetto a q è 1. Tanto cresce la variabile, tanto cresce la funzione. Il fattore costante F moltiplica anche la derivata.

Alla fine otteniamo che:

Qui potete trovare qualche informazione in più sulle derivate parziali.

Abbiamo completato il primo passo.

Passiamo all’altro addendo.

Per il momento consideriamo solo la derivata parziale

♠ Tutti gli addendi che non contengono  sono da considerare costanti. La loro derivata parziale rispetto a  è quindi 0.

♦ La derivata di una variabile elevata ad una potenza qualsiasi è . Qui n=2 ed abbiamo  al posto di x.

▲ Qui  non è direttamente elevato al quadrato, ma è elevata al quadrato una sua funzione (). In questi casi devo trattare questa funzione, cioè tutto quello che è tra le parentisi tonde, come una unica entità e fare la derivata rispetto a questa entità. Per il modello di derivata visto sopra  , dove x è (), ottengo . Devo moltiplicare questo risultato per la derivata rispetto a della funzione, . Questa derivata è uguale a -1, quindi modifica il segno del risultato trovato prima. In termini più matematici si tratta della derivata di una funzione di funzione che ha questo modello di sviluppo: , dove

Il risultato che ottengo è:

Inseriamo questa espressione nella equazione di Eulero-Lagrange

Arriviamo al terzo passo.

Dobbiamo fare la derivata totale rispetto al tempo di questa espressione.

La derivata totale ci chiede di tenere conto anche dei termini che possono variare nel tempo anche se non vediamo esplicitamente t nella loro espressione. Non dobbiamo considerarli costanti come per la derivata parziale. Questi si aggiungono ai termini dove appare esplicitamente t, ma qui non ci sono. Parlo del tempo perché è la variabile di derivazione.

Ho segnato in rosso questi termini. Devo quindi fare la loro derivata rispetto al tempo.

Fortunatamente questo caso è abbastanza semplice. Ci sono solo le due velocità, , e sono nella forma più semplice.

Con i due punti indichiamo la derivata della derivata, la derivata seconda, rispetto al tempo, cioè l’accelerazione.

Ora possiamo mettere insieme le parti della prima equazione di Eulero-Lagrange

Lo sviluppo della prima equazione di Eulero-Lagrange porta a questa espressione.

Passiamo alla seconda equazione. Le percorro un po’ più rapidamente tralasciando i commenti che sarebbero simili a quelli sopra.

Suddivido il problema in 3 parti.

Affronto la prima derivata parziale.

Questo è il risultato che ottengo.

Passo alla seconda derivata parziale.

 

Inserisco nella equazione di Eulero-Lagrange il risultato dello sviluppo della derivata parziale rispetto a .

Faccio la derivata totale rispetto a t del risultato ottenuto (passo 3).

Inserisco l’espressione ottenuto nella equazione di Eulero-Lagrange.

ed ottengo una seconda equazione

Quindi abbiamo ricavato due equazioni. L’evoluzione della posizione del cuneo e del cubo devono rispondere contemporaneamente ad entrambe le equazioni. Per questo diciamo che sono un sistema di equazioni.

In realtà sono un sistema di equazioni differenziali. Normalmente è la soluzione, analitica o numerica, di questo sistema che ci da' le leggi orarie del moto: . Notate che queste equazioni sono equivalenti a quelle ottenute con altri metodi. Le leggi orarire che otteniamo devono essere le stesse, indipendentemente dal metodo utilizzato per ottenerle.

In questo caso le equazioni sono molto semplici poiché contengono solo le accelerazioni e queste accelerazioni sono nella forma più semplice ( e non, ad esempio, )

Di fatto è un sistema di due equazioni lineari nelle due incognite  e .

Ci sono diverse possibilità per risolvere questo sistema. Qui ne uso una di applicabilità generale ha sistemi di questa forma.

La loro soluzione è data da queste espressioni:

Sostituendo i valori dei coefficienti del nostro caso diventano

Ed arriviamo finalmente al risultato.

Ricordiamo che q è la coordinata del cuneo nel riferimento fisso della base (distanza tra picchetto e tacca sul cuneo). S e la coordinata del cubo nel riferimento del cuneo (distanza tra le tacche).

La coordinata del cubo nel riferimento fisso che avevamo chiamo s è S-q. L’accelerazione del cubo sarà

Siamo arrivati alle tre espressioni delle accelerazioni che abbiamo analizzato sopra.

Per completare l'opera dovremmo trovare le leggi orarie dei moti del cubo e del cuneo.

Notiamo che  sono tutte accelerazioni costanti, questo semplifica il problema.

Quando l’accelerazione è costante ed il movimento inizia da fermo all’origine del riferimento vale la notissima formula per lo spostamento nel tempo che possiamo applicare al nostro caso

Così abbiamo ottenuto anche le leggi orarie.

 

QUI le altre soluzioni