Nessun problema per i nostri amici: basta applicare due volte la legge di gravitazione universale che conoscono molto bene…

Senza avvicinarsi troppo (la strumentazione è più che buona per misurare angoli piccoli), i nostri amici sistemano l’astronave in modo da semplificare la visione dell’orbita del satellite. In altre parole, la direzione pianeta-astronave è perpendicolare al piano orbitale del satellite, come mostrato nella Fig. 1. Tutto diventa piuttosto facile. In particolare, misurare l’angolo β sotteso dall’orbita (circolare) di raggio r del satellite (basta misurare l’angolo tra centro del pianeta e satellite) e l’angolo α sotteso dal pianeta di raggio R.

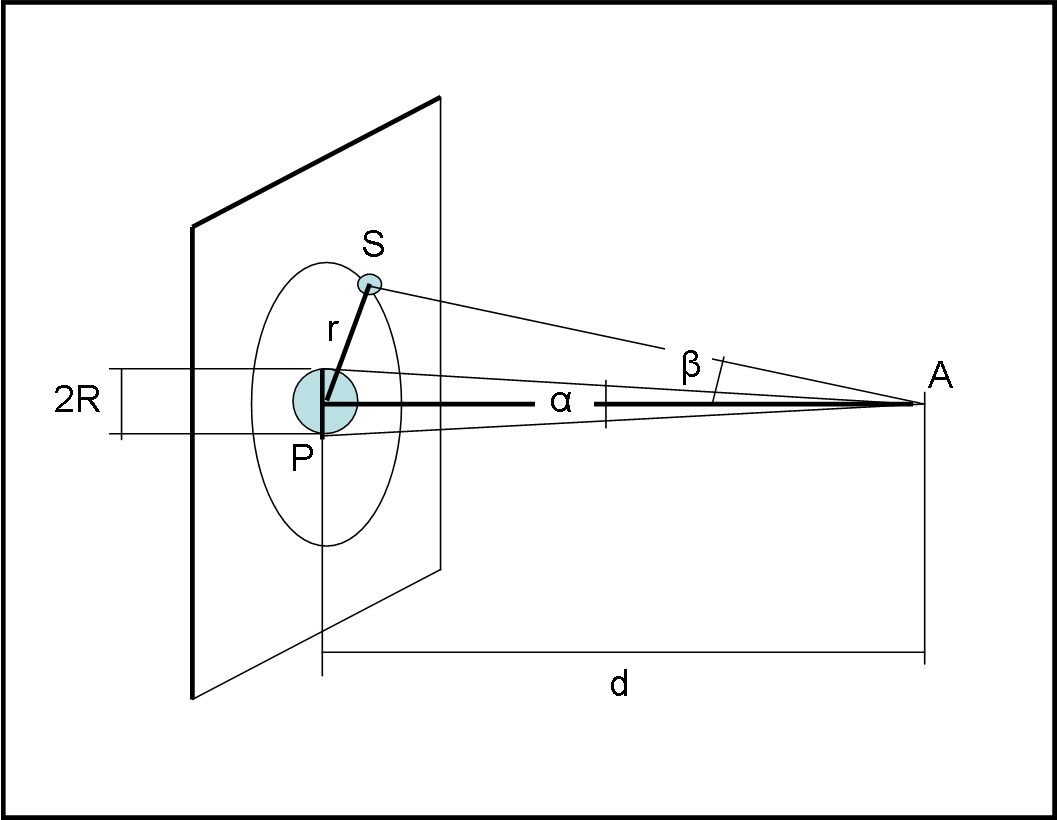
Conoscendo la distanza d (pianeta-astronave) è immediato calcolare il raggio r dell’orbita del satellite e il raggio R del pianeta

R = d tan (α/2)

r = d tan (β)

L’orbita del satellite è ben osservabile e non è difficile dedurre il periodo P in cui viene completata.

Se un satellite di massa m è in orbita attorno a un pianeta di massa M sappiamo benissimo quale legge deve seguire: quella di gravitazione universale. La forza a cui è soggetto il satellite è data da:

F = ma_S = GMm/r²

a_S = GM/r²

l’accelerazione a non è altro che l’accelerazione di gravità calcolata alla distanza r. Essa deve pareggiare l’accelerazione centrifuga, per cui:

GM/r² = ω²r       …. (1)

La velocità angolare ω è conosciuta, dato che è conosciuto il periodo P, e vale la ben nota relazione:

ω = 2π/P

Dalla (1) possiamo ricavare GM:

GM = ω²r³              …. (2)

Spostiamoci adesso sul suolo del pianeta. Anche chi si trova in quella posizione è soggetto alla gravità del pianeta: cambia solo la distanza dal centro, che adesso è R.

Risulta allora:

a_P = GM/R²

a_P = g è proprio l’accelerazione di gravità che vogliamo trovare. Scriviamo allora:

GM = gR²

Ricordando la (2) possiamo uguagliare le due espressioni e ottenere, infine:

g = ω²r³/R²

Chiedete ad Astericcio & co se il pianeta va bene per i loro muscoli e cose affini…

Il quiz è stato proposto QUI