QUIZ: prima di scendere è meglio conoscere il proprio peso **

04/08/16

QUIZ: prima di scendere è meglio conoscere il proprio peso **

Categorie: Sistemi extrasolari Tags: Scritto da: Vincenzo Zappalà Commenti:11
Un pianeta davvero interessante...
Un pianeta davvero interessante...

Un piccolo esercizio per i nostri piccoli amici Astericcio & co., sempre in giro per conoscere le meraviglie dell'Universo. Un problema, tuttavia, che viene normalmente affrontato anche nella realtà.

I nostri amici Astericcio & co. stanno navigando all’interno di un sistema planetario praticamente sconosciuto. Vedono diversi pianeti molto invitanti, ma, prima di scendere su di loro, vorrebbero sapere le condizioni che troverebbero una volta giunti al suolo. In particolare quanto vale l’accelerazione di gravità, da cui dipende il loro peso.

Fortunatamente, il più attraente, ha anche un satellite in orbita perfettamente circolare. L’unica cosa che conoscono i nostri amici è la distanza tra loro e il pianeta. Sono, comunque muniti di una strumentazione minima, tale da permettergli di misurare angoli anche molto piccoli.

Come devono sistemare la loro astronave (senza avvicinarsi troppo per non consumare carburante) e quali calcoli devono fare per trovare rapidamente l’accelerazione di gravità del pianeta ? Tralasciamo la figura, altrimenti il quiz diventa veramente ridicolo…

Soluzione QUI

Articoli correlati

11 commenti

  1. PapalScherzone
    04/08/2016 at 08:36

    Mumble... mumble...

    Se avessi saputo di dover risolvere questo quiz prima di atterrare nel tuo giardino, non lo so mica se avrei accettato il tuo invito... quasi quasi inverto la rotta e torno su Papalla finché sono in tempo!! :mrgreen:  :-P

  2. Vincenzo Zappalà
    04/08/2016 at 14:39

    caro Scherzy... non dire fesserie... lo risolverebbe anche Mimì... :mrgreen:

  3. Papalscherzone
    04/08/2016 at 15:28

    Bene! Allora glielo chiedo subito, così possiamo allacciarci le cinture di sicurezza e prepararci all'atterraggio!!

    :-D

  4. Vincenzo Zappalà
    04/08/2016 at 16:07

    Lei conosce sicuramente un certo simpaticone di nome Newton... :roll:

  5. Supermagoalex
    06/08/2016 at 01:22

    Dunque... per prima cosa dovremmo atterrare sul satellite.

    Noi sappiamo che g*=MG/(r+h)^2

    e al momento sono noti G e h.

    La massa M del pianeta la possiamo calcolare con la terza legge di Keplero (questo però dovrebbe essere possibile solo se la massa del satellite è molto inferiore a quella del pianeta), mentre conoscendo la velocità di rotazione posso calcolare il raggio del pianeta:

    v^2= GM/r

    A questo punto dovrei avere tutto per trovare g*

  6. Vincenzo Zappalà
    06/08/2016 at 05:06

    caro SMA...

    occhio che si dice: senza avvicinarsi troppo per non consumare carburante. Il che vuol dire stare a debita distanza sia dal pianeta che dal suo satellite... :roll:

  7. Supermagoalex
    06/08/2016 at 09:06

    Mi posso mettere in L1

  8. Vincenzo Zappalà
    06/08/2016 at 09:11

    Puoi metterti dove vuoi... basta vedere bene l'orbita del satellite... e poter misurare gli angoli...

  9. Arturo Lorenzo
    07/08/2016 at 00:29

    Sistemando l'astronave lungo sull'asse di rotazione del satellite intorno al pianeta, a distanza d dal centro di quest'ultimo, si osserverebbe il satellite ruotare attorno al pianeta descrivendo una circonferenza. Sperando che sull'astronave si disponga anche di un orologio, si misurerebbe quanto tempo impiega il satellite a compiere un giro completo (360 gradi = 2\pi radianti) attorno al pianeta. 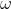A questo punto sarebbe nota la velocità angolare \omega con cui il satellite ruota attorno al pianeta. Ora, poiché nel moto circolare del satellite attorno al pianeta la forza centripeta eguaglia la forza gravitazionale, si ha:

    m\omega ^{2}r = G\frac{mM}{r^{2}}

    da cui, semplificando m (massa del satellite) :

    \omega ^{2}r = G\frac{M}{r^{2}}

    la quantità al secondo membro non è altro che l'accelerazione di gravità g, quindi:

    g = \omega ^{2}r                   (1)

    \omega la sappiamo per quanto detto sopra. Per calcolarci r , utilizziamo il fatto di conoscere la distanza d dal centro del pianeta e e di potere misurare gli angoli. In particolare, misuriamo l'angolo \theta compreso tra l'asse di rotazione del satellite attorno al pianeta e la congiungente l'astronave con il satellite. Consideriamo poi il triangolo avente come vertici l'astronave A, il centro del pianeta P e il centro del satellite S. Tale triangolo è rettangolo in P, perché l'orbita circolare del satellite giace su un piano perpendicolare all'asse di rotazione. Quindi posso applicare i teoremi dei triangoli rettangoli. In particolare mi calcolo r, cioè la distanza tra centro del pianeta e centro del satellite, con la :

    r = d *tg\theta

    A questo punto non mi manca nulla per calcolare la g tramite la  (1).

     

  10. Gianni Mastropaolo
    10/08/2016 at 13:20

    uhm ... condivido in parte, così si è calcolato g alla distanza r dal centro del pianeta, cioè  sull'orbita del pianeta. Penso che agli astronauti interessi g sulla superficie del pianeta nel caso volessero atterrare (appianetare?).

    Si sa che g è inversamente proporzionale al quadrato della distanza dal centro del pianeta.

    Credo che basti fare la proporzione conoscendo il raggio del pianeta, cosa possibile con la stessa triangolazione usata per il raggio dell'orbita  visto che lo strumento per misurare gli angoli ha una risoluzione elevata.

     

  11. Arturo Lorenzo
    10/08/2016 at 22:08

    Si, nel commento precedente ho utilizzato l'eguaglianza tra forza centripeta e forza di attrazione gravitazionale per trovare la g (che in effetti sarebbe quella in corrispondenza dell'orbita del satellite e non sulla superficie del pianeta). In realtà, tramite la stessa eguaglianza, mi ricavo piuttosto M, ossia la massa del pianeta:

    M=\frac{\omega ^{2}r^{3}}{G}        (quantità tutte note)

    A questo punto, per conoscere l'accelerazione di gravità che avvertirebbe l'astronave atterrando ad uno dei poli del pianeta, riapplico la legge di gravitazione universale, considerando che in questo caso la distanza dell'astronave dal centro del pianeta sarebbe R (con R raggio del pianeta):

    F=G\frac{m_{a}M}{R^{2}}=m_{a}\frac{w^{2}r^{3}}{R^{2}}

    da cui (P=m*g)

    g_{p}=\frac{\omega ^{2}r^{3}}{R^{2}}

    R lo si determinerebbe come hai descritto, con lo stesso metodo di triangolazione usato per determinare r.

    A questo punto, però, attendo la soluzione da parte del Prof  :wink:

     

     

     

     

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.