Questa soluzione in realtà nasce un po' come un gioco di squadra, stimolato da un quiz (qui) che come per magia si è trasformato in un mosaico, costruito tessera dopo tessera da diversi protagonisti: Valentina, Leandro, Paolo Salvini, Arturo ed il sottoscritto.

Ogni tessera ha la sua importanza per comporre il mosaico, come emerge chiaramente leggendo i commenti dei diversi giocatori...

Un gioco che non richiede complicate attrezzature, ma solo sei puntine da disegno...

La soluzione proposta utilizzerà uno dei possibili approcci per trovare la configurazione, o le configurazioni, che consentono ad ogni puntina di trovarsi alla medesima distanza da almeno altre tre puntine.

Il metodo proposto si basa su una caratteristica di una nota figura geometrica: tutti i punti che compongono la circonferenza di un cerchio hanno la medesima distanza dal centro del cerchio (raggio).

Per sfruttare questa caratteristica basta porre la puntina al centro del cerchio,  fissare un raggio qualunque e costruire la circonferenza del cerchio (lo stesso identico lavoro che svolge egregiamente un normale compasso).

Tutti i punti che hanno la stessa distanza (raggio) dalla puntina (centro del cerchio) giacciono necessariamente sulla stessa circonferenza.

Quindi per soddisfare la condizione posta dal quiz, sulla circonferenza di ogni puntina devono trovarsi almeno altre tre puntine.

E' del tutto evidente che le puntine, come dice Leandro, dovranno necessariamente fare amicizia tra loro.

Meglio, fare un passo per volta... provando a far sbocciare l'amicizia tra due puntine.

Per facilità posizioniamo le due puntine (azzurra e arancione)  su una linea orizzontale ad una certa distanza una dall'altra.

Se si vuole che la puntina azzurra si trovi sulla circonferenza arancione e che contemporaneamente la puntina arancione si trovi sulla circonferenza azzurra, come mostra la figura 2, basta usare la distanza tra le puntine come raggio “comune” su cui costruire due uguali circonferenze, una intorno alla puntina azzurra e una intorno a quella arancione.

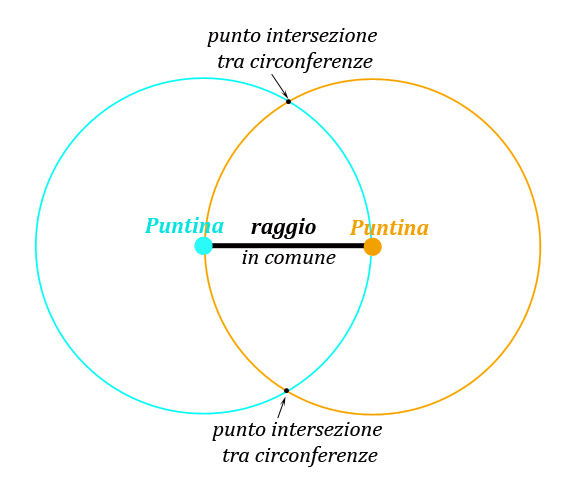
Sembra proprio che le due puntine abbiano fatto amicizia... e ci sono anche due interessanti punti dove le due circonferenze si intersecano...

Una terza puntina posizionata in uno di quei due punti, equidistanti da entrambe le puntine, sicuramente incrementerebbe il gruppo di amici...

Per facilità usiamo il punto inferiore per posizionare la terza puntina rossa.

Come mostra la figura 3, ora sulla circonferenza di ogni puntina giacciono  due puntine.

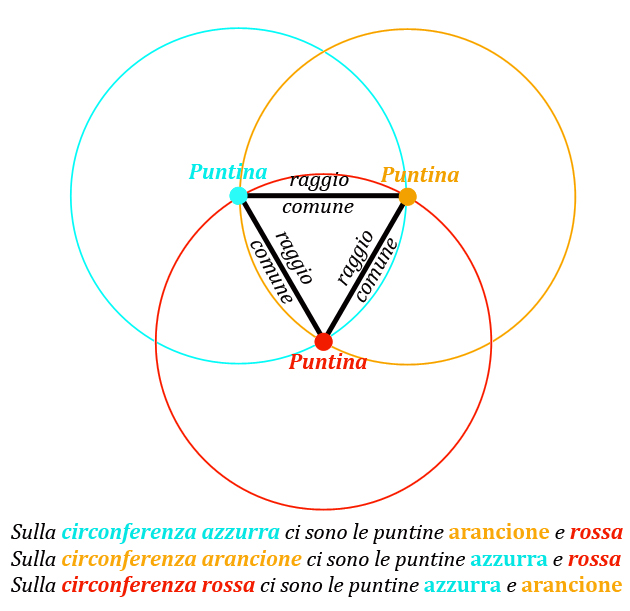
I tre raggi comuni che saldano l'amicizia tra le tre puntine formano proprio un bel triangolo equilatero!

Ricapitolando, l'amicizia tra tre puntine consente ad ogni puntina di averne due sulla sua circonferenza e di costruire una figura in cui le puntine rappresentano i vertici di un triangolo equilatero.

Un triangolo equilatero su cui ha insistito molto anche Paolo Salvini.

Viste le formidabili amichevoli proprietà del triangolo equilatero, che garantisce ad ogni puntina due puntine equidistanti (che giacciono sulla sua circonferenza), perché non sfruttarle con le tre puntine rimanenti?

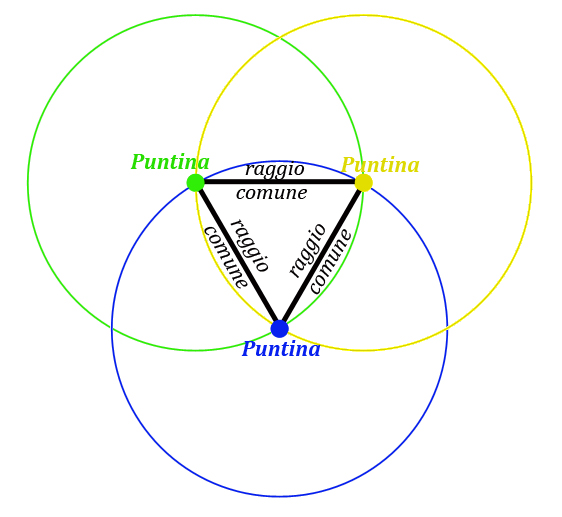
Questo secondo triangolo equilatero è identico al primo (il raggio è  lo stesso, ossia è di eguale lunghezza) ed ha lo stesso problema del primo, ossia ad ogni puntina ne manca ancora una per soddisfare la condizione di avere almeno tre puntine equidistanti (sulla sua circonferenza).

Come si può far fare amicizia a questi due triangoli?

Per stimolare l'amicizia tra i due triangoli equilateri, si potrebbero far cadere i vertici di questo secondo triangolo: uno sulla circonferenza azzurra, uno su quella arancione e l'ultimo su quella rossa.

Così facendo tutte le puntine avrebbero tre puntine alla stessa distanza, giacenti sulle loro circonferenze...

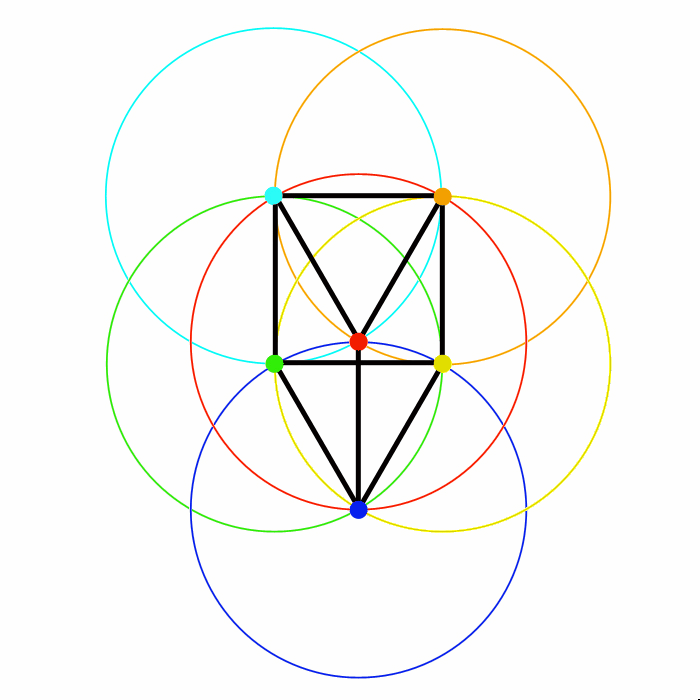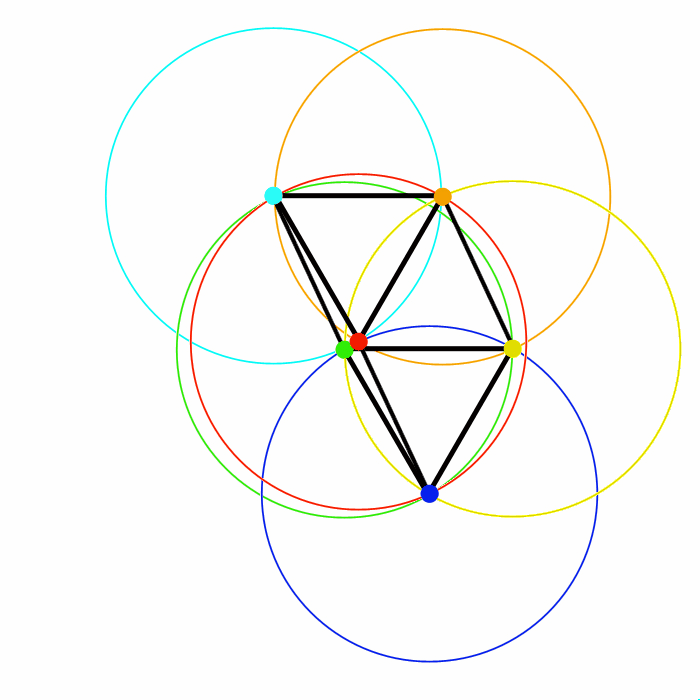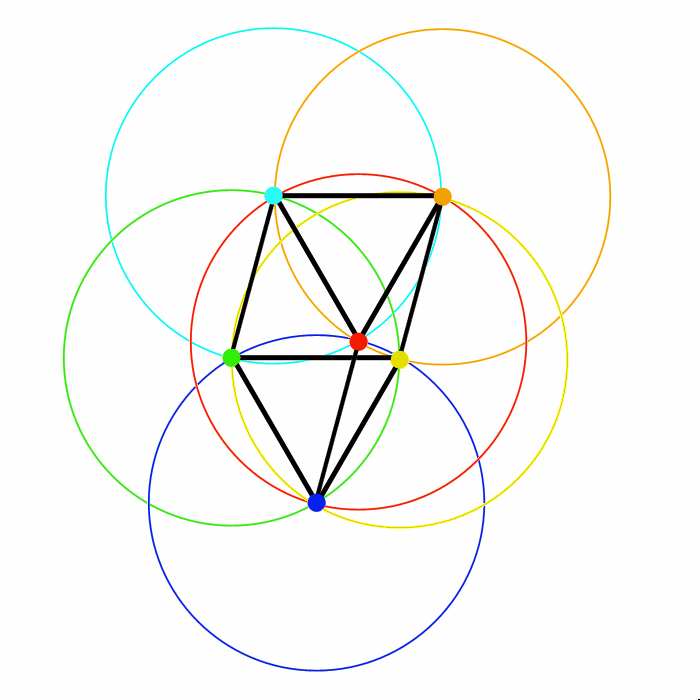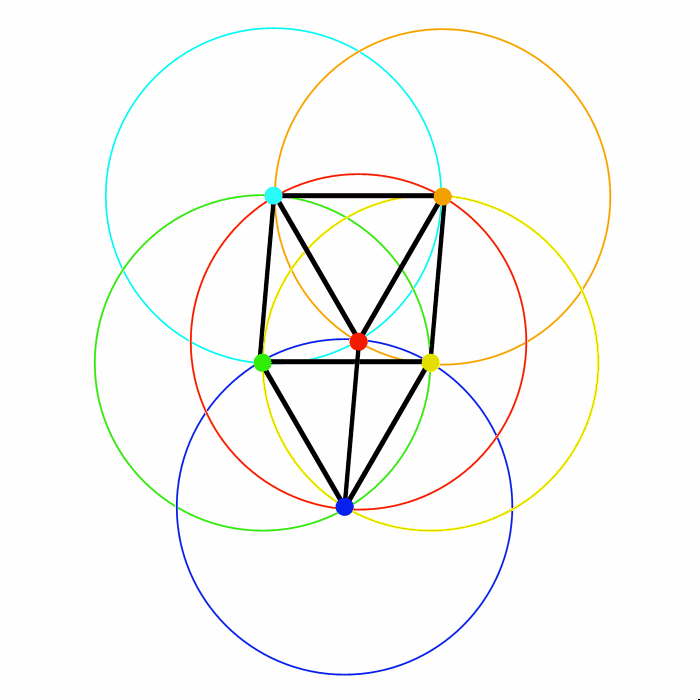
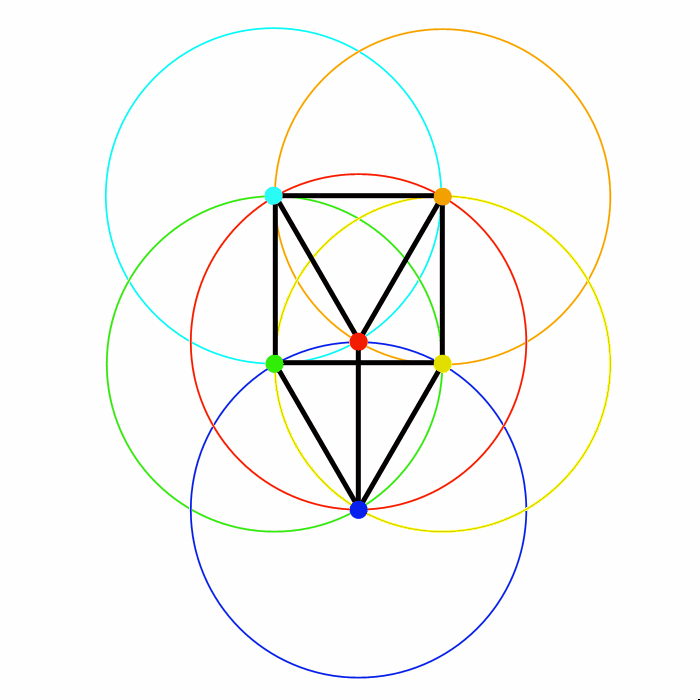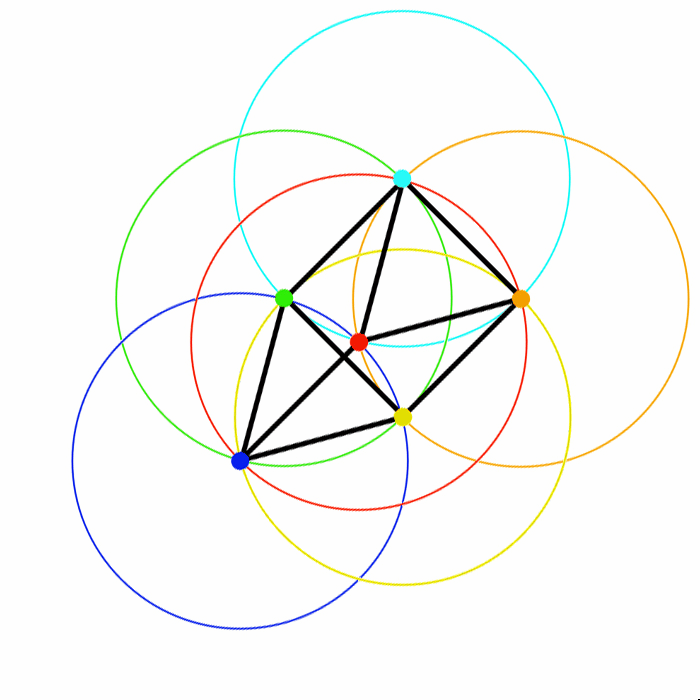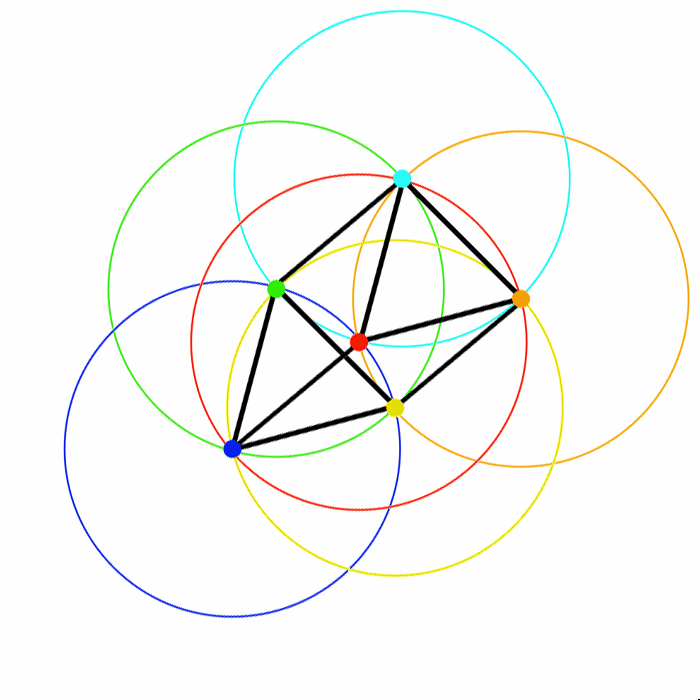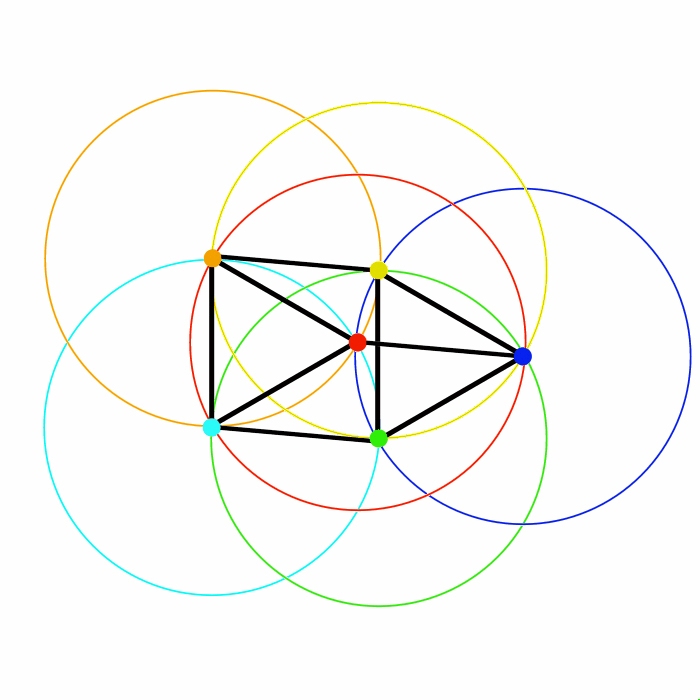
La Figura 5 sottostante mostra una delle possibili configurazioni che soddisfa le condizioni poste dal quiz. Soluzione che per prima è stata trovata dalla bravissima Valentina.

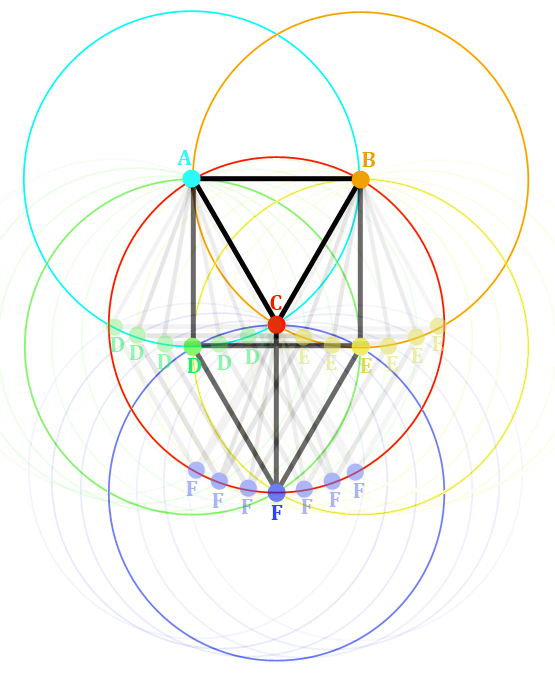
In fin dei conti è bastato posizionare il secondo triangolo equilatero sotto il primo, alla giusta distanza (raggio rosso), per far coincidere i vertici del secondo triangolo con le circonferenze del primo.

Ora ogni puntina ha tre puntine equidistanti (identico raggio in comune):

Le puntine B, C e D sono equidistanti da A;

Le puntine A, C e E sono equidistanti da B;

Le puntine A, B e F sono equidistanti da C;

Le puntine A, E e F sono equidistanti da D;

Le puntine B, D e F sono equidistanti da E;

Le puntine C, D e E sono equidistanti da F.

Sicuramente questa configurazione soddisfa le condizioni poste dal quiz, ma è l'unica possibile?

Decisamente, no, come dimostra il video “pendolare” di Arturo.

Inclinando dello stesso angolo i segmenti: A-D; B-E e C-F, i vertici del secondo triangolo (D, E e F) “risalgono” nel medesimo modo e della medesima quantità le circonferenze azzurra, arancione e rossa.

Nella figura 6 sottostante il vertice D (puntina verde) si muove lungo la circonferenza azzurra, il vertice E (puntina gialla) lungo la circonferenza arancione e quello F (puntina Blu) lungo la circonferenza rossa.

L'animazione mostra ancora meglio come tutte le configurazioni di questo strano pendolo soddisfino le condizioni poste dal quiz.

L'oscillazione raggiunge il suo massimo a destra quando il segmento A-D (azzurro-verde) raggiunge la stessa inclinazione del segmento A-C (azzurro-rosso), poiché la puntina verde si deve sovrapporre a quella rossa ed a sinistra quando il segmento B-E (arancione - giallo)  raggiunge la stessa inclinazione del segmento A-C (arancione - rosso), poiché la puntina gialla si deve sovrapporre a quella rossa.

Come mostra l'ultima figura 7, considerato che gli angoli di un triangolo equilatero sono uguali come i suoi lati, ogni suo angolo misura 60° (180°/3 = 60°),  l'oscillazione massima è pari a 30° a destra e 30° a sinistra per un totale di 60° di oscillazione.

Infine la stessa configurazione può anche essere orientata in modo differente.

All'inizio le prime due puntine erano state poste su una linea orizzontale, ma si potevano porre con un'inclinazione qualunque.

Benché la configurazione e il “movimento” a pendolo siano sempre gli stessi, come faceva notare anche Paolo Salvini i triangoli equilateri possono anche avere diversi orientamenti.

L'ultima animazione mostra proprio la configurazione precedente, con tre diversi orientamenti.... un po' come girare intorno alla figura 5 e vederla da diverse angolazioni, o se preferite come ruotare la tavola su cui abbiamo piantato le puntine da disegno.

Certo che sei piccole ed economiche puntine da disegno sono state capaci di stupirci con qualche amichevole gioco di prestigio, trasformandosi in uno stupendo pendolo...

Paolo