Categorie: Meccanica Celeste
Tags: energia meccanica leggi di Keplero momento angolare orbita Papalterra quiz soluzione velocità
Scritto da: Vincenzo Zappalà
Commenti:17
Soluzione (provvisoria) del quiz su Papalterra ***
La soluzione del QUIZ che riportiamo è quella dedotta da un’analisi fisica del problema, soggetta a certi vincoli geometrici. La riportiamo, tenendo presente che nei commenti è stata sollevata una soluzione apparentemente migliore, ancora tutta da investigare riguardo alla sua validità fisica. Ricordiamoci che vogliamo inserire un satellite in orbita e quindi impartirgli una certa velocità in un punto ben determinato.
Il problema è presto definito in Fig. 1.
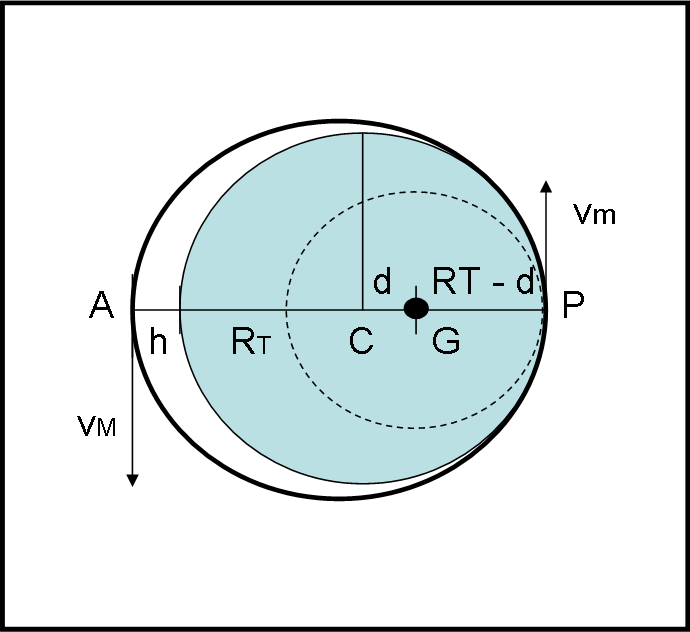
Abbiamo una Terra azzurra (Papalterra) con il baricentro G spostato di 100 km verso destra rispetto al centro della sfera C, e vogliamo trovare il minimo periodo di un satellite artificiale che possa orbitare attorno a lei. In particolare lo vogliamo confrontare con quello di un satellite che ruoti attorno alla Terra vera (baricentro = centro). In entrambi i casi permettiamo al satellite di muoversi ad altezza zero rispetto alla superficie (niente attriti e nessuna montagna o cose del genere, ossia una Terra e una Papalterra completamente lisce).
L'orbita circolare di un satellite che rivolva ad altezza zero è la stessa circonferenza terrestre. Il semiasse dell'orbita è, quindi, il raggio RT della Terra e Papalterra . Si trova di tutto e di più nella “rete”, ma a noi interessa poco il valore vero del raggio terrestre; a noi interessa fare un confronto tra una Terra e una Papalterra costruite "ad hoc", anche se estremamente simili al nostro pianeta, almeno da un punto di vista geometrico. Scegliamo perciò:
RT = 6371 km
La parte che segue (in corsivo) calcola il periodo del satellite PST, ma è del tutto inutile per lo scopo del problema. Vale, comunque, la pena riportarla come piccolo esercizio
Il periodo di rotazione PST si determina facilmente in funzione dell’accelerazione di gravità al suolo, un altro valore scelto in qualche modo, ma che deve rimanere sempre lo stesso, ossia:
g = 9.807 m/sec2
Si ha (il moto è circolare uniforme):
F = ma = GMm/RT2 = gm = m v2/RT
(g RT)1/2 = v = 2πRT/PST
PST = 2π (RT/g)1/2 = 2π (6371000/9.807)1/2 = 5064.26 sec
Questo è il periodo di riferimento rispetto al quale calcolare il rapporto finale tra i periodi.
Tuttavia, a noi, poco interessa, dato che basta ottenere un rapporto di periodi e la terza legge di Keplero ci evita il loro calcolo…
Dobbiamo adesso calcolare il MINIMO periodo del satellite in orbita attorno alla Terra con il baricentro spostato, ossia la Papalterra. Ma, come già detto prima, invece di calcolare il periodo è più che sufficiente determinare il semiasse dell’orbita
Scegliamo il perigeo in modo che coincida esattamente con il punto P della superficie della Papalterra, il più vicino al baricentro G (spostato di 100 km verso destra rispetto al centro della sfera C). Essendo il più vicino deve anche avere la velocità minima.
L’accelerazione, in quel punto, dovuta alla gravità (riferita al baricentro), è data da:
a = GM/(RT – d)2
Tuttavia, la velocità che bisogna impartire al satellite in quel punto deve essere tale che il raggio di curvatura dell’orbita non sia minore di RT, altrimenti il satellite penetrerebbe all’interno della Terra. La velocità deve perciò avere un valore minimo vm che dipenda dal raggio della sfera RT. In altre parole, la velocità vm deve essere quella di un moto circolare uniforme attorno alla Terra, la minima che non permetta uno scontro col suolo.
Dobbiamo allora scrivere:
GM/(RT – d)2 = vm2/RT
Dalla relazione precedente si ricava la velocità minima permessa:
vm = (GMRT)1/2/(RT – d) …. (1)
Non ci resta, adesso, che calcolare l’orbita corrispondente e, in particolare, determinare l’apogeo e la sua velocità.
Chiamiamo h la distanza dell’apogeo rispetto alla superficie della Papalterra. La sua distanza dal baricentro è data da:
s = h + RT + d
Il semiasse dell’orbita as è allora dato da:
2aS = h + RT + d + RT – d = 2RT + h
as = RT + h/2
Bisogna, adesso, trovare il valore di h tale che l’orbita sia rispettosa delle leggi di Keplero e della fisica.
Indichiamo con vM la velocità all’apogeo e applichiamo la seconda legge di Keplero, ossia la conservazione del momento angolare, calcolato al perigeo e all’apogeo (le velocità sono perpendicolari al raggio vettore):
vm (RT – d) = vM (d + RT + h) …. (2)
e imponiamo, anche, la conservazione dell’energia (energia potenziale ed energia cinetica) per gli stessi punti:
- GMm/(RT – d) + ½ m vm2 = - GMm/(d + RT + h) + ½ m vM2
- GM/(RT – d) + ½ vm2 = - GM/(d + RT + h) + ½ vM2 …. (3)
Molto bene…
Dalla (2) possiamo ricavare vM, ossia:
vM = vm (RT - d)/(d + RT + h)
Ma, dalla (1), sappiamo che:
vm = (GMRT)1/2/(RT – d)
per cui :
vM = (GMRT)1/2(RT - d)/((d + RT + h)(RT – d)) = (GMRT)1/2/(d + RT + h)
Non ci resta, adesso, che sostituire vm e vM, così ricavate, nella (3).
Si ottiene:
- GM/(RT – d) + ½ GMRT/(RT – d)2 = - GM/(d + RT + h) + ½ GMRT/(d + RT + h)2
Semplificando (e quindi eliminando le “antipatiche” grandezze M e G), si ha:
- 1/(RT – d) + ½ RT/(RT – d)2 = - 1/(d + RT + h) + ½ RT/(d + RT + h)2
Questa equazione ha una sola variabile, h, dato che RT e d sono noti… Basta, perciò, risolverla, tenendo come buona la soluzione positiva (ovviamente).
Usando qualche trucchetto (ma probabilmente si può fare di meglio), con un po’ di fatica e molta attenzione a non commettere errori di moltiplicazione o cose del genere (io ne ho fatti parecchi prima di arrivare in fondo...), si giunge al seguente risultato:
h = 2d2/(RT – 2d)
Che, con i dati in nostro possesso, risulta:
h = 20000/(6371 – 200) = 3.241 km
Poco più di 3 km sopra la superficie sferica di Papalterra…
Il semiasse dell’orbita (che soddisfa le leggi di Keplero) diventa, quindi:
as = RT + h/2 = 6371 + 1.6205 = 6372.6205 km
Dobbiamo notare che abbiamo usato numeri con cifre significative un po’ saltellati, ma, d’altra parte, possiamo sempre permetterci di fissare arbitrariamente il raggio terrestre e certi altri valori. L’importante è usare sempre gli stessi per potere fare il confronto tra i periodi.
PST è il periodo di un oggetto che circola perfettamente attorno alla vera Terra (liscia) ad altezza uguale a zero (ricavato all’inizio) e PSPAP è il periodo del satellite inserito su Papalterra. Poco importa, però averli ricavati. Basta conoscere i semiasse e applicare la terza legge di Keplero per trovare il rapporto dei periodi:
PSPAP/PST = (aS/RT)3/2 = (6372. 6205/6371)3/2 = 1.0004
Ricapitoliamo: il succo di questo approccio è stato quello di far partire il satellite dal punto più vicino al baricentro, ma con una velocità tale da non farlo mai penetrare all’interno della Papalterra. L’unico modo per far ciò è dargli una velocità pari a quella necessaria a ruotare attorno al centro della sfera. Qualsiasi velocità minore non sarebbe accettabile, dato che il satellite si schianterebbe a terra (ops… a papalterra…).
N.B. (in divenire): la soluzione proposta da Paolo e da Umberto sembrerebbe migliore… Tuttavia, l’ellisse da loro trovata è puramente geometrica e potrebbe non soddisfare la seconda legge di Keplero e la conservazione dell’energia. Bisognerebbe calcolare la velocità al perigeo e all’apogeo e poi fare un po’ di conti… Chi vuole provare ha pane per i suoi denti.
Ancora una volta… stupitemi!!!
Il QUIZ lo trovate QUI (con tutti i fondamentali commenti)
QUI la soluzione definitiva






17 commenti
Caro Enzo ho provato a fare un po’ di conti, ma non sono molto sicuro che l’impostazione sia completamente corretta.
Partendo dall’ellisse che avevo costruito, con il centro in C (centro pianeta) ed uno dei due fuochi in G (centro di gravità) http://www.infinitoteatrodelcosmo.it/2016/10/29/quiz-orbitando-attorno-alla-papalterra/#comment-274576 vediamo cosa succede al momento angolare L ed alla conservazione dell’energia nei due punti dove il satellite risulta più vicino la centro di gravità (E) oppure più lontano da questo (D).
Quando il satellite è più vicino al centro di gravità G (segmento GE), la sua distanza è uguale ad (a – d), dove d è uguale a 100 km (ossia al segmento CG).
Quando è più lontano dal centro di gravita G (segmento GD), la sua distanza è uguale ad (a+d).
Infine per costruzione, il semiasse maggiore dell’ellisse è uguale a:
a = √b² + d² = √R² + d² …dato che per costruzione il semiasse minore b è uguale al raggio della Terra, ossia R.
Il momento angolare si conserva se:
L = m Vm (a-d) = m VM (a+d)
Vm (a-d) = VM (a+d)
Vm/VM = (a+d)/(a-d)
Questo rapporto è costante per cui lo chiamo K
Vm/VM = (a+d)/(a-d) = K
L’energia totale si deve conservare in entrambe le condizioni, per cui:
½ mVm² - GMm/(a-d) = ½ mVM² - GMm/(a+d) divide tutto per m
½ Vm² -½ VM² = GM/(a-d) - GM/(a+d)
½Vm² -½VM² = GM (a+d) – GM (a-d) /(a-d) (a+d)
½ Vm² -½ VM² =GM (a +d -a +d) /(a-d) (a+d)
½ Vm² - ½ VM² = GM (2d) /(a-d) (a+d)
Vm² - VM² = 4 GM d/(a-d) (a+d)
ma a= √R² + d² e Vm= VM k
VM²k² - VM² = 4 GM d/(√(R² + d²) - d) (√(R² + d²) +d)
VM² (k² - 1) = 4 GM d/(R² + d²) - d √(R² + d²) + d √(R² + d²) -d²)
VM² (k² - 1) = 4 GM d/(R² + d²) -d²
VM² (k² - 1) = 4 GM d/R²
VM² = 4 GM d/ R²(k² - 1)
Sostituisco i valori di G, M d R e K
G= 6,67408 x 10^-11
M= 5,97219 x 10^24
GM= 3,98589 x 10^14
D= 100 km = 100000 metri
R = 6371 km = 6371000 metri
R² = 4,05896 x 10^20 metri
(a+d) = 6371,748 + 100 = 6471,748 km = 6471 784 metri
(a-d) = 6371,748 - 100 = 6271,748 km = 6271 784 metri
K = (a+d)/(a-d) = (6471784)/6271 784) = 1,031888853
K²= 1,064794606
(K² -1) = 0,064794606
VM² = 4 GM d/ R²(k² - 1)
VM² = 4 (3,98589 x 10^14) (100 000)/(4,05896 x 10^20) (0,064794606)
VM² = 60622096,92
VM = √60622096,92 = 7786,019325 m/sec
Ora ricavo Vm, usando k:
Vm = k VM = (7786,019325) 1,031888853 = 8034,306553 m/sec
Per verificare se l’Energia si conserva, deve valere che:
½ Vm² - ½ VM² = GM/(a-d) - GM/(a+d)
½ Vm² - ½ VM² = ½ 8034,306553² - ½ 7786,019325² = 1963992
GM/(a-d) - GM/(a+d) = 3,98589 x 10^14/6271 748 - 3,98589 x 10^14/6471 748 = 1963992
Non so se il metodo ed i calcoli sono corretti, però…
Paolo
caro Paolo,
tutto si conserva nei punti estremi, ma ho ancora dei dubbi...
Ho qualche problema sulla velocità nel punto P.
Essa deve essere tangente all'ellisse. Ma, nel tuo caso è anche tangente al cerchio della Terra.
La velocità di un satellite che orbita attorno alla Terra é: v^2 = GM/R
Nel caso della tua ellisse, la velocità deve perciò essere maggiore di questa velocità.
Ma, la velocità in un punto qualsiasi dell'ellisse è data da:
v^2 = GM(2/r - 1/a)
Nel punto P, abbiamo che r = a e quindi nel punto P vale:
vP^2 = GM/a
che risulta minore di quella del moto circolare.... Il che sembrerebbe impossibile...
Forse sbaglio perché sono di fretta.... Dove sbaglio, però????? AIUTO!!!!!!!!!!!!!
qui il discorso è un po' diverso della soluzione di sopra, dove abbiamo un vincolo per la velocità vm imposto dal fatto che il satellite non debba penetrare nella terra; il fatto di aver posto il semiasse minore uguale a Rt e ricavato il semiasse maggiore con Pitagora, ci assicura che geometricamente l'ellisse non interseca la terra; posso dire quindi che le due velocità v1,v2 siano quelle consone a un moto orbitale con tale semiasse, e derivano dalle formule della conservazione dell'energia, con r1,r2 le rispettive distanze radiali:
v1=(2GM(1/r1-1/2a)^1/2
v2=(2GM(1/r2-1/2a)^1/2
quindi impongo queste due velocità, che senz'altro conservano l'energia perchè derivano proprio da essa.
prendendo tali v1,v2 voglio dimostrare che r1*v1=r2*v2
sviluppando i calcoli per r1*v1,r2*v2 ottengo:
r1(2a-r1); r2(2a-r2) sostituendo a r1=a-d, r2=a+d ottengo
(a-d)(2a-a+d); (a+d)(2a-a-d); (a-d)(a+d) che è proprio uguale a (a+d)(a-d)
quindi il momento angolare si conserva. quello che non mi torna è che questo sembra un fatto assolutamente generale
A me, comunque, non torna la velocità nel punto P... a meno che non continui a fare lo stesso errore e non me ne accorga.
vP^2 = GM(2/r - 1/a) = GM/a
dove sbaglio, accidenti????
Non è che la vera ellissi parta dal vostro perigeo e arrivi al vostro apogeo, ma non possa essere tangente in P? Ossia devo allargarla fino a che la velocità in P sia quella calcolata da me (a rimane la stessa). Non so devo pensarci... con calma... O, viceversa, partendo da quel punto ricavo la a...
ma nel punto P r non è a-d ? Ma P nel nostro caso ê esterno al cerchio
r è il raggio vettore, ossia GP, che è a (o mi sbaglio?). La figura mette P sul cerchio... Ci sono infinite ellissi che hanno semiasse = a... basta cambiare la e (ossia b). Solo una è quella fisica....
Umberto... nella figura di Paolo, P NON è il perigeo...
Dunque... cerco di fare una sintesi e cercare tutti assieme come dimostrare che l'approccio non può stare in piedi.
Considerando la figura di Paolo, posso sempre pensare che il satellite venga fatto partire in P. Per farlo sollevare la velocità che devo impartirgli deve essere almeno uguale a quella circolare di centro C, dato che anche quella relativa alla distanza r (PG) deve essere tangente alla circonferenza (il cerchio è il cerchio osculatore dell'ellisse nel punto P). Ne segue che la velocità in P deve almeno essere (ho eliminato il GM in tutte le formule)
vP^2 = 1/R
Non ha quindi alcun senso impartirgli una velocità minore. A questo punto si può costruire l'ellisse del satellite.
Imponendogli l'ellisse definita da Paolo si avrebbe, in P, una velocità
vP^2 = 1/a , sicuramente più piccola di 1/R.
Qualcosa non torna....
Forza: cerchiamo di distruggere questo mio ragionamento o trovare qualcosa di più concreto per distruggere quello di Paolo e Umberto...
Per quanto riguarda il dubbio di Enzo, forse c'è da considerare che nel punto P di Paolo (intersezione dell'ellisse con l'asse minore) l'ellisse è tangente al pianeta , ma non è tangente ad un orbita circolare intorno al centro di massa.
-----
Nella verifica della fisicità della soluzione di Paolo ho imposto il raggio di curvatura al perigeo ed apogeo. Enzo ha imposto che nei due punti il raggio sia R, perchè nel caso visto sopra l'ellisse nei due punti è tangente alla Terra, cosa che non è applicabile alla soluzione di Paolo. Avevo notato smanettando con il problema che la derivata seconda dell'ellisse (-a/b^2) in quel punto è proprio -1/R nel caso esaminato da Enzo. Assumo allora che in generale il raggio di curvatura al perigeo ed apogeo sia b^2/a, che nel caso di Paolo però non è uguale a R ma è R^2/sqrt(R^2+d^2).
Da questo verrebbe che l'uguaglianza dell'attrazione gravitazionale con la forza centrifuga dia:
GM/(a-d)^2=vm^2 a/b^2 ==> vm^2=GM/(a-d)^2 b^2/a
GM/(a+d)^2=vM^2 a/b^2 ==> vM^2=GM/(a+d)^2 b^2/a
( a e b sono i semi-assi maggiore e minore).
Che coincide con quanto trovato da Umberto.
Questi vm e vM mi sembrano coerenti sia con la conservazione dell'Energia sia con la conservazione del momento angolare come ha verificato Umberto.
Quindi l'orbita di Paolo richiederebbe al perigeo vm=sqrt(GM/(a-d)^2 b^2/a) con a=sqrt(R^2+d^2) e b=R e tutto il resto sembrerebbe coerente.
Sono rimasto sorpreso come Umberto che questo accada, ma forse è proprio per queste coincidenze che la soluzione dell'orbita di un satellite è un ellisse con il centro di massa nel fuoco.
caaro Fabry,
continua a non convincermi del tutto... Magari bisognerebbe calcolare anche il momento angolare nel punto P...
Il procedimento usato da me, in fondo, impone solo che il perigeo sia il punto di minima velocità per non scontrarsi con la Terra. Poi, solo dopo, se ne deriva il semiasse, basandosi solo sulla seconda legge... Nel caso di Paolo si impone a priori sia il perigeo che il semiasse... E' veramente corretto?
Vorrei darvi ragione, ma mi vedo male un satellite sparato da p che riesca a mettersi in orbita...
Caro Enzo, mi sa che hai ragione tu.
Se fisso un eguale momento angolare per il punto P rispetto al punto E o al punto D non si conserva l'Energia Totale.
Riporto la figura con i vari punti.
Usiamo il punto D per fare il confronto.
L= m VM (a+d) = m Vp a
VM (a+d) = Vp a
Vp/VM = (a+d)/a = k
Quindi, per quseti due punti (P e D) il rapporto costante k = 1,0156941899
Vp = k VM
Prima avevo ricavato che VM = 7786,019325 m/sec
Vp = k VM = 7908,2150756933 m/sec
Questa è la velocità Vp necessaria per mantenere il momento angolare costante.
Oltre a ciò deve, però conservarsi anche l'Energia Totale:
½ m Vp² – GMm/a = ½ m VM² – GMm/(a + b)
tolgo m ed eseguendo i calcoli ottengo:
½ Vp² – GM/a = ½ 7908,2150756933² - 3,98589 x 10^14 /6371 784 = -31285340,68
½ VM² – GM/(a+d) = 7786,019325² - 3,98589 x 10^14 /6471 784 =-31277636,76
L'Energia Totale nei due punti è diversa...e purtroppo la scaltra ellisse trovata sembra non andar bene … peccato!
Paolo
Se il satellite in P ha una velocità (GM/a)^(1/2) e sta percorrendo una traiettoria che istantaneamente ha raggio di curvatura a^2/b (derivata seconda di y=b(1-x^2/a^2)^(1/2), la componente lungo l'asse minore dell'ellisse della forza verso il centro di massa dovrebbe essere (GmM/a) (b/a^2)=GmM R/a^3.
Se proietto la forza di attrazione GmM/a^2 lungo il semi-asse minore ottengo (GmM/a^2)*(R/a)=GmM R/a^3 che è quella che serve.
Anche l'energia totale in P dovrebbe essere m/2 GM/a - GMm/a=-GMm/(2a)
al perigeo m/2 GM (a+d)/[(a-d)a]- GMm/(a-d)=GMm/(a-d) [(a+d-2a)/2a=-GMm/(2a)
Andare contro l'intuizione del maestro non porta bene, ma questo è quello che ho trovato.
anche se vado contro la mia soluzione, devo dire che Paolo ha calcolato male il momento angolare in P . Mi sa che si è perso un seno per strada (la velocità non è perpendicolare a PG)....
. Mi sa che si è perso un seno per strada (la velocità non è perpendicolare a PG)....
cari tutti (o quasi)...
sono una testa dura e vorrei trovare la soluzione in modo diverso, ossia costruendo un moto ellittico a partire da un perigeo variabile a distanza p da G.
Dato un perigeo si può imporre la velocità che si vuole a patto che siano mantenute le conservazioni di momento angolare e energia. Inoltre per ogni perigeo si deve prendere l'ellisse che sia tangente esternamente alla Terra (non si può attraversare). Il problema dovrebbe essere esprimibile in funzione di p e di a. Avremo una famiglia di ellissi funzioni di a e p. Quella con a minore sarebbe quella da scegliere.
Il caso limite è il mio, ossia quello in cui il perigeo è proprio sulla Terra. Allontanando il perigeo le soluzioni sono tante, ma ogni volta si considera solo quella in cui la velocità al perigeo permetta la tangenza e non l'attraversamento o traiettorie più ampie. Ognuna di queste avrà la sua a.
Senza imposizioni preliminari su a, si dovrebbe comunque trovare la vostra "a" come quella minima. Minima a vuole anche dire minimo periodo.
Purtroppo, mi aspettano tre giorni infuocati (amici in visita) e sono già intruppato con la curvatura, ma posso fidarmi di voi , ormai più che in grado di superarmi con facilità. Avete voglia di provarci?
Consiglierei di eliminare GM, dato che è sempre lo stesso e si deve eliminare comunque (vedi il caso trattato da me...).
volevo solo dire che ho calcolato il momento angolare nel punto P e risulta ((a^2-d^2) *GM/a)^1/2, come in apogeo e perigeo
e, allora, mi sa che mi devo arrendere... anche se quel satellite che arriva in picchiata e sfiora la Terra per poi andarsene mi fa un po' paura