05/11/16

Soluzione definitiva (?) del satellite attorno a Papalterra ***

Categorie: Meccanica Celeste Tags: orbita satellite Papalterra periodo minimo quiz soluzione Scritto da: Vincenzo Zappalà Commenti:37

Cari amici, è con vero piacere che devo ammettere di essere caduto, relativamente al quiz sul satellite della Papalterra (QUI e QUI), in uno di quegli errori di cui avevamo parlato nel famoso QUIZ della formica sul barattolo. Ho considerato un caso limite come soluzione minima senza tener conto di tutta una serie di possibilità. Devo dire grazie a Paolo, Umberto e Fabrizio per avermi messo con le spalle al muro. Questo è il bello di questo Circolo, dove chiunque può sbagliare e tutto serve per continuare a imparare e mettersi alla prova, con allegria e umiltà.

Cito una frase che avevo scritto nella soluzione del quiz della formica e del barattolo : “In realtà, si era arrivati alla conclusione senza tener conto delle vie alternative e senza valutare se potessero essere le più corte. In altre parole ci siamo limitati a guardare i due estremi di una funzione, senza curarci di cosa faceva tra uno e l'altro. Questo esempio, non certo banale, vuole solo mettere in guardia di fronte a soluzioni apparentemente semplici e rapide. Vale sempre la pena di ragionarci un po’ sopra. Di questi tempi, dominati dalla fretta e da pressapochismo, questo articolo può essere veramente utile.”

Bene… temo di essere caduto proprio nell’errore da cui, con un po’ di “spocchia”, avevo cercato di tenervi alla larga. Ben mi sta!

A parte gli scherzi… ne sono proprio contento, perché questo fatto ribadisce il valore di molti lettori e la loro attenzione estrema nell’affrontare gli argomenti trattati. Facendo il “mea culpa” lasciatemi, però, sperare che essere riusciti ad avere lettori, così pronti e preparati, sia un po’ anche merito di questo Circolo che sta arrivando proprio dove avrei voluto potesse arrivare, qualche anno fa. Un gruppo di persone che vogliono ancora far lavorare il proprio cervello e che danno il giusto rilievo a tutto ciò che la Scienza ci ha insegnato finora. Un gruppo che collabora attivamente… che bello!

No, non sto cercando di addolcire la pillola che ho ingoiato con grande soddisfazione (credetemi!) e passo subito al sodo.

Vediamo se riesco a esprimere meglio il problema generale. Uso la Fig. 1 (molto rozza e solo qualitativa) per cercare di riassumere le idee, che potrebbero non essere ancora del tutto esatte.

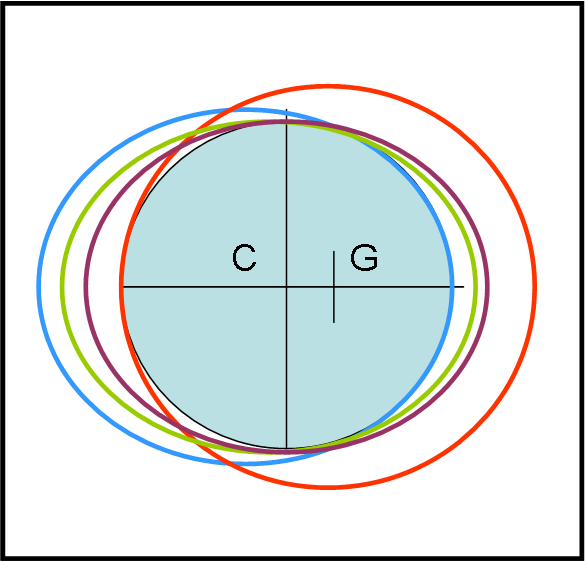
Vogliamo inserire un satellite nell’orbita più rapida attorno a un centro di gravità G, che però ha il problema di avere attorno a sé una sfera solida che blocca certe traiettorie. Non solo: il centro di gravità non coincide con il centro della sfera. Fossero coincidenti, l’orbita più rapida (periodo minore) sarebbe quella che segue perfettamente la superficie della sfera (considerata liscia e senza attriti).

A questo punto, abbiamo pochi gradi di libertà nel tracciare orbite plausibili, che siano le più rapide e sfiorino soltanto l’ingombrante sfera.

Ad esempio, l’orbita rossa, in cui si è considerato una circonferenza di centro G che tocchi la Papalterra nel punto più lontano da G è una soluzione plausibile, ma non è un minimo (il primo tentativo di Paolo).

Io, invece, ho considerato il caso limite opposto, ossia quello di prendere come perigeo il punto della sfera più vicino a G. In altre parole, la traiettoria tocca la sfera nel suo punto più vicino a G (orbita azzurra). Questa soluzione potrebbe sembrare la migliore (e così ho pensato anch’io), ma ha un problema non indifferente. Non posso dare una qualsiasi velocità al perigeo, altrimenti la traiettoria entrerebbe all’interno della sfera. E lì ho commesso l’errore… Ho considerato comunque questa orbita come la più rapida. E, invece, potrebbero esserci dei casi intermedi più interessanti e… rapidi. Ad esempio, le orbite viola e verde

Esse hanno lo svantaggio di avere un perigeo più lontano dal centro di gravità, ma non sono bloccate nel valore della velocità in quel punto (o, almeno non sempre). Esse potrebbero sfiorare la Papalterra in punti diversi ed essere completamente plausibili oltre che più rapide.

In altre parole, costruendo le ellissi che abbiano un perigeo variabile, con una velocità tale da fare toccare al satellite la sfera solida, ma senza penetrarvi all’interno, avremmo una certa funzione del semiasse in funzione del perigeo, che potrebbe (e sembra proprio che ce l’abbia) un minimo che non coincide con gli estremi.

Questo, secondo me, sarebbe il miglior modo per affrontare il problema (meglio tardi che mai…) e si dovrebbe trovare come minimo proprio quello prospettato dallo stesso Paolo, da Umberto e da Fabrizio. Ovviamente le orbite devono essere fisicamente accettabili, ossia devono mantenere la costanza del momento angolare e dell’energia (relazioni che servono anche per determinare la geometria finale). Mi sembra un approccio corretto, ma aspetto anche le vostre reazioni a proposito…

Invito i “magnifici tre”, ma anche altri finora silenziosi, a cercare di seguire questo approccio (o quello che preferiscono se ne trovano uno di migliore), dato che l’aver scelto a priori il semiasse di quella che potrebbe essere la soluzione migliore non mi piace tanto… Consiglio anche di non fare calcoli numerici inutili: in fondo servono solo i valori di a da confrontare tra di loro. Potete, perciò, eliminare sempre e comunque GM, dato che la massa e la costante sono sempre le stesse…

Mettete in moto le vostre menti e poi potrete pubblicare ufficialmente il risultato che sono sicuro riuscirete a trovare. Se non è collaborazione questa…

Intanto vi ringrazio di vero cuore e mi immergo nella curvatura dello spazio a tre dimensioni per renderlo il più chiaro possibile. I lettori di questo Circolo se lo meritano sicuramente!

37 commenti

Umberto

09/11/2016 at 07:25

Provo a scrivere una soluzione generale; mi baso su questo disegno che rappresenta le ellissi con fuoco in G, però scritte in formula rispetto al centro degli assi;di conseguenza sarà variabile il centro C della circonferenza.

Dobbiamo trovare un valore minimo per il semiasse maggiore. che corrisponde per la terza legge di Keplero con un periodo minimo.

equazione circonferenza con centro in C:

$(x-c)^{2}+y^{2}=R^{2}$

equazione canonica dell'ellisse con centro negli assi:

ponendo c+d=e,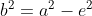 $b^{2}=a^{2}-e^{2}$ ,

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-e^{2}}=1$ ; queste sono tutte le possibili ellissi con fuoco in G.

Un orbita ellittica è possibile se il centro di gravità G coincide con il fuoco dell'ellisse.

Limitiamoci al semipiano positivo delle y (possiamo farlo per questioni di simmetria); affinchè la semi-ellisse contenga la semi-circonferenza, deve essere:

$(1-\frac{x^{2}}{a^{2}})(a^{2}-e^{2})\geq R^{2}-(x-c)^{2}$

(l'eguaglianza è nei punti di tangenza)

dopo calcoli abbastanza mostruosi che vorrei evitare si arriva alla disequazione di secondo grado: $x^{2}\cdot \frac{e^{2}}{a^{2}} -2xc + a^{2}-e^{2}-R^{2}-c^{2}\geq 0$

questa è una parabola rivolta verso l'alto (il coefficiente di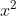 $x^{2}$ è positivo) ; studiamo il discriminante :

$\Delta =c^{2}-\frac{e^{2}}{a^{2}}\cdot (a^{2}-e^{2}-R^{2}-c^{2})$ ; ponendo $\Delta =0$ (in tal modo essendo la parabola rivolta verso l'alto e l'intersezione con l'asse delle x unica, essa risulta sempre >=0 )e sostituendo a e=c+d; otteniamo una espressione per a (semiasse maggiore) in funzione di c; ricordiamo che R,d sono parametri costanti.

$a=\sqrt{\frac{-R^{2}-a^{2}-d^{2}-2cd}{c^{2}-1}}$ ; abbiamo dunque che a è funzione di c.

si tratterà di trovare un minimo per questa funzione, di cui ho tracciato il grafico;

essa assume il minimo per c=0, dove a vale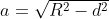 $a=\sqrt{R^{2}-d^{2}}$ , e che corrisponde alla soluzione ipotizzata .
Vincenzo Zappalà

09/11/2016 at 09:00

Fantastico Umberto... sei proprio di un altro livello. Il Circolo ti ringrazia di vero cuore. Se ne hai voglia (e lo spero veramente) potresti riportare la descrizione (magari con qualche passaggio in più) come articolo che avrà come titolo proprio la soluzione definitiva, senza più punti interrogativi!

Un abbraccio da parte di tutti noi. Questa è vera collaborazione... sono commosso... ve lo assicuro...

GRAZIE INFINITE !!!!
Umberto

09/11/2016 at 10:36

Troppo buono! Comunque va bene, cercherò di completarlo.
Vincenzo Zappalà

09/11/2016 at 10:43

caro Umberto,

controlla bene i passaggi finali, sembra che ci sia una "a" ballerina nella funzione... E il risultato è poco intuitivo...
Umberto

09/11/2016 at 10:49

segnalo un errore di stampa; la funzione finale corretta è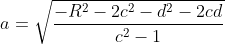 $a=\sqrt{\frac{-R^{2}-2c^{2}-d^{2}-2cd}{c^{2}-1}}$

sto preparando però un articolo con tutti i passaggi esplicitati, compreso lo studio del minimo tramite derivata prima e insieme di definizione
Vincenzo Zappalà

09/11/2016 at 10:50

Ho provato a prendere per buona la relazione:

$a=\sqrt{\frac{-R^{2}-a^{2}-d^{2}-2cd}{c^{2}-1}}$

se elevo a quadrato, ottengo

a2c2 -a2 = -R2 -a2 -d2 -2cd

a2 = ( -R2 -a2 -d2 -2cd)/c2

ossia

a = sqrt((-R2 -a2 -d2 -2cd)/c2)

che per c=0 va a infinito...

c'è qualcosa che non torna... o sbaglio?
Vincenzo Zappalà

09/11/2016 at 10:53

Non va ancora bene Umberto, perché il risultato sarebbe

a = sqrt( +R2 + d2) ....
Umberto

09/11/2016 at 11:08

quella che hai preso per buna è sbagliata; ho riportato un a^2 mentre in realtà era un 2 c^2

$a=\sqrt{\frac{-R^{2}-2c^{2}-d^{2}-2cd}{c^{2}-1}}$ questa è quella giusta, però devo fare i calcoli della deerivata
Vincenzo Zappalà

09/11/2016 at 11:44

Sì, ma per c=0 non viene il risultato voluto... ma:

a = sqrt(+R2 + d2)
umberto

09/11/2016 at 12:05

hai ragione, c ê un altro errore di stampa sopra perché nella soluzione di Paolo a ê proprio sqrt(R2 più d2)
Fabrizio

09/11/2016 at 13:47

Con un procedimento simile a quello di Umberto a me era venuto:

a(c)=(c+d)sqrt(1+R^2/(d(2c+d))

Che ha come minimo

c=(R sqrt(R^2+8d^2)-(R^2+4d^2))(8d)

Con i valori numerici del quiz c=-24,6m, molto vicino allo 0.

In effetti le ellissi tangenti sono tutte molto simili tra loro, l'asse maggiore varierebbe di meno di 840m per i valori numerici del quiz spostando il punto di tangenza da perigeo al minimo. Il valore dell'asse maggiore al minimo differirebbe da quello di Paolo di neanche un metro.

Questo se non ho commesso errori, che facilmente ci possono essere per la difficoltà dei passaggi.

Sto preparando una risposta con i dettagli e con le formule più visibili, dove sto mettendo anche un ragionamento sulla validita fisica di queste orbite.

Fabrizio
Vincenzo Zappalà

09/11/2016 at 14:39

In realtà sqrt(R2 + d2) mi torna con la soluzione di Paolo.

Dai vediamo chi ha ragione tra Umberto e Fabrizio: che bella lotta!!!!

Comunque sia, bravi tutti e due che ci stanno provando alla grande!
Fabrizio

09/11/2016 at 16:33

Questo è il mio tentativo di seguire, almeno parzialmente, il percorso indicato da Vincenzo. Nessuna lotta con Umberto. Anzi cito più avanti, non so se propriamente, uno dei suoi articoli che leggo con molto interesse .

Se non ho fatto errori, facilmente possibili per la complessità dei passaggi, qualche piccola sorpresa sul posizionamento del minimo, il metodo indicato da Vincenzo l'ha portata. Il minimo è diverso da quelli finora considerati, ma vicinissimo a quello di Paolo. In effetti le ellissi tangenti sono tutte molto simili tra loro, l'asse maggiore varia meno di 840m per i valori numerici del quiz.

Le espressioni trovate sono queste:

Di seguito il procedimento seguito ed un ragionamento sulla validità fisica delle ellissi trovate.
Vincenzo Zappalà

09/11/2016 at 16:37

caro Umberto,

ho trovato un altro errorino ( così mi sembra)

tu scrivi:

$b^{2}=a^{2}-e^{2}$

invece dovrebbe essere :

b2 -a2 -a2e2

b = a sqrt(1 - e2)
Vincenzo Zappalà

09/11/2016 at 16:58

Dando un'occhiata, sono d'accordo con l'ellisse e la circonferenza di Fabrizio... cerco di andare avanti tra uno spaziotempo e un altro...
Umberto

09/11/2016 at 17:14

quella e è c+d, non c'entra con l'eccentricità
Vincenzo Zappalà

09/11/2016 at 18:06

ah... OK, OK... solo che mi ha creato confusione...

tra parentesi c può essere messo in funzione della distanza perielica, ma va bene lo stesso...

Così a occhio direi che le due curve sembrano giuste (tua e di Fabry).

bisognerebbe controllare i due discriminanti...
Vincenzo Zappalà

09/11/2016 at 18:13

per Fabry... scusa, ma non basta trovare il valore di a minore? E' quello che darà anche il periodo minore...ma forse mi sono perso un po'... non riesco a fare due cose contemporaneamente...
Fabrizio

09/11/2016 at 18:23

Credo di avere trovato proprio il valore di a minimo ed il valore di x_0 al quale avviene trovando le soluzioni di ${\frac{\mathrm{d }\, a(x_0)}{\mathrm{d} x}}=0$ .
Fabrizio

09/11/2016 at 18:25

Scusa, di ${\frac{\mathrm{d }\, a(x_0)}{\mathrm{d} x_0}}=0$
Umberto

09/11/2016 at 18:31

sto ricontrollando tutti i calcoli, devo esprimere quel minimo
Vincenzo Zappalà

09/11/2016 at 18:43

le vostre curve sembrano uguali e dovreste trovare lo stesso minimo... Sarebbe bene che usaste la stessa variabile in modo da semplificare il confronto. Dai, sono sicuro che salterà fuori il perché della differenza trovata...

State lavorando duro, ma il risultato è vicino...
Fabrizio

10/11/2016 at 00:11

Caro Vincenzo,

dalla tua domanda capisco che per inseririre troppi dettagli ho fatto perdere il senso del mio intervento. Cerco di esprimerlo più brevemente.

La relazione tra posizione del centro del pianete e lunghezza del simi-asse maggiore dell'orbita ellittica quando l'orbita è tangente al pianeta a me è risultata essere: $a(x_0)=(x_0+d)\sqrt{1+ \frac{R_T^2}{d(2x_0+d)}}$

Questa relazione può essere ottenuta imponendo che i punti di incontro tra circonferenza ed ellisse abbiano la stessa coordinata x.

Il minimo di questa funzione si trova per un valore di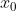 $x_0$ che annulla la derivata di questa funzione. La derivata è piuttosto complessa:

$\frac {{\mathbf{d}} a(x_0)} {\mathbf{d}~ { {x_0}}}=\sqrt{1+\frac{R_T^2 } {{d(2x_0+d)}}}-(x_0+d) \frac{R_T^2} {d (2 x_0+d)^2 \sqrt{1+\frac{R_T^2 } {d(2x_0+d)}}}=0$

che equivale alla equazione di 2° grado:

$4\, d\, x_0^2+(R_T^2+4 d^2)x_0+d^3=0$

Il minimo si trova in una delle due soluzioni

$x_0=\frac{-(R_T^2+4 d^2)+R_T \sqrt{(R_T^2+8 d^2)} } {8 d}$

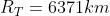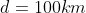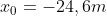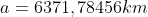Il corrispondente valore di a si ottiene inserendo il valore ottenuto nella $a(x_0)$ vista sopra. Per $R_T=6371km$ e $d=100km$ si ottiene $x_0=-24,6m$ corrispondente ad $a=6371,78456km$ .

La validità fisica di questa soluzione, come delle altre ellissi con fuoco nel centro di massa del pianeta, credo sia verificabile dimostrando che per ciascuna di queste ellissi esistono una posizione iniziale e una velocità iniziale che fa percorrere al satellite l'ellisse.

Dicevo come sintesi: se ogni orbita (chiusa) è una ellisse con fuoco nel centro di massa, ogni ellisse con fuoco nel centro di massa può essere un'orbita?

Provo a dimostralo invertendo le relazioni che portano dalle condizioni iniziali all'orbita passando per l'energia totale (E) ed il momento angolare (L).

Se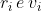 $r_i\, e\, v_i$ sono posizione rispetto al centro di massa e velocità iniziali, che per semplicità scelgo ortogonali, allora:

$E=\frac{1} {2} m v_i^2-m \frac{GM} {r_i}$ $L=m r_i v_i$ da queste si possono ricavare i valori del semi-asse maggiore (a) e minore (b)

$a=- \frac{mGM} {2 E}$ $b= \frac{L} { \sqrt{-2 E m} }$

Se inverto queste relazioni ottengo:

$r_i=a-\sqrt{(a^2-b^2)}$

$v_i=\pm \sqrt{\frac {GM} {a} \left (\frac{{ a+\sqrt{(a^2-b^2)}}} {a-\sqrt{(a^2-b^2)}} \right ) }$

Poichè da queste equazioni non possono risultare immaginari o divisione per 0, per ogni coppia a, b esistono le opportune condizioni iniziali, quindi tutte le ellissi possono avere una validità fisica.
Vincenzo Zappalà

10/11/2016 at 05:39

Ottimo riassunto... e perfetto il test "fisico".

Appena alzato mi chiedevo, ma devo controllare, perchè non imporre come origine degli assi il centro del cerchio? Esso è qualcosa di fisso che si può rappresentare con la semplice funzione:

x2 + y2 = R2

Non è difficile esprimere l'ellisse rispetto a questo punto in modo che compaiano solo a e il centro dell'ellisse e poi imporre la tangenza...

Devo andare a controllare se avete fatto così... ieri ero inc... ato al massimo. Stamattina cerco di ragionarci con calma...
Umberto

10/11/2016 at 06:37

all'inizio avevo provato così, con il cerchio al centro degli assi; ma i conti venivano ancora più complessi
Vincenzo Zappalà

10/11/2016 at 06:54

In realtà i conti sono solo noiosi e lunghi e si rischia di fare errorini di scrittura... Adesso voglio provare a calcolarla io scegliendo le tue coordinate, in modo che sia più facile fare confronti...

a dopo...
Umberto

10/11/2016 at 07:29

Ho rifatto più volte i conti; quello che ho controllato più volte è questo risultato:

$a(c)=(c+d)\cdot \sqrt{\frac{ (d^{2}+2dc+R^{2})}{d(2c+d)}}$

(i conti alla fine del commento)

che è uguale al tuo (non riuscivo a capirlo perchè era scritta diversa)

penso sia giusto perchè per c=0 deve dare la soluzione del cerchio centrato con l'ellisse che viene proprio , per c=0, $a(0)=\sqrt{d^{2}+R^{2}}$ .Bisognerebbe verificare se contempla anche la soluzione di Vincenzo. Studiata con desmos la funzione dà un minimo, che però non è zero. Se mi permetti di usare la tua derivata (per un po' di tempo giuro che non farà piu conti di questo tipo), essa non si annulla in zero;

Questo mi fa concludere che quello che ho sempre sostenuto, ovvero la soluzione provvisoria, non sia valida; Essa si ottiene infatti per c=0, ma zero non è un minimo. Hai fatto bene Vincenzo a proporre questo sistema. Bisognerebbe anche vedere graficamente dove si colloca questa ellisse.

studiamo il discriminante :

$\Delta =c^{2}-\frac{e^{2}}{a^{2}}\cdot (a^{2}-e^{2}-R^{2}-c^{2})$ ; ponendo $\Delta =0$ (in tal modo essendo la parabola rivolta verso l'alto e l'intersezione con l'asse delle x unica, essa risulta sempre >=0 )e sostituendo a e=c+d; otteniamo una espressione per a (semiasse maggiore) in funzione di c;

$c^{2}-\frac{e^{2}}{a^{2}}\cdot (a^{2}-e^{2}-R^{2}-c^{2})=0$

moltiplichiamo per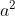 $a^{2}$ :

$a^{2}c^{2}- e^{2}\cdot (a^{2}-e^{2}-R^{2}+c^{2})=0$

$a^{2}c^{2}= e^{2}\cdot (a^{2}-e^{2}-R^{2}+c^{2})=0$

$a^{2}c^{2}-e^{2}a^{2}= e^{2}(-e^{2}-R^{2}+c^{2})=0$

$a^{2}(c^{2}-e^{2})= e^{2}(-e^{2}-R^{2}+c^{2})$

$a^{2}=\frac{ e^{2}(-e^{2}-R^{2}+c^{2})}{(c^{2}-e^{2})}$

$a^{2}=\frac{ (c+d)^{2}(-(c+d)^{2}-R^{2}+c^{2})}{(c^{2}-e^{2})}$

$a^{2}=\frac{ (c+d)^{2}(-c^{2}-d^{2}-2dc-R^{2}+c^{2})}{(c^{2}-e^{2})}=\frac{ (c+d)^{2}(-d^{2}-2dc-R^{2})}{(c^{2}-e^{2})}$

$c^{2}-e^{2}=c^{2}-(c+d)^{2}=c^{2}-c^{2}-2cd-d^{2}=-d(2c+d)$

$a^{2}=\frac{ (c+d)^{2}(-d^{2}-2dc-R^{2})}{-d(2c+d)}$

$a=(c+d)\cdot \sqrt{\frac{ (-d^{2}-2dc-R^{2})}{-d(2c+d)}}$

$a(c)=(c+d)\cdot \sqrt{\frac{ (d^{2}+2dc+R^{2})}{d(2c+d)}}$

$a(0)=\sqrt{d^{2}+R^{2}}$
Umberto

10/11/2016 at 08:46

mi sono dimenticato di specificare che l'ultimo commento era rivolto principalmente a Fabrizio; adesso che siamo (quasi) certi che la funzione è quella giusta, proverò a studiarla in rigorosamente
Vincenzo Zappalà

10/11/2016 at 08:54

Senza guardare gli ultimi aggiornamenti, ho voluto svolgere il problema in modo indipendente e vedere se i conti tornano con quelli di Umberto e Fabry.

Consideriamo come origine il centro dell’ellissi generica.

La figura è quindi quella di Umberto

x²/a²+ y²/b² = 1

sappiamo anche però che:

OG = c + d

Da cui:

b² = a² – (c + d)²

Ponendo e = c + d

Si ha:

b² = a² – e²

da cui:

x²/a²+ y²/(a² – e²) = 1 …. (1)

La circonferenza di centro C (OC = c) ha equazione:

(x – c)² + y² = R² …. (2)

Facendo sistema tra (1) e (2) trovo le intersezioni tra ellissi e circonferenza

(x – c)² + y² = R²

x²/a²+ y²/(a² – e²) = 1

Ricavo y² dalla prima e lo sostituisco nella seconda:

y² = R² – (x-c)²

x²/a²+ (R² – (x-c)² )/(a² – e²) = 1

questa è l’equazione che ci deve dare le ascisse delle intersezioni, se esistono, tra ellissi e cerchio.

Svolgiamola per bene:

x²(a² – e²) + a²(R² – (x-c)²) = a²(a² – e²)

x²a² – x² e² + a²R² – a²x² - a²c² + 2a²xc - a⁴ + a²e² = 0

semplificando x²a²

si ottiene:

- e²x² + 2 a²xc + a²R² - a²c²- a⁴ + a²e² = 0

Cambiamo di segno:

e²x² - 2 a²xc - a²R² + a²c²+ a⁴ - a²e² = 0

A noi interessa solo il caso in cui le due curve siano tangenti, ossia che la soluzione sia unica. Questo si ottiene ponendo uguale a zero il discriminante di un’equazione di secondo grado ridotta:

a⁴c² – e²(- a²R² + a²c²+ a⁴ - a²e²) = 0

a⁴c² + e²a²R² – e²a²c² –a⁴e²+ a²e⁴ = 0

a²(a²c² + e²R² – e²c² – a²e² + e⁴) = 0

a non può essere uguale a zero, quindi:

a²c² + e²R² – e²c² – a²e² + e⁴ = 0

e è funzione di c e d, d è noto, R è noto. La funzione precedente vede a come funzione della sola c.

a²(c² – e²) = e²c² – e²R² –e⁴

La funzione va esplicitata in a:

a² = (e²c² – e²R² – e⁴)/( c² – e²)

Poniamo, finalmente, (c + d) al posto di e

a² = e²(c² – R² – e²)/(c² – e²)

a = e ((c² –R² – e²)/(c² – e²))^1/2

Prendiamo solo il segno più dato che a deve essere positiva

Poniamo, finalmente, (c + d) al posto di e

a = (c + d)((c² – R² – (c + d)²)/(c² – (c + d)²)^1/2

a = (c + d)((c² – R² – c² – d² – 2dc)/(c² – c² – d² – 2dc))^1/2

a = (c + d)((R² + d² + 2dc)/(d² + 2dc))^1/2

Questa sarebbe la funzione di cui si deve trovare il minimo…

Ovviamente, per

c = 0

vale a = (R² + d²)^1/2

Non mi trovo con la funzione di Umberto, ma potrebbero anche essere le stesse manovrandole un po'

Prendiamo quella di Fabrizio:

a = (c + d) (1 + R²/(d(2c + d)))^1/2

che sviluppandola, diventa:

a = (c + d) ((d(2c + d) + R2)/(d(2c +d))^1/2

a = (c + d) ((2dc + d² + R²)/(2dc + d²))^1/2

Che è perfettamente quello che ho trovato io…

A questo punto tutto sta nel calcolo della derivata prima per trovare il minimo di a…

NEW: Anche Umberto ha trovato lo stesso risultato e quindi ormai siamo tutti e tre d'accordo sulla funzione di cui va trovato il minimo...

Con calma controllo la derivata e vediamo se si arriva allo stesso risultato...

Piano piano arriviamo tutti e tre allo stesso risultato... Forza miei prodi!!!!
Vincenzo Zappalà

10/11/2016 at 09:03

cari Umby e Fabry... visto che voi riuscite a fare velocemente le derivate con programmini vari, mi fido di voi (dovete trovare lo stesso risultato però...). Per vedere come si sistema è semplice. Dato il valore di a minimo si ottiene facilmente la posizione del perigeo rispetto alla circonferenza, conoscendo d, c e R...

Si accettano scommesse...

Io torno a curvare lo spaziotempo....
Umberto

10/11/2016 at 10:28

in realtà i programmini studiano la funzione numericamente.. comunque la sto studiando in modo classico. grazie per aver verificato i calcoli.
Vincenzo Zappalà

10/11/2016 at 10:51

dovere Umberto! Desidero che siate voi a trovare il risultato finale, avendo fatto tutto il lavoro e seguito perfettamente la mia proposta...
umberto

10/11/2016 at 12:16

ti dirò la verità, se non fosse intervenuto Fabrizio probabilmente avrei lasciato là..odio fare questo tipo di calcoli, mi ricordano la prima superiore..comunque sto mettendo giú formalmente il tutto. Purtroppo ( o per fortuna) il sogno di Hilbert di affidare tutta la matematica ai calcolatori é fallito.. In ogni caso a noi sarebbero rimasti il paradiso di Cantor e quello di Einstein..
Vincenzo Zappalà

10/11/2016 at 14:52

ti capisco, ti capisco... godiamoci, comunque, certi paradisi incontaminati (anche se qualcuno cerca di imbrattarli con frasi senza senso...)
Umberto

10/11/2016 at 17:33

riporto lo studio della funzione; la derivata e i calcoli parziali coincidono con Fabrizio

Per studiare la funzione, la riscrivo in funzione di x:

$a(x)=(x+d)\cdot \sqrt{\frac{ (d^{2}+2dx+R^{2})}{d(2x+d)}}$

la funzione è definita per

inoltre deve essere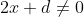 $2x+d\neq 0$ ovvero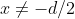 $x\neq -d/2$

il numeratore è positivo per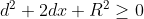 $d^{2}+2dx+R^{2}\geq 0$

ovvero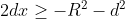 $2dx\geq -R^{2}- d^{2}$

$x\geq \frac{-R^{2}- d^{2}}{2d}$ ,

il denominatore è positivo per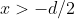 $x>-d/2$ , il segno del rapporto sarà negativo quando i segni sono diversi, , quindi in $\frac{-R^{2}- d^{2}}{2d}\leq x<- \frac{d}{2}$ la funzione non è definita

considero il limite $lim_{x \to 0^{+}} a(x)=lim_{x \to 0^{+}}(x+d)\cdot \sqrt{\frac{ (d^{2}+2dx+R^{2})}{d(2x+d)}}=+\infty$

per x>-d/2 la funzione è positiva, e a noi interessa questo, essendo a un valore positivo.

$lim_{x \to +} a(x)=lim_{x \to +\infty}(x+d)\cdot \sqrt{\frac{ (d^{2}+2dx+R^{2})}{d(2x+d)}}=+\infty$

scrivo la funzione come Fabrizio , dividendo per d(2x+d):

$a(x)=(x+d)\cdot \sqrt{1+\frac{ R^{2}}{d(2x+d)}}$

$Da(x)=\sqrt{1+\frac{R^{2}}{d(2x+d))}}-(x+d) \frac{R^{2}}{d(2x+d)^{2}\sqrt{1+\frac{R^{2}}{d(2x+d))}}}$

(derivata di un prodotto)

poniamo Da(x)=0

$\sqrt{1+\frac{R^{2}}{d(2x+d))}}-(x+d) \frac{R^{2}}{d(2x+d)^{2}\sqrt{1+\frac{R^{2}}{d(2x+d))}}}=0$

$d(2x+d)^{2}\sqrt{1+\frac{R^{2}}{d(2x+d))}})\sqrt{1+\frac{R^{2}}{d(2x+d))}}-(x+d) R^{2}=0$

$d(2x+d)^{2})<span class='MathJax_Preview'><img src='http://www.infinitoteatrodelcosmo.it/wp-content/plugins/latex/cache/tex_b34bb6ae07fa5bf3a625a405fe38b648.gif' style='vertical-align: middle; border: none; ' class='tex' alt=$ {1+\frac{R^{2}}{d(2x+d))}})-(x+d) R^{2}=0" />

$d(2x+d)^{2})<span class='MathJax_Preview'><img src='http://www.infinitoteatrodelcosmo.it/wp-content/plugins/latex/cache/tex_1e15630045179529351ee19bc4ca181f.gif' style='vertical-align: middle; border: none; ' class='tex' alt=$ {\frac{d(2x+d)+R^{2}}{d(2x+d)}})-(x+d) R^{2}=0" />

$d(2x+d)<span class='MathJax_Preview'><img src='http://www.infinitoteatrodelcosmo.it/wp-content/plugins/latex/cache/tex_e23935a0b30019d9a9b0a2c48f4f9a7b.gif' style='vertical-align: middle; border: none; ' class='tex' alt=$ {d(2x+d)+R^{2}})-(x+d) R^{2}=0" />

${d(2x+d)^{2}+(2x+d)R^{2}}-(x+d) R^{2}=0$

${d(4x^{2}+d^{2}+4xd)+(2x+d)R^{2}}-(x+d) R^{2}=0$

$4dx^{2}+d^{3}+4xd^{2}+2xR^{2}+dR^{2}-xR^{2}-R^{2}d =0$

che porta all'equazione di 2° grado:

$4dx^{2}+(R^{2}+4d^{2})x+d^{3}=0$

Calcoliamo prima il discriminante:

$\Delta =R^{4}+16d^{4}+8R^{2}d^{2}-16d^{4}=R^{4}+8R^{2}d^{2}=R^{2}(R^{2}+8d^{2})$

poi le come radici:

$x_{1,2}=\frac{-(R^{2}+4d^{2})\pm R\sqrt{R^{2}+8d^{2}}}{8d}$

osserviamo che per c=0, la derivata non si annulla, quindi $a(0)=\sqrt{d^{2}+R^{2}}$ non è il minimo cercato.

La prima radice , è:

$\frac{-R^{2}-4d^{2}- R\sqrt{R^{2}+8d^{2}}}{8d}<-\frac{d}{2}$ proviamo a vedere

$-R^{2}-4d^{2}- R \cdot \sqrt{R^{2}+8d^{2}}<-4d^{2}$

$R^{2}+4d^{2}+ R \cdot \sqrt{R^{2}+8d^{2}}>4d^{2}$ che è vero, quindi la scartiamo

consideriamo la seconda soluzione e vediamo se

$\frac{-R^{2}-4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d}>-\frac{d}{2}$

$-R^{2}-4d^{2}+ R \cdot \sqrt{R^{2}+8d^{2}}>-4d^{2}$

$R \cdot \sqrt{R^{2}+8d^{2}}>R^{2}$ che è vero . Quindi questa è la soluzione da prendere, ed è un minimo per la funzione a(x)

$a(x)=(x+d)\cdot \sqrt{1+\frac{ R^{2}}{d(2x+d)}}$

calcoliamo (x2+d), (2x2+d)

$x_{2}+d=\frac{-R^{2}-4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} +d=\frac{-R^{2}+4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d}$

$2x_{2}+d=2\frac{-R^{2}-4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} +d=\frac{-R^{2}+ R\sqrt{R^{2}+8d^{2}}}{4d}$ $a(x_{2})=\frac{-R^{2}+4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} \sqrt{1+\frac{R^{2}}{2d\frac{-R^{2}+ R\sqrt{R^{2}+8d^{2}}}{4d} }}$

$a(x_{2})=\frac{-R^{2}+4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} \sqrt{1+\frac{R^{2}}{\frac{-R^{2}+ R\sqrt{R^{2}+8d^{2}}}{2} }}$

$a(x_{2})=\frac{-R^{2}+4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} \sqrt{1+\frac{2R^{2}}{\frac{-R^{2}+ R\sqrt{R^{2}+8d^{2}}}{1} }}$

$a(x_{2})=\frac{-R^{2}+4d^{2}+ R\sqrt{R^{2}+8d^{2}}}{8d} \sqrt{\frac{R^{2}+R\sqrt[]{R^{2}+8d^{2}}}{-R^{2}+\sqrt{R^{2}+8d^{2}}}}$
Vincenzo Zappalà

10/11/2016 at 18:58

perfetto! Scrivete tutto per bene in un articolo e lo pubblichiamo a vostro nome... o -per semplificare- lo inserisco io, dicendo subito che è vostra opera!!!

Come preferite...

Grazie e complimenti!!!! Un gran bell'esercizio, utile per tutti.

Ho notato che alcune cose si leggono male ... è meglio scriverlo proprio come articolo, spiegando bene tutti i passaggi...
Umberto

10/11/2016 at 20:28

hai ragione, alcune formule latex non vengono interpretate, bisognerà chiedere a SMA

questo nei commenti, nell'articolo di prova che ho scritto si vede tutto correttamente,

e ci sono tutti i passaggi

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

Soluzione definitiva (?) del satellite attorno a Papalterra ***

Articoli correlati

Un problema di ... conservazione ***

I tassisti delle foglie *

Perché il problema dei tre corpi è caotico ? **

Galileo e Newton: due linguaggi diversi o soltanto un'infarinatura di astrodinamica? **

37 commenti

Lascia un commento Cancel Reply