Il quiz sul triangolo (QUI) si risolve immediatamente ricordando un teorema molto antico. Non lo dico nella presentazione per non influenzare chi cerca ancora di risolverlo in qualche altro modo. Va comunque detto che i nostri maghi sono stati più che bravi… Aggiungiamo qualche considerazione su come questo esercizio permetta di trovare graficamente ed elegantemente una formula fondamentale della trigonometria e su come le tabelle trigonometriche, largamente in uso prima dell’avvento dei computer moderni, si poggino su questa relazione.

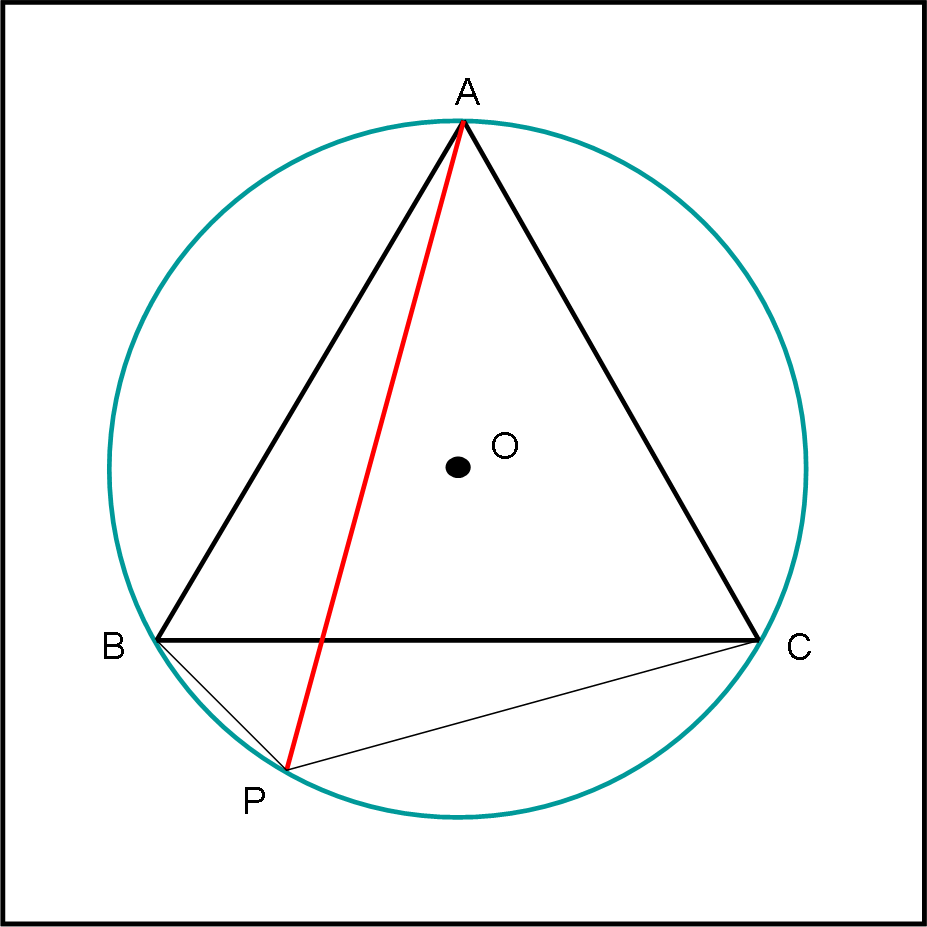
Riprendiamo la nostra figura e completiamola con i due segmenti BP e PC. Cosa otteniamo? Un quadrilatero inscritto in una circonferenza. Bene… basta chiedere a Tolomeo e farsi enunciare il suo teorema che dice: “Per ogni quadrilatero inscritto in una circonferenza la somma dei prodotti delle misure dei lati opposti è uguale al prodotto della misura delle due diagonali”.

Il quiz è praticamente risolto applicando, al nostro caso l’enunciato:

AB ∙ PC + AC ∙ BP = AP ∙ BC

Sapendo che AB = AC = BC (per costruzione), basta dividere l’espressione precedente per questa lunghezza e si trova:

PC + BP = AP

CVD

Ma il teorema istiga un nuovo quiz...

QUIZ: la soluzione è immediata se si conosce il teorema. Può essere, invece, interessante dimostrare il teorema. Ma se ne è stato capace Tolomeo, ne sarete capaci anche voi…

Il teorema di Tolomeo è utilissimo per trovare una delle formule fondamentali della trigonometria (quella di sottrazione del seno), che abbiamo già usato varie volte (e anche ricavato QUI), ossia quella che dice:

sen (α - β) = sen α  cos β  - cos α sen β

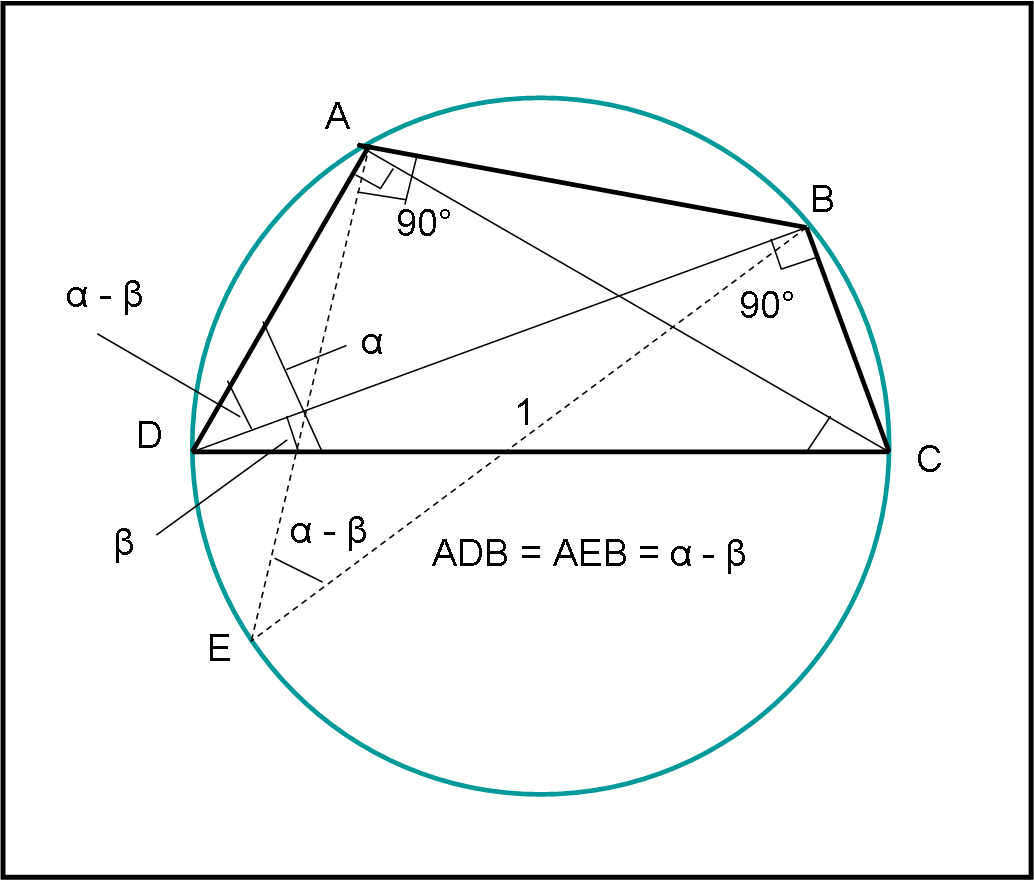
Costruiamo nella figura che segue un quadrilatero particolare, ossia che abbia un lato uguale al diametro della circonferenza, posto uguale all’unità (CD = 1).

Gli angoli in DAC e DBC sono retti, dato che iscritti su mezza circonferenza. Segue dai triangoli DAC e DBC che:

DC sen α = 1 · sen α = AC

sen β = BC

cos α = AD

cos β = BD

Ricordando che gli angoli alla circonferenza relativi a uno stesso arco sono uguali, tracciamo da A la perpendicolare al lato AB che incontra la circonferenza in E. Possiamo scrivere:

ADB = AEB = α – β

Dal triangolo rettangolo (per costruzione) EAB  si ha:

AB = EB sen (α – β) =  sen (α – β)

Scriviamo il teorema di Tolomeo per il quadrilatero ABCD:

AB ∙ DC + AD ∙ BC = AC ∙ BD

sen (α – β) ∙ 1 + cos α sen β = sen α cos β

sen (α – β) = sen α cos β - cos α sen β

CVD

Abbiamo, infatti, dimostrato la formula della sottrazione del seno, attraverso un procedimento molto elegante, tipico dei grandi scienziati greci.

Conoscendo i valori del seno e coseno per angoli “particolari”, è, così, possibile trovare il seno di angoli sempre più piccoli e costruire le tanto utili tavole trigonometriche.

Ricordiamo ancora che le tabelle sono state in uso fino all’avvento delle calcolatrici elettroniche e sono state proprio loro (vista la grande importanza che rivestivano in moltissimi campi) a stimolare l’invenzione dei primi sistemi automatici di calcolo.

A volte, basta un triangolo equilatero per scoprire moltissime applicazioni, oltre che scatenare la grande preparazione dei nostri maghi!

Le loro brillanti soluzioni, oltre che il quiz, le trovate QUI