Intanto grazie a tutti i partecipanti; la soluzione di Leandro grosso modo va bene; grazie anche a Oreste per aver messo in luce l'aspetto grafico del problema. La soluzione generale è comunque algebrica. Il testo completo del quiz lo trovate QUI.

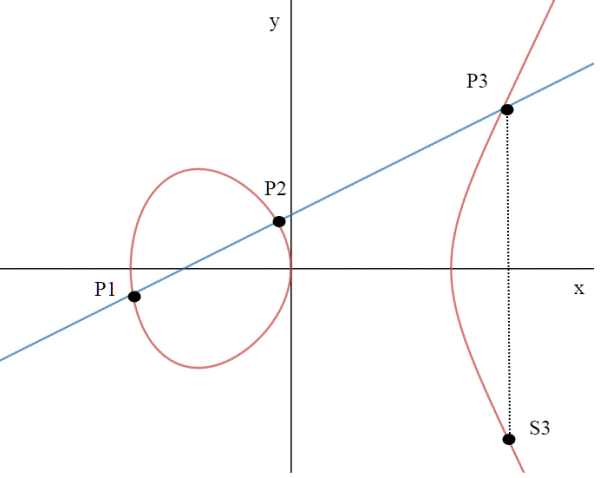
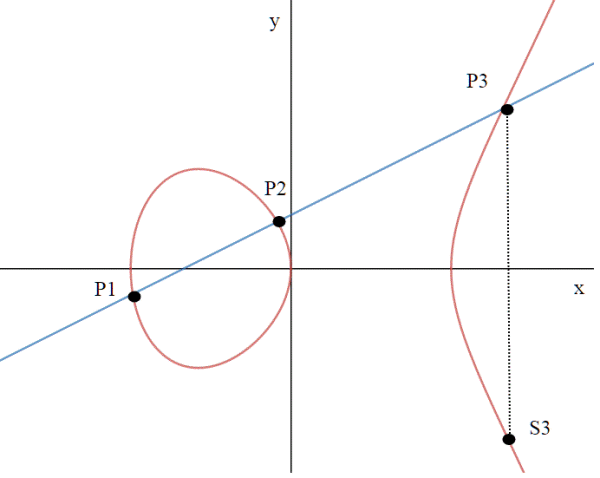
Ricordo  che il testo del quiz richiedeva, noti P1 e P2, di trovare S3, punto simmetrico rispetto all'asse delle x della terza intersezione P3 con la curva di equazione .

Faccio i conti in generale, usando l'equazione ; questo perchè la curva del quiz è un caso particolare di una curva detta ellittica che  è sempre riconducibile ad una espressione di tale tipo, nota anche come equazione di Weierstrass.

Osserviamo innanzitutto che se esiste P3 allora esiste anche S3; questo deriva dal fatto che se (x₃,y₃) è una soluzione dell' equazione  allora anche (x₃,-y₃)  è una soluzione, essendo 

per quanto riguarda l'ellittica uso tale equazione; per la retta calcolo prima il coefficiente angolare

(nel testo del quiz abbiamo supposto )cIn tal modo l’equazione della retta diventa

y = m(x−x₁)+y₁  (retta passante per x₁,y₁ e coefficiente angolare noto)

Per determinare le  intersezioni, quindi, bisogna fare il sistema fra retta ed ellittica; ci basta sostituire a y la sua espressione sulla retta:

il primo membro risulta:

a noi interessano solo i termini in  , le costanti le conglobiamo in un unica costante c:

e qui interviene il nostro "uovo di Colombo": conosciamo già due radici di questo polinomio di terzo grado, e sono ancora x₁,x₂; quindi esiste anche la terza soluzione e possiamo scomplorlo  in fattori.

Infatti abbiamo un polinomio di terzo grado; essendo x₁ una radice è divisibile per (x-x₁)

quindi il polinomio può essere scomposto nel prodotto di un termine di primo grado con uno di secondo grado. Ma le radici sono due e sono distinte, quindi anche quello di secondo grado è scomponibile nel prodotto di due termini di primo grado.

Se t è la terza radice:

=

a noi interessano i termini in :

Confrontando questa espressione con  vediamo che il coefficiente del termine di secondo grado deve essere:

quindi 

ma t=x₃, se sostituiamo nella retta y = m(x−x₁)+y₁. otteniamo:

Per trovare adesso il punto speculare S3 a P3, basta cambiare di segno y₃:

       Xs3 resta invece la stessa, ovvero X3

Per ottenere il risultato finale in funzione di x₁, x₂, y₁, y₂ basta sostituire a m il suo valore.

Notiamo una cosa: il risultato finale non dipende direttamente dai coefficienti dell' equazione ossia a,b , ma solo dai due punti -soluzioni. Però questi chiaramente dipendono dall'equazione.

Il quiz è stato introdotto  per parlare di un fatto più generale, riguardante le curve ellittiche; vedremo in altri articoli che le soluzioni di un equazione ellittica formano un gruppo qualora si prenda come operazione fra le coppie (x1,y1) , (x2,y2) proprio la soluzione di qui sopra. Fino ad ora abbiamo dimostrato che è una operazione interna, e si vede subito che è commutativa (posso infatti comodamente scambiare fra di loro i due punti P1,P2 ; la retta per quei due punti sarà sempre la stessa). Ci mancherà di trovare l'elemento neutro e definire l'operazione per x1=x2, ossia nel caso che la retta sia tangente alla curva.

QUI trovate tutti i quiz del Club dei Maghi