QUIZ: Il fantasma di Galois. ***/****
Vi proponiamo un quiz un po' diverso dai soliti, ma che comunque può essere risolto tranquillamente con poche nozioni di geometria analitica e di algebra elementare. E' però molto importante perchè ci introdurrà nel mondo affascinante e misterioso delle curve ellittiche...
Quando Wiles (il matematico che ha dimostrato il teorema di Fermat, di cui abbiamo parlato QUI) si accingeva a trovare un legame fra le curve ellittiche e la congettura di Fermat, sembra proprio che gli sia apparso il fantasma di Galois.
Galois fu forse il più geniale matematico mai esistito, se dobbiamo considerare il fatto che è morto in un duello a soli 21 anni; se fosse vissuto fino all'età di Gauss cosa avrebbe potuto creare? Ma torniamo a noi. Wiles voleva trovare tutte le soluzioni di una certa equazione cubica . Questo più in generale lo aveva già previsto Galois; egli sostanzialmente trattò le soluzioni di una equazione come un gruppo algebrico (i gruppi sono nati proprio così) in cui definire una operazione interna; componendo in tal modo due elementi, che quindi sono due soluzioni, si trova sempre un'altra soluzione (chi ha seguito gli articoli sui gruppi, sa che possiamo, nel caso fortunato , trovare dei generatori per tale gruppo e quindi rappresentare tutte le soluzioni). Come inizio Wiles fece con le curve ellittiche qualcosa molto simile a quello che proporremo come quiz. e questo ci potrà far sentire molto orgogliosi.
Una equazione ellittica è una equazione del tipo (ne consideriamo una in particolar modo, per semplificare il problema):
Questa equazione determina un certo luogo geometrico dei punti del piano, proprio le soluzioni (x,y) dell'equazione, che sono punti del piano o coppie di numeri reali, come preferite .
Disegnare un tale luogo geometrico non è una delle cose più semplici; ma ci si può anche affidare a software di calcolo numerico come questo, non c'è niente di male né da vergognarsi. Ma non è questo il quesito che intendiamo proporvi, che è ben più profondo nelle sue conseguenze.
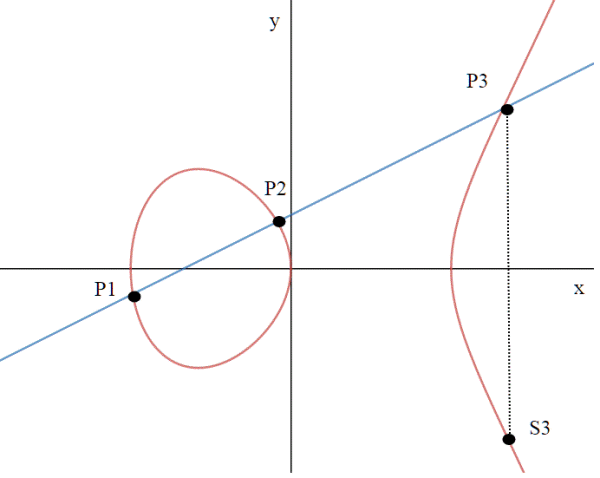
Consideriamo una retta che passi attraverso due qualsiasi punti soluzione dell'equazione ; i punti P1(x1,y1) , P2(x2,y2). Si richiede anche che x1<>x2.
Le domande del quiz sono le seguenti:
- esiste sempre un terzo punto, ulteriore intersezione della retta con la "curva" ellittica?
- Riusciamo a trovare le coordinate del terzo punto P3 in funzione di x1,y1,x2,y2? Il quiz non è facilissimo pur essendo, dal punto di vista degli strumenti di calcolo, un esercizio di geometria analitica delle scuole superiori; c'è però"un uovo di Colombo" che ne permette una semplice impostazione.
- Interessa alla fine trovare anche le coordinate del punto S3, simmetrico di P3, in funzione di x1,y1,x2,y2
(questo problema è chiaramente noto, anche se non è facile reperire la soluzione in rete; so che però a noi non piace "vincere facile" come spesso dice Vincenzo in questi casi.)
QUI la soluzione del QUIZ
QUI trovate tutti i quiz del Club dei Maghi
13 commenti
Se qualcuno trova delle difficoltà nel capire il testo del quiz lo dica pure; non siamo infallibili! Il fatto che il quiz sia stato impostato in modo un po' "mistica" potrebbe far pensare che sia difficilmente risolvibile ma in realtà..non è così.Un piccolo suggerimento; per trovare la terza intersezione della retta con la curva ellittica si tratta prima di trovare l'equazione della retta passante per due punti (che sono noti, sono dei parametri) e poi fare l'intersezione con l'equazione ellittica.. ma fare l'intersezione (se ricordate per esempio l'intersezione retta-circonferenza) vuol dire risolvere un sistema.. Pautasso prova anche tu e facci sapere!
Prendiamo la retta
ove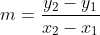
e 
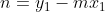
l'intersezione della retta e della ellittica risulta dalla equazione:
sviluppando si ha l'eq di terzo grado
ma per le formule di Viete le 3 soluzioni hanno somma
da cui
e anche
poiché le ipotesi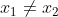
implicano m ed n finiti
possiamo sempre trovare la terza intersezione finita.
Suppongo sia immediato trovare il punto s3 simmetrico
molto molto interessante..ma forse non tutti sanno cosa sono le formule di Viete; potresti..
più semplicemente un'equazione algebrica può essere sempre espressa nella forma
perchè se x vale una qualsiasi radice, il prodotto è nullo.
Sviluppando si ottiene
quindi il coefficiente del termine di grado 2 è uguale alla somma delle radici, cambiata di segno
Bisognerebbe esprimere le coordinate di S3 (x3,y3) in funzione di x1,y1,x2, y2, ovvero eseguire le dovute sostituzioni. Comunque.. siete tutti d'accordo sulla soluzione di Leandro?
Buonasera a Maghi e Lettori.
Dopo una giornata di accanite fotocopie al CAC ho finalmente il tempo di ammirare questa soluzione pulita pulita del Signor Leandro. Sissignori mi pare proprio che sia la giusta risposta al quesito.
A questo punto non c'è molto da aggiungere. Però vorrei far presente una cosa, che a volte può capitare, se uno si lascia suggestionare dalla figura e non approfondisce con calma lo studio della funzione.
Per esempio il grafico di questa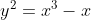
....
A vederlo così, uno potrebbe pensare che, inclinando un po' di più in verticale la linea azzurra, ad un certo punto l'intersezione con P3 non si può più avere..... Sbagliato !!
Sembra che sia così, perché il ramo di destra che "assomiglia" ad un ramo di iperbole, dà la sensazione di una curvatura sempre decrescente per valori crescenti di x. Magari uno può pensare che ci sia anche il suo bell'asintoto ma niente di più.
Ma se ingrandiamo un po il campo di visualizzazione la curva ha il seguente aspetto...
Vedete che la retta che taglia in due punti il lobo di sinistra, con una pendenza piuttosto verticale, sembra divergere dal ramo di curva a destra e non essere destinata ad incontrarle nel fatidico punto P3. Invece...
Guardando meglio si può notare che, ad un certo punto, la curvatura di questa linea cambia.
Come si fa a capire se è vero? lo si capisce dal segno della derivata seconda: sè è positivo la linea è concava, se è negativo è convessa.
Allora, se pongo a zero questa derivata seconda, posso trovare per quale valore di x la linea si flette cambiando il segno della curvatura.
Come dico sempre a mio nipote Oreste: adesso facciamo un esempio.
La funzione è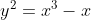
la riscrivo così...})
Considerando i valori di y positivo (la parte della curva sopra l'asse x), calcoliamo....
la sua derivata prima y'=/2\sqrt{(x(x^2-1)})
la sua derivata seconda y" =/4\sqrt{(x(x^2-1))^3})
poi vediamo per quale x il numeratore vale zero...
= 0
e adesso... giù a trovare le radici di questa equazione biquadratica, che sono x =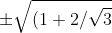
= 1,467 circa.
In effetti, in corrispondenza a x = 1,467 con})
= 1,3 ( e -1,3) , si nota nel grafico un leggero cambiamento della curvatura (osservare a sinistra e a destra della linea verticale blu). Questo cambiamento porterà la retta rossa ad intersecare ad un certo punto la linea della funzione nel punto P3.
Tutto questo ragionamento, ovviamente, non serve se si segue la strada indicata dal Mago e percorsa da Leandro, un modo di arrivare subito , precisi, alla soluzione. Ma siccome a volte, come dicono a Cuneo, "l'apparenza inganna" ricordiamoci sempre che il grafico, da solo, non basta a capire che razza di sarchiapone stiamo analizzando.
Doverosi ossequi
Oreste Pautasso
ottimo Oreste; hai centrato un problema grafico-visivo molto importante, che non sempre viene messo in luce in questo contesto.
Complimenti a Leandro per la soluzione.
Vorrei chiedere a Leandro una conferma/chiarimento sul suo secondo post. La sviluppo del prodotto (x-x1)(x-x2)(x-x3) non porta direttamente alla espressione che indichi. C'è qualche passaggio ulteriore che mi sfugge?
Comunque anche nello sviluppo diretto i primi due termini sono quelli. Quindi, non cambia nulla ai fini della risposta del quiz.
Ho anche una domanda per Oreste Pautasso.
Il fatto che i due rami di questa curva per x>1 abbiano un flesso è necessario affinchè possano intersecare la retta, qualsiasi sia la sua pendenza. Ma è anche sufficiente? La derivata prima, dopo essere diventata positiva, potrebbe anche tendere ad un limite finito. In questo caso comunque tende ad infinito e quindi "taglierà la strada" alla retta, qualsiasi sia m.
Il quiz è ancora aperto; la soluzione di Leandro è molto elegante, ma andrebbe esplicitata di più.
Per quanto riguarda lo studio grafico, consideriamo molto interessante l'intervento di Oreste a titolo di completamento grafico-visivo, ma non è per noi necessario. Questo per il semplice motivo che non tutti conoscono il calcolo differenziale, e non vorremmo escludere alcun lettore da discussioni troppo specialistiche.
Grazie a Fabrizio per la domanda ( e la risposta) che è proprio coerente con l'idea di usare il disegno come ispiratore di domande. In questo caso il limite della derivata prima per x infinito vale infinito in modo evidente, in altri casi andrebbe proprio calcolato perché il suo valore ci dice con quale pendenza la linea si assesta.
Aggiungo solo una piccola precisazione. Nel testo del tuo post scrivi:
"La derivata prima, dopo essere diventata positiva, potrebbe anche tendere ad un limite finito."
Ma la derivata prima (mi riferisco come già detto al ramo superiore della funzione) è sempre positiva, ciò che varia è la sua tendenza, prima a decrescere fino al punto di flesso, e poi a crescere, successivamente.
La variazione di segno, prima e dopo il flesso riguarda la derivata seconda.
Quindi, per non lasciare eventuali dubbi riscriverei la frase in questo modo....
"La derivata prima (superato il punto in cui la derivata seconda diviene positiva), potrebbe anche tendere ad un limite finito."
Che penso fosse precisamente ciò che intendevi.
Giusto Oreste. Scusa per l'errore nella formulazione della domanda.
La mia incapacità digitativa nell'uso del function editor mi ha fatto scrivere un cavolata.
L'espressione della eq di terzo grado corretta è
Non me ne voglia Galois che proprio da queste simmetrie nei coefficienti derivò la teoria dei gruppi, infatti il primo consiste nella somma dei coeff presi uno per volta, il secondo è la somma dei coeff presi a due a due e il terzo presi a tre a tre.
L'espressione della eq di terzo grado corretta è
scusate, i segni sono sempre alterni (+,-,+,-)
Per inciso sulla questione dei disegni , se osserviamo i disegni fatti da Archimede nel suo Metodo ci rendiamo conto che sono totalmente sballati. Questo non è una imprecisione. Il Grande voleva solo non ingannarci con le somiglianze dette "a vista".