Categorie: Matematica Teoria degli insiemi
Tags: Club dei Maghi quiz
Scritto da: Club dei Maghi
Commenti:7
Soluzione del quiz "Pitagora ad n-dimensioni"
Come tutti avranno capito , la parte iniziale del quiz che trovate QUI non ha soluzione, ovvero per n>2 non è possibile trovare degli interi a,b,c tali che:
per n>2
e che altro non costituisce che l'ultimo teorema di Fermat, Useremo la sigla UTF per indicare tale teorema; in realtà sarebbe più corretto chiamarlo teorema di Wiles, in quanto fino alla sua dimostrazione l'UTF era una congettura.
Il perchè della seconda parte del quiz
Trovare le soluzioni intere dell'equazione
dà un esempio di come procedere per risolvere problemi legati alla soluzione di equazioni che rappresentano delle curve piane, interessandoci di più alle soluzioni intere o razionali. E' più o meno quello che hanno fatto i matematici che hanno contribuito alla soluzione del Teorema di Fermat. Su questo "più o meno" potremmo discuterne per anni. Inoltre l'espressione che troveremo per le terne è stata usata proprio da Fermat per la soluzione del caso n=4.
Soluzione della seconda parte del quiz.
La seconda parte del quiz richiedeva quindi un metodo per trovare tutte le soluzioni intere dell'equazione: nel caso n=2, ovvero tutte le terne pitagoriche, ovvero le terne a,b,c per cui:
Stiamo affrontando un problema che si può generalizzare; lo studio delle equazioni diofantee. Un'equazione diofantea è un'equazione in una o più incognite con coefficienti interi di cui si ricercano le soluzioni intere.
Spesso quando si affrontano problemi di questo tipo, in cui si cercano soluzioni intere, è meglio rifarsi a cercare delle soluzioni razionali, che poi possono essere facilmente trasformate in soluzioni intere. Secondariamente, l'appoggio a una figura geometrica, in particolare modo a una curva,riesce a inquadrare meglio il problema.
Se dividiamo ambo i membri dell'equazione:
per
otteniamo l'equazione:
; ponendo x=a/c, y=b/c possiamo ridurci a studiare le soluzioni razionali dell'equazione:
che è l'equazione di una circonferenza con centro nell'origine; ripeto , di questa circonferenza cerchiamo i punti con coordinata razionale.
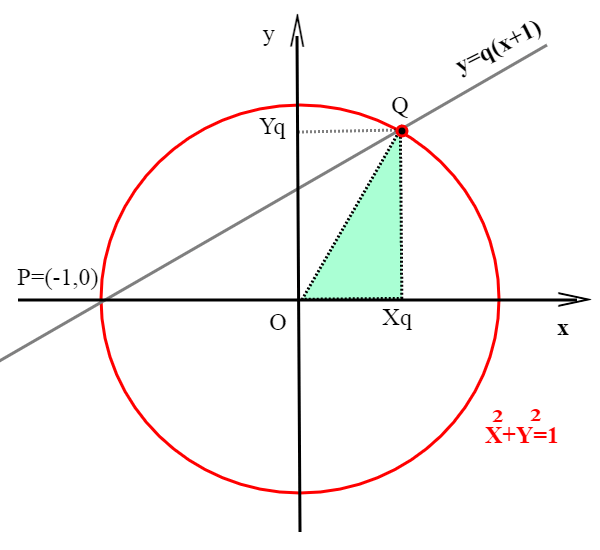
per far ciò, consideriamo la retta y=(q+1)x passante per il punto P(-1,0) che è anche un punto della circonferenza . Al variare di q 1 a 0 esclusi otteniamo tutti i triangoli rettangoli (azzurrini) OXqQ possibili; Ma veniamo ai calcoli; sostituiamo nell'equazione della circonferenza ,l'espressione di y sulla retta;
otteniamo:
; questo è un polinomio in x, q è un parametro ; essendo x=-1 una soluzione, tale polinomio deve essere divisibile per (x+1); applicando la regola di Ruffini dividiamo tale polinomio per (x+1) ottenendo:
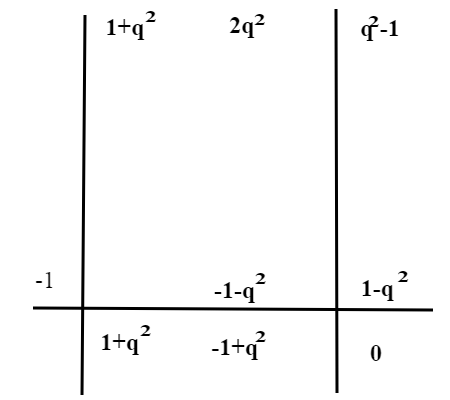
per cui, a parte x=-1, le altre soluzioni sono da cercare con:
ovvero:
x è razionale se q è razionale; infatti si ottiene con somme, prodotti e frazioni di un numero razionale.
ricaviamo allora l'espressione di y direttamente dall'equazione della retta:
y=q(x+1); sappiamo già che essendo sia x che q razionali anche y sarà razionale.
notiamo che:
2) come deve essere.
quindi per ottenere tutte le soluzioni razionali per (x,y) basta sostituire a q un qualsiasi numero razionale. Ricordiamoci adesso che x=a/c, y=b/c e facciamo un esempio numerico; poniamo q=1/2. Allora:
;
; quindi a=3, b=4, c=5
Facciamo un altro passo ed esprimiamo q come rapporto fra due interi m,n; facendo variare m, n otteniamo tutti valori possibili di q. Poniamo quindi q=m/n
Essendo possiamo limitarci a prendere gli interi m, con 0< m<n
Da qui,o dal fatto che q è razionale, vediamo anche che le soluzioni sono un'infinità numerabile.
ponendo
quindi
quindi
Un'ultima osservazione; le terne in cui a,b,c sono primi fra loro sono dette primitive, mentre le altre derivate. Lascio a voi dire che relazione debba esserci fra m,n per ottenere terne primitive.
Un po' di storia e i tentativi di soluzione della congettura di Fermat
Ho cercato di ricostruire brevemente la storia della soluzione cercando varie notizie e aneddoti.
Riprendiamo l'enunciato della congettura:
non ha soluzioni intere per n>2
Come nel quiz iniziale, Fermat voleva estendere ad esponenti maggiori di 2 la ricerca di terne "pitagoriche".Fermat di dilettava nel leggere i problemi proposti nel Libro II dell’Arithmetica di Diofanto, (Grecia, circa 250 d.C.)
Fermat affermava di possedere la soluzione nel caso generale,ma non poteva trascriverla sul bordo troppo misero della pagina.. circa tre secoli dopo un brillante matematico Inglese, Andrew Wiles, dopo anni di studi in segreto, scrisse la soluzione generale, che occupò più di 100 pagine.
Fermat stesso scrisse la dimostrazione per gli esponenti n=3 e n=4, utilizzando un metodo da lui inventato, detto della discesa infinita, che è un particolare tipo di dimostrazione per assurdo, che può apparire a prima vista un po' strano.
La discesa infinita afferma:
Non esiste una proprietà che, se soddisfatta da un intero positivo, possa essere soddisfatta da un intero positivo più piccolo.
Il metodo della discesa infinita dimostra che alcune proprietà o relazioni sono impossibili, se applicate a numeri interi positivi, infatti, se si prova che queste
valgono per qualsiasi numero, queste devono valere anche se si considerano numeri
più piccoli; ma questi ultimi, a loro volta, per le stesse motivazioni precedenti, devo
valere per alcuni numeri ancora più piccoli, così fino all’infinito. Questo processo è
impossibile, in quanto una sequenza di numeri interi non può decrescere all’infinito.
Nel 1729 il grande matematico tedesco Eulero che allora aveva 22 anni, venne a conoscenza delle famose annotazioni di Fermat, ed iniziò ad occuparsi della congettura, di cui diede una dimostrazione nel caso n=3.Negli altri casi non approdò a nulla e arrivò persino a chiedere ad un suo amico di frugare nella casa di Fermat alla ricerca di eventuali foglietti abbandonati.
Nel 1816 l’Accademia di Francia mise in palio un premio destinato al primo che avesse dimostrato l’UTF.
Gauss fu invitato alla risoluzione del problema, ma ecco cosa rispose:
“Le sono molto obbligato per la notizia del premio di Parigi, ma confesso che il Teorema di Fermat, come proposizione isolata, presenta scarsissimo interesse per me, perché potrei facilmente enunciare un gran numero di simili proposizioni, che non potremmo né dimostrare né confutare.”
(aggiungo che per fortuna Gauss non se ne occupo', altrimenti non sarebbe probabilmente esistita la geometria intrinseca e l'apparato matematico della relatività Generale).
Nel 1830 Dirichlet risolse i casi n=5 e n=14, tra il 1839 ed il 1840 Lamé e Lebesgue risolsero il caso n=7. Il caso n=5 fu anche risolto da Legendre.
Seguirono le ricerche di Kummer che, intorno alla metà dell’Ottocento, provò l’UTF per un’infinità di esponenti, in particolare per tutti i multipli dei numeri da 3 a 99.
Il risultato di Kummer fu solo il primo di una serie di teoremi di carattere generale che permisero di restringere sempre più il campo di ricerca delle eventuali soluzioni dell’equazione .
Nel 1983 un matematico tedesco di 27 anni,Faltings, provò la congettura di Mordell: da questa segue che per ogni valore di n la ammette al più un numero finito di soluzioni razionali, visti sempre come punti di una curva. Questo fu l’ultimo, e forse il più importante risultato ottenuto prima della completa risoluzione del problema.
Le curve ellittiche
Le curve ellittiche svolgono un ruolo importante nella soluzione dell' UTF; ma cosa rappresentano? Intanto il termine può ingannare, non sono ellissi e quindi coniche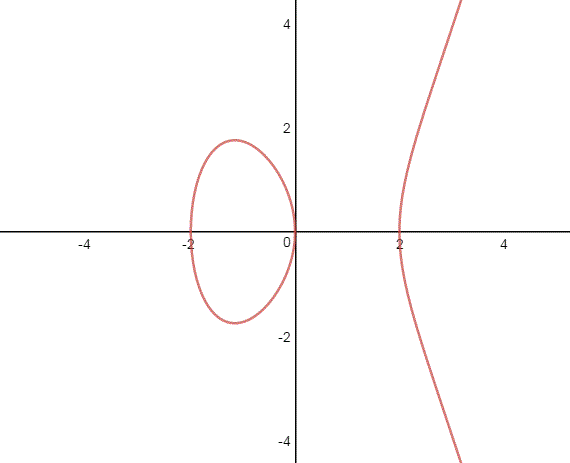 ,ma cubiche. Il nome deriva dalla lunghezza degli archi dell'ellisse, e dallo studio delle distanze percorse dai pianeti.
,ma cubiche. Il nome deriva dalla lunghezza degli archi dell'ellisse, e dallo studio delle distanze percorse dai pianeti.
Esse sono curve del tipo:
y2 = x3 + ax + b
nella figura vedete il grafico della curva di esempio ; le curve ellittiche sono fortemente legate alle soluzioni di certe equazioni riguardanti dei problemi numerici (equazioni diofantee), ed usate anche nella moderna crittografia. Spesso si cercano solo i punti razionali di tali curve, oppure addirittura dei valori finiti tramite l'aritmetica modulare.
La soluzione di Wiles
"La dimostrazione utilizza strumenti di matematica avanzata, e purtroppo non può essere riassunta in termini elementari. Il lavoro di Wiles non è che il coronamento di un progetto di ricerca al quale hanno contribuito, nel corso degli ultimi decenni, matematici di diversa provenienza geografica. L’oggetto fondamentale è dato proprio dalle curve ellittiche. L'idea che spinse i ricercatori in questa direzione è dovuta ai matematici giapponesi Taniyama e Shimura: una congettura da loro formulata tra gli anni 50 e 60 risultò essere strettamente legata all’UTF: il matematico tedesco Frey intuì questa relazione all’inizio degli anni 80, ed il francese Ribet la confermò nel 1986. Wiles pervenne alla dimostrazione dell’UTF proprio passando attraverso la congettura di Shimura-Taniyama."
Impossibile dire di più sulla soluzione di Wiles senza essere a conoscenza delle matematiche pure; già alcune di queste che sto scrivendo nel blog possono costituire il punto di partenza per capire con che strumenti sia stato dimostrato il teorema.Le curve ellittiche hanno infatti anche una struttura gruppale, e possono essere definite su oggetti simili agli interi modulo n. Mi riprometto di aggiungere altri articoli che ci permetteranno fra le altre cose anche la comprensione dell' UTF almeno a grandi linee, ma la strada sarà lunga. Vi ricordo che le matematiche pure non sono più difficili di tanti argomenti trattati in questo sito; sono solo sconosciute. E ci si accorge solo in questi frangenti (dimostrazione dell'UTF) a cosa possono servire. Poi si rimettono nel cassetto.






7 commenti
bellissimo! mi compiaccio anche se non dovrei farlo, ma quando ci vuole ci vuole!!
aggiungo...
questo Circolo sta diventando un vero pozzo di San Patrizio... o meglio "senza fondo"
Dimostrazione molto convincente e apparentemente "facile". Chissà perché tutte le cose che non ci vengono in mente, quando le vediamo risolte, sembrano facili...mah.
Davvero interessante e stimolante la storia della congettura di Fermat e la descrizione sintetica della strada percorsa da Wiles, a cui , meno di un anno fa, è stato conferito anche il prestigioso premio Abel proprio per la sua dimostrazione e per l'uso che è riuscito a fare delle intuizioni proprie e altrui.
Certo, la complessità non si supera solo con la forza bruta dei supercomputer, che pure serve, ma anche con la fantasia e la capacità di riuscire a "mettere insieme" i frammenti di un puzzle che sono sparsi nel mondo delle idee e che magari resterebbero isolati, per decenni o secoli, se qualcuno non fosse in grado di comprenderne l'utilità.
Quanto alla relazione che deve esistere tra i parametri m ed n , (che generano a,b,c) affinché a,b,c siano primi tra loro come richiesto vorrei fare le seguenti considerazioni:
1 . essendo a= n*n - m*m intero >0 dovrà essere n>m e questa è già una condizione.
2. abbiamo ancora b= 2*m*n e c=n*n + m*m da prendere in considerazione...
Si vede subito che se n e m sono entrambi pari tutti e tre i valori di a,b,c saranno pari, quindi non saranno primi tra loro.
analogamente se n ed m sono dispari, avremo a,b,c pari, come prima.
Dunque perché a,b,c non siano tutti pari basta che m ed n siano uno pari e l'altro dispari, ossia che il prodotto m*n sia dispari.
Ma dire che m ed n non devono essere entrambi pari vuol dire, generalizzando, che non devono avere divisori comuni, ossia che m ed n devono essere primi tra loro (implicando così la precedente condizione).
Quindi, riassumendo m ed n devono essere primi tra loro, con n>m
Questo è ciò che vedo a prima vista, potrebbe essere tutto qui. Però, se sbaglio non buttatemi nel pozzo (di San Patrizio), non sono abituato alla discesa infinita)
E poi, sono curioso di vedere cosa ci riserva Mago Umberto.
Per chi fosse interessato alla dimostrazione di Wiles dell'ultimo teorema di Fermat
consiglio il libro L'ULTIMO TEOREMA DI FERMAT di Sìmon Singh
E' una esposizione divulgativa ma molto ben fatta e avvincente di come
Wiles sia giunto a dimostrare l'ultimo teorema di FERMAT ed è anche un
affascinante percorso nella teoria dei numeri
grazie Maurizio; in fin dei conti il tuo tentativo di dimostrazione è servito anche a me; ho preferito impostare il tutto in modo geometrico con il cerchio unitario come avevi fatto tu, ci sono altre soluzioni meno "visive" e puramente algebriche.
Grazie anche a Fiorenzo per la segnalazione del libro.
Comunque ho deciso di scrivere il primo articolo sulle curve ellittiche dal punto di vista gruppale, per collegare il tutto a Galois e alle soluzioni di equazioni polinomiali usando appunto il concetto di gruppo. Ciò è, in parte, quello che ha fatto Wiles.
Bravissimi, siete proprio dei maghi!