11/01/17

QUIZ: Pitagora a n dimensioni

Categorie: Matematica Tags: Club dei Maghi dimensioni Pitagora Quazel quiz Scritto da: Club dei Maghi Commenti:14

Cari amici terricoli,

se qualcuno pensava di essersi liberato di me, mi dispiace deluderlo ma, più mi guardo in giro, più il vostro pianeta mi piace e ho intenzione di conoscerlo molto bene prima di tornare nel mio! Come qualcuno di voi avrà già capito, sono Quazel l’alieno e, grazie al prezioso aiuto di PapalScherzone che riesce a comprendere e a tradurre il mio linguaggio, sto per proporvi un nuovo quiz!

L’idea mi è venuta leggendo alcuni articoli che sono stati pubblicati di recente in questo blog, grazie ai quali avete imparato a non sottovalutare le capacità dei grandi pensatori greci riguardo ai numeri interi (QUI) e siete addirittura riusciti ad esplorare universi paralleli (QUI), abitati da popolazioni di numeri con caratteristiche del tutto peculiari, la cui importanza si è ingiustamente persa nel tempo. Non siete ancora arrivati ai numeri perfetti… eppure avete già valicato le 3 dimensioni, immergendovi degli Universi a n dimensioni.

Visto che sono abituato a giocare quotidianamente con le dimensioni di qualsiasi ordine, ecco a voi cosa ho pensato…

Tanto per cominciare, non stupitevi se vi dico che conosco perfettamente l’universale teorema di Pitagora che, espresso in termini puramente numerici, ci dice:

a² + b² = c²

Esistono sempre due numeri interi a e b, tali che la somma dei loro quadrati dia come risultato il quadrato di un terzo numero intero c. Un esempio, ben conosciuto da tutti? Il numero 3 e il numero 4. Il quadrato di 4 è 16; quello di 3 è 9. La loro somma è 25, che è il quadrato di 5. Perfetto. Una nuova splendida capacità dei numeri quadrati… (per non complicarvi troppo la vita, nonostante io sia abituato a ragionare in base 8, come avete visto QUI, i numeri che sto scrivendo sono nella “vostra” base 10).

Darne una rappresentazione grafica è molto semplice! Se la somma dei quadrati costruiti sui cateti è uguale al quadrato costruito sull’ipotenusa, basta disegnare un triangolo rettangolo e il gioco è fatto!

Tuttavia, per un tipo strano come me (e per gli stessi terricoli greci), la faccenda, se posta in questi termini, è un po’ troppo limitata. Così come esistono i numeri quadrati, abbiamo visto che esistono quelli cubici, a 4, a 5, a n dimensioni. Come si trasforma il teorema di Pitagora? La soluzione si può descrivere sia graficamente sia numericamente, restando, per semplicità, sempre nel campo dei numeri interi.

Ad esempio si può considerare uno strano triangolo rettangolo a tre dimensioni come quello di Fig. 1

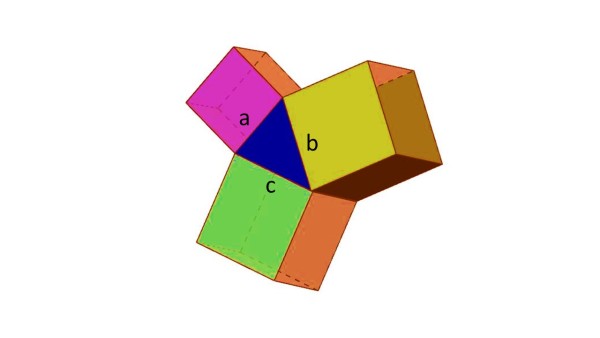
e trovare un “cubo” di un certo lato (collegato ovviamente ad a, b e c o alle facce A , B e C) tale che la somma di questi cubi costruiti sulle facce inclinate (cateti) dia come il risultato un analogo cubo costruito sulla faccia (ipotenusa?) sistemata in orizzontale. E che fare, poi, con figure a 4 dimensioni? Un bel problemino geometrico, così come è un bel problemino matematico riuscire a verificare la relazione equivalente:

a³ + b³ = c³

relativa a una qualche figura geometrica… Limitiamoci alle tre dimensioni e sarà già interessante…

Esistono due cubi costruiti su due delle facce del prisma illustrato in figura tali che la loro somma dia il cubo costruito sulla terza faccia?

Con uno sforzo di immaginazione, passando quindi dal 3D al 4D, al 5D... nD, è possibile trovare due entità n-dimensionali tali che la loro somma dia una entità n-dimensionale ?

Un consiglio di cuore... non fermatevi alle apparenze e pensateci bene prima di dare la vostra risposta, visto che ho intenzione di aspettare almeno una decina di giorni prima di darvi la mia!

Quazel

Un' altra domanda, per ravvivare un po' il quiz; sappiamo che l'equazione:

$a^{n}+b^{n}=c^{n}$

ammette risultati interi nel caso n=2; La domanda è:

Quanti sono questi risultati?
Si possono trovare dei metodi , degli algoritmi,dei procedimenti per esprimere tali risultati? Se si, descrivere tali metodi. Chiaramente bisogna giustificare le risposte.

Chiaramente anche questo problema è già stato ampiamente studiato nel corso dei secoli; non cerchiamo le soluzioni classiche (facilmente reperibili in rete), ma qualsiasi metodo frutto della vostra fantasia e creatività matematica.

QUI trovate tutti i quiz del Club del Maghi

14 commenti

Gimar

11/01/2017 at 13:22

Penso che la figura (1) inganni! Come fa la figura costruita su "b" ad essere un cubo? "c" non è uguale a "b" e non è uguale ad "a".
maurizio

11/01/2017 at 13:29

La domanda mi ricorda un celebre teorema, la cui dimostrazione risale a una ventina di anni fa, rimasto insoluto per tre secoli e mezzo....

Se non si tratta di quel teorema, ma di una diversa questione, limitando il ragionamento alle tre dimensioni, non riesco a collegare le facce del prisma ai tre cubi.

Intendo dire che se, in generale, ogni cubo ha un lato diverso, (es. 3,4,5) il prisma non potrà avere delle facce quadrate (che combaciano con la faccia quadrata del cubo a contatto).

Inoltre lo spigolo di contatto tra due cubi, ad esempio quello di lato b e quello di lato c nella figura, non può avere contemporaneamente lunghezza b e lunghezza c.

Insomma riesco ad immaginare un prisma a base triangolare con una superficie laterale costituita da tre rettangoli della stessa altezza e di basi a, b, c, in generale diverse, e tre parallelepipedi appoggiati a quei rettangoli ma, se uno di essi è un cubo, gli altri due non possono essere cubi.

Il chiarimento che chiedo all'amico Quazel, l'alieno ( che ormai è uno dei nostri) è quindi se devo lasciare da parte le immagini e pensare solo a dimostrare la possibilità o l'impossibilità di trovare valori che soddisfino la formula "pitagorica" su n dimensioni, ( con a, b, c interi positivi ) oppure non ho ben compreso la domanda.
Vincenzo Zappalà

11/01/2017 at 14:40

buon giorno, sono un amico di Quazel (Quizap) e scrivo tramite la gentilezza di Vin-Census, incontrato nel suo viaggio su Andromeda. Per non creare confusione, volevo dire che non è detto che la figura non possa essere qualcosa di più complicato e i "cubi" abbiano spigoli di contatto... diversi... i maghi hanno semplificato un po' il problema geometrico.... ah questi maghi terrestri!!!!

xtqullalà
Gimar

11/01/2017 at 15:34

"...i maghi hanno semplificato un po' il problema geometrico..."

Il triangolo rettangolo è diventato isoscele!

Mi spiace Enzo, ma non capisco la domanda. Fermat aveva già detto che con n> 2 non ci sono soluzioni e di recente l'hanno anche dimostrato, ma sicuramente il quiz vuole qualcosa di diverso|
leandro

11/01/2017 at 16:05

Beh Fermat si era limitato ai numeri naturali. Se estendiamo il teorema ai reali , esso non vale più. Penso che Quazel abbia delle carte che non vuole ancora scoprire.
maurizio

11/01/2017 at 16:25

Grazie Quizap, in effetti il disegno farebbe pensare che debbano valere contemporaneamente due relazioni:

$a^{3} + b^{3}= c^{3 }$ ed anche $a^{2}+b^{2} = c^{2}$ (per come è tracciato il triangolo). Ma non fermiamoci al disegno.

E' chiaro che il triangolo/prisma è una specie di allegoria, da non prendere alla lettera, utile per simboleggiare il legame "pitagorico" sulle 3 dimensioni o, in generale sulle n dimensioni.

Se ho capito bene, quindi, si chiede di dimostrare se esistono o meno tre numeri interi positivi non nulli, ( a,b,c) tali che $a^{3} + b^{3}= c^{3 }$

Questo per n = 3. Poi generalizzare la dimostrazione per qualsiasi valore di n.

Proporrei una visione geometrica del problema tipo "Lego"...

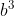Utilizzando $a^{3 }$ mattoncini costruisco un primo cubo. Poi, con $b^{3 }$ mattoncini costruisco un secondo cubo.

smonto i due cubi e vedo se i mattoncini disponibili mi bastano per costruire un cubo che li utilizzi tutti, senza "buchi" e senza rimanenze.

Due esempi non riusciti ...per poco 6, 8, 9 -------> 6*6*6 + 8*8*8 = 9*9*9 - 1 (mi manca un mattoncino)

Ed ancora, 9,10,12 --------> 9*9*9 + 10*10*10 = 12*12*12 +1 (qui, invece, mi avanza un mattoncino)

potrei dire a questo punto che esistono (almeno) 6 numeri (a,b,c,d,e,f) tali che...

$a^{3}+b^{3}+d^{3}+e3=c^{3}+f^{3 }$ ed essi sono rispettivamente a=6, b=8, c=9, d=9, e=10, f=12 E potrei anche aggiungere che, siccome c=d, posso semplificare eliminando i loro cubi e ottenendo:

$a^{3}+b^{3}+e^{3}=f^{3 }$ che assomiglia un po' a Pitagora e, simpaticamente ha un numero di "cateti" pari a 3, come il numero delle dimensioni in gioco.

Così sembrerebbe che un cubo si possa ricostruire come somma di tre cubi, (non di due) almeno in questo caso. Ma questo è decisamente "fuori tema" e mi scuso per la digressione.

Ovviamente la dimostrazione non si può basare su tentativi (anche se, volendo "mostrare" che esiste almeno un risultato valido, basterebbe trovarlo). Volevo semplicemente dare una interpretazione alternativa della raffigurazione spaziale di questo interessante quesito.

Spero di non avere confuso le idee a nessuno e aspetto con curiosità gli sviluppi.
Vincenzo Zappalà

11/01/2017 at 17:24

Guardate che ciò che ha detto Quizap io non l'ho nemmeno letto!!! Non tutti i Quazelliani sono intelligenti e istuiti

Insomma, siete troppo bravi e non vale la pena confondervi!!!
Club dei Maghi

14/01/2017 at 07:00
N.B. E' stata aggiunta una variante al quiz in fondo al testo, e che riporto anche qui:

Un' altra domanda, per ravvivare un po' il quiz; sappiamo che l'equazione:

$a^{n}+b^{n}=c^{n}$

ammette risultati interi nel caso n=2; La domanda è:
1. Quanti sono questi risultati?
2. Si possono trovare dei metodi , degli algoritmi,dei procedimenti per esprimere tali risultati? Se si, descrivere tali metodi. Chiaramente bisogna giustificare le risposte.
Chiaramente anche questo problema è già stato ampiamente studiato nel corso dei secoli; non cerchiamo le soluzioni classiche (facilmente reperibili in rete), ma qualsiasi metodo frutto della vostra fantasia e creatività matematica.
maurizio

14/01/2017 at 09:37

La relazione ,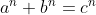 $a^{n}+b^{n}=c^{n}$ nel caso di n=2 corrisponde all'enunciato del teorema di Pitagora.

La rappresentazione grafica, richiamata anche nel testo del quiz di Quazel (scusate la dissonanza...), è quella dei quadrati costruiti sui cateti e sull'ipotenusa di un triangolo rettangolo.

A questo punto chiedersi quanti sono i risultati ammessi equivale a immaginare quanti sono i diversi triangoli rettangoli che si possono disegnare. In altre parole, quante forme può avere il triangolo rettangolo, variando le proporzioni tra i cateti?

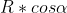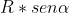
Forse il procedimento più semplice, che mi viene in mente per primo, è di disegnare un cerchio, di far ruotare il raggio "R" di questo cerchio, che assumo sia l'ipotenusa, e di tracciare per ogni posizione i due cateti che altro non sono che $R*cos\alpha$ e $R*sen\alpha$

$(R*cos\alpha )^{2} + (R*sen\alpha )^{2} = R^{2 }$

Naturalmente nel cerchio esiste una simmetria tra i vari quadranti che mi consente di concentrare l'attenzione semplicemente sul primo di essi, per valori dell'angolo $\alpha$ tra 0° e 90°. 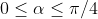Inoltre, se considero l'equivalenza tra triangoli con $\alpha$ compreso tra 0° e 45° ed i triangoli con $\alpha$ da 45° a 90°, dove i valori di seno e coseno si "scambiano", posso dire che i triangoli aventi forme distinte sono proprio quelli che trovo nell'intervallo $0\leq \alpha \leq \pi /4$

Poiché l'angolo, in quell'intervallo, può assumere un numero infinito di valori, direi che altrettanto infiniti sono i triangoli rettangoli e quindi le combinazioni che possono soddisfare la relazione

Ci sono certo altri modi di procedere e sarebbe interessante confrontarli tra loro. Dateci dentro !...
maurizio

14/01/2017 at 12:23

Mi era sfuggito un particolare importante: il testo della domanda dice chiaramente che i risultati da ricercare devono essere numeri interi.

Partendo dall'esempio di Quazel, la terna pitagorica 3,4,5 può essere una matrice da cui derivare infinite soluzioni, semplicemente moltiplicando i tre valori per un stesso numero intero.

Così avremo 6,8,10, e poi 9,12,15, eccetera..

Naturalmente tutti i triangoli non sono altro che lo stesso triangolo rettangolo amplificato, quindi, anche se numericamente infiniti, sono solo una parte di tutte le forme che potremmo immaginare come descritto nel precedente post. Non mi soddisfa dire che sono infiniti solo per questo motivo....

Tornando ai triangoli costruiti nel cerchio, con cateti corrispondenti al seno e al coseno, i valori non sono numeri interi, quindi non rispondono alla domanda. Tuttavia potremmo pensare di moltiplicare per una opportuna potenza di 10 i valori di seno e coseno in modo da renderli interi.

Un esempio: se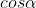 $cos\alpha$ = 0,8 allora 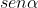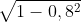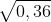$sen\alpha$ = $\sqrt{1-0,8^{2}}$ = $\sqrt{0,36 }$ = 0,6

Se moltiplico per 10 questi valori ottengo 8 e 6 (interi), i cui quadrati sommati danno 10. Per ciascun angolo posso procedere nello stesso modo, ovviamente usando potenze di 10 adeguate a ciascun caso.

Naturalmente nell'intervallo di valori tra zero e uno ci sono infiniti numeri di ogni tipo: razionali, irrazionali, periodici... solo una parte di essi è riconducibile nel modo descritto a valori interi. Un facile esempio è il caso di $\alpha$ = 45° che corrisponde a valori di seno e coseno uguali a 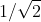$1/\sqrt{2 }$ tipicamente irrazionale.

Chi mi aiuta a dimostrare ai maghi e a Quazel che tolti i numeri non "interizzabili" nell'intervallo 0-1 , ne resta comunque un numero infinito? Dai....!
maurizio

15/01/2017 at 10:49

Va bene... abbiamo letto in molti queste parole.... che potrebbero darci una ispirazione:

Vedremo cosa si inventa Cantor per dimostrare che i numeri razionali (le frazioni) sono tanti quanti i numeri naturali (0,1,2,3,4,5,...), fra l'altro restando sorpreso egli stesso del risultato.

Sono contenute in questa pagina:

http://www.infinitoteatrodelcosmo.it/2016/03/27/un-nuovo-argomento-nell-infinito-teatro-del-cosmo-le-matematiche-pure/

Non ho finito di leggere tutti gli articoli che (con grande eleganza) Umberto ha scritto per noi, ma ne sono in un certo senso contento, perché mi dispiacerà quando sarà arrivato a completarli e non ne avrò di nuovi da leggere su questo argomento. Ma sono sicuro che avrà molte altre cose da proporre.
maurizio

17/01/2017 at 12:32
1. Prima che scada il tempo, propongo un ragionamento intuitivo , dando per scontato alcune affermazioni che forse andrebbero dimostrate.
2. Esistono infiniti numeri interi
3. Ciascun numero intero, diviso per un qualsiasi intero più grande, costituisce una frazione che rappresenta un numero razionale nell'intervallo aperto 0 1, in cui esistono infiniti numeri razionali.
4. Il rapporto tra due numeri razionali, in tale intervallo è un numero razionale.
Ora occorre fare riferimento alla figura al seguente link... (da cellulare non mi è possibile inserirla nel testo).

https://s27.postimg.org/ryucds36r/IMG_20170117_094216.jpg

Rappresenta il cerchio di raggio unitario e centro nell'origine degli assi, punto O (0,0).

Il raggio disegnato forma un angolo $\alpha$ con l'asse x.

Le sue proiezioni sugli assi x e y sono rispettivamente coseno e seno di $\alpha$ .

Il rapporto sen/cos è la tangente dell' angolo $\alpha$ .

Prolungando il raggio fino ad intercettare la retta tangente al cerchio nel punto P (1,0), ottengo il punto T . La distanza PT rappresenta il valore di tan $\alpha$ .

Se per l'angolo $\alpha$ assumo valori contenuti nell'intervallo aperto tra 0° e 45°, tan $\alpha$ avrà valori contenuti nell' intervallo aperto 0 1.

A ciascun valore razionale della tangente corrispondono valori razionali di seno (m/p) e di coseno (n/q).

Definisco con k=p*q il prodotto dei due denominatori. Esso è un intero.

Moltiplicando coseno e seno per k ottengo due numeri interi che chiamo. "a" e "b"

In pratica ho trasformato il triangolo rettangolo con ipotenusa=1 (raggio) e cateti coseno e seno di alfa, numeri razionali, in un triangolo simile i cui lati sono numeri interi a,b,k che formano una terna pitagorica.

Esistendo infiniti valori razionali per la tangente, esisteranno infiniti triangoli i cui lati costituiscono terne pitagoriche.

Nel caso che questo ragionamento, abbastanza farraginoso ed espresso in un linguaggio raggelante per un matematico, abbia senso, sarebbe certo meglio dargli una forma più rigorosa. E' questo però un compito che lascerei a chi, meglio di me, lo sa svolgere.
maurizio

18/01/2017 at 11:20

Nella soluzione proposta ieri ho trascurato un particolare importante: il valore razionale della tangente può derivare dal rapporto tra valori irrazionali di seno e coseno.

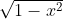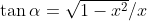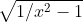Infatti, ponendo cos $\alpha$ =x e sen =y. posso scrivere y= $\sqrt{1-x^{2 }}$ e poi $\tan \alpha = \sqrt{1-x^{2}}/x$ = $\sqrt{1/x^{2}-1}$ ora, se sotto radice abbiamo un quadrato perfetto, la tangente è un numero razionale intero. Ma sono sicuro che anche seno e coseno siano razionali? La risposta è no.

Esprimendo coseno e seno in funzione della tangente, al denominatore di ambedue compare la radice di un quadrato perfetto + 1 che non può essere un quadrato perfetto. Perciò la radice resta e i due numeri sono irrazionali. Questo vale per tutti i valori interi della tangente, quindi in un numero infinito di casi.

Affrontiamo allora il problema in un modo diverso.

Quello che cerchiamo sono tutte le combinazioni di seno e coseno ambedue razionali e la dimostrazione che sono in numero infinito.

Consideriamo ancora il raggio del cerchio che parte dal punto O e raggiunge la circonferenza formando un angolo alfa con le ascisse. Esiste certamente un valore di alfa per il quale seno e coseno sono razionali ed è proprio quello che caratterizza la terna pitagorica 3 4 5. Dividendo ciascun numero per il maggiore dei tre, ottengo 3/5 4/5 5/5 tre numeri razionali che corrispondono a seno coseno e raggio unitario.

Per ottenere un secondo triangolo i cui cateti (seno e coseno) sono razionali basta duplicare alfa. Infatti i valori di seno e coseno di 2*alfa si derivano facilmente da quelli di alfa con operazioni di somma e prodotto tra numeri razionali i cui risultati sono anche essi razionali.

Graficamente ho riportato sulla circonferenza un arco identico e consecutivo a quello di alfa.

Dai valori razionali di seno e coseno passo quindi a valori proporzionali interi nel modo già illustrato, ottenendo una nuova terna pitagorica.

Il procedimento può essere ripetuto indefinitamente dando origine a infinite terne pitagoriche.

Naturalmente più che i valori di seno e coseno, che possono essere di segno negativo, dobbiamo considerare i loro valori assoluti, dato che i lati dei triangolo sono distanze sempre positive.
Vincenzo Zappalà

19/01/2017 at 11:03

Beh... nessun mago commenta?

Maurizio merita un qualche sostegno...

Lascia un commento Cancel Reply

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.

QUIZ: Pitagora a n dimensioni

Articoli correlati

Il Problema di Apollonio e le "sue" coniche. 3 **/***

Il Problema di Apollonio e le "sue" coniche. 2 **/***

Un grillo innamorato, Fibonacci e la prosodia indiana **

Il problema di Apollonio e le "sue" coniche. 1 **/***

14 commenti

Lascia un commento Cancel Reply

Il Problema di Apollonio e le "sue" coniche. 3 /*

Il Problema di Apollonio e le "sue" coniche. 2 /*

Il problema di Apollonio e le "sue" coniche. 1 /*