Soluzione del quiz della torta e del triangolo ***
Riporto la soluzione (personale) del quiz relativo alla torta inscritta in un triangolo. Arturo aveva trovato una soluzione, ma quella da me riportata utilizza solo la funzione seno e, quindi, la reputo, magari sbagliando, più "semplice". Sono stati aggiunti alcuni grafici che potrebbero scatenare le solite e bellissime animazioni...
Disegniamo subito la Fig. 1.
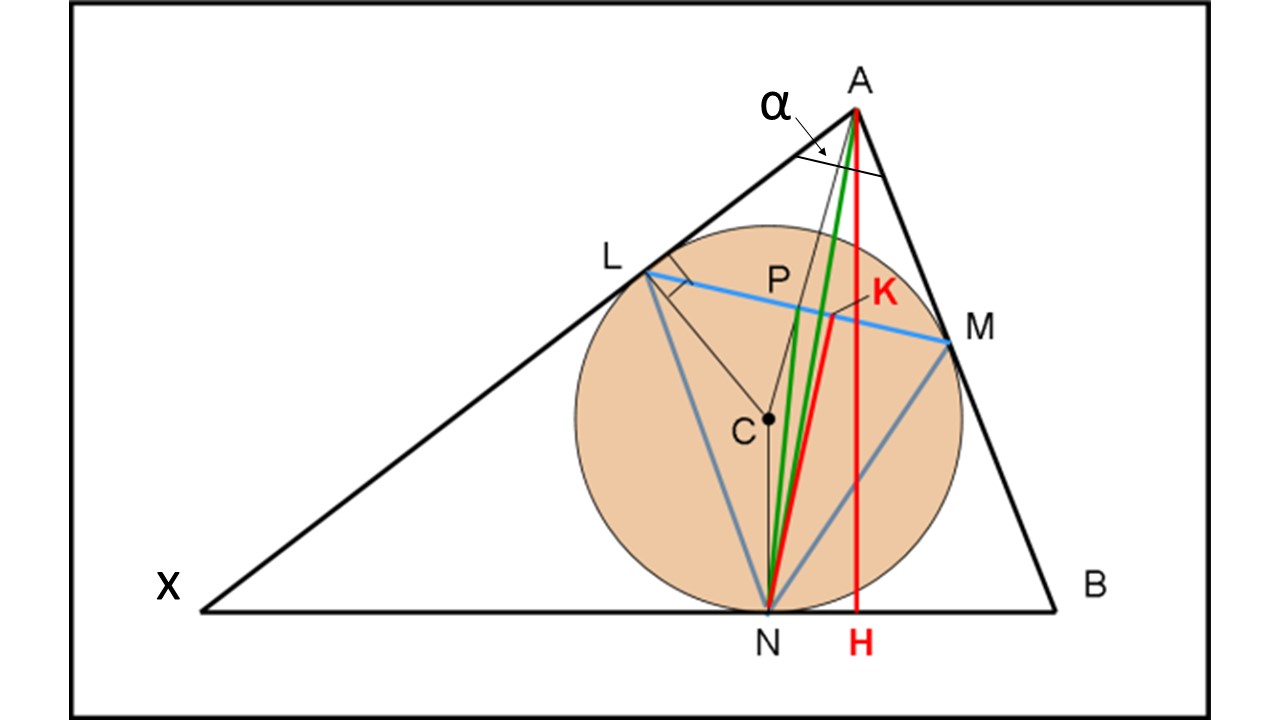
Chiamiamo α l’angolo XAB. Tracciamo il raggio CL, quello CM e congiungiamo C con A.
Si può concludere subito che l’angolo LPA è retto. Tuttavia, per i meno esperti dimostriamolo con pochi passaggi:
Per costruzione l’angolo CLA è retto (il raggio è perpendicolare alla tangente), così come CMA.
I triangoli CLA e CMA sono perciò uguali, dato che hanno due lati uguali (uno è in comune e l’altro è il raggio) ed entrambi un angolo retto. Ne segue che:
LA = AM
LAP = MAP = α/2
Consideriamo il triangolo LAM. Esso è isoscele (LA = AM) e vale la relazione tra gli angoli:
AML + ALM + α = 180°
Ma AML = ALM, e quindi:
2 AML + α = 180°
Dividendo per 2, si ha:
AML + α/2 = 90°
Ne segue che LPA = 90°, dato che la somma dei tre angoli del triangolo LPA devono essere 180°. Ossia:
AML + α/2 + LPA = 180°
90 + LPA = 18o°
Dedichiamoci al triangolo rettangolo CLA. Abbiamo appena dimostrato che CP è la proiezione di LC sull’ipotenusa CA. Possiamo tranquillamente applicare il primo teorema di Euclide che dice che un cateto è medio proporzionale tra la sua proiezione sull’ipotenusa e l’ipotenusa. Ossia:
CP : CL = CL : CA
Ossia:
CL2 = CP ∙ CA
Tuttavia CL = CN (entrambi raggi) e quindi:
CN2 = CP ∙ CA o ancora:
CN : CP = CA : CN …. (1)
Abbiamo anche una ovvia uguaglianza tra angoli:
ACN = PCN …. (2)
Anzi, è addirittura lo stesso angolo!
Dedichiamoci, allora, a due triangoli molto stretti, ma fondamentali: NCP e NPA. Anche se non sembra, essi sono simili, proprio per la (1) e la (2).
Guardiamo meglio la situazione nella Fig. 2, dove abbiamo disegnato solo i due triangoli, separandoli tra loro e ruotandone uno. In questo modo la similitudine risulta ben più evidente!
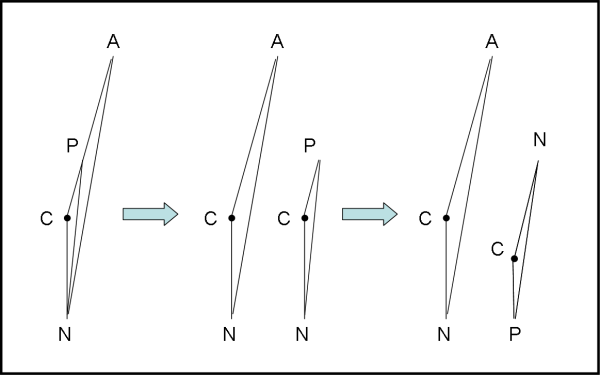
Utilizziamo di nuovo l’uguaglianza tra CN e CL e la (1) si può scrivere:
CL/CP = CA/CL
Dalla similitudine dei due triangoli NCP e NPA si ha anche che:
CP/CL = CL/CA = PN/AN …. (3)
Dal triangolo rettangolo CLA abbiamo che:
CL = CA sen(α/2)
E dalla (3):
PN/AN = sen(α/2) …. (4)
Dagli ormai famosi triangoli simili NCP e NPA, abbiamo anche l’uguaglianza di altri due angoli:
CPN = CNA
A questo punto traffichiamo con un paio di angoli:
NPM = CPM - CPN = 90 - CPN
ANB = CNB - CNA = 90 - CNA
Ma CPN = CNA e, quindi:
NPM = ANB (*)
Possiamo finalmente passare alle nostre altezze AH e NK.
Dal triangolo rettangolo PKN:
NK = PN sen(NPM)
E, dal triangolo rettangolo AHN:
AH = AN sen(ANB)
Ma NPM = ANB (*)
Da cui:
NK/AH = PN/AN
Dalla (4), si ha, finalmente:
NK/AH = sen(α/2)
Pappo ha eseguito questo calcolo e, quando si è trovato davanti alla torta, non ha dovuto fare altro che misurare l’angolo α, dividerlo per 2 e calcolarne il seno. Un’operazione che comporta solo pochi secondi.
Dato che il rapporto dipende solo da α, se non viene cambiato il punto A e non viene spostata la torta, il rapporto rimane sempre lo stesso, comunque sia tracciato il lato BC. Se viene spostato il punto A, basta che Pappo misuri nuovamente l’angolo α.
Ancora una volta Pappo riesce a risolvere il problema e a mangiarsi tutta la torta. Cosa che non fa mai, lasciando, comunque, una bella fetta al fratello…
Qualche grafico in più…
Si può illustrare come si manifesta la costanza del rapporto, cambiando prima l’angolo α e poi lasciando fisso l’angolo e cambiando l’inclinazione del lato BC. Per mostrare al meglio il rapporto tra le due altezze ho preferito usare i segmenti PN e AN che hanno lo stesso rapporto di NK e AH.
Consideriamo in Fig. 3 un triangolo molto semplice (isoscele) che non cambia la generalità della situazione.
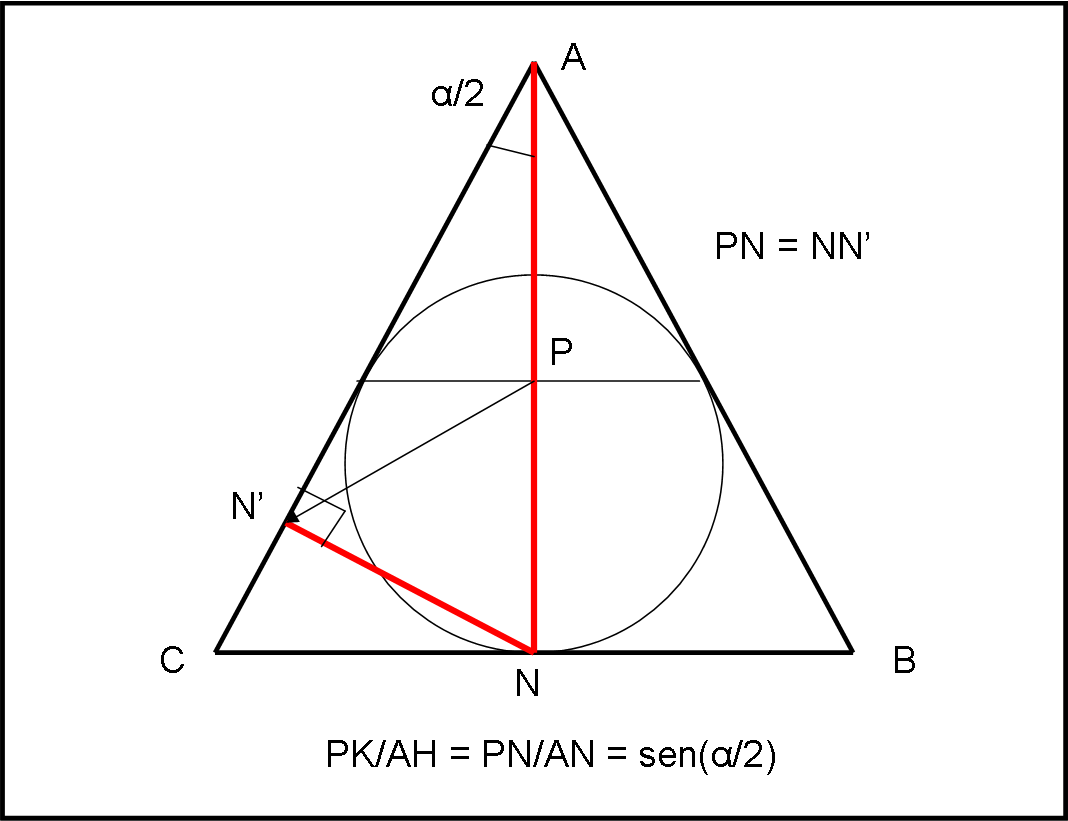
In questo caso PN e AN coincidono proprio con NK e AH della fig. 1. L’operazione da svolgere per vedere meglio la relazione tra PN e AN è costruire un triangolo rettangolo che abbia AN come ipotenusa e PN come cateto, il cui angolo opposto sia proprio α/2, L’operazione è estremamente semplice. Si ruota PN attorno a N fino a incontrare AC in N’ (ossia PN = NN’). L’angolo NN’A deve essere retto affinché valga quanto dimostrato precedentemente.
A questo punto (Fig. 4), spostiamo il cerchio-torta in modo che vari l’angolo α ed eseguiamo la stessa operazione di prima per ogni caso riportato. Per semplicità non abbiamo disegnato l’intero triangolo.
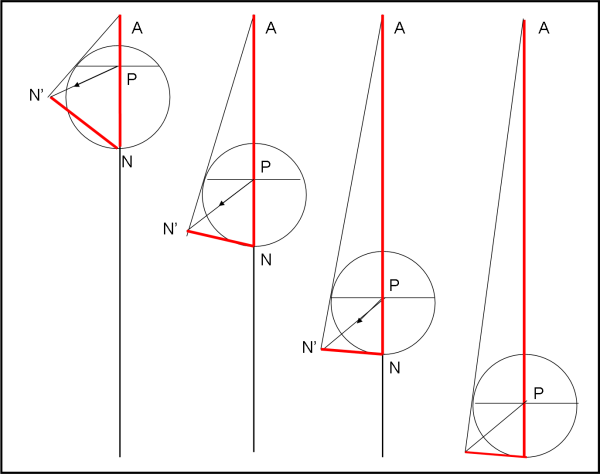
Si vede molto bene come varia il triangolo rettangolo rosso e come si arriva facilmente ai casi limite…
Passiamo, adesso, al caso in cui l’angolo α rimanga costante e vari il lato BC . In tal modo si sono trattati tutti i casi possibili. Partiamo da un triangolo decisamente diverso da quello isoscele usato prima (Fig. 5).
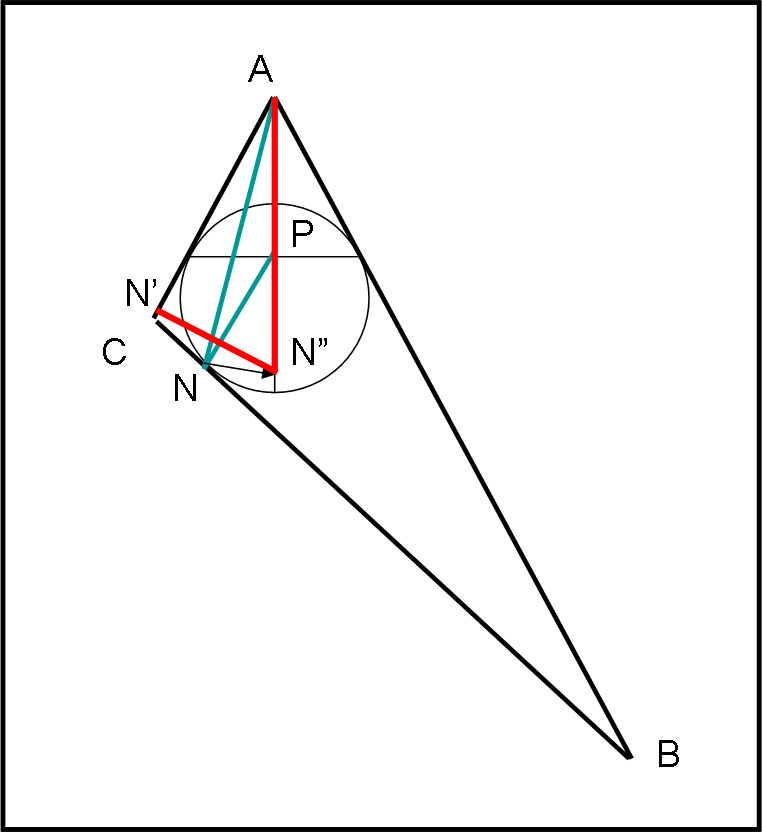
I segmenti che ci servono per rappresentare il rapporto tra PN e AN sono tracciati in blu. L’operazione da svolgere è leggermente più complicata. Riportiamo AN sulla retta identificata da AP e sia AN” = AN. Da N” tracciamo la perpendicolare ad AC che individua il punto N’. Per quanto dimostrato precedentemente deve essere N”N’ = PN. Il triangolo rettangolo rosso AN’N” è il triangolo che serve per individuare immediatamente il rapporto tra i segmenti PN e AN.
La Fig. 6 illustra tre triangoli diversi che abbiano l’angolo in A uguale ad α. Il primo triangolo coincide, ovviamente, con quello di Fig. 3. Anche in questo caso si trovano facilmente i casi limite.
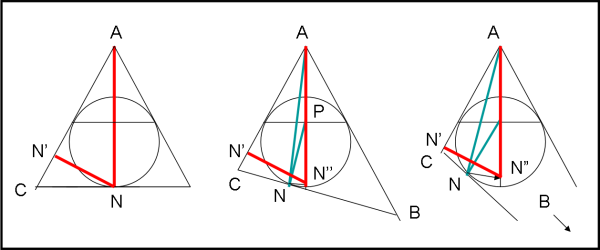
Questi ultimi grafici lasciano spazio a ulteriori generalizzazioni e ad animazioni varie. Chi vuole divertirsi può proseguire…
Il QUIZ lo trovate QUI
QUI trovate molti altri quiz, di vari livelli di difficoltà.






7 commenti
"Abbiamo anche una ovvia uguaglianza tra angoli:
APN = PCN …. (2)"
Naturalmente dovrebbe essere "ACN = PCN"
Io non avrei mai intravisto quei due triangoli, neanche dietro promessa di sfamarmi di torte mimose per sempre
grazie Arturo! Sì, non sono proprio immediati... ma, secondo me, mi scappa ancora qualcosa. La similitudine di quei due triangoli nasconde qualcos'altro... Boh... non sono riuscito a vederci niente, però sono sicuro che esiste...
Sai, Arturo, io credo che Enzo abbia analizzato a tappeto tutte le combinazioni di lettere a gruppi di tre, in modo da costruire tutti i triangoli possibili e poi abbia studiato tutte le coppie di questi triangoli, verificando la loro eventuale similitudine. Mi dice Oreste che è un metodo che usano anche quelli del CAC per ricostruire le dinastie dei faraoni partendo dai geroglifici disegnati sui muri delle piramidi. Dice che è un metodo "esaustivo" perché alla fine sei esausto.
Scherzi a parte complimenti per l'occhio di falco ( o di condor?) al nostro Enzo. Mi studierò con calma questi disegni per vedere se veramente nascondono ancora altro.
grazie Mau... sento puzza di qualcosa di più semplice... forse partendo dalla fine e tornando indietro...?
Comunque, Pappo potrebbe far parte del club dei maghi... che ne dite? Per lui una torta è come una carota messa davanti al muso dell'asino
Con il senno del poi, quando si sa già cosa cercare.
Chiamo con le lettere maiuscole ABC e LMN i vertici dei due triangoli, con le lettere greche corrispondenti gli angoli associati a ciscun vertice e con le lettere minuscole abc e lmn le lunghezze dei segmenti opposti al corrispondente vertice.
[caption id="" align="aligncenter" width="410"]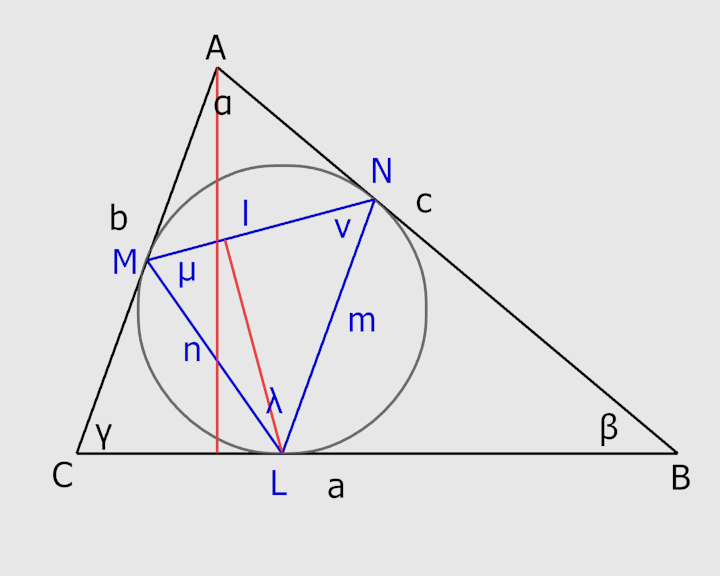 Figura 1[/caption]
Figura 1[/caption]
Le due altezze possono essere scritte come:
Questa seconda figura aiuta a trovare due relazioni che sono utile per sviluppare queste due formule.
[caption id="" align="aligncenter" width="416"]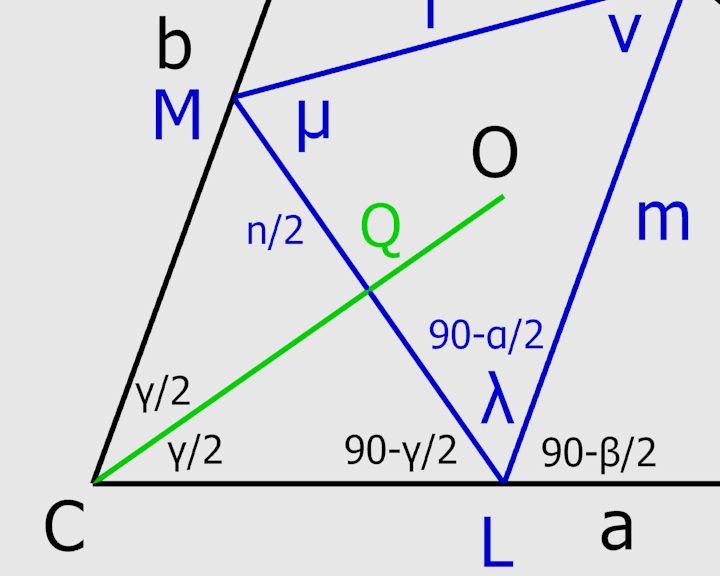 Figura 2[/caption]
Figura 2[/caption]
La prima è una relazione tra gli angoli del triangolo interno e gli angoli opposti del triangolo esterno.
In figura la vediamo per gli angoli lambda ed alfa, analogamente vale per tutti le coppie di angoli.
Il teorema dei seni}=\frac{m}{\sin(\mu)}=\frac{n}{\sin(\nu)}) può essere scritto facendo intervenire gli angoli esterni
può essere scritto facendo intervenire gli angoli esterni
La seconda è una relazione che lega i lati del triangolo interno con quelli del triangolo esterno.
In figura si vede che CM è l'ipotenusa del triangolo rettangolo CMQ. Applico la definizione di seno di un angolo come rapporto tra cateto opposto all'angolo ed ipotenusa ed ottengo:
Da queste si può ricavare che
Poiché nella espressione di h vista sopre appare m, conviene far apparire m anche in questa espressione utilizzando il teorema dei seni visto sopra dal quale ottengo&space;}}{\cos{\left(&space;\frac{\mathit{\ensuremath{\beta}}}{2}\right)&space;}}) e
e &space;}}{\cos{\left(&space;\frac{\mathit{\ensuremath{\beta}}}{2}\right)&space;}}) da cui
da cui
Ora abbiamo tutti gli elementi per tornare al rapporto H/h
bella Fabry... ma volevamo solo la funzione SENO...

In effetti, per trovare H/h ho usato qualche nozione di trigonometria in più.
Comunque il goniometro è usato per misurare un solo angolo e la calcolatrice per la sola funzione seno.