Qual è stato il primo computer nella storia dell’uomo? Si pensa quasi subito all’abaco e spesso ci si rifà ai greci, dimenticando -forse- che i cinesi lo usavano già da migliaia di anni. Non solo, però… Sembra che per effettuare le moltiplicazioni in modo rapido e sicuro si affidassero al Mikado, quel gioco con i bastoncini che noi chiamiamo Shangai. Oggi, è stato ripreso e chiamato “moltiplicazione giapponese”, ma l’origine sembra ben più antica. e diversa.

In realtà, non è un calcolatore meccanico, dato che deve essere l’uomo a eseguire i gesti per ottenere il risultato, ma il fatto di utilizzare qualcosa di artificiale per eseguire una moltiplicazione in modo molto rapido ci permette una piccola inesattezza.

Forse molti lo conoscono già, ma mi è sembrato interessante proporlo in modo estremamente schematico (come è in realtà) sia per “giocarci” un po’, sia per eliminare del tutto le tabelline pitagoriche (gioia e dolore dei bei tempi andati). Chissà che si inizi di nuovo a fare i conti da soli senza aspettare il risultato che ci regala con grande generosità un aggeggio elettronico?!

Tutto ciò ci ricorda un fantastico racconto di Asimov, dove nessuno sapeva più fare le operazioni senza l’uso delle macchine, finché … No, non voglio togliere il piacere di scoprirlo a chi non lo ha mai letto...

Torniamo alle nostre moltiplicazioni… e cominciamo proprio con le tabelline. Tre per cinque? Quindici, ovviamente (anche senza aiuto elettronico).

Facciamo l’operazione in altro modo, usando solo delle linee (Fig. 1).

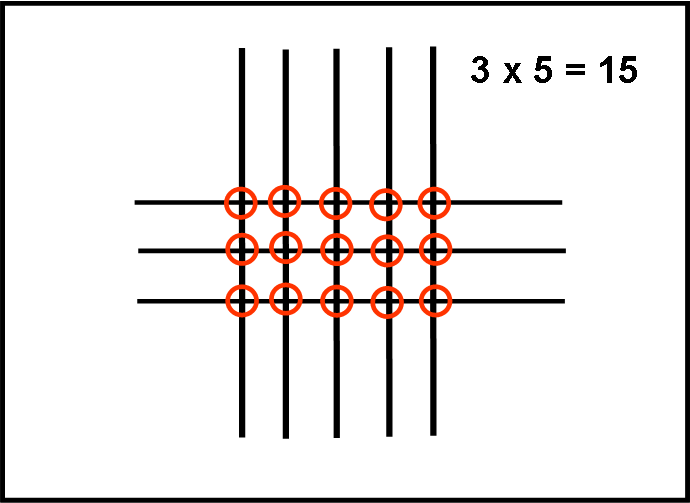
Il primo numero è TRE? Bene tracciamo tre linee orizzontali. Il secondo numero è CINQUE? Tracciamo cinque linee verticali. I due gruppi di linee parallele si intersecano. Bene, contiamo le intersezioni… uno, due, tre, …, quattordici, QUINDICI. D’altra parte potevano aspettarcelo, dato che la moltiplicazione non è altro che una somma: tre per cinque? Sommiamo tre cinque volte o -se preferiamo- sommiamo cinque tre volte.

Fin qui l’aiuto nella rapidità sembra poca cosa. Tuttavia, il metodo dei “bastoncini” permette di fare moltiplicazioni ben più complicate, sempre e soltanto sommando dei numeri, ma in modo decisamente più rapido. Se chiedessi quanto fa 13 moltiplicato 123, penso che ben pochi abbiano voglia di sommare 123 volte il numero 13. E non parliamo di moltiplicazioni con numeri a 4 o 5 cifre… Quanto fa 1234 moltiplicato 5432? Voglio vedere qualcuno che si mette a sommare 1234 ben 5432 volte!

Introduciamo, allora, la moltiplicazione cinese. Facciamolo in modo estremamente “ordinato” anche se, poi, con un po’ di esperienza, il tutto può essere fatto con maggiore velocità e senza schemi prestabiliti…

Cominciamo con il caso più semplice che è poi facile allargare: consideriamo solo le moltiplicazioni di numeri con doppia cifra. Disegniamo un quadrato diviso sia orizzontalmente che verticalmente in due sezioni (Fig. 2).

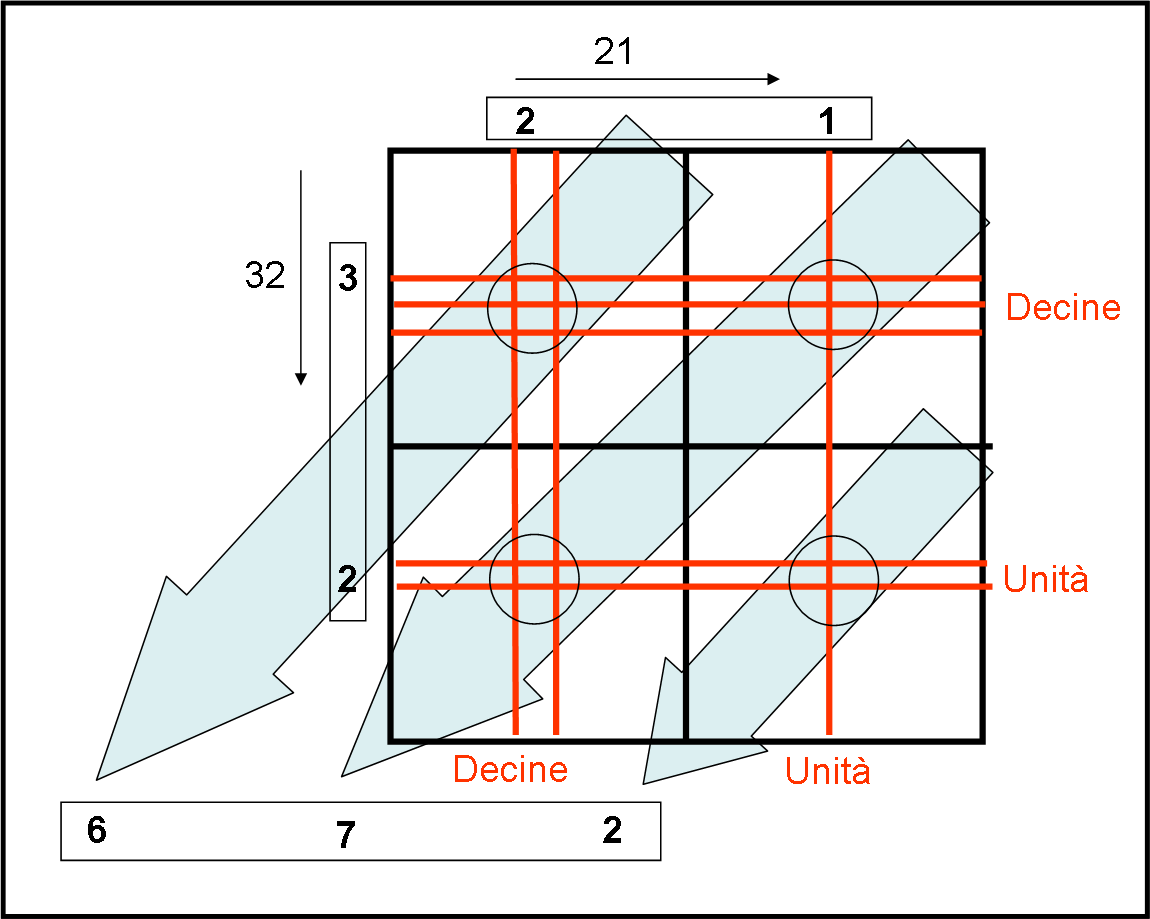
Il primo numero viene rappresentato nelle sezioni orizzontali. In quella superiore mettiamo le decine e in quello inferiore le unità. La novità è che non scriviamo le cifre, ma inseriamo delle righe orizzontali (rosse) in numero uguale alle decine  e alle unità… Ad esempio scriviamo il numero 32. Le unità sono 2 e tracciamo 2 linee nella sezione orizzontale delle unità. Le decine sono 3 e inseriamo 3 linee nella sezione orizzontale delle decine.

Passiamo, adesso al secondo numero che vogliamo moltiplicare per il primo. Sia, ad esempio, 21. Le sue cifre (rappresentate come linee verticali) vengono inserite nelle sezioni verticali, le unità a destra e le decine a sinistra.

Non ci resta, adesso, che tracciare delle frecce (azzurre leggere), inclinate di 45° che taglino i quadrati formati dalle varie sezioni di partenza. Possiamo disegnarne tre. Ogni linea così tracciata ci dà la cifra della moltiplicazione a partire da quella più a destra (unità) fino a quella più a sinistra (centinaia). Come ricavare la cifra esatta? Basta sommare per ogni linea azzurra il numero di INCROCI delle linee rosse tra di loro. Cominciando dal basso a destra: la linea azzurra incontra un solo gruppo di incroci (quello relativo alle unità dei numeri di partenza). Quanti incroci abbiamo? 2 e questa cifra rappresenta quella delle unità del risultato.

Spostiamoci alla linea azzurra di mezzo. Essa incontra due gruppi di incroci (quello relativo alle unità e quello relativo alle decine dei numeri originali). Basta contare gli incroci: 3 nella parte alta a destra e 4 nella parte bassa a sinistra. Il totale è 3 + 4 = 7. Questa è la seconda cifra che ci serve, quella delle decine.

Rimane ancora la terza linea azzurra, quella che si riferisce alle intersezioni delle decine di partenza. Quanti incroci ci sono? 6. Questa è la terza cifra che cercavamo, quella relativa alle centinaia. Il numero finale è quindi: 672, proprio il risultato della moltiplicazione di 32 per 21.

Ovviamente, non è necessario fare tutte le volte il quadrato originario, ma basta tracciare le linee separate da un certo spazio, come rappresentato in Fig. 3, dove abbiamo già inserito il posto per numeri di quattro cifre. Anche le linee a 45° possono essere tracciate velocemente. L’importante è, però, che contengano i gruppi di incroci corrispondenti (non perdiamone qualcuno per strada).

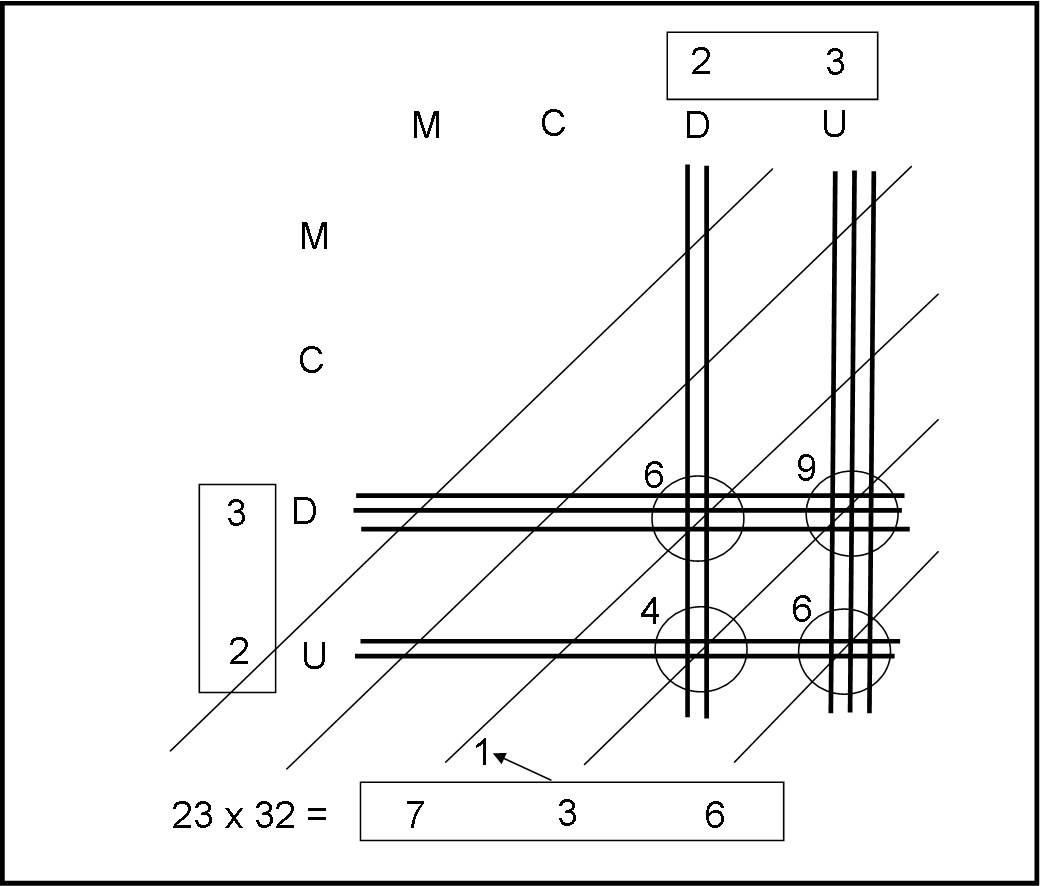
Eseguiamo la moltiplicazione 23 per 32. Tutto va avanti come prima, tranne un’ovvia difficoltà (che dovevamo aspettarci): sommando 9 e 4 incroci (seconda linea a 45° da destra) otteniamo 13. Nessun problema, scriviamo 3 e riportiamo 1 nella riga inclinata successiva. Questo 1 lo sommeremo agli incroci della riga corrispondente.

Facciamo un’ulteriore esempio nella Fig. 4 (numeri con tre cifre), in cui capita che vi sia una cifra uguale a ZERO.

Non spaventiamoci e tracciamo la sua linea corrispondente come tratteggiata (ad esempio). La sua presenza annulla tutti i suoi incroci. Eseguiamo la moltiplicazione 102 per 322.

Resta ancora un piccolo trucco che si può utilizzare, per non appesantire troppo la figura. Quando una cifra è superiore a 5 si può tracciare una linea di colore diverso che comporti 5 incroci ad ogni suo incontro con un'altra linea. Lo vediamo nella Fig. 5 dove moltiplichiamo 12 per 172. Il 7 è stato tracciato come due linee normali e una blu, che rappresenta il 5. Come si nota, nella moltiplicazione abbiamo dovuto, inoltre, riportare due volte la cifra 1.

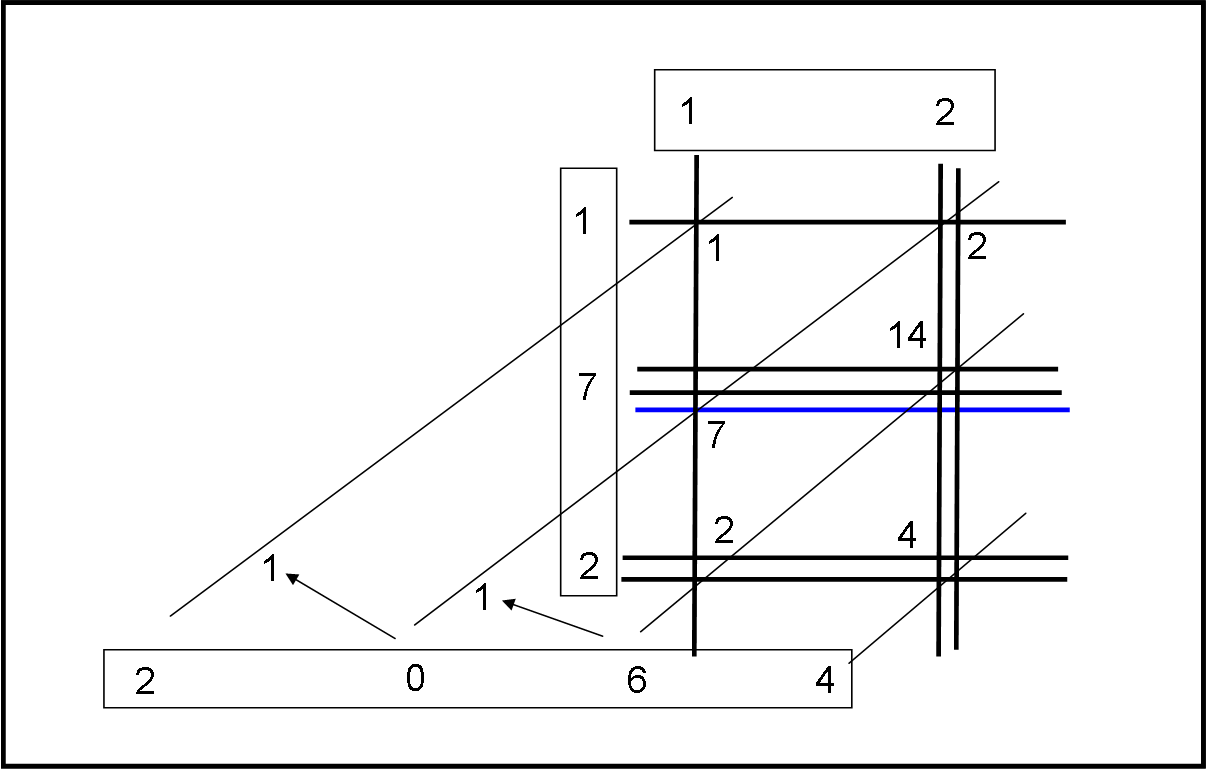
A questo punto potete divertirvi da soli, aumentando di quanto volete le cifre dei due numeri da moltiplicare. Cercate di non confondervi con i gruppi di incroci da sommare tra loro e … buttate pure via le calcolatrici elettroniche!