Categorie: Articoli Curiosità Matematica
Tags: matematica metodo cinese metodo contadini russi metodo egizio moltiplicazione moltiplicazione in colonna prodotto
Scritto da: Arturo Lorenzo
Commenti:2
Moltiplicazioni: metodi alternativi *
A tutti noi, quando abbiamo frequentato le scuole elementari, è stato insegnato come eseguire la moltiplicazione. Il metodo adottato è quello della moltiplicazione in colonna. Pare che nel Rinascimento questo metodo fosse conosciuto in Toscana come metodo "per bericuocolo", dal nome dei tipici dolcetti della zona ora noti come "cavallucci", mentre a Venezia come metodo "per scacchiere" e a Verona come metodo "per organetto". In sostanza, si prendono i due numeri coinvolti nella moltiplicazione, moltiplicando e moltiplicatore, si scrivono uno sopra l'altro , allineandoli a destra in maniera che le unità del primo numero siano incolonnate con le unità del secondo. Sopra ci mettiamo il moltiplicando e sotto il moltiplicatore. Naturalmente, per la proprietà commutativa di cui gode la moltiplicazione, possiamo scegliere come vogliamo quale dei due numeri sarà il moltiplicando e quale il moltiplicatore, ottenendo in ogni caso lo stesso risultato. Si inizia a moltiplicare la cifra delle unità del moltiplicatore per ciascuna delle cifre del moltiplicando, partendo da quella delle unità. Se il risultato di ciascuno di tali prodotti risulta minore di dieci, si scrive direttamente il risultato sotto la linea di separazione. Se, invece, risulta maggiore o uguale a dieci, sotto la linea di separazione si scrive solo la cifra delle unità del risultato, mentre la cifra delle decine si riporta e si somma al prodotto successivo. Una volta esaurite come sopra le moltiplicazioni tra cifra delle unità del moltiplicatore e le cifre del moltiplicando, ci ritroveremo, sotto la linea di separazione, quello che definiamo prodotto parziale. A questo punto, ripetiamo l'operazione suddetta con la cifra delle decine del moltiplicatore. Cioè, moltiplichiamo la cifra delle decine del moltiplicatore per ciascuna delle cifre del moltiplicando, seguendo lo stesso metodo visto prima. Cominceremo, però, a scrivere i risultati di tali prodotti spostandoci di una colonna verso sinistra, lasciando , cioè, libero, uno spazio sotto la cifra delle unità del primo prodotto parziale. Ripetiamo l'operazione anche per la cifra delle centinaia del moltiplicatore e così via. Alla fine, avremo trovato tanti prodotti parziali quante sono le cifre del moltiplicatore e ciascuno di essi spostato verso sinistra di un posto. Andremo a sommare in colonna i suddetti prodotti parziali ottenendo infine il risultato della moltiplicazione di partenza. Naturalmente, poiché nella procedura è previsto di eseguire diversi prodotti tra le varie cifre dei due numeri, è necessario conoscere le tabelline.
Ormai applichiamo la suddetta procedura in modo meccanico, senza rammentare che dietro ad essa vi sono , naturalmente, strutture formali di supporto. Quando moltiplichiamo in colonna due numeri, infatti, senza rendercene conto, utilizziamo alcune fondamentali proprietà di cui godono le operazioni della somma e del prodotto, in particolare la proprietà commutativa della somma e del prodotto nonché la proprietà distributiva del prodotto sulla somma.
Ma esistono metodi di moltiplicazione manuali alternativi a quello in colonna sopra illustrato e che non richiedano la conoscenza delle tabelline ? Sicuramente il metodo in colonna è molto efficace ed applicabile nella generalità dei casi. Tuttavia, nel corso della sua storia , l'uomo ha inventato metodi a volte curiosi , ma non meno efficaci, per trovare il risultato di una moltiplicazione. Ne esaminerò alcuni che mi hanno particolarmente incuriosito, cercando di spiegarne il funzionamento.
Metodo cinese (o grafico)
Uno di questi, certamente ad effetto per la sua veste grafica, è quello noto come metodo cinese. Ma altrove se ne parla come metodo grafico degli incroci o come metodo dei bastoncini. In rete lo si trova immortalato in innumerevoli video che ne parlano come metodo giapponese. Una peculiarità di questo metodo è che consente di eseguire le moltiplicazioni anche a chi non ricorda le tabelline. Basta, infatti, saper sommare. Nel nostro Circolo è già stato pubblicato da Vincenzo un articolo completo sul metodo , al quale rinvio per ulteriori approfondimenti. Ricordiamo qui in cosa consiste.
Supponiamo di voler moltiplicare il numero 312 per il numero 231. A ciascuna cifra del primo numero, cominciando da sinistra, si fanno corrispondere altrettante linee verticali sul foglio di carta. Quindi, nel caso in oggetto, disegneremo 3 linee verticali (corrispondenti alla prima cifra 3 del primo numero), poi, lasciando un po' di spazio, un'altra linea (corrispondenti alla cifra 1), e infine altre 2 linee (corrispondenti alla cifra 2). Stesso procedimento grafico per il secondo numero, con la differenza che stavolta le linee che disegneremo saranno orizzontali , dall'alto verso il basso e tali da incrociare quelle verticali disegnate prima. Quindi, nel caso in oggetto, disegneremo 2 linee orizzontali (corrispondenti alla prima cifra 2 del secondo numero), poi tre linee (corrispondenti alla cifra 3), e infine un'altra linea (corrispondente all'ultima cifra 1 del secondo numero). La figura seguente illustra il reticolo di linee così ottenuto. Le linee verticali rosse sono quelle relative alle cifre del moltiplicando (312) , mentre quelle orizzontali nere sono relative alle cifre del moltiplicatore (231)

A questo punto, individuiamo gli incroci tra gruppi di linee, partendo dall'angolo in basso a destra e procedendo poi verso sinistra. Nel caso in oggetto, i due numeri da moltiplicare hanno entrambi 3 cifre, quindi gli incroci tra gruppi di linee sono 9. In sostanza è come se avessimo a che fare con una matrice di 3 righe e 3 colonne. In ciascuna cella di tale matrice ci sono gli incroci tra gruppi di linee. Cominciando , allora, dall'angolo in basso a destra, contiamo i punti di intersezione tra le 2 linee verticali e l'unica linea orizzontale che vi si incrociano. Essi sono 2. Scriviamo tale numero in colore verde , ad indicare che è definitivo.
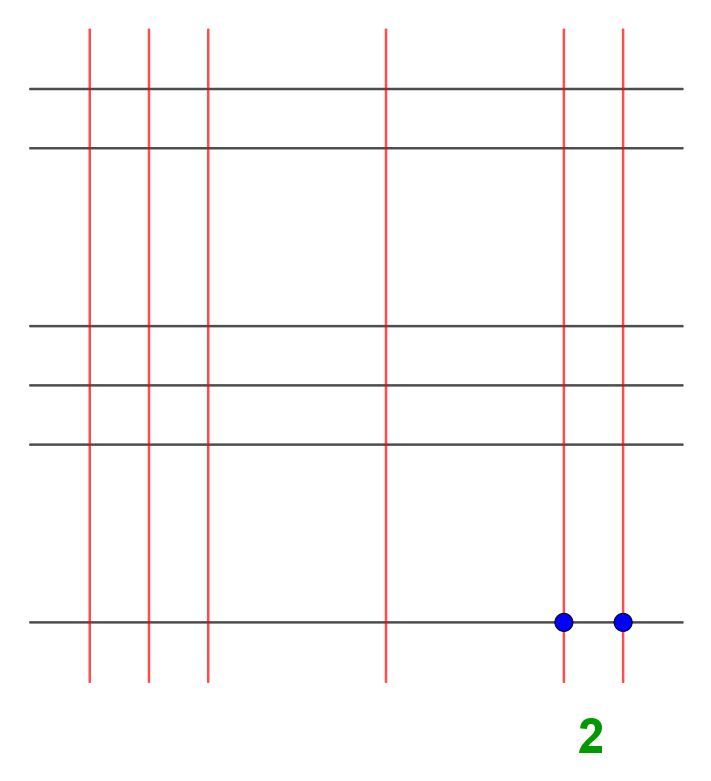
Si passa ora al successivo conteggio. Quali incroci devo considerare ? Devo considerare quelli a sinistra e in alto rispetto all'incrocio considerato prima. In pratica, basta seguire le direzioni diagonali tratteggiate indicate nella seguente figura.
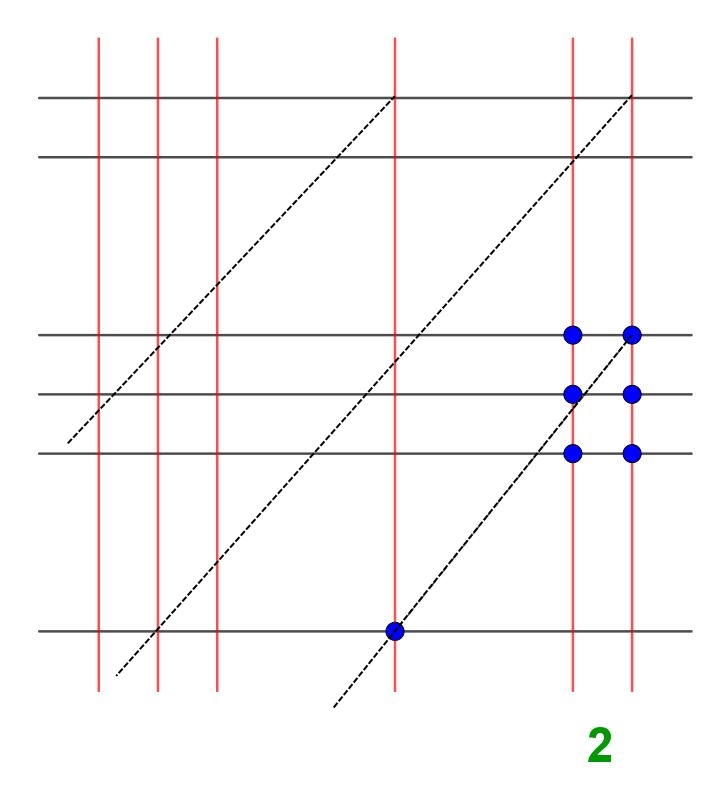
Come prima, contiamo le intersezioni , ottenendone sette (1+6). Anche questo numero 7 lo scriverò in verde, in quanto definitivo. Passo al successivo conteggio. Come prima, considero gli incroci di linee posti a sinistra e in alto rispetto a quelli considerati nel precedente conteggio. Stavolta i punti di intersezione in totale sono 10. In questo caso, scriverò in verde solo la cifra delle unità (in questo caso 0) , mentre la cifra delle decine (in questo caso 1) la scriverò in colore differente perché va riportata al conteggio successivo.
Procedendo come sopra, alla fine arriverò all'angolo in alto a sinistra della matrice di linee, avendo ottenuto , nel caso in oggetto, 5 cifre verdi. Leggendole da quella in alto a sinistra a quella in basso a destra, quello sarà il risultato della moltiplicazione !
Quella di seguito è una animazione che illustra l'intero procedimento.
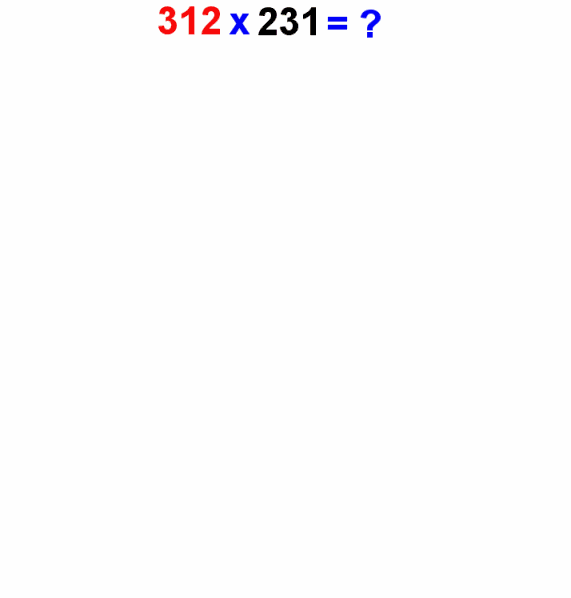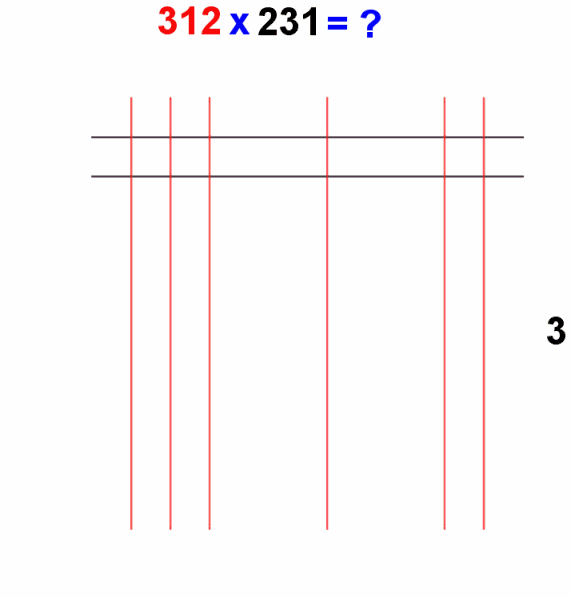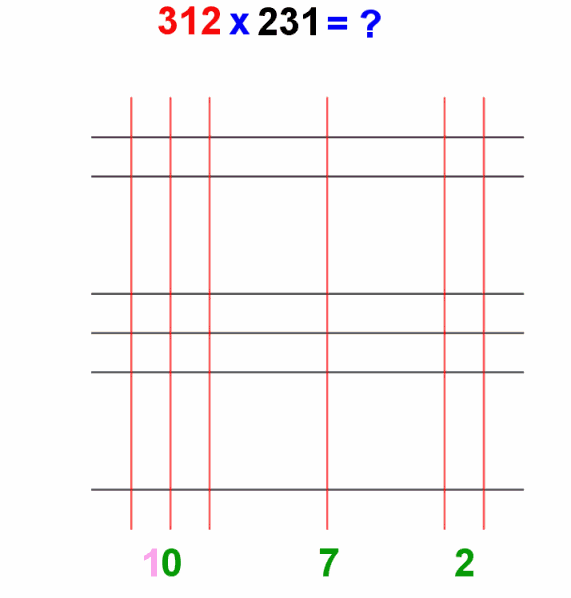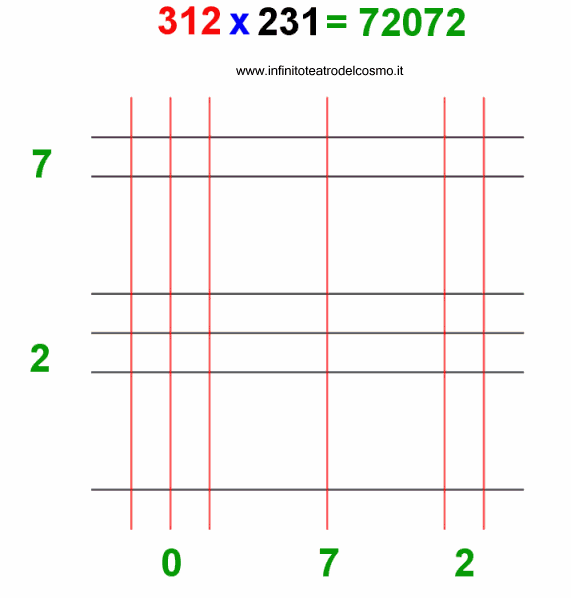
Come fa a funzionare ?
Il metodo cinese , in sostanza, sostituisce alla moltiplicazione di ciascuna cifra del secondo numero per ciascuna cifra del primo, la somma dei punti di intersezione tra i gruppi di linee corrispondenti alle cifre considerate. Per esempio, quando andiamo a contare i punti di intersezione tra le 2 linee verticali a destra e la linea orizzontale in basso, non stiamo facendo altro che trovare il risultato di 2x1. Anche i riporti incontrati durante la procedura non hanno alcunché di diverso dai riporti operati durante la moltiplicazione con il metodo tradizionale in colonna. La differenza sostanziale del metodo cinese, rispetto a quello tradizionale, è che con esso si evita la necessità di fare dei prodotti intermedi. Per calcolare il prodotto di 312 per 231, infatti, abbiamo eseguito solo delle somme. Chi non sa o non ricorda le tabelline è salvo.
E' facile intuire che questo metodo va bene nel caso di numeri con cifre non troppo alte. Se, ad esempio, volessimo moltiplicare utilizzando questo metodo i numeri 9786 e 7695 , verrebbe fuori una costruzione grafica davvero importante (30 linee verticali per il primo numero e 27 orizzontali per il secondo, con un totale di ben 810 punti di intersezione). La probabilità di sbagliare nel conteggio dei punti di intersezione aumenterebbe notevolmente.
Metodo egizio ( o dei raddoppi)
Presso l'antica civiltà egiziana la moltiplicazione veniva eseguita applicando un metodo numerico basato sui raddoppi successivi. Sono giunte fino a noi testimonianze di tale metodo attraverso importanti documenti matematici egizi come il papiro di Rhind, risalente al 1650 a.C. circa , opera di uno scriba che lo trascrisse da un papiro ancora precedente, risalente al 2000 a.C.
Come si esegue la moltiplicazione con tale metodo ? Si formano due colonne. In quella di sinistra si fanno i raddoppi successivi partendo da 1 fino al massimo valore che non superi il moltiplicando. Nella colonna a destra si fanno i raddoppi successivi del moltiplicatore. Supponiamo di voler moltiplicare 153 per 241. Sia 153 il moltiplicando e 241 il moltiplicatore. Avremo nella colonna di sinistra i valori, ottenuti partendo da 1 raddoppiando ogni volta:
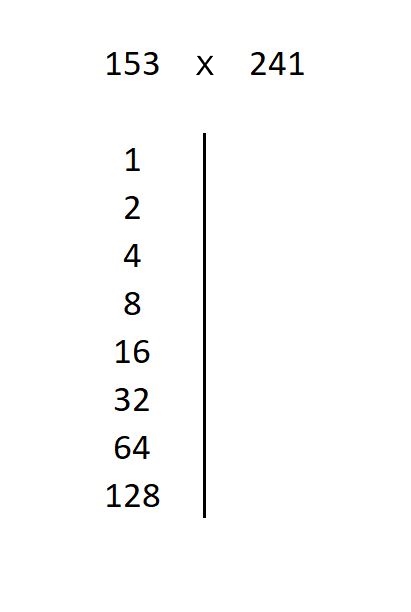
Ci fermiamo a 128 perché, raddoppiando ancora otterremmo 256, che è maggiore del moltiplicando. Nella colonna di destra, invece, avremo i valori ottenuti partendo dal moltiplicatore e raddoppiando ogni volta. Ci fermeremo quando avremo raggiunto l'ultima riga della colonna di sinistra:

E' il caso di notare che il raddoppio, anche di numeri a più cifre , è più agevole di una generica moltiplicazione perché si può ottenere addizionando a sé stesso il numero da raddoppiare. A questo punto, con riferimento alla colonna di sinistra, scegliamo i valori che sommati tra loro ci danno come risultato il moltiplicando:
128+16+8+1 = 153
In corrispondenza di tali valori leggiamo i corrispondenti valori nella colonna di destra e li sommiamo:
30848+3856+1928+241 = 36873
Questo è il risultato della moltiplicazione 153 x 241 ! Anche con questo metodo, non è necessario conoscere le tabelline, basta saper raddoppiare e sommare.
Ma come mai sommando i valori visti prima otteniamo proprio il risultato della moltiplicazione ? Basta soffermarsi su cosa è stato fatto. Abbiamo inizialmente espresso il moltiplicando come somma di potenze del 2. Infatti:
(3)
Poi abbiamo letto i valori corrispondenti sulla colonna del moltiplicatore. Ma, poiché tali valori sono corrispondenti a quelli della colonna a sinistra e sono ottenuti raddoppiando il moltiplicatore partendo dall'alto verso il basso, risulta evidentemente:
Quindi, quando sommiamo i suddetti valori otteniamo:
cioè, per la proprietà distributiva:
cioé, per la (3):
ossia proprio il prodotto cercato.
Metodo dei contadini russi ( o dei raddoppi e dimezzamenti)
Un antichissimo proverbio dice, a proposito dei contadini, "scarpe grosse, cervello fino", per far intendere che , nonostante le calzature pesanti dovute al loro lavoro nei campi, spesso i contadini dimostrano acume e intelligenza. I contadini russi, a quanto pare, hanno manifestato un cervello particolarmente fino quando hanno inventato il metodo di moltiplicazione che porta il loro nome.
Il metodo somiglia a quello egizio. Anche con questo si scrivono due colonne di numeri, una per il moltiplicando e una per il moltiplicatore. La prima ottenuta raddoppiando il moltiplicando e la seconda dimezzando, stavolta, il moltiplicatore fino ad arrivare ad 1. Se dimezzando il numero viene fuori un resto, non lo prendiamo in considerazione. Un esempio chiarisce, come al solito, più di mille parole. Supponiamo di voler moltiplicare, anche stavolta, 153 per 241. Partiamo dalla colonna di destra, quella del moltiplicatore 241. In tale colonna scriveremo i valori, ottenuti partendo dal moltiplicatore e dimezzando ogni volta fino ad arrivare a 1. Quando dividiamo 241 per 2, il risultato sarebbe 120 con resto pari a 1. Nella colonna scriveremo solo il 120. Stesso discorso quando dividiamo per 2 il 15, il 7, il 3 e l'1.

Ora passiamo alla colonna di sinistra e andiamo a riempirla con i valori ottenuti partendo dal moltiplicando e raddoppiando ogni volta. Continueremo a raddoppiare fino a raggiungere la stessa lunghezza della colonna di destra (8 valori):
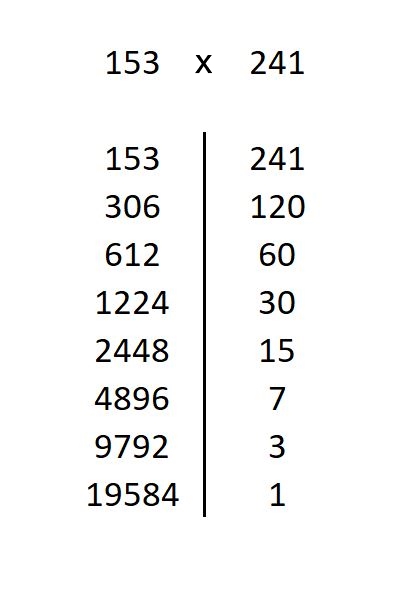
A questo punto, dei suddetti valori prendiamo in considerazione solo quelli corrispondenti a valori dispari della colonna di destra , li sommiamo e otteniamo il risultato della moltiplicazione:
153 (corrispondente a 241)
2448 (corrispondente a 15)
4896 (corrispondente a 7)
9792 (corrispondente a 3)
19584 (corrispondente a 1)
153+2448+4896+9792+19584=36873 (= 153 x 241 !)
Anche con questo metodo, si evita la conoscenza delle tabelline, essendo richiesto solo di saper raddoppiare e dimezzare i numeri.
E anche in questo caso, la spiegazione del metodo risiede nella scrittura del moltiplicatore in somma di potenze di 2:
(4)
Quando andiamo a sommare i valori presi dalla colonna sinistra corrispondenti a quelli dispari della colonna di destra, abbiamo:
che possiamo scrivere come:
cioè, per la proprietà distributiva:
e cioè, per la (4)
ossia proprio il prodotto cercato. Ma , quando individuiamo i valori della colonna di sinistra da sommare per ottenere il risultato, perché prendiamo in considerazione solo quelli corrispondenti ai valori dispari della colonna di destra ? Per comprenderlo, osserviamo che dimezzando iterativamente il moltiplicatore, in pratica lo stiamo convertendo in base 2 , partendo da base 10. Infatti, per scrivere un numero in base 10 nel suo corrispondente in base 2 , come noto, lo dobbiamo dividere iterativamente per 2 e considerare ogni volta l'eventuale resto. Nella seguente figura ho scritto, accanto a ciascun numero n , il resto della divisione n/2, indicandolo in rosso:
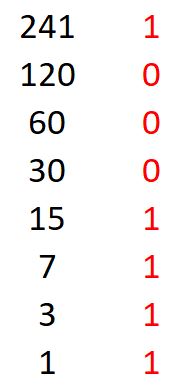
Il moltiplicatore, espresso in base 2, è dunque 11110001 . Volendo , poi, passare dalla base 2 alla base 10, applicando la formula polinomiale al moltiplicatore espresso in base 2 avremo:
Come si vede, sono solo i valori dispari che generano resto e quindi concorrono alla conversione del moltiplicatore in base 10. Sono, dunque, solo i valori dispari della colonna del moltiplicatore a dover essere presi in considerazione. I contadini russi, inconsapevolmente, applicavano una logica binaria per moltiplicare due numeri.
Conoscete altri metodi manuali e che non richiedano di ricordare le tabelline ? Menzionateli nei commenti.


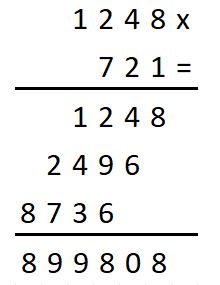




2 commenti
Interessantissimo. Non sapevo che esistessero tutti questi metodi...!
Questo più che un metodo è uno strumento, una specie di protesi degli ingegneri di un tempo lontano.