QUIZ geometrico: uno strano terreno **
Pippo, Pappo e Peppa si sono comprati degli appezzamenti di terreno per costruirsi tre casette separate. Purtroppo, la forma totale ABECD non è certo l’ideale per essere diviso equamente.
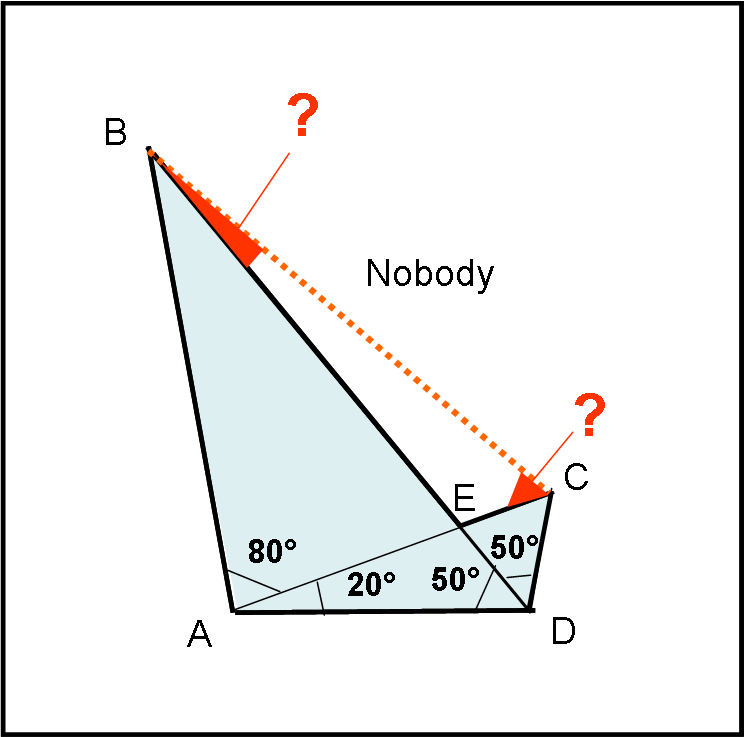
I nostri tre amici hanno già misurato tutti gli angoli più importanti e gliene mancano solo due, che non sembrano proprio mostrare grandi difficoltà di calcolo (ABE e BEA).
Prima di eseguire gli ultimi calcoli, ecco giungere, senza preavviso alcuno, il padrone del terreno che confina con i lati BE ed EC. Indovinate chi è? Sì, è lui, proprio lui… il malefico Prof. Nobody.
Il suo sorriso mefistofelico non lascia dubbi: ne sta preparando una delle sue…
Si rivolge ai nostri tra amici e dice: “Sono disposto a regalarvi una parte del mio terreno per aiutarvi nella divisione. Prima, però, dovrete risolvere un piccolo problema di geometria. Nel caso che non ci riusciate mi prenderò tutto il vostro terreno e mi costruirò un campo da golf! Accettate la proposta?”
Peppa, Pappo e Pippo ci pensano solo un attimo e poi all’unisono rispondono: “Sicuramente sì! Esponici il problema…”
“Bene” dice Nobody, “è molto semplice: tracciate il segmento BC e il triangolo BEC sarà vostro. Basta solo che mi diciate, senza fare calcoli trigonometrici e solo lavorando sulla mappa, quanto valgono gli angoli EBC ed ECB …”.
Pappo, Peppa e Pippo si mettono a ridere. Conoscono così tanti angoli che sarà veramente un gioco da ragazzi dare la risposta.
Ma è proprio così “facile?”. Forse no, anche se alla fine i nostri amici riescono a rispondere esattamente usando due strategie diverse.
Trovatele anche voi (magari ce ne sono anche altre), ma, mi raccomando… senza usare formule trigonometriche!
Maghi e affini aspettate un paio di giorni... chissà che non si muova un silenzioso inaspettato... grazie!
Le soluzioni sono molteplici, QUI ne trovate alcune






31 commenti
Certo che se una volta, dico una volta , si potesse usare il goniometro....
Comunque, se in un triangolo non sapete quanto valgono due angoli, ( e non vi permettono di misurarne uno) l'unica situazione a vostro favore è che i due angoli siano uguali. Così , conoscendo la loro somma, basta dividere per due! Ma, a occhio, non sembra che il nostro triangolo sia tanto isoscele.
Da qualche parte bisogna ingegnarsi a trovare dei triangoli isosceli, uno , due, insomma, quello che serve, e poi...
Vi sono vari modi per risolvere il problema, disegnando sempre qualcosa in più. In un caso, almeno, basta ricordarsi il secondo criterio di similitudine tra triangoli.
Forza... che i maghi sono pronti ad avventarsi... cercate di arrivarci prima!!!!!!
Ecco, disegnate un paio di righe in più e magari una diagonale, che serve sempre....
Cerea.
L’angolo in B del triangolo ABD è 180-150 = 30°
Due rette perpendicolari ad AD, la prima passante per B, la seconda per C.
La retta passante per AD, e la retta passante per BC.
Risultano due triangoli rettangoli simili, un angolo di 50°, rispettivamente in B il più grande, in C il minore.
Credo di esserci: EBC = 10° e BCE = 60°
Infatti (...):
Si calcolano gli angloli:
ABD = 180° - (80° + 20°) - 50° = 30°
ECD = 180° - (50° + 50°) - 20° = 60°
CEB = AED = 180° - 50° - 20° = 110°
Dal triangolo BCE si ricava che la somma dei due angoli EBC e BCE è uguale a 70° (180° - angolo CEB)
Si tracci la parallela ad AD per C (con F = punto di intersezione con BD e G = punto di intersezione con BA)
Si tracci la parallela a DC per F (con H = punto di intersezione con AD)
Il quadrilatero ECDH è un rombo: per costruzione (angolo CDH = angolo HEC = 100° e angolo FCD = angolo DHE = 80°
Si ha: angolo ECA = 20° (angolo FCD - angolo ECD)
il quadrilatero AGCD è un trapezio regolare (angolo DAG = angolo CDA = 100° e angolo AGC = angolo GCD = 80°) ed i due triangoli di base AD e GC formati dalle sue diagonali sono isosceli
Si ha: angolo DGC = 20° (uguale all'angolo GCA) e angolo GDA = 20° (GC a AD sono parallele per costruzione)
Inoltre il triangolo DGB è isoscele in quanto l'angolo BDG = 30° (50° - angolo GDA) , come l'angolo ADB
La bisettrice dell'angolo DGB interseca la retta BC in I e la retta DC in L e l'angolo CGL risulta pari a 40° (angolo DGB = 120 diviso per 2 (angolo DGL) - angolo DGC (20°)
I triangoli DGL e ACB sono uguali (GD = AC, angolo LDG = angolo BAG e angolo DGL = angolo BCA)
Si ha: triangolo CGI è isoscele quindi BCG = 40° ... e BCE = 60° (40° + GCA)
e quindi ECB = 10° (70° - BCE)
(spiacente: ... non sono riuscito ad allegare il disegno)
che silenzio c'è stasera...
va beh... domani via libera a tutti!!!
Per il terorema della bisettrice applicato agli angoli ADE e EDC
si sa che AD:AE = DC : EC
FG parallela a AC
allora FD:AE=DG:EC
i triangoli FBG a ABC sono simili (secondo criterio)
ECD=CDG=60 (alterni interni)
ECD=CGD=60 (corrispondenti)
nel triangolo FBG gli angoli sono 80+60+30+x=180 cioè x=10
y è 180-60-60= 60
scusate: bastava Talete applicato ai triangoli FBG e ABC
Soluzione 1 arzigogola ottenuta esclusivamente per via geometrica utilizzandoalcune proprietà degli angoli interni dei poligoni:
https://i.imgur.com/TPCd5zo.png
disegno arzigogolo 1-bis senza sottotitoli:
https://i.imgur.com/AeTd1IQ.png
disegno meno arzigogolo sempre senza sottotitoli:
https://i.imgur.com/04Pj1o8.png
Soluzione di Oreste, non molto dissimile da una di quella di Andy. Le vie della geometria non sono infinite...
Un consiglio per Andy : le immagini possono essere inserite direttamente cliccando nel menu in alto sulla penultima icona a destra (quella prima dell' equation editor LATEX).
Ciao Gianfranco . prima di inserire l'immagine la devi pubblicare su un sito (gratuito) come ad esempio postimage... a questo link https://postimages.org/it/
Se vuoi che l'immagine non scompaia dopo qualche mese, ti conviene registrarti, gratis e veloce.
Tu scegli l'immagine da pubblicare, lui la carica nel suo sito e poi ti offre una vasta scelta di utilizzi.
Se opti per la seconda, non fai altro che copiare il link che poi potrai incollare quando apri nel tuo commento la apposita icona delle immagini (penultima a destra), nella apposita finestra.
Spero sia chiaro, se no, chiedi.
Ciao
Spero si vedono gli 80° in basso a destra. Per differenza, nello stesso triangolo andavano segnati i 10° . Ieri i conti tornavano.
caro Leandro,
cercavo di unire le varie soluzioni, ma mi sono accorto che nella tua c'è qualcosa che non torna...
Il punto chiave è quando dici: "ECD=CGD=60 (corrispondenti)".... Non è vero... Mi sa che devi fare un giro più lungo per arrivare a quei 60°...
Hai voglia di sistemarlo?
caro Gianfranco,
dovresti spiegare meglio i vari passaggi... una figura da sola non dice cosa hai trovato prima di qualcos'altro. Il lettore deve seguire l'intero ragionamento...
IL malefico Nobody non sottile: è malevolo.
Angolo AFD=80 quindi ADF è isoscele.
Per il teorema della bisettrice + Talete AD:FD = CD:DG
ma siccome AD=FD allora CD=DG
ma allora CDG è equilatero avendo un angolo di 60 e due lati uguali
caro Andy,
il primo metodo è molto simile a quello di Maurizio, che mi sembra più "compatto". Il secondo dovresti spiegarlo meglio, passaggio per passaggio, così come il primo che mi avevi mandato privatamente...
Cerchiamo sempre di metterci nei panni di chi vede dall'esterno e non sempre riesce a seguire l'ordine delle varie determinazioni...
scusami ancora Leandro, ma...
"Per il teorema della bisettrice + Talete AD:FD = CD:DG"
Teorema della bisettrice applicato a quale triangolo? e poi Talete cosa dice esattamente?
CARI AMICI,
capisco benissimo che per chi risponde ai quiz certi passaggi geometrici sembrino banali. Ne deriva, perciò, che spesso vengano "saltati" dei passaggi che si considerano automatici. Per tanti altri, però, ciò non è vero e crea problemi di comprensione.
Invito, perciò, tutti i risolutori a spiegare sempre tutti i passaggi della loro dimostrazione, cercando di mettersi nei panni di chi non ha la loro esperienza. Le risposte devono essere esplicative per tutti, non solo per me o per i colleghi più esperti. Altrimenti, si perde lo spirito divulgativo che ci deve distinguere.
Non vogliamo dimostrare che sappiamo, ma che siamo capaci di spiegare. A parte che tutti (io per primo) abbiamo sempre tantissimo da imparare...
GRAZIE...
Tracciata la parallela a FG ad AC,
l'angolo AFD=80 (è corrispondente a BAE) .
ECD=60 per la somma degli angoli di ACD.
Segue CDG =60 (alterni interni).
Segue ADF=20.
Segue FAD=80 quindi il triangolo ADF è isoscele,
quindi AD=FD .
Teorema della bisettrice applicato al triangolo ADC (la bisettrice è DE che spicca due angoli uguali di 50):
AD: DC = AE:EC (1)
Invece di Talete utilizziamo il fatto che
ABE è simile a FBD avendo due angoli corrispondenti uguali
ABE=FBD, BAE=BFD
quindi i lati corrispondenti sono in proporzione
AE:FD = BE:BD (2)
idem per i triangoli DBG e EBC ove l'angolo in comune è EBC (incognito)
EC:DG = BE:BD (3)
per la (2) uguagliando si ha
AE:FD =EC:DG cioè
AE:EC=FD:DG
per la (1) allora
AD:DC=FD:DG
ma AD=FD quindi DC=DG
CDG è equilatero e l'angolo DGC = CDG=60
Da cui y=60 perché corrispondente a DGC.
da cui DBG= 180-50-60-60 = 10
bene, bene... grazie Leandro! Come vedi vi erano molti passaggi dentro una singola frase...
Posto il mio secondo disegno con 2 aggiunte.
Traccio la parallela ad AC' che chiamo JK;
traccio la linea h (tratteggiata in rosso) perpendicolare a JK (e ad AC') passante per C:
angolo DCE° = 90° - 60° = 30° => GCO° = DCE° = 30° (angoli opposti al vertice)
il triangolo rettangolo GOC possiede così un angolo GCO° = 30°, il suo complementare OGC° = 90° - 30° = 60°;
GOC è un triangolo rettangolo del tipo "30°, 60°, 90°", che è un particolare triangolo rettangolo dove l'ipotenusa è il doppio del cateto minore;
ovvero GOC è la metà di un triangolo equilatero (CFG) avente per base (FG) il doppio del cateto minore del triangolo rettangolo GOC (FG = 2OG) e per altezza il cateto maggiore (OC) del triangolo rettangolo GOC;
essendo CFG equilatero, l'angolo FCG° = 60°
x° = 180° - C'CF° - GCF° = 180° - 60° - 60° = 60°
y° = 180° - BEC° - 60° = 180° - 110° - 60° = 10°
That's all folks
Scusate, errore di battitura :
:
x° = 180° - C'CG° - GCF° = 180° - 60° - 60° = 60°
grazie Andy... lo inserisco senz'altro...
caro Andy,
stavo controllando la tua soluzione, ma... molte cose non mi tornano (o almeno non mi sono chiare...), Innanzitutto c'è un doppio E e crea confusione. Poi non capisco come tu possa dire" GOC è la metà di un triangolo equilatero (CFG) avente per base (FG) il doppio del cateto minore del triangolo rettangolo GOC (FG = 2OG) e per altezza il cateto maggiore (OC) del triangolo rettangolo GOC". Inoltre, a cosa serve tutta la costruzione a destra?
Forse mi sono perso qualcosa, ma se dai per assodata una prima parte, ti chiederei di mettere tutto assieme...
Grazie...
caro Gianni,
non so come mai, ma il tuo doppio commento era finito negli spam(?)... me ne sono accorto solo oggi...
La tua dimostrazione potrebbe anche essere giusta, ma alcune cose vanno corrette:
HECD non è detto che sia un rombo e potrebbe essere solo un parallelogramma... per come è stato costruito.
Inoltre tu dici che:
I triangoli DGL e ACB sono uguali
e questo non mi torna proprio...
Controlla meglio, anche se penso che il procedimento sia alla fine corretto, anche se può essere accorciato. L'idea del trapezio e delle due parallele è buona, ma cerca di scrivere per bene ogni singolo passaggio...
Provo a completare la dimostrazione che avevo iniziato, di quanto valgono gli angoli EBC ed ECB.
Aggiungo alla mappa una retta parallela ad AD passante per B, e la perpendicolare a BD passante per C che interseca AD nel punto G.
Traccio la retta passante per GE a ottenere il triangolo BFG.
Si calcola prima l’angolo in a di 60°, poi l’angolo in b 40+20= 60°
Si ottiene che il triangolo BFG è con gli angoli di 60°
Osservando l’aquilone BCDG si ottengono gli angoli EBC 10° e ECB 60°.
Si dovrebbe tracciare anche la perpendicolare a BG passante per A e dimostrare che l’angolo di 120° si divide in due 60° e 60°
Per dimostrare che l’angolo di 120° si divide in due, bisogna tracciare anche una linea orizzontale e una verticale nel punto H.
Considerando l’angolo noto in G di 60°, 180-120-30= 30°
Beh... ringraziando Gianni, Giacomo e Andy per i loro sforzi, direi che potremmo concludere il quiz. Chissà quante altre soluzioni ci sono...
