Diamo QUATTRO soluzioni per il quiz geometrico sullo strano quadrilatero confinante con il terreno di Nobody. Se ne arrivassero di nuove le aggiungeremo. Per cui guardate bene il “quattro” iniziale, se diventasse cinque o sei sapreste che c’è qualcosa di nuovo da leggere…

Una veloce premessa. La geometria, anche la più semplice, quella che non fa uso di trigonometria o di funzioni analitiche, sa, comunque, essere ricca di spunti e stimolare la fantasia. Un vero e proprio gioco che si limita alla conoscenza delle relazioni tra angoli e triangoli, basandosi su Talete e poco più. Un campo ideale per esercitarsi anche a livello di scuole medie e per fare amicizia con una materia ben più ricca e vivace di molti giochi da computer...

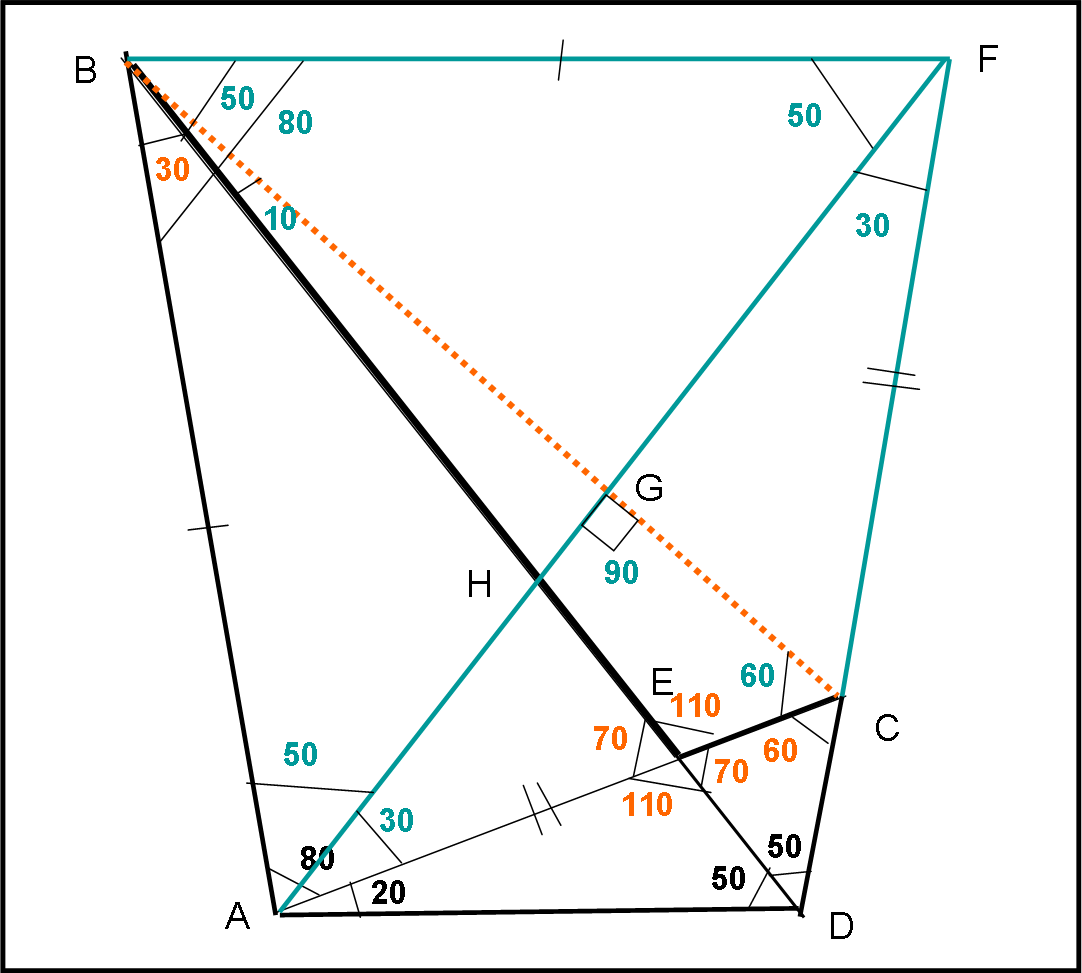
Un avvertimento generale: gli angoli noti fin dall’inizio vengono segnati in nero. Quelli ricavabili immediatamente (opposti al vertice o calcolati come differenza tra 180° e due angoli conosciuti di uno stesso triangolo) sono segnati in rosso. Questa situazione rappresenta quella di partenza e la riportiamo qui di seguito:

In blu sono invece indicati sia i segmenti aggiunti alla figura di base, sia gli angoli ricavati in modo meno immediato..

Iniziamo con la soluzione fornita da Maurizio, in cui fa la sua comparsa una figura geometrica ben conosciuta (almeno una volta…) dai bambini: l’aquilone.

 

Soluzione di Maurizio

La figura da prendere in considerazione è quella che segue. La usiamo per descrivere i vari passaggi.

Dal punto B tracciamo una parallela al lato AD e prolunghiamo il lato DC fino a incontrare la parallela in F. Otteniamo un bellissimo trapezio isoscele AFDA. Che sia isoscele lo si deduce subito dagli angoli in A e in D: entrambi di 1oo°, come indicato nei dati di partenza.

Tracciamo, adesso, la diagonale AF del trapezio. Soffermiamoci un attimo sugli angoli ABF e BFD del trapezio. Essi devono essere uguali tra loro e la loro somma deve essere 360 (somma degli angoli interni del trapezio) meno la somma di BAD e ADF. La somma di questi due è uguale a 200 ° (come appena ricavato)  e quindi la somma di ABF e BFD deve essere di 160°. In altre parole:

ABF = BFD = 80°

Ma sappiamo che l'angolo ABD = 30° e ne segue che:

DBF = ABF - ABD = 80 - 30 = 50°

Attenzione: questo risultato lo potevamo ottenere ancora più velocemente considerando gli angoli DBF e BDA. Essi sono alterni interni di due parallele (BF e AD) tagliate da una trasversale (BD) e, quindi, devono essere uguali. Ma BDA = 50° (dato di partenza) e, di conseguenza abbiamo che

DBF = 50°

Il fatto di avere un trapezio isoscele ci regala un mucchio di informazioni basate sulla sua simmetria. In particolare:

ABD = AFD = 30° (dato di partenza)

BFA = DBF = 50°

Come angoli alterni interni delle solite parallele, tagliate dalla trasversale AF, abbiamo subito che:

BFA = FAD = 50°

Ma

FAC = FAD - CAD = 50 - 20 = 30°

Bene, abbiamo tuttto ciò che ci occorre per analizzare i triangoli  ABF e AFC

ABF ha due angoli di 50° e quindi è isoscele e, in particolare:

AB = BF

ACF ha due angoli di 30° ed è anch'esso isoscele. In particolare:

FC = AC

A questo punto è con grande sagacia che Maurizio introduce l'aquilone. Esso è un quadrilatero con due coppie di lati consecutivi uguali.  (proprio come il classico aquilone dei giochi di una volta...). Nella figura esso è dato da ABFC, dove AC = FC e AB = BF. Notiamo che se tutti i lati fossero uguali l'aquilone diventerebbe un rombo.

A questo punto, basta ricordare una proprietà (facilmente dimostrabile) degli aquiloni: le diagonali sono perpendicolari tra loro.

Il gioco è fatto. Basta analizzare il triangolo AGC. L'angolo in G è retto, l'angolo in A è 30°, da cui segue che:

GCA = 180 - 90 - 30 = 60°

Nel triangolo EGB abbiamo che BEC = 110° e BCE = GCA = 60°

Da cui:

EBC = 180 - 110 - 60 = 10°

Il problema è stato risolto!

E' interessante notare che il trapezio utilizzato ha una caratteristica particolare: tre dei suoi lati sono uguali. Infatti, AB = AF = FD.

Questo metodo, anche se un po' lungo, è quello che preferisco . Innanzitutto, perché fa uso di una figura che vale la pena ricordare (l'aquilone) e inoltre perché usa solo relazioni tra angoli senza utilizzare la similitudine tra triangoli. Un grazie alla solita e ben nota capacità riflessiva di Maurizio e mi scusi se ho preferito usare aquilone invece di deltoide...

 

Soluzione di Leandro

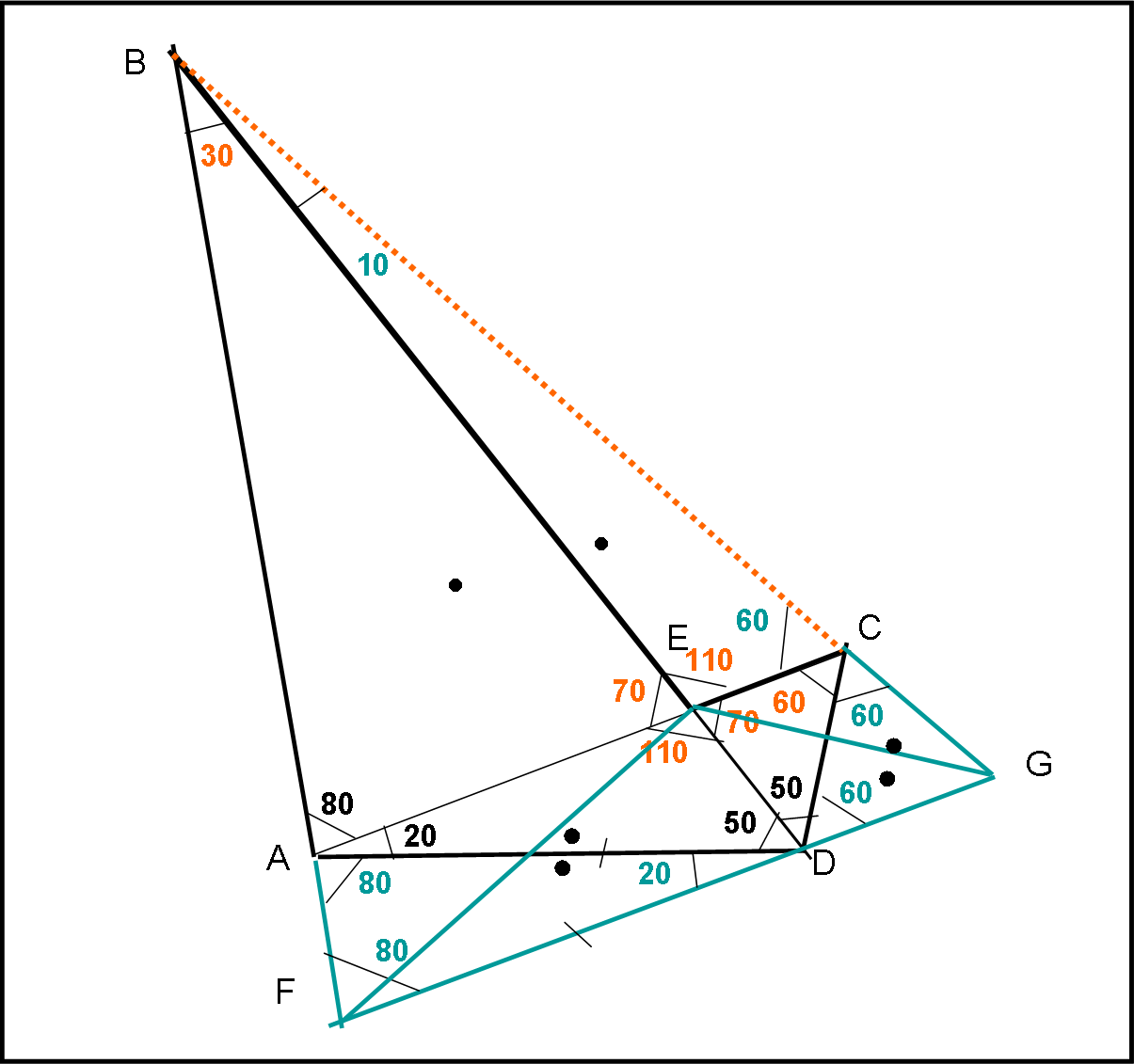
Ovviamente, anche Leandro usa linee aggiuntive (obbligatorio) come mostrato nella figura che segue:

Vengono prolungati i lati AB e AC fino a incontrare la parallela ad AC tracciata da D. Conviene anche unire F e G con E, in modo da evidenziare il triangolo FEG.

Partiamo dal triangolo ACD e , applicando il teorema della bisettrice che abbiamo incontrato da poco (QUI), possiamo scrivere:

EC/EA = CD/DA   .... (1)

La bisettrice considerata (ED) è quella dell'angolo in D, dato che sappiamo fin dall'inizio che i due angoli in cui viene diviso ADC sono entrambi di 50°.

Teniamoci ben stretta la relazione (1).

Consideriamo i triangoli BFD e BAE. Essi sono ovviamente simili, dato che hanno un angolo in comune e gli altri due alterni interni di parallele tagliate dalle trasversali BF e BD.

Possiamo, perciò, scrivere:

AE/FD = BE/BD

Sono però anche simili i triangoli  BEC e BDG, per le stesse ragioni di quelli precedenti. Possiamo perciò scrivere:

BE/BD = EC/DG

Le due relazioni portano all'uguaglianza:

AE/FD = EC/DG

che possiamo anche scrivere:

AE/EC = FD/DG

o ancora:

EC/AE = DG/FD

Ma la (1) ci permette di scrivere:

EC/EA = CD/DA = DG/FD          .... (2)

Fermi tutti! Guardiamo un attimo il triangolo AFD...

L'angolo in A è uguale a 80°, dato che:

FAD = 180 - 80 - 20 = 80°

Ma lo è anche l'angolo  AFD dato che deve essere uguale a BAE = 80°

Il triangolo è isoscele, per cui:

DA = FD

Ma dalla (2) si ha subito che deve essere anche:

CD = DG

Ne segue che il triangolo CDG è anch'esso isoscele. Ma c'è qualcosa di più... L'angolo CDG  vale, infatti:

CDG = 180 - 50 - 50 - ADF

ADF vale 20°, come si può ricavare immediatamente dal triangolo ADF o dall'uguaglianza con  EAD.

Abbiamo quindi che:

CDG = 60°.

Un triangolo isoscele che ha un angolo di 60° deve essere equilatero e quindi anche

DCG = 60°

Basta allora scrivere:

BCE = 180 - 60 - 60 = 60°

e, immediatamente:

EBC = 180 - 110 - 60 = 10°

Il problema è stato elegantemente risolto, affidandosi quasi completamente a Talete.

 

Prima soluzione di Enzo

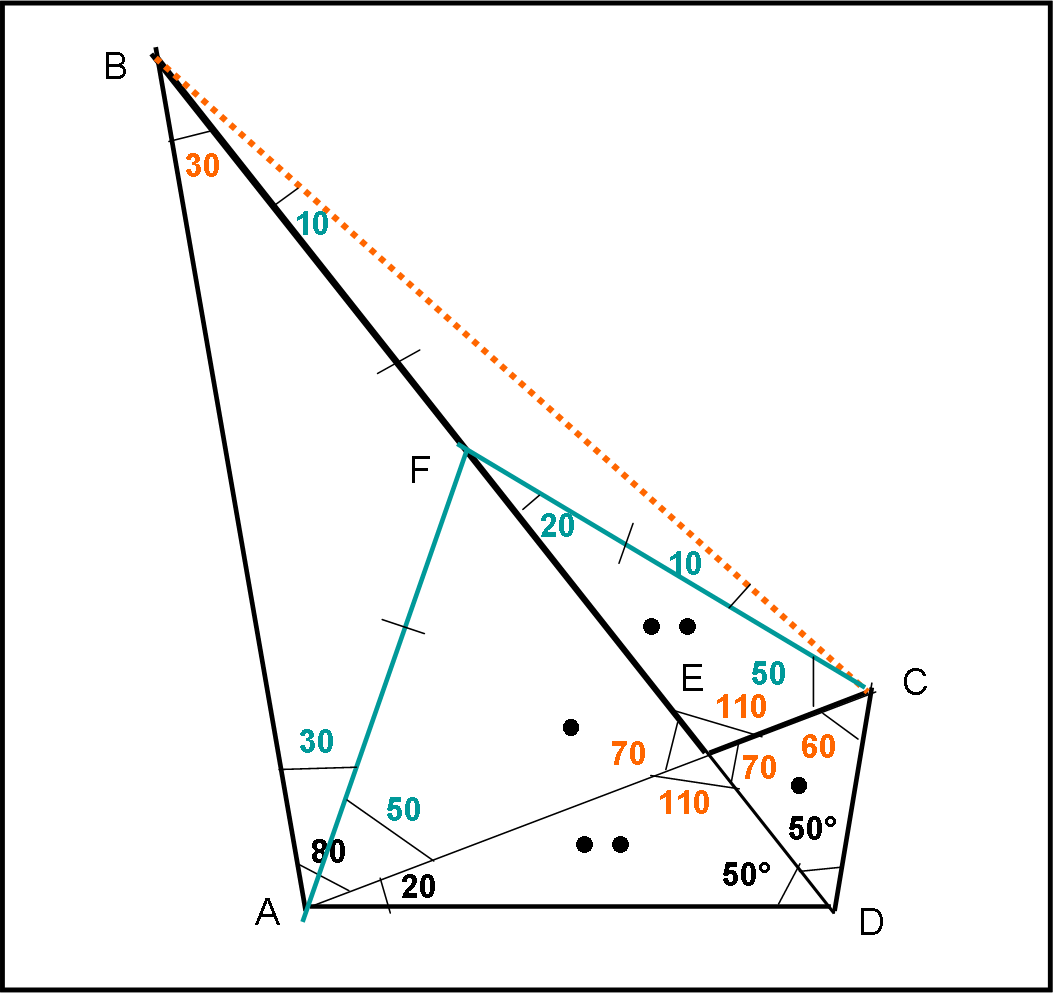
Questa soluzione si avvale dell'aggiunta di due soli segmenti come indicato nella figura che segue:

Tracciamo da A una retta tale da formare un angolo di 30° con AB e la fermiamo nel punto F lungo AE. Congiungiamo, inoltre, il punto F con C.

Il triangolo BFA è per costruzione isoscele, dato che ha due angoli uguali a 30° e, quindi:

BF = FA

L'angolo FAC si calcola facilmente dato che vale:

FAC = BAC - BAF = 80 - 30 = 50°

A questo punto basta notare che i due triangoli AFE e DEC sono simili (due angoli uguali) pr cui vale:

FE/AE = EC/ED

FE/EC = AE/ED

Ma questa relazione ci dice che sono simili anche i triangoli FEC e AED (due lati proporzionali e l'angolo compreso tra loro uguale). Questo fatto ci fa quindi concludere che:

EFC = 20°

FCE = 50°

Ma, allora, il triangolo AFC è isoscele, dato che ha due angoli uguali a 50° (FCE e FAC). Ma se è isoscele vuol dire che

FC = FA

ma, ricordando che FA = BF  si ha:

FC = BF

Ne segue che anche il triangolo BFC è isoscele.

Ma

BFC =  180 - EFC = 180 - 20 = 160°

Si ha perciò che:

FCB = FBC = (180 - 160)/2 = 10°

E, infine:

ECB = FCE + FCB = 50 + 10 = 60°

 

Seconda soluzione di Enzo

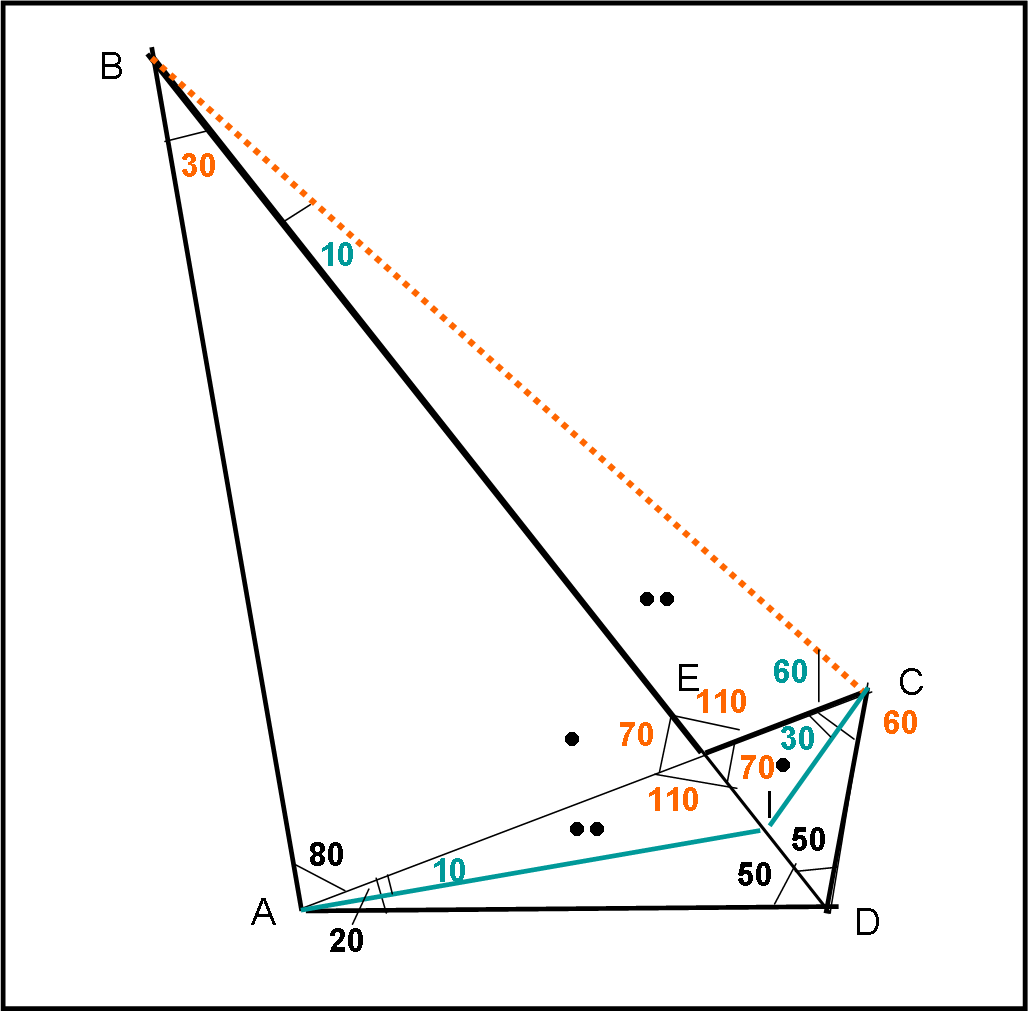
Forse, la soluzione più rapida. Questa volta lavoriamo sulle bisettrici, disegnando quella relativa all'angolo EAD e quella relativa a ECD come ci mostra la figura che segue:

Indichiamo con I l'incentro, ossia il loro punto d'incontro.

I triangoli AEB e CEI sono simili, dato che hanno due angoli uguali

ABE = ECI = 30°

AEB = DEC = 70°

Possiamo scrivere:

BE/EA = EC/EI

BE/EC = EA/EI

Ma, allora sono anche simili i triangoli  AEI e CEB (due lati proporzionali e l'angolo compreso  uguale, BEC = AEI = 110°). Segue, perciò, immediatamente che:

ECB = 60°

EBC = 10°

continua...(?)

Il quiz lo trovate QUI