Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.

Fino all’esaurimento

Ne avevamo già parlato velocemente nel “corso” di matematica (QUI), ma vale la pena riprendere e affrontare la determinazione del pi greco con maggiore attenzione. Se non  altro per cercare di entrare sempre più nella visione geometrica di personaggi geniali come Archimede. Spesso noi dimostriamo le scoperte greche applicando l’algebra e tutto scorre velocemente. Tuttavia, la situazione era ben diversa e i metodi per ottenere un risultato ben più complicati e soggetti anche a limiti di tipo filosofico oltre che pratico.

Un posto di rilievo viene sicuramente occupato dal metodo di esaustione, già noto ben prima di Archimede, ma da lui portato a un livello estremamente rigoroso. La sua prima attuazione si deve ad Eudosso (407-355 a.C.) e viene ripreso da Euclide. Tuttavia, il vero salto di qualità si deve ad Archimede, il quale lo usa solo dopo aver percepito il risultato attraverso il suo metodo meccanico, che già conosciamo bene. Il metodo di esaustione diventa quindi la conferma rigorosa di un procedimento empirico.

Lo stesso “nome” illustra la base del procedimento: esso consiste nel riempire, con figure note sempre più piccole, lo spazio a disposizione fino a che questo venga “esaurito”. In tal modo la somma delle aree delle figure note approssima l’area cercata. Ci rendiamo subito conto che manca ancora un qualcosa a questo procedimento per renderlo praticamente perfetto:  il passaggio al limite (QUI). La tesi finale si dimostrava con un procedimento “per assurdo”. Oggi, sostituiamo il “riempire” e la “dimostrazione per assurdo” con due successioni convergenti e con il calcolo del loro limite comune.

Questo tipo di procedimento illustra molto bene la visione “scientifica” di Archimede: in lui vi è il bisogno di mantenere un’identità tra il mondo geometrico e il mondo fisico; Il metodo meccanico assicura al matematico che il suo ragionamento rispecchi la realtà; il metodo di esaustione serve ad applicare una verità, confortata dalla realtà, al campo quasi mistico e puro della geometria.

Va anche ricordato una specie di blocco mentale che dominava i grandi pensatori dell’epoca e che si rifaceva alle idee aristoteliche sull’infinito. Il concetto era un qualcosa di ben diverso da quello attuale: l’infinito era un qualcosa solo potenzialmente vero, ma mai attuale e attuabile. Una visione quasi “negativa”, basata sull’incompletezza  e su una potenzialità mai realizzabile. Questa sfuggente caratteristica portava al rifiuto di introdurre l’infinito nella matematica greca.

Potremmo lanciarci e dire che Archimede (e non solo lui) avevano colto perfettamente il concetto di limite, ma che l’apparente indefinibilità dell’ infinito matematico lo rendevano un argomento quasi “blasfemo”.

Lo schema della dimostrazione per assurdo è, tuttavia, piuttosto semplice e generalizzabile a qualsiasi  figura curvilinea. Noi l’applichiamo, per maggiore chiarezza, al caso che più c’interessa: la quadratura del cerchio, ossia la proposizione di Archimede:

Ogni cerchio è uguale a un triangolo se ha il raggio uguale all’altezza e la circonferenza uguale alla base.

Sia S_C l’area del cerchio e sia S_T l’area del triangolo.

Si vuole dimostrare che la grandezza S_C è uguale alla grandezza S_T.

Si presuppone, allora, per assurdo, che S_C  > S_T e che la loro differenza sia ɛ.

S_C – S_T = ɛ

Consideriamo la Fig. 39 e inscriviamo un quadrato ABCD nel cerchio e, successivamente, dividiamo gli archi AB, BC, CD e DA  a metà in modo da costruire un poligono con un numero doppio di lati.

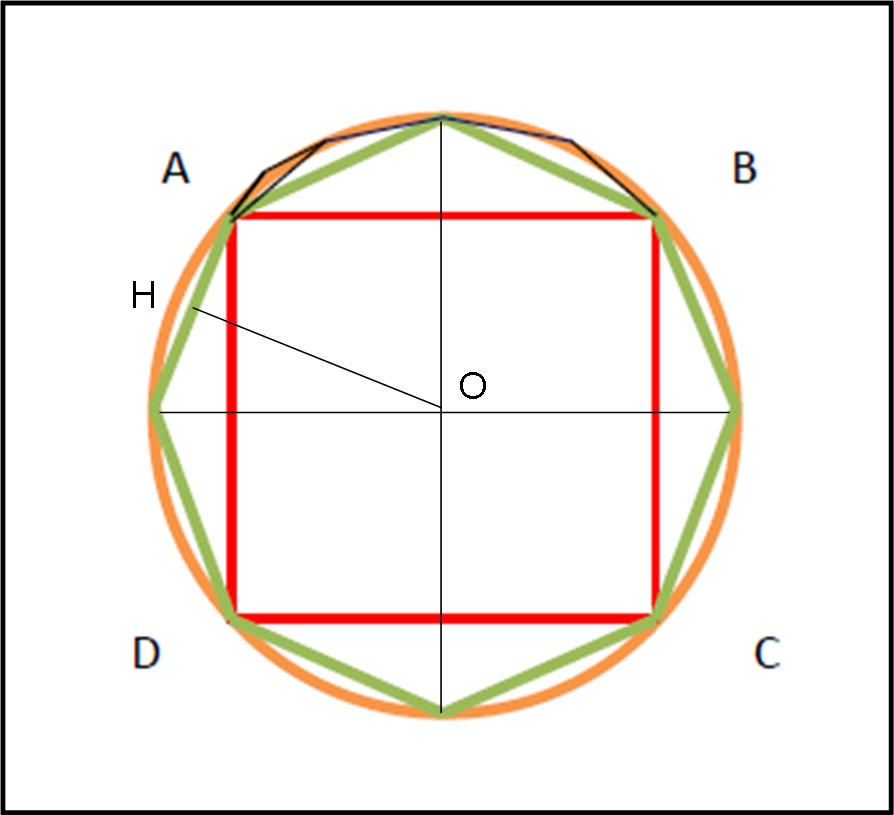
Continuiamo con questo procedimento fino a che la differenza tra l’area del cerchio e quella del poligono S_P sia minore di ɛ.

S_C – S_P < ɛ = S_C – S_T

Il che comporta

S_P > S_T                       …. (1)

Ma S_P è equivalente all’area di un triangolo che ha per base il perimetro del poligono e per altezza l’apotema (OH). Tuttavia, sappiamo per certo che l’apotema deve essere minore del raggio del cerchio e che il perimetro del poligono deve essere minore della circonferenza.

L’area del poligono deve quindi essere minore di quella del triangolo. Ossia:

S_P < S_T

Ma questo è impossibile, essendo contrario alla (1), ossia a quanto è stato dimostrato partendo dall’ipotesi che S_C > S_T.  Deve quindi essere assurda l’ipotesi iniziale S_C > S_T.

In modo analogo si può lavorare con i poligoni circoscritti e dimostrare che è assurda l’ipotesi S_C < S_T.

Ne segue che S_C deve essere uguale a S_T.

Direttamente da questa conferma, Archimede passa automaticamente al calcolo del pi greco, ricordando che la circonferenza c vale 2πr (l’area del cerchio vale ½ c r, ma anche πr², per cui c = 2πr).

Non dobbiamo dimenticare che abbiamo già incontrato la derivazione di Archimede  dell'area del cerchio attraverso il metodo meccanico (QUI).

Ricordiamo ancora che l’uso del simbolo π arriverà molti secoli dopo. Per i greci era solo il coefficiente di proporzionalità che permetteva di scrivere che il rapporto delle aree di due cerchi era uguale al rapporto tra le aree dei due quadrati di lato uguale al raggio, ossia:

S_C1/Sc₂ = r²₁/r²₂

In altre parole, per qualsiasi cerchio Ci :

S_Ci = k r_i²

Dove k è proprio il “nostro” π

Approssimiamo pi greco a fianco di Archimede

L’articolo del corso di matematica è già sufficiente per farsi un’idea del procedimento “pratico”, ma, per chi vuole seguire Archimede fino in fondo, ecco il procedimento completo fino al poligono di 96 lati… Una trattazione apparentemente noiosa, ma che ci permette di avvicinarci di molto al ragionamento effettuato dallo stesso Archimede senza approfittare di scoperte successive. L’unica cosa di diverso sarà ovviamente l’utilizzo di un linguaggio e di simboli “moderni”.

Prima di cominciare, vale la pena ricordare un teorema di Euclide,  usato continuamente nella trattazione, detto delle bisettrici: in ogni triangolo, la bisettrice di un angolo divide il lato opposto in parti proporzionali agli altri due lati.

Dimostriamolo rapidamente…

Consideriamo (Fig. 40) il triangolo qualsiasi ABC.

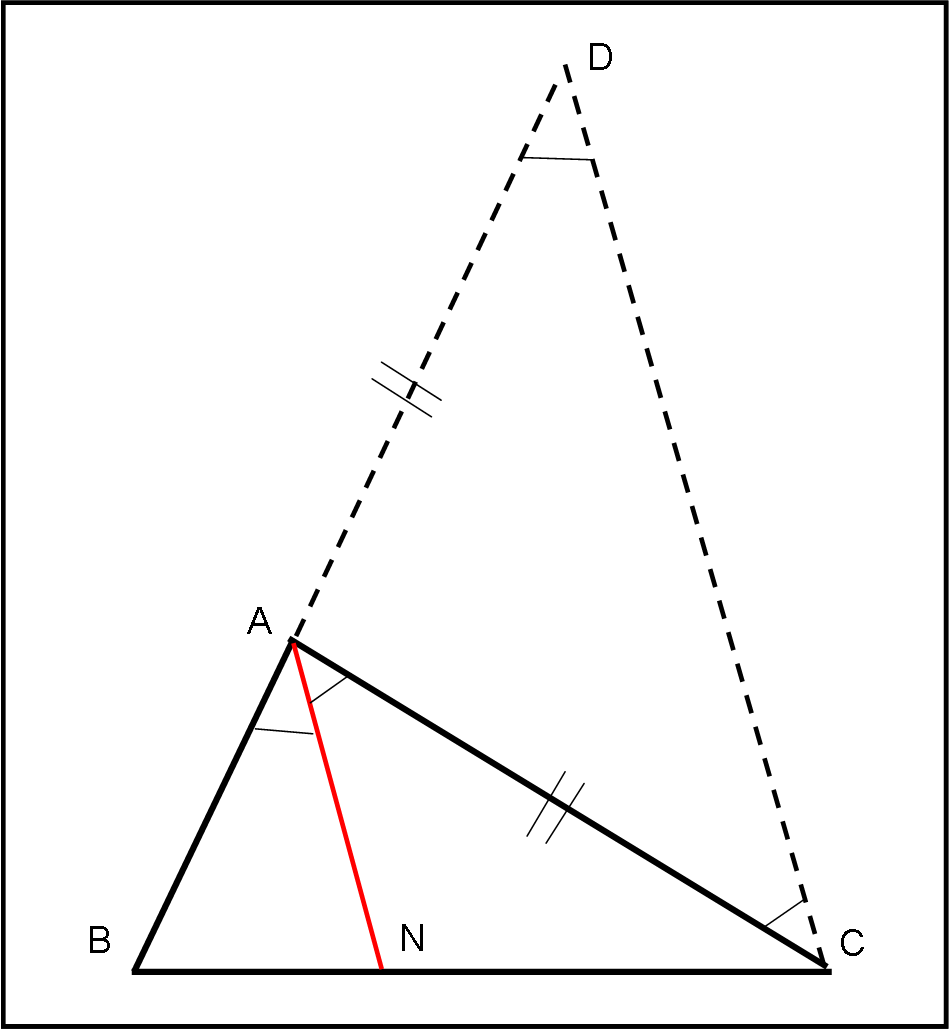
Tracciamo da A la bisettrice che incontra il lato opposto in N. Vogliamo dimostrare che BN/NC = AB/AC. A partire da C disegniamo la parallela alla bisettrice AN, fino a incontrare il prolungamento di AB nel punto D. Consideriamo il triangolo DAC. Abbiamo due rette parallele (BD e AN) tagliate da una trasversale AC. Ne segue che:

NAC = ACD.

Analogamente le due rette parallele sono tagliate dalla trasversale AD, da cui segue che

BAN = ADC

Tuttavia, per definizione di bisettrice, deve essere:

NAC = BAN

E, quindi:

ACD = ADC.

Il triangolo ADC è isoscele e quindi

AD = AC

Per il teorema di Talete si ha:

BA/AD = BN/NC

Ma, AD = AC

Da cui:

BA/AC = BN/NC

c. v. d.

Consideriamo la proposizione di Archimede:

La circonferenza di ogni cerchio è tripla del diametro e lo supera ancora di meno di un settimo del diametro, e di più di dieci settantunesimi

e vediamo di dimostrarla con estrema attenzione e tanta pazienza. Sarà, comunque, una grande esperienza!

Prendiamo un esagono regolare circoscritto a una circonferenza  (Fig. 41 ) e applichiamo subito il teorema delle bisettrici al triangolo ABO, dove AB è la metà del lato dell’esagono Fig. 42).

 

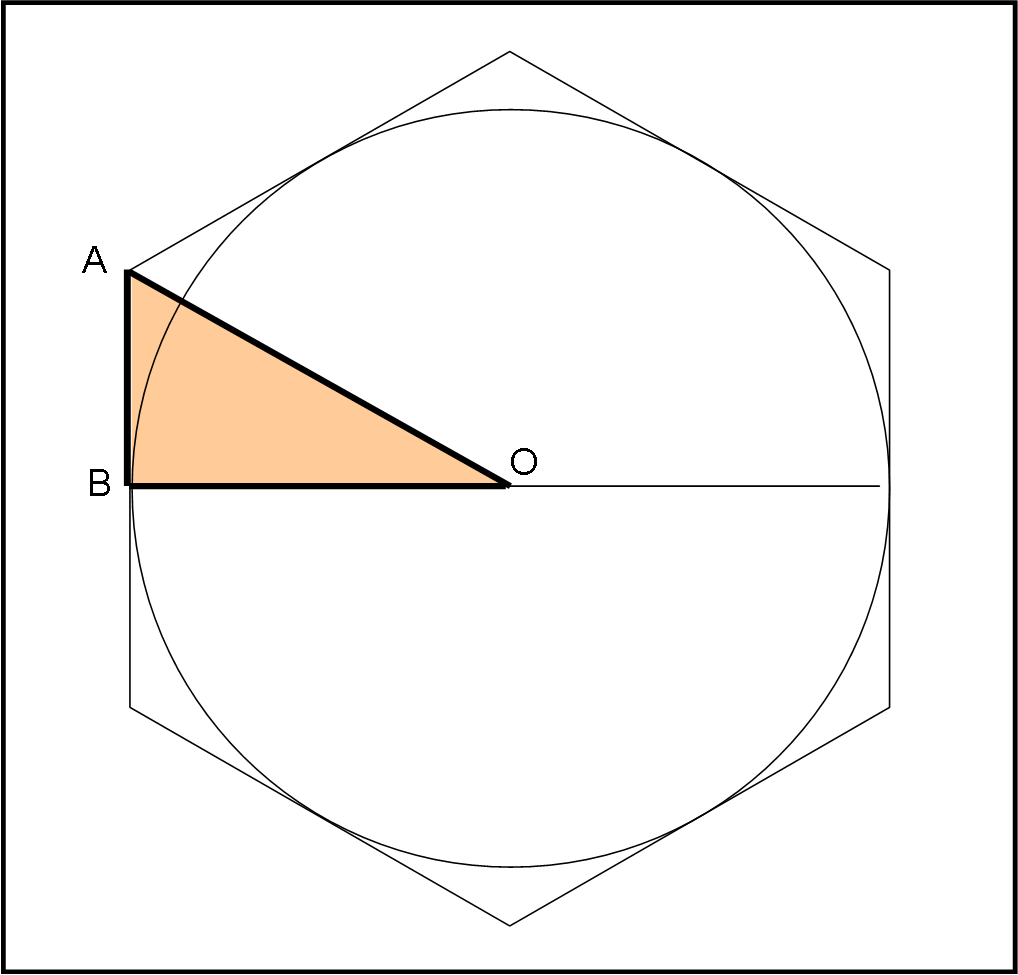
AG/GB = AO/BO

Per la proprietà del comporre:

(AG + GB)/GB = (AO + BO)/BO

AB/GB = (AO + BO)/BO

Invertendo medi con estremi (a/b = c/d;  ad = bc; d/b = c/a)

BO/GB = (AO + BO)/AB

E ancora:

BO/GB = AO/AB + BO/AB         …. (1)

Essendo φ = 30° (proprietà dell’esagono)

AB = ½ AO  (proprietà di un triangolo rettangolo con un angolo di 30°)

Da cui:

AO/AB = 2

Inoltre:

BO/AB = √(AO² – AB²)/AB = √(AO²/AB² – 1) = √(4 – 1) = √3

La (1) diventa:

BO/GB = AO/AB + BO/AB = 2 + √3

A questo punto Archimede deve utilizzare un valore approssimativo per √3 e scrive:

√3 > 265/153

Da cui:

BO/GB = 2 + √3 > 2 + 265/153 = 571/153

In parole povere, possiamo concludere che: il rapporto tra il raggio della circonferenza inscritta r e la metà del lato del dodecagono (s₁₂) è maggiore di 571/153. E’ già qualcosa…

Archimede va oltre e può concludere che deve esistere una relazione simile anche tra la bisettrice OG e il lato del dodecagono. Basta utilizzare il teorema di Pitagora.

GO²/BG² = (GB² + BO²)/BG² = GB²/GB² + BO²/BG² > 1 + (571/153)²

GO/BG > √(349450)/153 > (591 + 1/8)/153

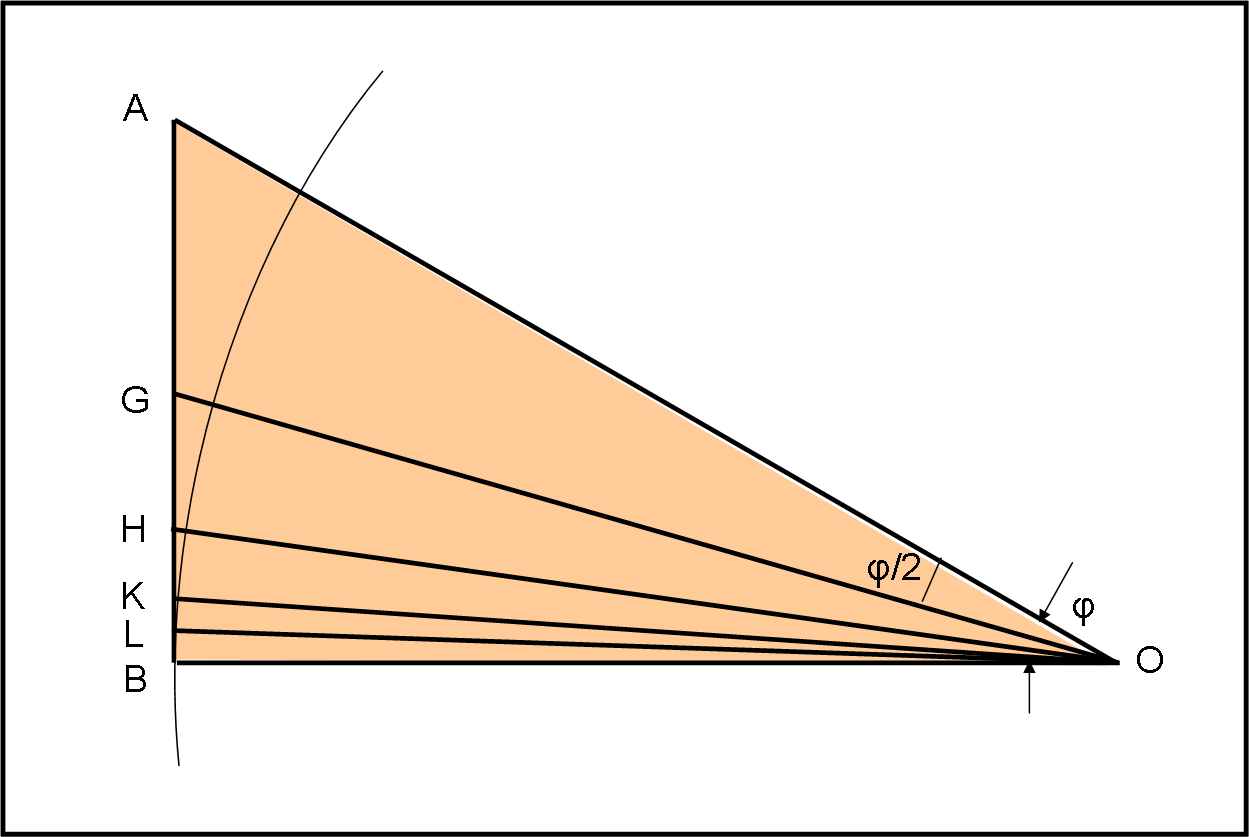
Non resta, adesso, che proseguire, tracciando la bisettrice OH dell’angolo GOB. Ne consegue che BH è la metà del lato di un poligono a 24 lati circoscritto al la circonferenza di partenza.

Applichiamo il solito teorema della bisettrice al triangolo BGO e otteniamo:

GH/HB = OG/OB

Sommando e invertendo medi ed estremi (come fatto nel caso precedente) si ottiene:

BO/HB = (OG + OB)/GB = OG/GB + OB/GB

Ma, da quanto ricavato precedentemente:

OG/GB > (591 + 1/8)/153

OB/GB > 571/153

BO/HB > (591 + 1/8)/153 + 571/153 = (1162 + 1/8)/153

Chiamiamo i segmenti con i loro nomi…

OB = raggio della circonferenza = r

HB = 1/2 lato del poligono a 24 lati = 1/2s₂₄

BO/HB = r/(1/2s₂₄) > (1162 + 1/8)/153

Tracciamo la bisettrice dell’angolo HOB e si determina il semi lato del poligono a 48 lati.

Ripetendo il calcolo precedente si trova facilmente che:

r/(1/2s₄₈) = OB/KB > (2334 + 1/4)/153

Ancora un piccolo sforzo con un’altra bisettrice e si ha:

r/(1/2s₉₆) = OB/LB > (4673 + 1/2)/153               …. (2)

A questo punto Archimede si ferma e costruisce la prima limitazione di pi greco. Seguiamolo con attenzione…

Il primo passo è banale: moltiplicare numeratore e denominatore della (2) per due, in modo da esplicitare il rapporto tra diametro e lato del poligono:

d/s₉₆ > (4673 + 1/2)/153

Non ci resta che moltiplicare il lato del poligono per 96 e abbiamo il suo perimetro p₉₆ :

d/p₉₆ > (4673 + 1/2)/( 96 ·153)

invertiamo numeratore e denominatore ed eseguiamo il prodotto:

p₉₆/d < 14688/(4673 +1/2)        …. (3)

Basta  “pasticciare” un po’ con i numeri, ricordando che i simboli usati oggi non esistevano ai tempi di Archimede e ci si doveva arrangiare in altro modo.

14688 può essere scritto come:

14688 = 3(4673 + ½) + (667 + ½)

Tuttavia:

667 + ½ < 1/7(4673 + ½)

Sostituendo nella (3) si ha:

p₉₆/d < 14688/(4673 +1/2) = (3(4673 + ½) + (667 + ½))/(4673 +1/2) = 3 + (667 + ½)/(4673 +1/2)

E ancora:

p₉₆/d < 3 + (667 + ½)/(4673 +1/2) < 3 + 1/7(4673 + ½)/(4673 +1/2) = 3 + 1/7

Tuttavia, il perimetro di un poligono circoscritto è sempre maggiore della circonferenza iscritta, per cui si può scrivere:

2πr/2r < p₉₆/d < 3 + 1/7

π < 3 + 1/7

che è la prima parte della proposizione di partenza.

Non resta, adesso, che trovare la seconda limitazione…

Il metodo usato non differisce molto da quello che avevamo usato per arrivare all’area della superficie sferica (QUI). Tuttavia, continuiamo seguendo il grande siracusano.

Prendiamo la nostra circonferenza di riferimento e iscriviamo in essa un esagono regolare (Fig. 43)

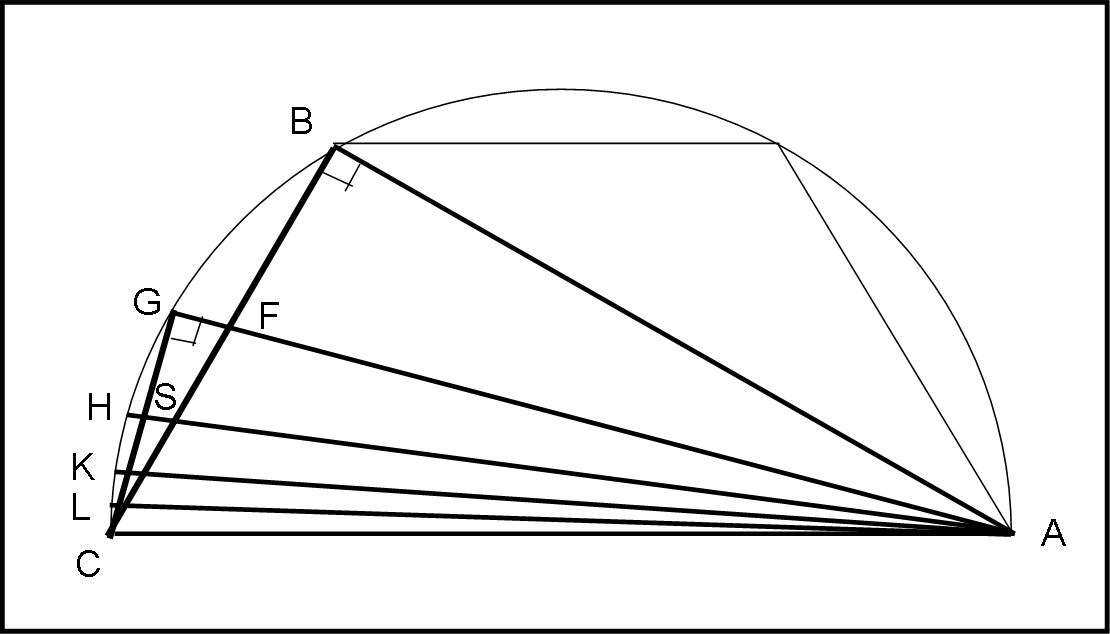
Dato che l’angolo al centro di uno dei suoi lati vale 60°, l’angolo alla circonferenza è, ovviamente, 30°.

Consideriamo il triangolo rettangolo ABC che, avendo un angolo di 30° e uno di 60° comporta

CB = ½ AC

Utilizzando Pitagora si può scrivere:

AB/CB = √((AC²- CB²)/CB²) = √((AC²/CB²) – 1) = √((4 AC²/AC²) – 1) = √(4 – 1) = √3

Archimede sceglie un altro valore approssimato di radice quadrata di tre, ossia:

√3 < 1351/780

Da A tracciamo la bisettrice all’angolo φ = 30°. In tal modo sappiamo che il segmento GB = GC è il lato del dodecagono regolare inscritto nella circonferenza (l’arco GB è uguale all’arco GC).

Particolarmente interessante è il fatto che l’angolo GCB è φ/2, dato che insiste sull’arco GB, lo stesso che sottende l’angolo GAC = φ/2, per costruzione.

Chiamiamo F il punto intersezione tra la bisettrice AG e il lato dell’esagono BC e individuiamo i due triangoli AGC e CGF. Essi sono simili. Infatti, sono rettangoli entrambi e, inoltre, gli angoli in F sono uguali perché opposti al vertice (e CGF = GCB = GAC = GAF per quanto detto precedentemente).

Ne segue che:

AG/GC = GC/GF = AC/CF       …. (4)

Teniamo da parte queste relazioni fondamentali e passiamo al solito teorema della bisettrice che ormai conosciamo molto bene.

BF/CF = AB/AC

Sommando…

(BF + CF)/CF = (AB + AC)/AC

BC/CF = (AB + AC)/AC

Invertendo …

AC/CF = (AB + AC)/BC

Ma dalla similitudine (4) sappiamo che:

AC/CF = AG/GC

Da cui:

AG/GC = (AB + AC)/BC

Ricordiamo, però, che:

AC/BC = 2

e

AB/BC = √3

Da cui:

AG/GC = (AB + AC)/BC = √3 + 2

E ancora (ricordando l’approssimazione per eccesso di √3):

AG/GC < 1351/780 + 2 = 2911/780

In realtà, bisogna trovare (come nella prima limitazione) il rapporto tra diametro della circonferenza e il lato del dodecaedro. Poco male, basta scrivere:

AC²/GC² = (GC² + AG²)/GC² = 1 + AG²/GC² < 1 + (2911/780)² = 9 082 321/(780)²

AC/GC < √(9 082 321/(780)²) < (3013 + 3/4)/780

GC è proprio il lato del dodecagono e AC è proprio il diametro del cerchio, per cui:

d/s₁₂< (3013 + 3/4)/780

Cerchiamo di non “sbuffare” e seguiamo con pazienza Archimede che passa a un poligono di 24 lati, ripetendo l’operazione precedente, utilizzando la bisettrice AH di AGC = φ/2.

Senza certo stupirci troviamo che l’angolo HCG = HAC

Ancora una volta saltano fuori due triangoli rettangoli simili CHS e CHA che portano a scrivere:

AC/CS = AH/CH

Applichiamo senza battere ciglio il teorema della bisettrice al triangolo AGC, con tutti i soliti passaggi:

GS/CS = AG/AC

(GS + CS)/CS = (AG + AC)/AC

GC/CS = (AG + AC)/AC

AC/CS = (AG + AC)/GC

Per la similitudine dei triangoli CHS e CHA, possiamo scrivere:

AH/HC = (AG + AC)/GC

AH/HC = AG/GC + AC/GC

Ma abbiamo da poco trovato che:

AC/GC < (3013 + 3/4)/780

E che:

AG/GC < 2911/780

Ne segue:

AH/CH = AG/GC + AC/GC < 2911/780 + (3013 + 3/4)/780 = 1823/240 (provare per credere!)

Calcoliamo, com’è naturale, il rapporto tra il diametro della circonferenza e il lato del poligono regolare di 24 lati:

AC²/CH² = (AH² + CH²)/CH² = AH²/CH² + 1 < (1823/240)² + 1 = 3 389 299/(240)²

AC/CH < √(3 389 299)/240 < (1838 + 9/11)/240

d/s₂₄ < (1838 + 9/11)/240

Beh… non ci resta che proseguire con la nuova bisettrice AK dell’angolo HAC e dichiarare che il segmento CK è il lato del poligono regolare di 48 lati. Ne segue il solito procedimento che ormai riesce a compiersi quasi da solo. Ci può bastare riportare il risultato che dice:

AC/CK = d/s₄₈ < (1099 + 1/6)/66

Ma potete sempre fare tutti i calcoli come esercizio…

Tracciamo, infine, la nuova bisettrice all’angolo KAC da cui si ottiene il lato del poligono regolare di 96 lati. La conclusione è:

AC/CL = d/s₉₆ < (2017 + ¼)/66

Abbiamo ottenuto il rapporto tra il diametro della circonferenza e il lato del poligono di 96 lati inscritto in essa, seguendo pari pari il procedimento di Archimede; la diseguaglianza non cambia se consideriamo il rapporto tra il diametro e il perimetro della figura (moltiplicando entrambi i denominatori della disuguaglianza sopra scritta per 96, numero dei lati del poligono):

d/(s₉₆·96) = d/p₉₆ < (2017 + ¼)/(96·66) = (2017 + ¼)/6336

Invertiamo numeratore con denominatore e “pasticciamo” un po’ con i numeri:

p₉₆/d > 6336/((2017 + ¼)> (3(2017 + ¼) + 10/71(2017 + ¼))/(2017 + ¼)

p₉₆/d > 3 +10/71

La lunghezza del perimetro di un poligono inscritto è sempre minore della circonferenza, per cui:

2πr/2r = π > 3 +10/71

Che è proprio la seconda parte della proposizione di Archimede…

Unendole insieme, abbiamo, finalmente:

3 +10/71 < π < 3 + 1/7

Sì, può proprio sembrare che Archimede abbia dato i … numeri, ma la conclusione è un risultato fondamentale, dato che stabilisce due cifre decimali al nostro pi greco:

3.140845 < π <  3.142857

Non chiediamoci nemmeno perché Archimede non sia andato oltre con i poligoni… per guadagnare una cifra decimale doveva aumentare di molto il numero di lati. Resta il fatto che seguendo quasi con “paranoia” tutta la trattazione del genio siracusano abbiamo ottenuto due risultati molto importanti, su cui invito a riflettere:

1) Pur nella lunghezza e monotonia della dimostrazione abbiamo usato un metodo alla portata di qualsiasi ragazzino delle scuole medie. Un bell’esercizio che ha come scopo non un qualsiasi risultato predisposto, ma nientemeno che la prima stima oltremodo accurata (in un certo senso) di uno dei numeri più importanti per l’essere umano e sicuramente per l’Universo stesso. Un numero che nasconde ancora oggi misteri insoluti e che deve essere patrimonio di tutte le menti senzienti.

2) Seguendo in modo così semplice e banale il ragionamento di Archimede ci si immedesima nella mente prodigiosa di uno dei più grandi pensatori della storia umana. Indipendentemente dai numeri che scorrono sotto le nostre dita (e che potrebbero essere solo dei sassolini o dei segni) si riesce  a percepire la grandezza dell’impostazione generale e la costruzione di un’opera d’arte impregnata di intuizioni e di fantasia. Un gran bell’esercizio per qualsiasi mente odierna.

No, non mi pento di avervi annoiato e spero proprio che pochi saltino questa apparentemente inutile dimostrazione: è alla portata di tutti e regala una profonda riflessione sulle complesse semplicità del nostro cervello. In fondo… basta aprire il celebre paracadute!

 

QUI gli altri articoli dedicati alla storia infinita del pi greco

***********************************************************************************************************************

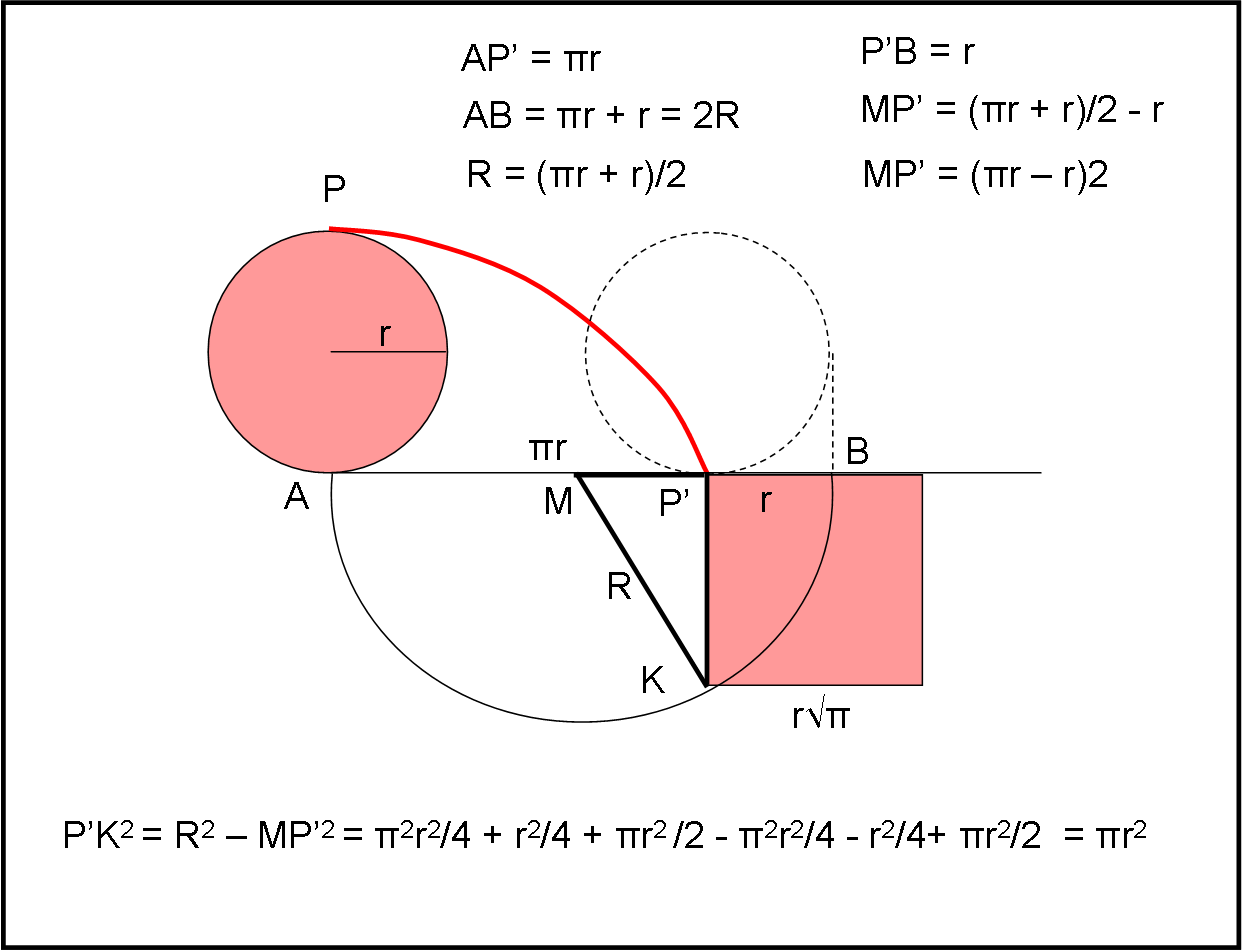
Appendice … risolutiva

Avevamo proposto (QUI, nei commenti) di utilizzare la ormai celeberrima cicloide per quadrare un cerchio, Bene, approfittiamo della illustre presenza di Archimede (che, però, non conosceva ancora quella meravigliosa curva), per dare la soluzione. Basta studiare per bene la figura che segue (mezza cicloide è rappresentata dalla curva rossa) e tutto risulta chiaro…

Appendice… interrogativa

Dimostrare, con mezzi moderni, che il metodo di esaustione funziona perfettamente per il numero di lati che tende a infinito. In altre parole, dimostrare che sia il perimetro dei poligoni regolari circoscritti che di quelli inscritti in una circonferenza tende a 2πr per il numero di lati che tende a infinito.

Buon lavoro!

 

QUI gli altri articoli dedicati all'infinita storia del pi greco