Categorie: Matematica
Tags: Archimede area del cerchio circonferenza pi greco sommatoria
Scritto da: Vincenzo Zappalà
Commenti:12
41. Archimede e l’esaustione **
Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"
Potevamo iniziare subito con il calcolo dell’area definita da una funzione qualsiasi (e non solo da una retta come fatto finora utilizzando spazio, velocità e accelerazione). Tuttavia, prima di far ciò, è più che doveroso richiamare i metodi che hanno portato Archimede a ricavare il valore di pi greco e dell’area del cerchio. Due problemi che hanno accompagnato l’uomo per tutta la sua storia e che hanno visto le “sommatorie” come attori fondamentali. Il lavoro di Archimede ha, in pratica, iniziato la storia degli integrali.
Il problema del calcolo delle aree di figure geometriche ha sempre avuto un’importanza fondamentale fin dai tempi più antichi. In particolare, il risultato forse più celebre è quello ottenuto da Archimede per l’area del cerchio. Lo descriviamo accuratamente, in modo tale che si capisca subito come il calcolo di un’area di una figura qualsiasi si riconduca all’esecuzione di una somma delle aree di poligoni semplici, come il triangolo o il rettangolo.
Possiamo dire, senza paura di smentite, che proprio gli approcci di Archimede hanno dato il via al calcolo dell’integrale di una funzione, sviluppato poi nel 1600 e 1700. E’ quindi doveroso richiamare il risultato, molto grezzo ma illuminante, di una tra le menti matematiche più grandi della storia dell’uomo.
Il problema che si poneva Archimede era quello della cosiddetta quadratura del cerchio, che ormai sappiamo essere insolubile. In poche parole, si voleva disegnare un quadrato che avesse come area quella di un cerchio, con l’utilizzo di una riga e di un compasso. Per ottenere ciò sarebbe necessario disegnare un quadrato di lato rπ1/2 dato che la sua area diventerebbe proprio r2π , pari a quella di un cerchio di raggio r, come mostrato in Fig. 1.
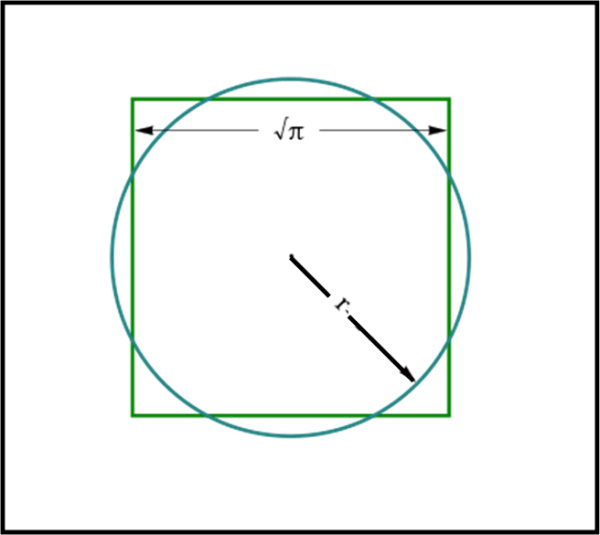
Il che equivarrebbe a riuscire a tracciare un “qualcosa” di lunghezza π. Purtroppo, il numero π è un numero trascendente, ossia non algebrico, e non può essere “costruito” (la dimostrazione non è cosa facile ed è stata ottenuta solo a fine ‘800). Tuttavia, ciò non toglie, che un risultato “perfetto” (che, in realtà, già gli antichi pensavano non ottenibile) possa essere approssimato sempre meglio. Archimede è stato il vero iniziatore di questa storia matematica lunghissima.
Cominciamo con un doppio “avvicinamento”. Archimede considera un poligono interno e uno esterno al cerchio di raggio r, come mostrato in Fig. 2.
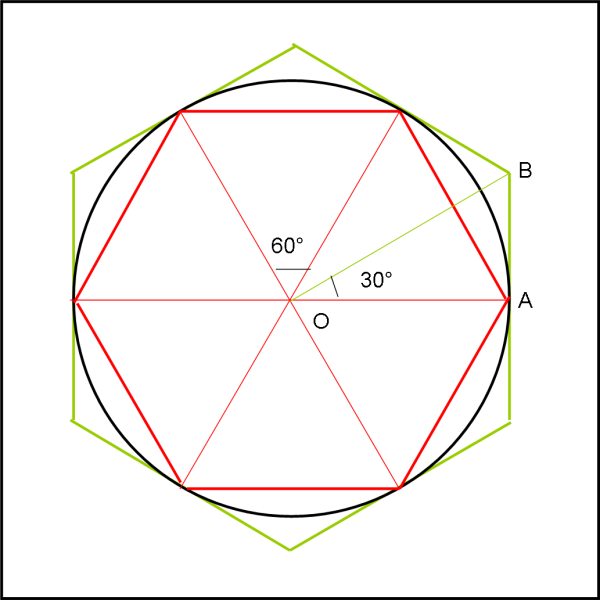
All’inizio, costruisce un esagono interno e uno esterno alla circonferenza. Quello iscritto è formato da sei triangoli equilateri dato che gli angoli devono essere di 60°. I lati di questi triangoli sono uguali al raggio r per costruzione. Il perimetro dell’esagono risulta essere
pi = 6r.
Consideriamo, adesso, l’esagono esterno alla circonferenza, i cui lati sono ad essa tangenti. Ne segue che OAB è un triangolo rettangolo, dato che OA deve essere perpendicolare ad AB. Per costruzione l’angolo AOB è di 30°. Utilizziamo un po’ di trigonometria banale e la definizione di tangente:
BA/OA = tan (30°)
BA = OA tan (30°)
Ma
tan (30°) = √3/3
e, quindi:
BA = OA √3/3
Tuttavia, risulta anche che:
OA = r
E, infine:
BA = r √3/3
Per avere il perimetro dell’esagono circoscritto alla circonferenza basta moltiplicare BA per 12, ossia:
pc = r 12 √3/3 = 4 r √3 = 6.9282 r
La lunghezza della circonferenza c deve, allora, essere compresa tra il perimetro dei due esagoni, ossia:
6r < c < 6.9282 r
Definendo π come rapporto tra cinconferenza e diametro del cerchio si ha:
π = c/2r
Ossia:
c = π 2r
e, ancora:
6r < π 2r < 6.9282 r
Dividendo tutto per 2r, si ha, infine:
3 < π < 3.4641
Un’approssimazione non certo molto precisa… ma basta passare ai dodecagoni, uno inscritto e uno circoscritto, per ottenere (tralascio i passaggi trigonometrici):
3.106 < π < 3.215
Già molto meglio… ma si può, abbastanza facilmente, proseguire. Archimede arrivò a questo risultato:
3.140845 < π < 3.142857
In poche parole, determinò con esattezza le prime due cifre decimali. Vi sembra poco per quei tempi? Era più che sufficiente per disegnare un quadrato che avesse un’area molto simile a quella del cerchio.
Il sistema del poligono interno ed esterno, porta facilmente a un metodo che i limiti sarebbero capaci di rendere ben più interessante. Non ci vuole molto a dire che:
lim n→∞ pi = lim n→∞ pc = c
Il perimetro del cerchio è uguale al limite (comune), per n che tende a infinito, dove n è il numero dei lati dei poligoni. Analoga conclusione si può avere per l’area del cerchio, considerando i limiti dell’area del poligono interno e di quella del poligono esterno.
Onore, comunque, al sommo Archimede, il quale, oltretutto, calcolò l’area del cerchio anche in un altro modo, attraverso l’esaustione. Anche se non enunciato espressamente, egli pose le basi del limite di una successione e di concetto di integrale.
Archimede considerò solo triangoli interni al cerchio. In particolare, ideò la Fig. 3.
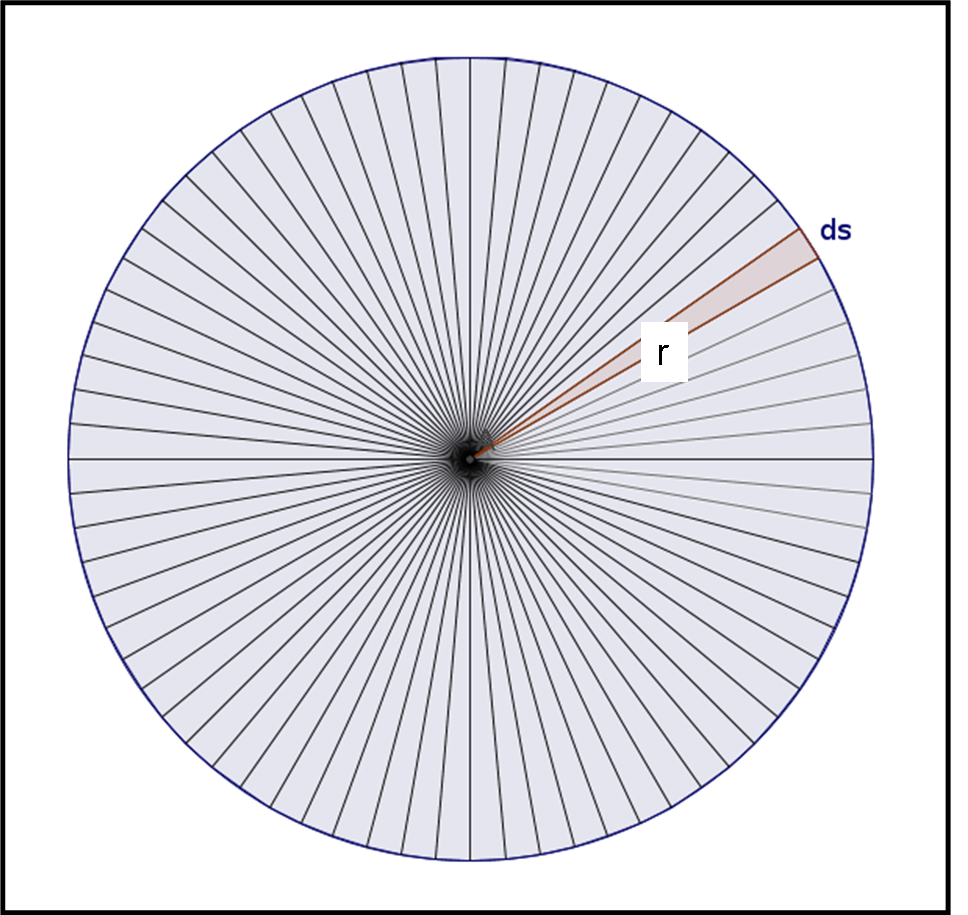
I triangolini considerati da Archimede hanno per base un arco di cerchio, talmente piccolo, però, che può essere considerato lineare. Chiamiamolo ds. L’altezza del triangolo è sempre il raggio r del cerchio. L’area è quindi:
dA = r ds/2
L’area del cerchio non è altro che la somma di tutti questi triangoli, ossia:
A = Σ r ds/2 …. (1)
Dove il numero dei triangoli usati nella sommatoria può essere grande a piacere (teoricamente infinito…).
R e 2 sono costanti e possono essere portati fuori dalla sommatoria; si ottiene:
A = (r/2)Σds …. (2)
Ma la somma di tutti gli archetti ds non è altro che la circonferenza, ossia 2πr,e , quindi:
A = r ·2πr/2
Questa espressione ci dice una cosa importantissima (un celebre enunciato di Archimede): L’area di un cerchio è equivalente a quella di un triangolo rettangolo che abbia per cateti il raggio (r) e la circonferenza (2πr). Un enunciato straordinario, anche se il triangolo non potrebbe comunque essere disegnato a causa della trascendenza di π, a meno che non ci si accontenti di una approssimazione anche molto elevata. Fisicamente è, quindi, possibile, mentre matematicamente no…
La formula precedente diventa, dopo le semplificazioni, la formula ben nota a tutti:
A = πr2
Bene, prima di concludere questo articolo, non solo omaggio ad Archimede, ma anche alle vere basi del calcolo integrale, è bene notare la formula (1) o (2)
Quel segno di sommatoria, quando il numero dei termini va a infinito ci porta esattamente all’integrale… non per niente il suo simbolo è proprio la S di sommatoria. Ma, fermiamoci qui e dalla prossima volta iniziamo a seguire un discorso più organico e continuo.
Questo pi greco non finirà mai di stupirci... se vi sembra impossibile che possa riservare altre sorprese, leggete QUI e QUI ![]()
QUI, invece, gli articoli dedicati alla storia infinita del pi greco
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






12 commenti
Rieccomi qui!
Caro Enzo, vedo che con la matematica stai filando come un treno (.... ovviamente non italiano ).
).
Come ben sai la cosmologia è per me come il prezzemolo: sta bene dappertutto!
... e allora mi è venuto fatto di pensare che la curva del cono di luce (distanza in funzione del tempo) ammette un massimo relativo ... beh, perchè non calcolarlo?
Ho proceduto in questo modo:
1. Ho considerato un universo "piatto" fin dall'origine dei tempi, per avere formule certe su cui lavorare;
2. In detto caso sappiamo che a(t)=(t/T)^2/3, dove t è l'istante dell'emissione e T l'istante dell'osservazione di tale emissione;
3. a(t)=Df/Dc, dove Df è la distanza all'istante dell'emissione mentre Dc è la distanza all'atto dell'osservazione.
4. Dc=∫(c*dt/a(t), da integrare tra t e T.
Mettendo insieme le informazioni suddette si ottiene la formula che fornisce Df in funzione del tempo t. Se ne fa la derivata e si calcola il valore di t per cui detta derivata si annulla. C'è da risolvere un semplice integrale ed una semplice derivata.
Naturalmente bisogna fissare un valore per T. Ad oggi sappiamo che T=T0=13,8 mld-anni, ma possiamo fissare qualunque valore di T e disegnare un grafico in cui si vede come varia la posizione del massimo in funzione del valore di T fissato.
Tutti i massimi così disegnati, se non sbaglio, sono punti appartenenti alla sfera di Hubble che rappresenta il luogo dei punti in cui la velocità di recessione è pari a c.
Alla fine della giostra ho ottenuto quanto segue:
- t = (8/27)*T
- Df = (4/9)*T
- Dc = T
- a = (4/9)
Quindi, se T=T0=13,8:
- t = 4,088
- Df = 6,13
- Dc = 13,8
La cosa interessante è che il massimo si presenta sempre quando il fattore di scala a(t) ha il valore di 4/9.
Ho scritto eresie ... cosmiche?


vedi caro Alvy, contano poco le eresie o le non-eresie. Ciò che conta è che tu hai introdotto vari concetti senza spiegarne i passaggi. Hai anche introdotto un integrale, cosa che stiamo per spiegare in matematica. Ti chiedo allora, se vuoi veramente dare un contributo efficace per tutti e non per pochi, di spiegare passo a passo ciò che hai fatto, senza però pretendere di dare un risultato per un integrale che teoricamente nessuno sa ancora fare ...
Vedi, come già ben sai e come altri mi hanno già chiesto di fare, questo circolo non vuole essere un forum in cui di discute di tutto e di più, a casaccio, passando dal periodo sinodico alla teoria delle stringhe. Io vorrei dare un quadro continuo e logico alla portata di tutti. D'altra parte, avrei potuto introdurre benissimo la dinamica relativistica anche senza spiegare gli integrali e le serie, ma mi sarebbe sembrato poco onesto per chi vuole cercare di cogliere il quadro d'insieme e non ha ancora le basi fondamentali.
Ogni tanto parlo di news più complicate, ma cerco sempre di mantenere il discorso a livello qualitativo. per passare a quello quantitativo sono necessarie le basi se no il circolo rischia di diventare qualcosa di "elite" e ciò non va assolutamente bene.
Insomma, il discorso che hai proposto può essere interessante e istruttivo, ma dovresti dare tutto come sconosciuto e aspettare che tutti abbiano la possibilità di sapere cosa rappresenta un integrale...
Tu hai anche mille ragioni di voler andare più in fretta, ma io devo barcamenarmi e far contento il numero più alto di lettori. Soprattutto gettare basi solide per gli studi futuri che ciascuno vorrà (o non vorrà) poi compiere in modo autonomo.
Capito mi hai????

Hai ragione Enzo, ho sbagliato l'approccio. In realtà non ho voluto dare i passaggi intermedi proprio per evitare di sproloquiare su argomenti che stai cominciando ad affrontare. Diciamo che ho avuto il torto di inserire un dialogo "inter nos" anzichè rivolgermi a tutto il circolo; il fatto è - ed in tal senso ti chiedo comprensione - che ho pochissimo tempo da dedicare al nostro amato circolo e sono costretto, mio malgrado, ad inventare scorciatoie. Mi preme sottolineare che non mi interessa dimostrare quanto sono bravo (o somaro?!?!) ma solo arrivare ad avere una tua risposta in tempi brevi.
(o somaro?!?!) ma solo arrivare ad avere una tua risposta in tempi brevi.
Va beh, facciamo così, indico il percorso che ho seguito per arrivare alle conclusioni che ho riportato sopra.
Cominciamo.
La distanza comovente Dcom è, per definizione, la distanza fisica di un oggetto ad oggi (T0=13,8), vale a dire al tempo dell'osservazione; d'altra parte, al tempo t dell'emissione, l'oggetto distava Df.
Sappiamo che il fattore di scala dell'universo vale a(t) = Df/Dcom per un dato oggetto: l'altro oggetto, quello cioè rispetto al quale si valuta la distanza, siamo ... noi!
Chiamo Dc la distanza fisica di un oggetto al tempo T (tempo di osservazione). In generale T sarà diverso da T0.
Similmente alla Dcom, definisco Dc come ∫(c*dt/a(t), da integrare tra t e T.
So anche che a(t) = (t/T)^2/3 e che Df=Dc*a(t).
Sostituendo, ottengo: Df = a(t)*∫(c*dt/a(t) = [(t/T)^2/3]*∫[(T/t)^2/3]*dt,
avendo posto c=1.
Ancora: Df = [(t/T)^2/3]*[(T^2/3)*3*(t^1/3)] = 3*t^(2/3)*(T^1/3-t^1/3)
Infine: Df = 3*(t^2/3)*(T^1/3)-3*t
La derivata di Df rispetto al tempo vale: 3*(T^1/3)*(2/3)*(t^-1/3)-3
Il massimo si ottiene uguagliando a 0 la derivata, ovvero:
t = ((2/3)*(T^1/3)^3 = (8/27)*T.
Sostituendo si ottiene il valore di Df: Df = (4/9)*T
Il resto viene di conseguenza.
Ora posso fissare un qualunque valore di T, maggiore o minore di T0, per ricavare t e Df.
Scusate di nuovo il maldestro approccio.
No, caro Alvy... non ci siamo proprio. Abbi pazienza, ma non abbiamo ancora concluso con la RR e tu già parli di fattori di scala e dai come cosa stranoto il calcolo di un integrale. Non voglio assolutamente estendere questa discussione nel circolo. Sarà affrontato il problema a tempo debito... In ogni modo ti allego un link molto buono dell'Università di Milano che affronta le basi della cosmologia in modo piuttosto semplice. Semplice, ma ancora non per tutti, di certo...
Lì troverai le soluzioni ai tuoi dubbi ...
http://cosmo.fisica.unimi.it/assets/IntroAstro/IntroAstro1011/lezione5.pdf
Sto cercando di portare gli integrali (uno spauracchio per tanti liceali e non solo) alla portata di chiunque abbia voglia di pensare e di ragionare e non posso proprio saltare ai problemi cosmologici, per semplici che siano. Una cosa è parlare di espansione e di tante belle cose, un'altra è descrivere quantitativamente la cosmologia.
Abbi pazienza e non picchiarmi!
No Enzo, anzi ti ringrazio.
Solo una nota Enzo e poi chiudo con l'argomento.
So perfettamente che il fattore di scala EFFETTIVO non è quello che ho semplicemente esposto. Il mio voleva solo essere un esercizio applicato ad un ipotetico universo il cui fattore di scala fosse quello da me riportato. Tutto qui.
Grazie a te Alvy e sono sicuro che mi capisci. Sì, sì, la scelta di un fattore di scala più o meno veritiero è solo un modo per avere un dato. Come vedrai, il discorso fila abbastanza...
Caro Enzo, ho provato a stimare il valore di pi greco, usando due poligoni (uno interno ed uno esterno) di 24 lati.
Quello che mi sembra è che il problema sia quello di trovare il rapporto tra il lato del poligono esterno o il lato del poligono interno ed il raggio...
Per trovare questo rapporto ho usato il sistema da te descritto per l'esagono esterno (la tangente dell'angolo α), mentre per il poligono interno ho usato il seno dell'angolo α, sfruttando il fatto che si ha a che fare con triangoli isosceli (due lati sono uguali al raggio) e che questi sono “separabili” in due triangoli rettangoli.
http://www.astrobin.com/full/225997/F/
Il valore dell'angolo α è dato da 360°/2 x(numero dei lati del poligono), ossia 360°/48=7,5°.
Usando questo metodo la stima si può affinare..
Per esempio usando poligoni di 1800 lati, si ottiene un angolo
α = 360°/2 (1800)= 360°/3600 = 0,1°
Tang (α) = 0,001745331
Perimetro esterno = 3600 r 0,001745331 = 6,28319168
sin (α) = 0,0017453283
Perimetro Interno = 3600 r 0,001745331 = 6,28318211
Stima valore π
6,28319168 r < π 2r < 6,28318211 r diviso 2r
3,1415910 < π < 3,1415958
Mi sembra che funzioni, o sbaglio?
Paolo
caro Paolo,
sei meglio di Archimede!!!!
Seeee .... Archimede era un genio e non usava la calcolatrice per trovare seno e tangente…
Tra l’altro, nell'ultima formuletta riportata c’è un refuso (giusto per non farsi mancare niente ), dato che anche se il calcolo del Perimetro Interno è corretto, per la fretta ho inserito nell'operazione matematica il valore di tang (α) invece di sin (α).
), dato che anche se il calcolo del Perimetro Interno è corretto, per la fretta ho inserito nell'operazione matematica il valore di tang (α) invece di sin (α).
Volendo il metodo trovato può essere compattato in una semplice formuletta:
α = 360°/2n dove n è il numero dei lati del poligono esterno e/o di quello interno;
P (est) = Tang (α) 2n r
P (est)/2r = Tang (α) n
P (int) = sin (α) 2n r
P (int)/2r = sin (α) n
sin (α) n Tang (α) n
o anche:
sin (360°/2n) n Tang (360°/2n) n
E’ del tutto evidente che affinché sin (α) = Tang (α), l’angolo α dovrebbe ridursi a zero e di conseguenza n = ∞ (360°/ ∞ = 0°)…..
Ne segue che se n tende a infinito, l’angolo α tende a zero per cui più è alto il numero di lati dei poligoni utilizzati, più la stima del valore di π può essere approssimata con precisione.
Paolo
Non capisco perché sono scomparsi i simboli di maggiore, minore e pi greco.
Riprovo:
sin (α) n < π < Tang (α) n
o anche:
sin (360°/2n) n < π < Tang (360°/2n) n
Paolo
perfetto Paolo,
la differenza tra seno e tangente tende ad annullarsi proprio al tendere dell'angolo a zero o, se preferisci, al diminuire dell'archetto di circonferenza. Non per niente, quando si tratta con angoli piccoli come nella parallasse, è del tutto arbitrario usare il seno, la tangente o lo stesso angolo espresso in radianti.