Quasi-QUIZ: di rettangolo in rettangolo… ***

16/03/18

Quasi-QUIZ: di rettangolo in rettangolo… ***

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:16

Questo articolo è inserito come “quiz” solo perché la prima parte è alla portata di molti e può già far capire a cosa si sta mirando. In realtà, il risultato si ottiene in modi diversi, ma questo metodo puramente geometrico (o quasi) mi è sembrato un ottimo e poco conosciuto approccio. Poi potremo andare più a fondo (e Umberto ci aiuterà senz’altro…) e fare una piccola celebrazione.

Valutando l’inizio di questo divertente gioco geometrico, sembra quasi impossibile che si arrivi a un risultato che sembrerebbe del tutto fuori tema. E, invece…

Costruiamo una serie di rettangoli in modo estremamente semplice.

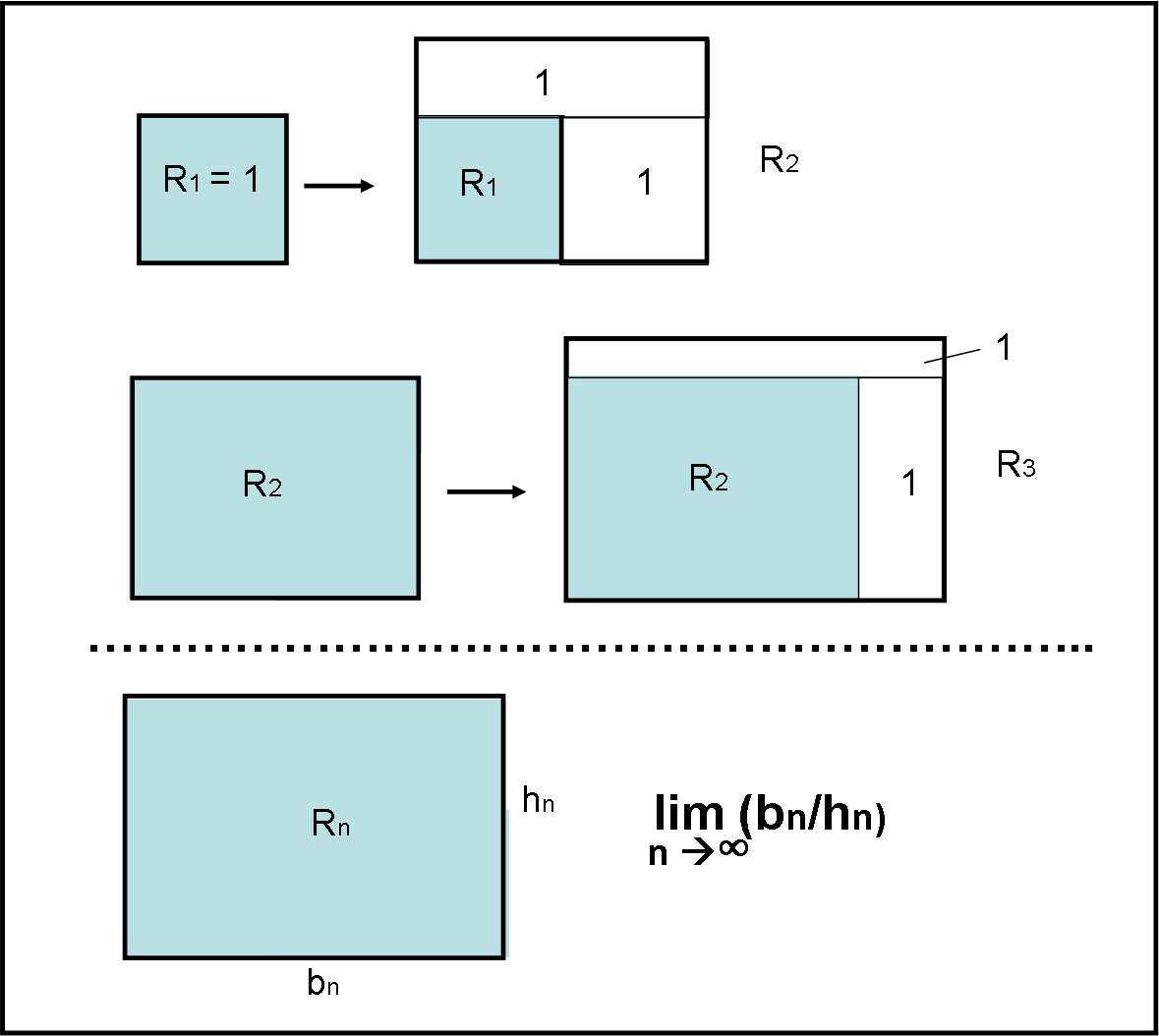
Partiamo da un quadrato di lato uguale a 1 (e di area uguale a 1). Lo consideriamo come rettangolo di inizio, R1.  Al secondo passo aggiungiamo sulla destra un altro quadrato di lato unitario, ottenendo un rettangolo di base = 2 e di altezza = 1.  Sulla parte superiore inseriamo un nuovo rettangolo che abbia come area sempre 1. Ovviamente, la sua base sarà adesso uguale a 2 mentre la sua altezza sarà solo 1/2. Otteniamo un secondo rettangolo R2.

Continuiamo il giochino su R2. A destra aggiungiamo un rettangolo di area 1 e lo stesso facciamo sulla parte superiore. In tal modo otteniamo un nuovo rettangolo R3…

La costruzione ci porta a un rettangolo ennesimo che avrà una certa base bn e una certa altezza hn.

Quello che vogliamo determinare è il limite, per n che tende a infinito, del rapporto tra base e altezza del rettangolo.

Il  calcolo del limite ha bisogno di passaggi successivi più complicati. A quel punto, qualcuno avrà , però, già riconosciuto con cosa abbiamo a che fare e il risultato si potrà anche ricavare in modo … “manuale” con n abbastanza grande.

Le operazioni da svolgere sono illustrate nella figura che segue. Il risultato ci permetterà anche di accennare a un personaggio non trascurabile nella storia della matematica.

rettangolo1

 

QUI la soluzione

QUI tutti i quiz del blog

Articoli correlati

16 commenti

  1. Arturo Lorenzo
    17/03/2018 at 15:00

    Provo a smuovere un po' le acque.

    Ho provato a eseguire i conti manualmente un caso per volta partendo dal quadrato iniziale.

    Ottengo (indicando con A l'area b*h ):

    caso 1) b=1 ; h=1; A=1 ; b/h =1

    caso 2) b=2; h=1,5; A=3; b/h=1,333

    caso 3) b=2,667; h=1,875; A=5; b/h=1,422

    caso 4) b=3,200; h=2,187; A=7; b/h=1,463

    caso 5) b=3,675; h=2,461; A=9; b/h=1,486

    caso 6) b=4,063; h=2,707; A=11; b/h=1,501

    a questo punto non ho resistito e ho implementato l'algoritmo di crescita dei lati del rettangoli in un foglio Excel, arrivando subito al caso 2000-esimo  (ma potrei andare ben oltre , memoria RAM permettendo)  :mrgreen:

    Base e altezza crescono sempre, anche se l'aumento n-esimo è inferiore a quello precedente. Le due rispettive curve sembrano molto quelle di un funzione del tipo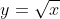 y=\sqrt{x}.   Il loro rapporto, invece, aumenta rapidamente nei primi casi per poi stabilizzarsi , credo asintoticamente, al valore 1,57, che guarda caso somiglia tanto a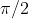 \pi /2

    Allego il grafico degli andamenti di b (curva rossa), h (curva verde) e b/h (curva blu):

    grafico ottenuto con Excel

    Non ho , però, dimostrato nulla, ovvio. Ho solo constatato che il limite del rapporto è 1,57.

     

     

  2. Vincenzo Zappalà
    17/03/2018 at 15:07

    cerca di trovare il termine ricorrente (se esiste...)... Poi si vedrà.... :wink:  :wink:

  3. Fabrizio
    17/03/2018 at 18:49

    Queste espressioni credo siano valide per ogni passo (R è l'area del rettangolo)

    \begin{align*} R_n &=2 n-1 \\ h_n&=R_n/b_n \\ \end{align*}

    Partendo da queste espressioni si possono ricavare queste relazioni tra i valori di b ed h in un passo generico con i valori del passo precedente

    \begin{align*} b_n &=b_{n-1}+\frac{1}{h_{n-1}}=b_{n-1} \frac{R_{n-1}+1}{R_{n-1}} \\ h_n &=\frac{R_n}{b_n}= \frac{R_{n-1}}{b_{n-1}}\frac{R_n}{R_{n-1}+1}=h_{n-1} \frac{R_n}{R_{n-1}+1}\\ \frac{b_n}{h_n}&=\frac{b_{n-1}}{h_{n-1}} \frac{(R_{n-1}+1)^2}{R_{n-1}R_n}\\ \frac{b_n}{h_n} &=\frac{b_{n-1}}{h_{n-1}} \frac{(2n-2)^2}{(2n-3)(2n-1)} \end{align*}

    a numeratore c'è il quadrato di un numero pari e a numeratore i due numeri dispari adiacenti.

    Quindi il rapporto tra base ed altezza di uno dei rettangoli dovrebbe essere

    \frac{b_n}{h_n}=1\cdot \frac{2^2}{1\cdot2}\cdot \frac{4^2}{3\cdot5}\cdot \frac{6^2}{5\cdot7}\cdot\cdot\cdot\cdot \frac{(2n-2)^2}{(2n-3)\cdot(2n-1)}

    Potrebbe essere questa l’espressione da trattare manualmenet alla quale si riferiva Enzo.

    Per trovare più formalmente il limite di questa espressione credo si debba tradurla in fattoriali, ma finora non ho trovato nulla di trattabile.

     

  4. Vincenzo Zappalà
    17/03/2018 at 18:59

    mmmmmhhhh... mi sa che qualcosa non vada bene....  (non c'è bisogno di frattali... temo che il termine generico sia da elaborare o da riguardare un po'...).

  5. Andy
    17/03/2018 at 20:27

    Io ho voluto lavorare "all'antica", carta e matita, ma concordo con Arturo circa la convergenza del rapporto b/h a π/2.

    https://i.imgur.com/yg3Gy0J.jpg

    https://i.imgur.com/qQpqAFV.jpg

    Per l'algoritmo...attendere, prego :mrgreen:

  6. Fabrizio
    17/03/2018 at 22:19

    Ho riguardato l'espressione generica che ho ottenuto. Mi sembra corretta.

    \frac{b_n}{h_n} =\frac{b_{n-1}}{h_{n-1}} \frac{(2n-2)^2}{(2n-3)(2n-1)}

    C'era solo un errore nel secondo fattore dello sviluppo (Avevo battuto 2 invece di 3).

    \frac{b_n}{h_n}=1\cdot \frac{2^2}{1\cdot3}\cdot \frac{4^2}{3\cdot5}\cdot \frac{6^2}{5\cdot7}\cdot\cdot\cdot\cdot \frac{(2(n-1))^2}{(2n-3)\cdot(2n-1)}

    Effettivamente non c'è bisogno di convertirla in fattoriali.

    Ho trovato che l'espressione corrisponde al prodotto di Wallis, che finora non conoscevo assolutamente.

    Il suo limite all'infinito corrisponde proprio a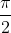 \frac{\pi }{2}.

    Frequentando il circolo si impara sempre qualcosa.

     

  7. Vincenzo Zappalà
    18/03/2018 at 07:20

    caro Fabry,

    era solo il termine ricorrente che cambia ...io ho trovato quello ennesimo...

    Sì, mi è piaciuto molto, perché in origine si dovrebbe lavorare con funzioni trigonometriche ed è veramente inaspettato che lo stesso prodotto infinito venga ricavato da rapporti di lunghezze... Pigreco ne sa una più del diavolo... :lol:

  8. Fabrizio
    18/03/2018 at 10:44

    Si, veramante inaspettato. Solo dopo la deduzione di Arturo ho mosso in relazione il risultato con pi greco.

    Le dimostrazioni che ho finora trovato in rete sono tutte analitiche. Chissà se ce ne è qualcuna geometrica.

    Il rapporto tra b ed h finali è quello della lunghezza di 1/4 di circonferenza ed il suo raggio o il rapporto tra area del rettangolo e h finali è quello dell'area di un semicerchio con il suo raggio. Questi rapporti convergono, ma non converge il rettangolo che diventa infinito.

  9. Vincenzo Zappalà
    18/03/2018 at 11:04

    forse meriterebbe investigare... chissà... :roll:

  10. Andy
    18/03/2018 at 12:18

    È  il rapporto tra l'area di un cerchio qualsiasi e l'area del rettangolo costruito sul suo diametro e di altezza pari al raggio. Sarebbe interessante, se esiste, conoscere l'algoritmo per trovare l'n-esimo lato del rettangolo senza iterativamente conoscere il precedente.

  11. Fabrizio
    18/03/2018 at 17:55

    Andy,

    non so se ho capito bene la tua domanda.

    Se ti riferivi al rettangolo del quiz i lati dovrebbero essere questi per n>1:

    \begin{align*} b_n &= \prod_{j=1}^{n-1}\frac{2j}{2j-1}\\ h_n &= (2n-1)\prod_{j=1}^{n-1}\frac{2j-1}{2j} \end{align*}

     

     

  12. Andy
    18/03/2018 at 20:41

    Perfetto Fabrizio, era proprio questa la mia domanda, che hai sviluppato eccellentemente.

    Così, per gioco, ho fatto il calcolo (o meglio, l'ha fatto il computer che è più veloce di me :mrgreen: ) delle prime 99999 iterazioni, calcolando il centomillesimo termine rispettivamente di b, h, b/h:

    n=100000

    b=560.49701976502148521680

    h=356.82437719980395648285

    b/h=1.57079239978935337404

     

    E così, dopo 99999 iterazioni, il valore del rapporto che tende a π/2, coincide con esso solo fino alla 5a decimale.

    Ne deve fare ancora di strada il ragazzo-rapporto! :lol:

     

  13. Fabrizio
    18/03/2018 at 22:33

    Infatti, negli articoli che trattano il prodotto di Wallis si dice spesso che non è utilizzato per il calcolo di π proprio per la sua lentezza a convergere.

  14. Andy
    19/03/2018 at 00:36

    Una piccola curiosità:

    il rapporto tra due numeri interi determina un valore aderente a π sino alla 37a decimale:

    2.646.693.125.139.304.345 / 842.468.587.426.513.207 = 3,1415926535897932384626433832795028841

     

    Chissà che Enzo non scriva un bell'articolo dei suoi sul π :wink:

  15. Vincenzo Zappalà
    19/03/2018 at 07:43

    cari amici,

    purtroppo ho problemi di modem e facilmente la linea salterà tra poco (è da ieri che vado avanti così). l'idea dell'articolo dedicato a pigreco è molto bella. Nel frattempo, potreste dare un'occhiata a questo e pi mi sembra di avere scritto altro, ma è meglio chiedere a Scherzy...

    http://www.infinitoteatrodelcosmo.it/2015/03/15/il-giorno-del-pigreco/

  16. PapalScherzone
    19/03/2018 at 09:28

    Eccomi! :-D

    Sul pi-greco abbiamo anche questo

    http://www.infinitoteatrodelcosmo.it/2015/11/20/41-archimede-e-lesaustione/

    Archimede arrivò a questo risultato:

    3.140845 < π <  3.142857

    In poche parole, determinò con esattezza le prime due cifre decimali. Vi sembra poco per quei tempi? Era più che sufficiente per disegnare un quadrato che avesse un’area molto simile a quella del cerchio.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.