Vi sono state risposte molto accurate al quiz e non mi resta che riportare la soluzione nel modo più semplice e dettagliato possibile. In modo quasi imprevisto, è saltato fuori il solito, immancabile, π. Un dovuto omaggio proprio in concomitanza con il giorno dell’anno dedicato a lui. Forse, tra non molto, sarebbe il caso di dargli una visibilità ancora più ampia, a partire dalla storia antica (nel frattempo, QUI potete leggere di come Archimede riuscì ad approssimare le prime due cifre decimali).

Ripartiamo dalla figura proposta e iniziamo a costruire i nostri primi due rettangoli.

 

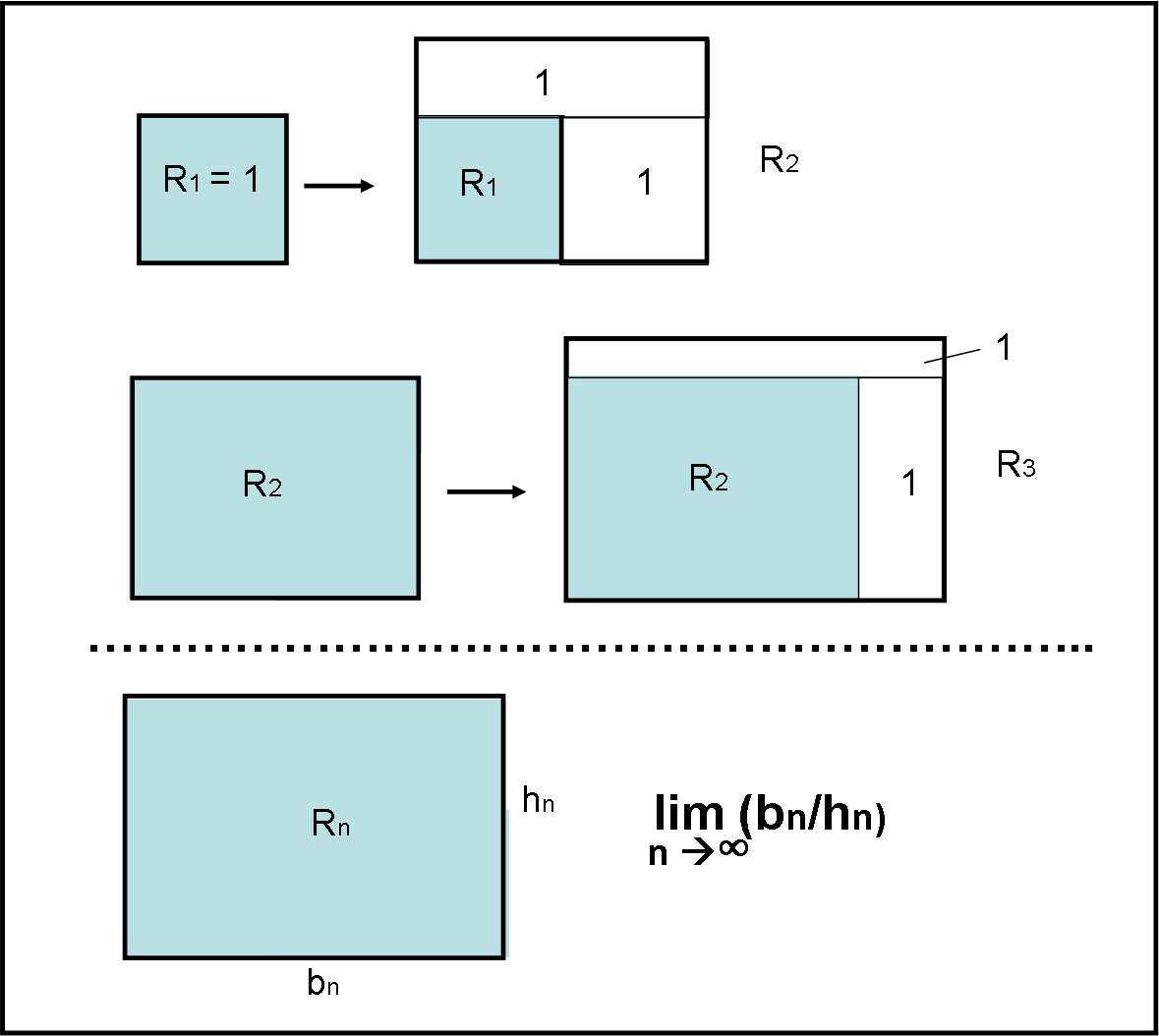
Partiamo da un quadrato che ha come rapporto tra base e altezza proprio l’unità:

b₁/h₁ = 1/1 = 1

Ovviamente, l’area del quadrato è

R₁ = 1

Aggiungiamo le aree unitarie a destra e in alto, come previsto dalla costruzione. L’area a destra è tale e quale al quadrato di partenza. Ciò vuol dire che la base del nuovo rettangolo ha lunghezza 1 + 1 = 2. Ne segue che il rettangolo unitario da inserire in alto dovrà avere lunghezza 2 e altezza ½ (l’area deve rimanere unitaria). Otteniamo, quindi, per R₂ una base uguale a 2 e un’altezza pari a 1 + 1/2, ossia 3/2. In formula:

b₂/h₂ = 2/(3/2) = 4/3 = (2/1)(2/3)

Ciò vuole anche dire che la sua area vale:

R₂ = 2· 3/2 = 3

Andassimo avanti di un rettangolo troveremmo che l’area  di R₃ sarebbe uguale a 5 (d’altra parte ogni rettangolo aumenta la sua area di due unità, per costruzione).

In generale, possiamo già concludere che per un valore n del rettangolo, si ha:

R_n = 2n - 1                …. (1)

Possiamo fermarci qui e passare al rettangolo ennesimo per costruire quello successivo.

Il rettangolo ennesimo ha base uguale a b_n e altezza uguale ad h_n. Il rettangolo unitario da aggiungere a destra (proprio perché unitario)  ha la base uguale a 1/h_n (deve essere: h_n·1/h_n = 1). Ne segue che la nuova base sarà:

b_n+1 = b_n + 1/h_n

Questa è anche la base del rettangolo da aggiungere nella parte alta, che, quindi, per essere di area unitaria, deve avere altezza uguale a :

1/b_n+1 = 1/(b_n + 1/h_n) = h_n/(h_nb_n + 1)

Attenzione! h_nb_n non è altro che l’area del rettangolo ennesimo e possiamo scriverla come 2n – 1, seguendo la (1).

Ne segue che l’altezza del rettangolo da aggiungere nella parte alta è uguale a:

1/b_n+1  = h_n/2n

L’altezza del rettangolo n+1esimo sarà, allora:

h_n+1 = h_n + h_n/2n

Facciamo il rapporto tra base e altezza:

b_n+1/h_n+1 = (b_n + 1/h_n)/(h_n + h_n/2n)

b_n+1/h_n+1 = (2n)(h_nb_n + 1)/(h_n² (2n + 1))

b_n+1/h_n+1 = (2n)(2n)/(h_n² (2n + 1))

giochiamo un po’ con h_n²…

h_n² = b_nh_n/(b_n/h_n) = (2n -1)/(b_n/h_n)

Sostituendo :

b_n+1/h_n+1 = (b_n/h_n)(2n)(2n)/((2n -1) (2n + 1))

Ovviamente, b_n/h_n può essere scritto in funzione di n -1 e via dicendo fino ad arrivare al primo rettangolo. Abbiamo di fronte un prodotto continuo dei rapporti tra base e altezza dei rettangoli consecutivi …

Cominciamo da n = 1

b₂/h₂ = (b₁/h₁) (2·1)(2·1)/((2 - 1) (2 + 1)) = (1/1)·2·2/(1·3) = (2/1)(2/3)

b₃/h₃ = (b₂/h₂) (2·2)(2·2)/((4 - 1)(4 + 1)) = (2/1)(2/3)·(4/3)(4/5)

b₄/h₄ = (b₃/h₂) (2·3)(2·3)/((6 – 1)(6 + 1)) = (2/1)(2/3)·(4/3) (4/5)·(6/5)(6/7)….

In poche parole:

lim _n→∞ b_n/h_n = ∏_{k =1}^∞ (2k/(2k -1))(2k/(2k +1))

che altri non è che il prodotto infinito di Wallis e vale π/2.

Come faccia un rettangolo, la cui area cresce di 2 unità alla volta e la cui base e altezza si adeguano alla situazione, a portarci verso π è una delle sue tante meraviglie. Ma da un numero così… irrazionale ci si può aspettare di tutto. Il prodotto di Wallis (1655) non è certo rapidissimo nel convergere, ma ha dalla sua una grande facilità di calcolo.

Non è nemmeno difficile dimostrare il risultato.

Basta considerare il rapporto sin(x)/x ed esprimerlo attraverso il prodotto infinito di fattori lineari, basati sulle sue radici (+/- nπ), moltiplicato per una certa costante. Passando al limite per x che tende a zero, il prodotto tende alla costante che deve essere uguale a 1 (il limite di sin(x)/x è infatti uno per x che tende a zero… me lo avevano chiesto alla maturità…). Ne risulta che sin(x)/x è esattamente uguale al prodotto  dei fattori lineari, introdotti prima.Con semplici passaggi algebrici  e calcolandolo per x = π/2, si ottiene che sin(π/2)/(π/2) = 2/π è uguale a ∏₁^∞(4n² -1)/4n². In altre parole:

π/2 = ∏₁^∞ 4n²/(4n² – 1) = ∏₁^∞ (2n/(n-1))·(2n/(n+1))

che è proprio il prodotto di Wallis.

Vi sono, in realtà, praticamente infiniti metodi per calcolare π, quasi quante le sue cifre decimali. Potrebbe essere interessante farne una piccola storia, partendo ancora prima di Archimede. Lo tengo a mente…

 

Detto fatto, ecco QUI la storia infinita del pi greco!

QUI tutti i quiz del blog