Categorie: Matematica
Tags: approssimazioni successive area rettangolo area triangolo integrali definiti sommatorie
Scritto da: Vincenzo Zappalà
Commenti:10
42. Calcoliamo l'area del rettangolo e del triangolo *
Non vi arrabbiate se vi sto trattando come dei bambini... ma in questo articolo non facciamo altro che calcolare l'area del rettangolo e poi attraverso di lei tentare con qualcosa di molto più "strano" (un triangolo). In fondo, stiamo solo imitando Archimede e non è certo un'offesa!
Per impostare il problema nel modo più semplice e comprensibile, torniamo ancora sul moto rettilineo uniforme e sull’ormai “celebre” rettangolo che ci regala lo spazio percorso, nota la velocità costante. Lasciamo perdere la velocità e ragioniamo in termini di x e y e di area compresa tra la funzione y = c = costante e l’asse x, nell’intervallo (O,b). In altre parole vogliamo nuovamente calcolare l’area del rettangolo OACB. No, non ditemi che ormai la conoscete più che bene… Noi vogliamo adesso mostrare il vero procedimento che si usa per ottenere quella formuletta che sanno anche i bambini.
Cosa vuol dire eseguire il prodotto di y per x? Ricordiamo che un prodotto non è altro che una somma ripetuta: (2 x 5 = 2 + 2 + 2 +2 + 2). Immaginiamo di dividere il lato x in tanti segmenti dx, tutti uguali (ad esempio, potrebbe proprio essere l’unità di misura delle x). Disegniamo la Fig.1, dove potremmo, comunque, rendere sempre più piccola la lunghezza del segmentino dx.
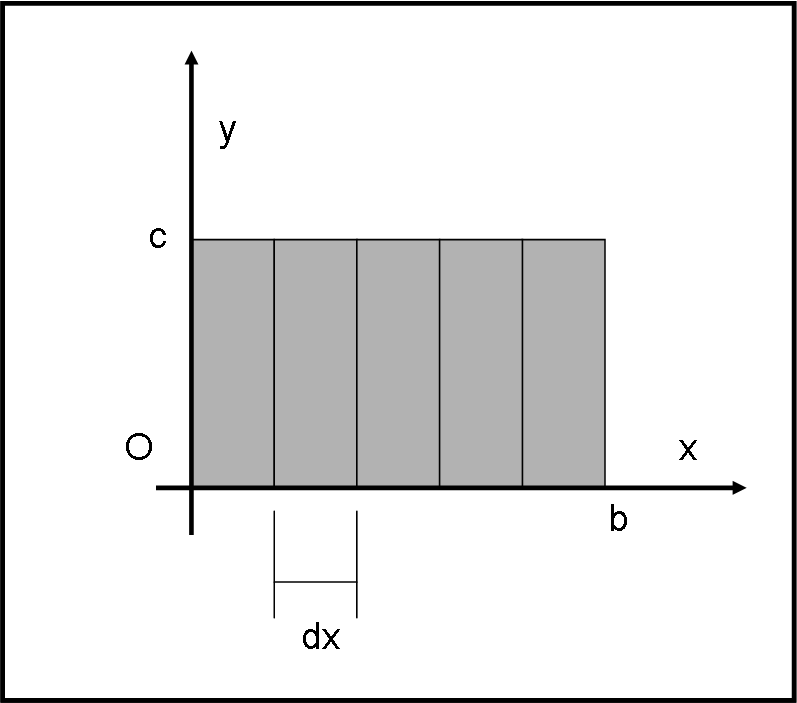
Vi pregherei, comunque, data la banalità di queste nozioni, di non correre avanti tralasciando queste frasi apparentemente “elementari”. Proseguiamo piano piano, senza fretta, solo così l’integrale ci apparirà un’ovvia conclusione.
Come si calcola l’area del rettangolo? Beh… facilissimo: possiamo sommare tutte le aree dei rettangolini di lati dx e c, compresi nell’intervallo prescelto. Se abbiamo diviso il lato lungo x (segmento b) in n segmentini dx, l’area del rettangolo sarà data da A = n·c·dx. Per essere più rigorosi utilizziamo un simbolo che ormai conosciamo molto bene:
A = c Σnk = 1 dxk
ma dxk = dx è una costante, per cui:
A =c dx Σnk = 1 1 = c n dx = c b (n dx = b)
Ricordo che
Σnk = 1 1 = 1 + 1 + 1 + 1 + …. + 1 = n
Da non confondere con:
Σnk = 1 k = 1 + 2 + 3 + 4 + …. + n
Ovviamente, n può essere preso grande a piacere… anche infinito (passando al limite)
A = limn→∞ c Σnk = 1 dxk
In pratica, ciò vorrebbe dire aumentare in modo enorme il numero di rettangolini che sono compresi nel segmento di lunghezza b. Al limite, prendendone infiniti, facendo tendere a zero la loro lunghezza, come mostra la Fig. 2, dove si è ridotta la lunghezza di dx. Non ditemi, ovviamente, che se l'area tende a zero la somma di tanti zero non può che essere zero! Dobbiamo ricordarci che n tende a infinito e... zero per infinito è un limite indeterminato che può avere come risultato un valore finito...
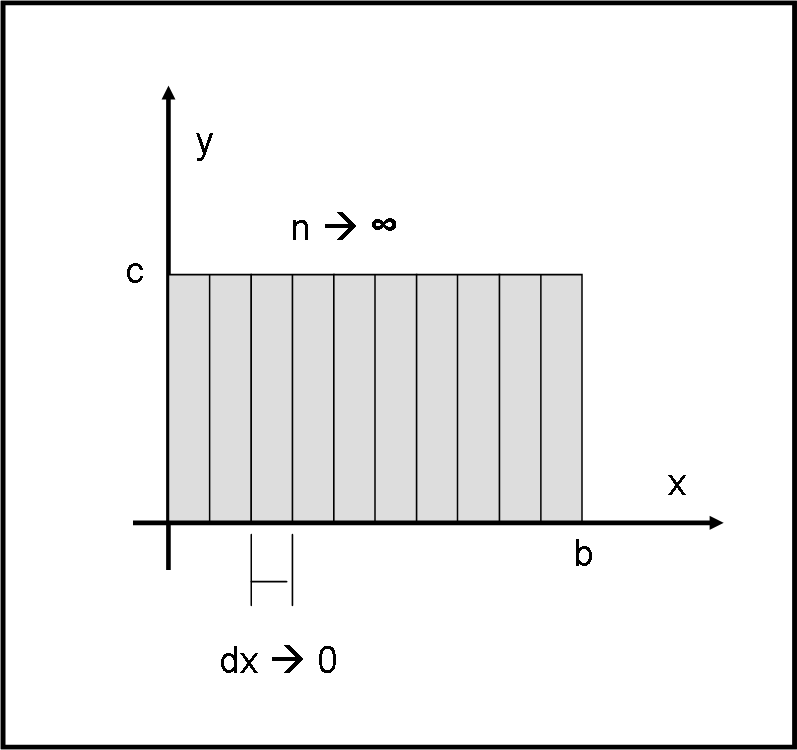
Nel caso in esame, la funzione è uguale a una retta parallela all’asse x e l’ area è quella del rettangolo compreso tra O e b. Tutto questo discorso matematico diventa quasi assurdo, dato che stiamo trattando il caso in cui y = c e quindi non vi è nessun bisogno pratico di fare una sommatoria e ancor di più passare al limite, aumentando sempre più il numero di intervallini e di rettangoli contenuti nel “rettangolo” finale. In questo semplice caso non ve n’è bisogno dato che la sommatoria è facilmente calcolabile, essendo la lunghezza del segmento che rappresenta la base del rettangolo.
Ammetto che quest’approccio sembra veramente una presa in giro, ma ci dà le basi per il passaggio successivo, ben più importante. Possiamo, infatti, dire di conoscere come calcolare l’area di un rettangolo di dimensioni qualsiasi e perché . Un gatto che si morde la coda, ovviamente, ma che ci ha permesso di introdurre il sistema operativo che utilizzeremo d’ora in avanti. Il rettangolino è la nostra “briscola”!
Proseguiamo con un piccolo esercizio...
Consideriamo come funzione una retta passante per l'origine e inclinata di 45°. La sua equazione è
y = x
Cerchiamo l'area compresa tra questa retta e l'asse delle x, delimitata, inoltre, dall'asse y e dalla retta x = 3.
Noi sappiamo calcolare soltanto l'area del rettangolo (lato per lato diviso due) e dobbiamo cercare di calcolare l'area della "strana" figura della Fig. 3 (è un triangolo, ma non diciamolo a nessuno...).
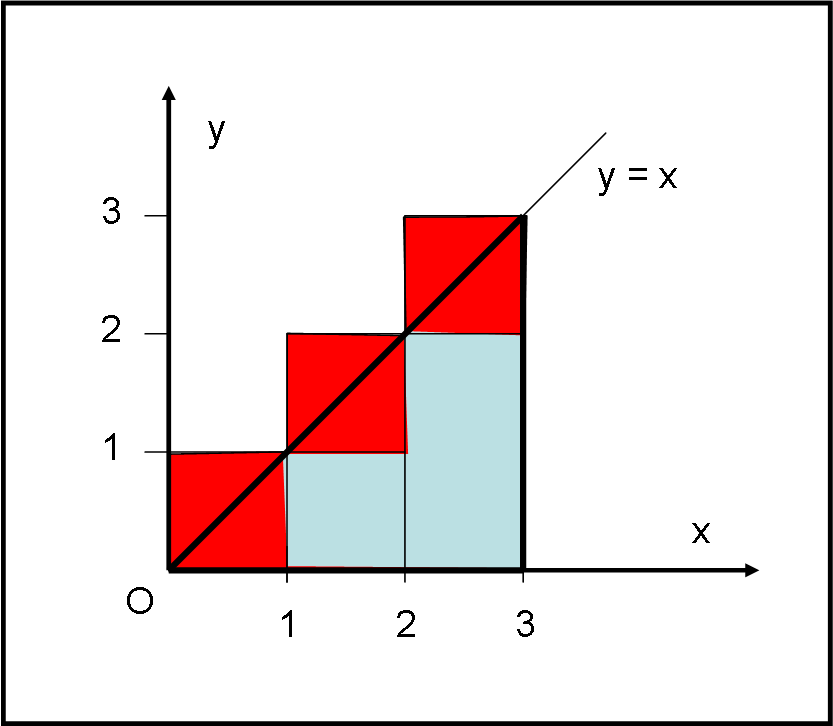
Non ci resta che seguire l'esempio di Archimede... Dividiamo il segmento in n intervallini dx uguali all'unità (tanto per cominciare), per cui, nel nostro caso, n = 3. Per ogni intervallino costruiamo il rettangolino che sta sotto alla retta y = x. Esso ha come lato verticale la y minima assunta dalla funzione nell'intervallo dx scelto. Ricordando che y = x, sarà anche dy = dx = 1. Il primo intervallo ha, quindi, come lato verticale dy = 0 (nessun rettangolo), il secondo rettangolo ha come lato y = dy = dx = 1; il terzo e ultimo y = 2dy = 2dx = 2.
Non ci resta che calcolare le aree dei rettangoli corrispondenti. Il primo ha area 1 · 0; il secondo 1 · 1 = 1; il terzo 2 · 1 = 2
La somma dei rettangoli, sotto la funzione, è data allora da 0 + 1 + 2 = 3 (parte azzurra)
Ripetiamo lo stesso esercizio, costruendo degli altri rettangoli, considerando gli stessi intervallini dx, ma con il lato verticale uguale al valore massimo della funzione y = x, nell'intervallo dato.
Il primo intervallo ha come lato verticale y = dy = dx = 1; il secondo ha come lato 2dy = 2dx = 2; il terzo 3dx = 3
La somma dei rettangoli esterni (sopra la funzione) è data, adesso, da: 1 + 2 + 3 = 6 (parte azzurra più quella rossa)
Possiamo concludere che l'area A della "strana" figura deve essere:
3 < A < 6
Non abbiamo ottenuto molto, ma è solo l'inizio.
Non ci perdiamo d'animo e continuiamo, dividendo a metà l'intervallino dx, che sarà adesso dx/2 = 1/2. Analogamente per dy = dx/2 = 1/2. Si vede chiaramente (provate...) che ci si avvicina sempre di più alla strana figura sia da sotto che da sopra. Quanto valgono le due aree corrispondenti? E cosa succede se dividiamo ancora dx/2 per 2, ossia considerando come intervallino 1/4?
Queste ulteriori approssimazioni potete farle da soli e calcolare le aree interne ed esterne che si avvicinano sempre di più all'area cercata. Imitate, in qualche modo, Archimede.
Non c'è certo bisogno che vi dia il risultato... dato che la strana figura non è altro che un triangolo di base 3 e di altezza 3, ossia di area uguale a 4.5.
Bene, sembrerebbe uno scherzo o poco di più... ma ormai siamo pronti a calcolare qualsiasi area!
QUI il capitolo precedente
QUI il capitolo successivo
QUI l'intero corso di matematica






10 commenti
Caro Enzo seguendo lo schema che indichi nell'articolo, ho usato dei rettangoli sempre più piccoli per approssimare meglio l'area.
Anche se ho indicato i passaggi matematici, basta guardare le figure per capire cosa cambia usando rettangoli sempre più piccoli.
Nella Prima illustrazione l'intervallo in cui si suddivide la figura è ½ dx (i lati dei corrispondenti rettangoli sull'asse x sono ½ dell'unità di misura 1)
http://www.astrobin.com/full/225997/G/
Nella seconda illustrazione l'intervallo in cui si suddivide la figura è ¼ dx
http://www.astrobin.com/full/225997/H/
Nell'ultima illustrazione l'intervallo in cui si suddivide la figura è 1/10 dx.
In questa figura ho anche provato a “costruire” una formula generale compatta (spero che la scrittura sia corretta...), in cui gli intervalli di dx sono stati indicato come ds ed il numero di intervalli in cui si suddivide la figura è stato indicato come n.
http://www.astrobin.com/full/225997/I/
Ovviamente riducendo l'intervallo ds, aumenta il numero dei rettangoli e migliora l'approssimazione.
Per esempio usando la formula descritta nella figura ed un intervallo di 1/1000 dx:
Area (esterna) = (1/1000)² Σ3000k = 1 = 4501500/1000000 = 4,5015
Area (interna) = (1/1000)² Σ2999k = 1 = 4498500/1000000 = 4,4985
Paolo
caro Paolo,
sono molto contento che non ti sia sentito preso in giro a eseguire calcoli così banali. Infatti, hai notato benissimo come si faccia in fretta a introdurre una sommatoria e una serie (se ne potevano anche trovare altre) per definire il problema in modo sintetico. Serie e sommatorie sono proprio quelle che ci portano per mano agli integrali. L'umiltà scientifica rende tutto più facile. Complimenti soprattutto per quest'ultima dote!
A mio avviso le questioni che sembrano semplici, in realtà nascondono le basi di una complessità indispensabile per affrontare le questione più complesse.
In fin dei conti per ora stiamo applicando un metodo ad una funzione semplice y=x, ossia a una retta con coefficiente angolare m=1..... se non si capisce a fondo come trattare il calcolo di aeree “semplici”, come si può pensare di trattare funzioni più complesse (parabole, cubiche, o peggio curve qualsiasi)?
Quindi non conviene snobbare il calcolo di aree di poligoni semplici (quadrati, rettangoli, triangoli).
A proposito, per calcolare le Aree suddivise in rettangoli con ds = 1/1000, non ho certo sommato l'area di 3000 rettangoli ..... mi è toccato cercare una formula capace di trovare velocemente il risultato della sommatoria
..... mi è toccato cercare una formula capace di trovare velocemente il risultato della sommatoria
1 + 2 + 3 + 4 + 5 +6 + 7+ ............ +n = n (n+1)/2
Una formuletta trovata in rete che non potevo certo accettare senza cercare di coglierne il significato....
Ho tentato, perciò di capire come ricavarla
http://www.astrobin.com/full/225997/J/
Mi sa che manca ancora qualcosa a questo tentativo..... però quanto trovato usando solo un po' di logica consente di sommare velocemente un numero enorme di rettangolini, dato che la formula finale dell'ultima figura del precedente post (non la scrivo, poiché risulterebbe incomprensibile, dato che il sito non consente l'uso di apice e pedice), diventa:
però quanto trovato usando solo un po' di logica consente di sommare velocemente un numero enorme di rettangolini, dato che la formula finale dell'ultima figura del precedente post (non la scrivo, poiché risulterebbe incomprensibile, dato che il sito non consente l'uso di apice e pedice), diventa:
A (esterna) = ds ² n (n+1)/2
A (interna) = ds ² (n-1) ((n-1) +1)/2 = ds ² (n-1) n/2
ds ² n (n-1)/2 < A < ds ² n (n+1)/2
Paolo
Quella che hai usato è una serie aritmetica divergente (la somma dei numeri n interi) e si può dimostrare che vale proprio n(n+1)/2. Sembra una cosa facilissima e, invece, c'è riuscito Gauss attraverso un trucco niente male. Ha eseguito la somma da 1 a n e la somma da n a 1, ecc., ecc.
Ogni serie ha dietro di sé una storia che ha impegnato fior fiore di matematici. Primaa o poi ci divertiremo anche con loro...
Anzi, quasi... quasi domani butto giù il procedimento usato da Gauss, dove ha dimostrato che la logica permette di evitare -spesso e volentieri- inutili calcoli! Che ne dite?
Bellissimo!
Se non mi sto confondendo con qualcos'altro (niente di più probabile!!), ho letto da qualche parte il modo in cui Gauss ha trovato la formula per sommare n numeri interi consecutivi e la cosa sorprendente è che, quando l'ha fatto, era poco più che bambino... o sbaglio?!
D'accordissimo
Paolo
non sbagli; dicono che il maestro di scuola per punizione o per farli star buoni abbia imposto di fare la somma dei primi 120 numeri interi; del resto senza la sua mente privilegiata lo sviluppo scientifico sarebbe andato a rilento.. basta pensare ai suoi contributi all'elettromagnetismo, e alla Teoria della relatività generale che senza le basi della sua geometria differenziale e del suo allievo Riemann (nonchè dei nostri Ricci e Levi Civita) forse potrebbe anche non esistere ancora
Caro Prof.
nella sua lezione n.42
http://www.infinitoteatrodelcosmo.it/2015/11/25/42-calcoliamo-larea-del-rettangolo-e-del-triangolo/
ad un certo punto lei scrive : da non confondere con...ed invece io ammetto che mi confondo, potrebbe
per cortesia spiegarmi meglio la differenza ?
La prima parte Σnk = 1 sembra uguale per entrambe, ma poi prosegue diversamente! Cosa significa ?
Σnk = 1 1 = 1 + 1 + 1 + 1 + …. + 1 = n
Da non confondere con:
Σnk = 1 k = 1 + 2 + 3 + 4 + …. + n
cara Emma,
Σnk = 1 1 = 1 + 1 + 1 + 1 + …. + 1 = n
vuol dire sommiamo il numero 1 tante volte quanto dice k, che va da 1 a n. Il che vuol dire sommare n volte il numero 1, che non cambia al variare di k, dato che è una costante.
Infatti, per k = 1, 1 vale 1
per k = 2, aggiungiamo un altro 1
per k = 3, aggiungiamo un altro 1
per k = n, aggiungiamo l'ennesimo 1
alla fine abbiamo la somma di n volte 1, ossia n
Da non confondere con:
Σnk = 1 k = 1 + 2 + 3 + 4 + …. + n
che è la somma di un numero k (non è più una costante!) che va da 1 a n, come prima, ma esso cambia al variare di k
per k = 1, vale k, ossia 1
per k = 2, vale k, ossia 2
per k = 3, vale k, ossia 3
...
per k = n, vale sempre k, ossia n
ne segue che sommiamo 1 a 2 a 3..... a n-1 e a n
ossia 1 + 2 + 3 +.... + n
che è cosa ben diversa.