Non ce ne sarebbe bisogno, perchè il quiz è stato ampiamente risolto. Comunque, se qualcuno non avesse capito bene i passaggi li faremo uno ad uno.

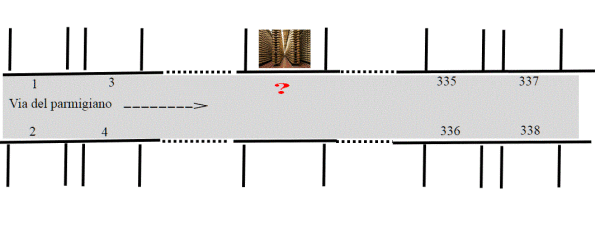
Il quiz richiedeva di trovare il numero civico del negozio, sapendo che la somma dei civici che lo precedono (dallo stesso lato) fosse uguale alla somma dei civici che lo seguono , quindi k è escluso da entrambe le somme Si sa inoltre che l'ultimo numero dal lato del deposito è 337.

Soluzione: chiamiamo k tale numero. K è un numero dispari, in quanto sta nello stesso lato di 337.Noi dobbiamo considerare i numeri dispari. Quanti sono i numeri dispari che precedono k?  sono . Infatti, e per esempio k=7, abbiamo che  1,3,5 precedono k, e sono (7-1)/2=3.k=9,  1,3,5,7=(9-1)/2=4. Chi è pignolo può dimostrarlo per induzione.  In un miniquiz abbiamo dimostrato che la somma dei primi n numeri dispari, è uguale al quadrato di n. Quindi la prima somma, quella dei numeri dispari inferiori a k ,chiamiamola Sk-1, è  . La somma invece di tutti i numeri dispari che vanno da 1 a 337 è .  Infatti, nella formula dobbiamo mettere  il valore dei numeri dispari da 1 a 337 che sono 338/2=169. Chiamiamo tale somma Sn .Vediamolo sempre con un esempio: se n=5, abbiamo 1,3,5 che sono (5+1)/2=3. Anche qui si può dimostrarlo per induzione. Per ottenere la somma dei numeri che seguono k ,come facciamo ? Non possiamo applicare direttamente la formula del quadrato, perchè i numeri non partono da 1. Ma possiamo ottenerla, togliendo a Sn la somma dei primi k numeri, . Infatti fino a k compreso abbiamo k+1 numeri dispari. Solito esempio: k=7, 1,3,5,7 che sono (7+1)/2=4.

Possiamo allora impostare la seguente equazione ad un incognita:

 e abbiamo finito.

Ma purtroppo il topo logico non ha ancora risolto tutti i problemi.. lo vedremo alla prossima puntata.