Quiz:La chiave del deposito
Se pensavate che il Topo-logico avesse risolto i suoi problemi eco-gastronomici una volta trovato il numero civico del deposito (quiz precedente) siete stati ottimisti. Purtroppo non è così, il topo una volta raggiunto il deposito trova una brutta sorpresa.. niente meno che una porta blindata, stile cassaforte e indistruttibile. E' si, nell'isola di Groviera il formaggio è più prezioso dell'oro!
L'apertura della porta , che è all'avanguardia, prevede una combinazione a tre cifre digitali; vi sembrano poche? In realtà non lo sono, perchè se si sbaglia due volte la combinazione la cassaforte si blocca per sempre.
Infatti , sotto la tastiera digitale, si trova una targa, scritta dal matematico-formaggiaio Don Alfonso di Groviera:
"Attenzione, se si sbaglia due volte la combinazione di tre cifre, la cassaforte non si aprirà mai più".
A questo punto il topo-logico rischia il suicidio.. ma poi decide di tornare in biblioteca, a rovistare sui giornali che parlano del deposito.
Niente da fare, non si trova niente a riguardo della combinazione. Ma poi il topo riflette; ma sono diventato scemo? Come potrebbero scriverlo sui giornali; deve esserci qualcosa che riguarda come sempre il matematico -formaggiaio. Allora decide di cercare perchè Don Alfonso di Groviera sia stato un grande matematico, finchè trova il perchè:
" ..Don Alfonso di Grovierà è passato alla storia della matematica, per aver scoperto che esistono (solo) due numeri di tre cifre (ovvero dei numeri n, con 100<=n<=999) che se elevati al quadrato danno un numero in qui le tre cifre finali sono uguali al numero di partenza. In pratica se xyz è un numero a tre cifre, e x,y,z rappresentano tali cifre, =ab..xyz. Egli scopri in seguito che questo è vero anche per qualsiasi potenza superiore a 2. "
Al topo basta poco per fare due più due; numeri di tre cifre.. uno dei due deve essere la combinazione! E si mette subito al lavoro.. ma questa volta servono carta e penna. Il topo pensa: ma in fondo io posso limitarmi a trovare i due numeri nel primo caso, quello del quadrato.
Dopo svariati calcoli il topo trova la combinazione. Adesso non gli basta che vivere.. felice e contento!
- Limitiamoci per ora a dimostrarlo nel caso del quadrato. A scanso di equivoci ripeto ancora la domanda: cerchiamo dei numeri (xyz), con x<>0 tali che
=ab..xyz; xyz rappresenta la notazione posizionale in base dieci di un certo numero; x,y,z sono dunque le cifre. Quali sono questi numeri? Che calcoli fa il Topo-logico?
- Per chi vuole cimentarsi ulteriormente, come si fa ad estendere tale risultato nel caso generico di un esponente qualsiasi? E' vero che gli stessi numeri soddisfano alla
?
31 commenti
alla fine i numeri hanno sempre un fascino particolare. Come diceva Gauss:
" la matematica è la regina delle scienze" e la teoria dei numeri é la regina della matematica"
dimenticavo o forse no.. Nel testo si intravede che il topo ha solo carta e penna, non computer o calcolatrici. in ogni caso per risolvere il caso in cui l esponente vale n non basta neppure la scimmia del paradosso di Borel in quanto n diventa infinito
Limitatamente alla prima domanda, se il numero xyz , compreso tra 100 e 999 , elevato al quadrato, deve darmi un numero ab..xyz, allora significa che la differenza ( xyz^2 - xyz ) deve essere divisibile per 1000. Infatti , essendo le ultime tre cifre del numero elevato al quadrato uguali alle tre cifre del numero di partenza, facendo la differenza resterebbero solo le centinaia di migliaia (a) e/o le decine di migliaia (b) e le migliaia (c), tutte quantità divisibili per 1000, appunto. Quindi, deve essere nullo il resto della divisione ( xyz^2 - xyz ) / 1000.
Potrei quindi cercare i numeri in questione iterando la divisione
(n^2 - n)/1000 per n da 100 a 999, verificando ogni volta se il resto della divisione è nullo oppure no. Però sarebbero 1000 divisioni da fare con carta e penna...
A quel punto penserei piuttosto alle proprietà dei numeri automorfi ... ma non so se esse sono note al Topo-logico, quindi invocabili.
Con un semplice ragionamento e 6 facili moltiplicazioni si trova il primo numero che è 625.
Il suo quadrato è. 390625.
Con un semplice ragionamento e 3 moltiplicazioni si trova che il secondo numero è 376, il cui quadrato vale 141376.
Ambedue i numeri si possono trovare senza eseguire moltiplicazioni ma solo estendendo il ragionamento.
Fatemi iniziare con un ragionamento semplicissimo (forse utilizzando le moltiplicazione alla "cinese" o alla "giapponese" sarebbe anche meglio)
xyz xyz =
----------
........ z2
....... --
Mi fermo alle unità del quadrato, eseguendo le moltiplicazioni come si faceva una volta, mettendo in colonna...
Beh... è subito ovvio che z (numero intero diverso da zero, per adesso) deve avere un quadrato in cui le unità sono uguali a z...
Ne segue che z può essere solo 1, 5, 6... dato che 1 x 1 = 1, 5x5 = 25 e 6x6 = 36
Ovviamente, qualsiasi altra potenza di 6 deve finire per 6 e così per 5 e per 1...
Pensateci e passate al termine delle decine, conoscendo ormai le unità...
può citare qualsiasi cosa Arturo, basta che spieghi cos'è.
Buon giorno amici, sto per mettermi in auto con la famigliola, alla volta della suocera a 250 km di sitanza. Al volo: i numeri automorfi sono appunto wuelli che compaiono pari pari nel loro quadrato. 5 e 6 sono sutomorfi. Il bello e' che esiste una relazione tra i numeri automorfi , per cui sapendone uno si ricava l'altro: la somma dei numeri automorfi di k cifre e' pari a 10^k +1. Nel nostro caso 1001. Inoltre, il problema fice gia che sono solo 2, per cui basta ttovarne uno. Ancora, per trovare quelli compresi tra 200 e 999 basta partire da quelli a una sola cifra, come spiegava Vincenzo. Ma ora mi tocca partire per la suocera. Spiegherai tutto tu come si deve, Umberto. Simpaticissimo questo Topo-logico.
io l'ho risolto in altro modo. Sono contento che se ne trovi un altro. Lascio a voi concludere, tanto c'è tempo.
Scrivi pure il tuo ragionamento Maurizio, tanto qui mi sembra che stiamo prendendo tutti strade diverse.
il ragionamento che ho seguito è sostanzialmente quello citato anche da Enzo, ossia moltiplico incolonnando i parziali e sfruttando le relazioni che si evidenziano.
................ x y z
................ x y z
__________________________
................ zx zy z^2
xy y^2 zy
x^2 xy zx
___________________________
Le prime due colonne non mi interessano, considero solo le tre colonne di destra ( in rosso)
Inizio con la prima a sinistra , che mi dice che calcolando z^2 e analizzando il resto della divisione per 10 devo ottenere z.
Questo avviene solo con 1 , 5 , 6 i cui quadrati sono rispettivamente 1 , 25 , 36.
Se assumo z = 1 , ho immediatamente 2zy = 2 y, che deve essere = y . Cosa possibile solo con y=0
Inoltre, dati z=1 e y=0, ottengo 2x = x, che implica x = 0.
Ma il numero 001 è inferiore a 100 quindi lo scarto.
Passo a considerare l'alternativa z=5. Ottengo z^2 = 25 che implica un riporto 2 che va a sommarsi a 2*5y nella colonna a sinistra
Pertanto : resto ((2+ 10y)/10 ) = y Il che significa y=2
Ora so che il primo numero di 3 cifre termina con 25 e mi basterebbe eseguire poche moltiplicazioni per trovarlo. Tuttavia posso proseguire nel mio ragionamento e considerare la successiva colonna a sinistr. :
Sommo al riporto 2 il valore 2zx e il valore y^2 . Pertanto, resto (( 2+10x + 4)/10)=x Da cui x=6
il primo numero è 625.
Ora passo al secondo numero.
Sappiamo che z=6. per quanto riguarda la y devo analizzare: resto((3+12y)/10)=y
il primo valore di y che soddisfa è y=7, quindi il numero di tre cifre termina per 76
Anche un questo caso mi basterebbe eseguire poche moltiplicazioni per trovarlo, ma proseguo con il ragionamento di prima.
Sommo al riporto 8 il valore 2zx e il valore y^2. Pertanto, resto ((8+ 12x + 49)/10) = x , che si riduce a dover analizzare: resto ((7+12x)/10)=x , da cui si deduce x=3.
il secondo numero è 376.
ok Maurizio, grazie. aspettiamo gli altri. Nel contempo, possiamo cominciare a pensare alla seconda parte del quiz. Se provate con il numero 376, vi accorgerete che anche le potenze successive(3,4,5..) terminano con 376. Chiaramente questo non costituisce una dimostrazione ; che dire per la potenza n-esima?
Anche io mi baso sul ragionamento di Enzo, facendo poi lavorare solo le potenze di 5, ottenendo l'altro numero per differenza;
questo è quello che ho ottenuto empiricamente, che non è dimostrazione, ma mostra solamente come si sono comportati i numeri:
intuitivamente mi sembra ovvio... se esiste un numero il cui quadrato finisce con le tre ultime cifre uguali, vuol dire che ogni volta che moltiplico due numeri che finiscono per 376 (ad esempio) devono finire con le stesse tre cifre. Fare il quadrato è moltiplicare un numero per se stesso e se le ultime tre cifre non cambiano, non cambieranno mai ogni volta che lo moltiplico per lo stesso numero. Quelle che interessano sono sempre e soltanto le ultime tre cifre dei numeri che si moltiplicano tra di loro... il resto non importa...
Se vale per
376 x 376... deve valere per qualsiasi numero che finisce con 376
376 x 376 = a......e376
a.....e376 x 376 = f....p376
mi spiego meglio...
se xyz x xyz = .....xyz (dimostrato)
qualsiasi ulteriore moltiplicazione per xyz DEVE dare un numero che termina con xyz, dato che le ultime tre cifre di qualsiasi moltiplicazione si determinano attraverso le ultime tre cifre dei singoli fattori, che sono sempre xyz.
grazie Andy
quello che dici è. Senz'altro vero Vincenzo.. Ma non so se tutti lo vedano senza entrare nei dettagli.
beh... è sempre lo stessa schema utilizzato anche da Maurizio
............ x y z • x y z =
----------------------------------
questa zx zy z2
parte sempre y2 yz ---
uguale xz ---
se valeva .... xyz nel primo caso, deve valere sempre... lo schema è sempre lo stesso.
ok. Io ho seguito un approccio un po' diverso, simile al primo commento di Arturo. Comunque non so quale sia più immediato.
comunque mi piacerebbe sentire qualche altra opnione , per esempio ..non faccio nomi..
Al momento non vedo una spiegazione alternativa a quella di Enzo che coincide con quello che penso anche io.
Mi sembra convincente l'idea che ripetendo la medesima struttura dei calcoli sia inevitabile ottenere lo stesso risultato, un po' come succede con i numeri periodici rappresentati in forma di frazione. Alla fine il ciclo si ripete all'infinito perché nel calcolo entrano in gioco sempre le medesime cifre nella medesima sequenza.
Quindi se, moltiplicando un numero per se stesso, lo ritrovo in coda al risultato, ripetendo l'operazione per un numero di volte grande a piacere, troverò sempre in coda lo stesso numero.
Le vostre soluzioni sono certamente valide. Cercavo di capire se qualcuno ne ha altre in mente.
la butto lì senza alcuna pretesa (devo andare a pulire dietro casa...):
Ma sono piccoli lampi... senza fondamento... Vado a lavorare...
Non cambia il succo, ma potrei scrivere il numero di partenza come
100 x + 10 y + z = xyz
e poi fare i suo quadrato:
10000 x2 + 100 y2 + z2 + 2000 xy + 200 xz+ 20 yz = abc xyz (deve essere un numero di 5 o 6 cifre).
10000 x2 + 2000 xy + 100(y2+ 2xz) + 10(2 yz) + x2 = abcxyz
A noi interessano solo dalle centinaia in giù, ossia
100(y2+ 2xz) + 10(2 yz) + x2 = xyz
e si ricade nel caso illustrato da Mau...
ops, non ho messo il 2 come esponente, ma si capisce lo stesso...
ok grazie Vincenzo
Dico anche la mia. Non ho seguito tutti commenti e potrei dire cose già dette.
La condizione del quiz la posso scrivere in questo modo. La variabili di seguito sono tutte intere positive
da questa espressione sono riuscito a ricavare poco, quindi ho dovuto sostituire N con la sua espressione decimale.
Dalla quale ricavo 3 relazioni considerando i riporti
Dalla prima si vede che z o (z-1) devono essere multipli di 5.
Quindi z=5 o z=6, nel primo caso n=2 e nel secondo n=3.
Sostituisco queste due prime soluzioni nella seconda relazione ed ottengo
Dalla prima capisco che 9 y deve terminare per 8 dalla seconda che 11 y deve terminare per 7.
Quindi abbiamo due possibilità:
z=5 y=2 m=2 o z=6 y=7 m=8
li sostituisco nella 3a relazione e ottengo
Dalla prima capisco che 9 x deve terminare per 4 dalla seconda che 11 x deve terminare per 3.
Quindi abbiamo che nel primo caso x=6 e nel secondo caso x=3.
Il nostro numero potrà essere o 625 o 376
grazie Fabrizio, mi sembra una valida alternativa.
La seconda domanda l'affronterei in questo modo. Le variabili di seguito sono interi positivi.
L'ipotesi è che N sia un numero positivo minore di 1000 che soddisfa la relazione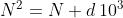
. Da questa ipotesi vogliamo dimostrare che soddisfa anche la relazione più generale 
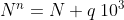per qualsiasi n.
Per dimostre questa ultima affermazione passerei per la dimostrazione che se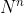
ha N come prime 3 cifre, anche 
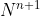è un numero che ha come prime tre cifre N.
Quindi se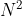
inizia per N, inizia per N anche 
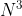e a seguire 
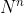qualsiasi sia n.
ho visto adesso. Ok Fabrizio.