Un Quiz... irrazionale!
Un quiz un po'.. fuori dal comune, e forse veramente difficile. Non so giudicare tale difficoltà. Di solito i quiz hanno una soluzione, e qualche diverso metodo per arrivarci. Qui no.. secondo me le soluzioni sono veramente tante.. oserei dire .. infinite! E' un quiz infatti che lascia molta libertà di pensiero e fantasia matematica! La domanda è molto semplice:
Siano p, q due numeri reali irrazionali. Consideriamo il numero reale:
E'' possibile che x sia un numero irrazionale? E' possibile che x sia un numero razionale?
PS: La domanda può sembrare ambigua.. in realtà non lo è. In ogni caso sono qui per ulteriori chiarimenti.






53 commenti
attenzione Però Fabrizio che p, q sono due numeri irrazionali.qui ne vedo tre; quali sarebbero p e q?
scusa Umberto, non capisco la deconda domanda perfettamente identica alla prima...
Se il numero tra parentesi è irrazionale, allora p sarebbe il numero tra parentesi e q la radice di 2. Non so dimostrare che il numero tra parentesi è irrazionale. Comunque, se non lo fosse sarebbe esso stesso un esempio di x razionale con p e q uguali a radice di 2.
Quindi all'interno della espressione c'è un esempio di x razionale.
infatti adesso correggo. Razionale non irrazionale uno dei due.grazie mille
legandomi a Fabrizio...
(√2)(√2)
è del tipo pq con p e q irrazionali. Il risultato è ancora irrazionale, direi...
Ok Fabrizio, per il razionale potrebbe andare bene, se scritto in un modo più completo(comprensibile a tutti). In pratica mi piacerebbe che tu riassumesti quanto affermato.
Vincenzo: non penso si possa dire a priori che (√2)(√2)
si irrazionale
però anche qui può esserlo o non esserlo comporta..
le due domande si escludono... se non vale l'una deve valere sicuramente l'altra... è questo il succo?
no non si escludono in generale. Chiaramente per determinati valori si
Come suggerito da Umberto provo a scrivere in modo più esteso la mia risposta affermativa alla domanda "è possibile che x sia razionale?"
Considero l'espressione^\sqrt{2}) . Questa espressione è uguale a 2, cioé da come risultato un razionale.
. Questa espressione è uguale a 2, cioé da come risultato un razionale.
Infatti^{\sqrt{2}}&space;=\sqrt{2}^2=2)
Come prima ipotesi si può identificare p con) e q con
e q con  .
.
Il quiz però richiede che p e q siano irrazionali. Ora è certamente irrazionale, ma
è certamente irrazionale, ma ) possiamo dimostare che sia irrazionale? Io, almeno in questo momento, non saprei farlo. Però ai fini della risposta alla domanda del quiz questa ignoranza può essere aggirata. Vediamo come.
possiamo dimostare che sia irrazionale? Io, almeno in questo momento, non saprei farlo. Però ai fini della risposta alla domanda del quiz questa ignoranza può essere aggirata. Vediamo come.
I casi possono essere 2:) è irrazionale o è razionale.
è irrazionale o è razionale.
Se fosse irrazionale allora la prima ipotesi fatta sopra,\;\;e\;\;q=\sqrt{2}) , ci permetterebbe di rispondere affermativamente alla domanda "è possibile che x sia razionale?".
, ci permetterebbe di rispondere affermativamente alla domanda "è possibile che x sia razionale?".
Se fosse razionale allora comunque si potrebbe rispondere affermativamente alla stessa domanda con\;\;e\;\;q=\sqrt{2}) , che sono entrambe certamente irrazionali.
, che sono entrambe certamente irrazionali.
Comunque vada, l'espressione^{\sqrt{2}}&space;=2) ci permette di dimostrare che esiste almeno un
ci permette di dimostrare che esiste almeno un 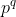 , con p e q irrazionali, che da un risultato razionale.
, con p e q irrazionali, che da un risultato razionale.
perfetto Fabrizio, non è. Un ragionamento da poco.
adesso penso si capisca perché non è. Semplice scrivere il testo di questo quiz. Nella risposta di Fabrizio più che trovare due valori si inventa un metodo quasi alternativo . Bisogna adesso trovare un caso per l irrazionalità. Dopo di che.. Il quiz potrebbe continuare all infinito. Si possono trovare infinite soluzioni.Quindi mi aspetto altre soluzioni. Un piccolo suggerimento.. Pensate ai logaritmi.
eiπ = -1
si però saremmo nei reali..
hai ragione, hai ragione... me ne ero dimenticato
mi piacerebbe risolvere almeno un caso irrazionale..il quiz lo trovate difficile o poco interessante?
come dicevi tu, si potrebbe utilizzare un logaritmo che può essere irrazionale anche se base ed esponente sono numeri interi... ma, sinceramente, lo trovo un esercizio un po' fine a se stesso... e devo continuare a pensare all'evoluzione stellare che è un po' che aspetta, così come la storia del pigreco (prima ancora che si dimostri irrazionale e trascendente...)... Ovviamente, questa è solo la mia personale posizione...
per me i quiz devono essere fini a se stessi; sono un gioco, un divertimento. Chiaramente se un gioco riesce subito risulta divertente, altrimenti no. Comunque non pensare che sia banale, vedrai a che ragionamenti astratti ed eleganti può portare nella soluzione, mentre in ogni caso può anche essere risolto in modo molto semplice. Comunque la tua posizione influenzerà anche troppo.
caro Umberto,
io cerco sempre (o quasi) di proporre quiz che permettano poi di affrontare un problema concreto. Non per niente, molti di essi sono finiti nell'archivio come approfondimenti. La caduta libera è un argomento che va ben al di là del puro divertimento. Spesso, però, è anche giusto divertire e basta... e quindi fai bene a proporli, ma non dire che io influenzo la partecipazione... A volte ho tempo di seguirli a volte no... Ognuno ha i suoi tempi e i suoi interessi. Non penso proprio che esprimere una mia particolare condizione attuale vincoli le scelte dei lettori completamente liberi di seguire la strada che preferiscono. Il bello del Circolo (penso) sia quello di fornire pane per tutti i tipi di denti...
non per la tua partecipazione, ma per come l hai definito. Comunque io ho sempre fatto quiz con risvolti didattico. Dalle curve ellittiche ai grafi, ma evidentemente non andavano bene nemmeno quello. Sei tu che avevi detto di scendere di livello. Permetterai che i quiz per arrivare alla dimostrazione della irrazionalità di p-greco erano più facili di quello che abbiamo visto ieri. Che fra l altro come ti ho via detto non può essere considerato un quiz, essendo noto in letteratura.per me ci stava meglio un articolo.
Penso che nessuno sia in grado di presentare qualcosa che non sia presente il letteratura. Non vedo niente di male a proporre un quiz che si trasformi poi in un articolo didattico. L'hai fatto anche tu molto recentemente, portando avanti un discorso attraverso una serie di quiz. Un metodo sicuramente interessante.
Io non ho fatto altro che dire: argomento un po' fine a se stesso, ma non per questo l'ho sminuito. Anzi, ai matematici puri piacerà un sacco...
Ricordiamoci, poi, che qualsiasi articolo o quiz è proposto per i lettori e non per noi stessi. Questo è il Circolo...
Non ho mai contestato la tua non partecipazione a molti quiz geometrici e/o relativistici... E' giusto che ognuno scelga ciò che lo interessa di più. Siamo liberi e soprattutto dobbiamo cercare di interessare i lettori e farli divertire pensando. Io non ho nessun interesse a mostrare me stesso e le mie capacità. Ben vengano, perciò, anche argomenti di dominio pubblico, ma poco conosciuti... Tant'è che la soluzione più facile della caduta della Terra è stata toccata per ultima... ma ha insegnato qualcosa a tutti, perfino a Fabrizio, che come preparazione è decisamente di alto livello (la sua lagrangiana e la diseguaglianza di Bell ne sono una prova inconfutabile...).
non sto contestando niente.E vero che i quiz sono destinati si lettori, ma a parte noi non partecipa mai nessuno. Siamo solo quattro o cinque.. Se nessuno risponde non so nemmeno se valga proporli. Tanto vale presentarli con già la soluzione. Per quanto riguarda i polinomi di Niven puoi cercare dive vuoi. La dimostrazione é stata elaborata quasi in modo autonomo, semplificando quelle esistenti
che i lettori non rispondano è cosa ormai risaputa, ma ciò non vuol dire che non siano letti e che qualcuno non riesca anche a risolverli. Il numero di lettori è sempre molto alto e significa che molti ci tornano su varie volte...
E poi, possono servire per aprire un discorso più ampio e di maggiore approfondimento.
Io penso che continuerò, cercando di attirare l'interesse su fenomeni o processi che aprano nuovi sviluppi, come avevo fatto a suo tempo con la RR, ad esempio...
bisognerebbe riuscire a far superare lo scoglio della timidezza. Se qualcuno come dici tu risolve e non dice niente é un peccato
Io temo che sia proprio così... la paura di fare brutta figura è piuttosto comune. Forse dovremmo dare il risultato in modo che ci sia una conferma... ma sovente il risultato fa capire tutta la questione...
E anche la presentazione tipo: "dimostrare che vale una certa relazione" crea il problema di aver risolto in modo non abbastanza professionale...
Qui non siamo in un forum o in facebook dove tutti sparano a zero. La qualità genera anche molta paura di uscire allo scoperto. Meglio un Leandro, un Andy (ma anche qualche altro) ogni tanto che non una schiera di creatori di nuove teorie o di mordi e fuggi. Umiltà, innanzitutto, e tanta voglia di far conoscere a chi vuole VERAMENTE usare la testa. Senza far nomi, ricordo qualcuno che combatteva contro le derivate e che ora potrebbe dare lezioni di relatività a molti professionisti (e non solo quella...).
Forza e coraggio Umbertino!!!!
sbaglio a dire che il logaritmo c in base irrazionale a dell'argomento irrazionale b , è anch'esso irrazionale? In questo caso b = ac vede tre numeri irrazionali... boh?
come non detto: il logaritmo in base e di e è uguale a 1, razionale....
ok
Non sono certo che si possa dare questa impostazione, ma la propongo comunque:
Pongo p = q. Allora l'espressione da considerare diventa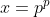
Se ora al posto di p scrivo il valore irrazionale "e" il risultato del calcolo dovrà essere un numero irrazionale, ottenuto dalla somma di termini ciascuno dei quali è irrazionale.
non ho capito bene quello sviluppo, ma in ogni caso non è sempre vero che la somma di numeri irrazionali sia un numero irrazionale;
é anche vero che se non è irrazionale allora é irrazionale.. Ma potresti spiegare meglio quello sviluppo?
Cercando il grafico di x^x a questa pagina ho trovato lo sviluppo in serie di Puiseux relativo. Sembra che Newton ci abbia pensato con un anticipo di 200 anni. Ho comunque il dubbio che questo sviluppo abbia valore solo localmente, in prossimità di x=0.
Che ne pensi?
penso che dovrei vedere.ma meglio non disperderci e ragionare sul quiz
ma&space;=&space;\pi) =>
=> 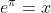 x non è senz'altro irrazionale?
x non è senz'altro irrazionale?
ciao Andy il problema è proprio questo; se non riusciamo a confrontarlo con un numero che sappiamo sia irrazionale non possiamo dire niente. Bisogna cercare una uguaglianza con un numero noto.
Ciao Umberto,
una semplice ipotesi:
se si pone) con
con  reale irrazionale positivo, si ha che:
reale irrazionale positivo, si ha che:
allora per ogni reale razionale
reale razionale 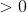 e
e 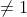 esistono almeno un numero
esistono almeno un numero  e un numero
e un numero  reali irrazionali tali che sia soddisfatta l'equazione
reali irrazionali tali che sia soddisfatta l'equazione 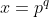 ;
;
e per ogni reale irrazionale
reale irrazionale 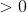 e
e 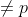 esistono almeno un numero
esistono almeno un numero  e un numero
e un numero  reali irrazionali tali che sia soddisfatta l'equazione
reali irrazionali tali che sia soddisfatta l'equazione 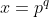
Io sono convinto che ee sia irrazionale... basta provarlo...
Andy,premesso che l'approccio mi piace, siamo su una via buona ma ancora non ci siamo.
Tu prendi un p irrazionale ; poi consideri) ; ma purtroppo non possiamo dire che q sia sempre irrazionale. per esempio, se p=
; ma purtroppo non possiamo dire che q sia sempre irrazionale. per esempio, se p=  , x=2 (razionale), q=2, che è razionale. Dovresti cercare dei numeri per cui sia vero quello che affermi in generale.
, x=2 (razionale), q=2, che è razionale. Dovresti cercare dei numeri per cui sia vero quello che affermi in generale.
Ti consiglio poi di lasciar perdere la generalità; nessuno può farlo. Bisogna scovare dei numeri di cui siamo sicuri se siano o no irrazionali. Fabrizio ha manipolato , noi possiamo cercarne degli altri. Lavorare con i logaritmi può essere più semplice per trovare la soluzione, visto che cerchiamo certe potenze. Faccio una domanda, aperta non solo a te :
, noi possiamo cercarne degli altri. Lavorare con i logaritmi può essere più semplice per trovare la soluzione, visto che cerchiamo certe potenze. Faccio una domanda, aperta non solo a te :
log 2 3 è un numero razionale?
Per rispondere all'ultima domanda di Umberto provo ad utilizzare un ragionamento per assurdo.
Supponimo che il valore del log sia un razionale, allora potrei scrivere che sviluppo
che sviluppo
Che evidentemente non può essere con m ed n interi. Il ragionamento si può fare in modo equivalente con le radici.
Quindi in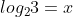 , che equivale a
, che equivale a 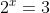 , x dovrebbe essere irrazionale. Ma bisogna far diventare irrazionali anche gli altri due. Facendo la radice quadrata si dovrebbe raggiunge lo scopo.
, x dovrebbe essere irrazionale. Ma bisogna far diventare irrazionali anche gli altri due. Facendo la radice quadrata si dovrebbe raggiunge lo scopo.
é proprio cosi. E par trovare un valore razionale sempre usando quel logoritmo?
Mi sembra anche generalizzabile a qualsiasi coppia di numeri primi al posto di 2 e 3.
era il discorso delle infinite soluzioni..
Parlando ancora di risultati irrazionali....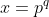
ponendo p=e (irrazionale) e) (irrazionale) ottengo
(irrazionale) ottengo }=\pi) irrazionale.
irrazionale.
Sembra un gioco di parole, una tautologia, come dire che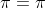 , tuttavia anche se le due scritture sono equivalenti da un punto di vista formale abbiamo tre numeri irrazionali che entrano in relazione come prescritto dalla formula.
, tuttavia anche se le due scritture sono equivalenti da un punto di vista formale abbiamo tre numeri irrazionali che entrano in relazione come prescritto dalla formula.
Per trovare un valore razionale partendo da=\sqrt&space;3) occorre far sparire la radice a destra, cioè elevarla al quadrato.
occorre far sparire la radice a destra, cioè elevarla al quadrato.
é sempre il solito problema Maurizio. Non si sa se ln(p greco) sia irrazionale malgrado sembra evidente di si
proprio così Fabrizio. Mancherebbe da dimostrare il caso di irrazionalità della tua prima risposta
Si può provare a dimostrare che) è irrazionale? Seguirei la stessa logica usata in precedenza da Fabrizio:
è irrazionale? Seguirei la stessa logica usata in precedenza da Fabrizio:
suppongo che sia razionale, allora posso scrivere:=\frac{m}{n}) con m ed n interi , ne consegue che
con m ed n interi , ne consegue che =&space;m*ln(e)) e quindi
e quindi
Mi sembra che l'uguaglianza dei due termini si possa avere solo con n = m = 0 e venga così negata l'ipotesi iniziale di poter esprimere questo logaritmo come frazione.
sembra proprio di si.
Quindi x razionale è possibile. Per inciso ciò implica che una potenza irrazionale di irrazionale può essere un numero intero.
scusa Leandro ma quel p=e? Quello é logaritmo naturale penso.
Sì p=e.
Migliore dimostrazione:
ma il logaritmo naturale di un razionale non è mai razionale.
Infatti se fosse
si avrebbe
cioè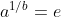
cioè e sarebbe soluzione di una equazione polinomiale, ma sappiamo che e è trascendente , quindi....
e questa da dove l hai tirata fuori? Grazie Leandro la guardo attentamente.
ok possiamo chiudere qui, anche se chi vuole può ancora aggiungere dei commenti Sembra che Leandro abbia chiuso in bellezza, agganciandosi addirittura al mio ultimo articolo, e facendo notare una coda che onestamente non sapevo. Comunque ne parleremo nella soluzione. Notate quante sfaccettature può avere un semplice dilemma. E non è ancora finita.