Questo articolo è stato inserito in "Il moto dei pianeti secondo Feynman", al quale si rimanda per una trattazione completa dell'argomento

 

Non stupitevi dell'unico asterisco inserito nel titolo. L'articolo, in realtà, non va oltre e ciò che è necessario sapere per poterlo seguire senza problemi sono i  primi due principi della dinamica di Newton e il calcolo dell'area di un triangolo qualsiasi. I concetti sono quelli usati da Feynman anche se  ho cercato di renderli ancora più ... elementari, attraverso molte figure ed esempi.

Come ulteriore aiuto, prima di iniziare, ripeto i primi due principi di Newton utilizzando proprio le sue parole (tradotte):

1. Ciascun corpo persevera nel suo stato di quiete o di moto rettilineo uniforme, salvo che sia costretto a mutare quello stato da forze applicate ad esso.
2. Il cambiamento di moto è proporzionale alla forza motrice risultante applicata, ed avviene lungo la linea retta secondo la quale la forza stessa è stata esercitata. Questo moto, se il corpo era già mosso, viene aggiunto al moto di quello.

Bene, rinfrescata un po' la memoria, vediamo di determinare la seconda legge di Keplero senza alcuna equazione differenziale o calcolo complicato.

Sia O un corpo che si muove con velocità costante lungo una linea retta come indicato dal Primo Principio. Essendo la velocità costante, esso compirà tragitti uguali in tempi uguali, come mostrato in Fig. 7.

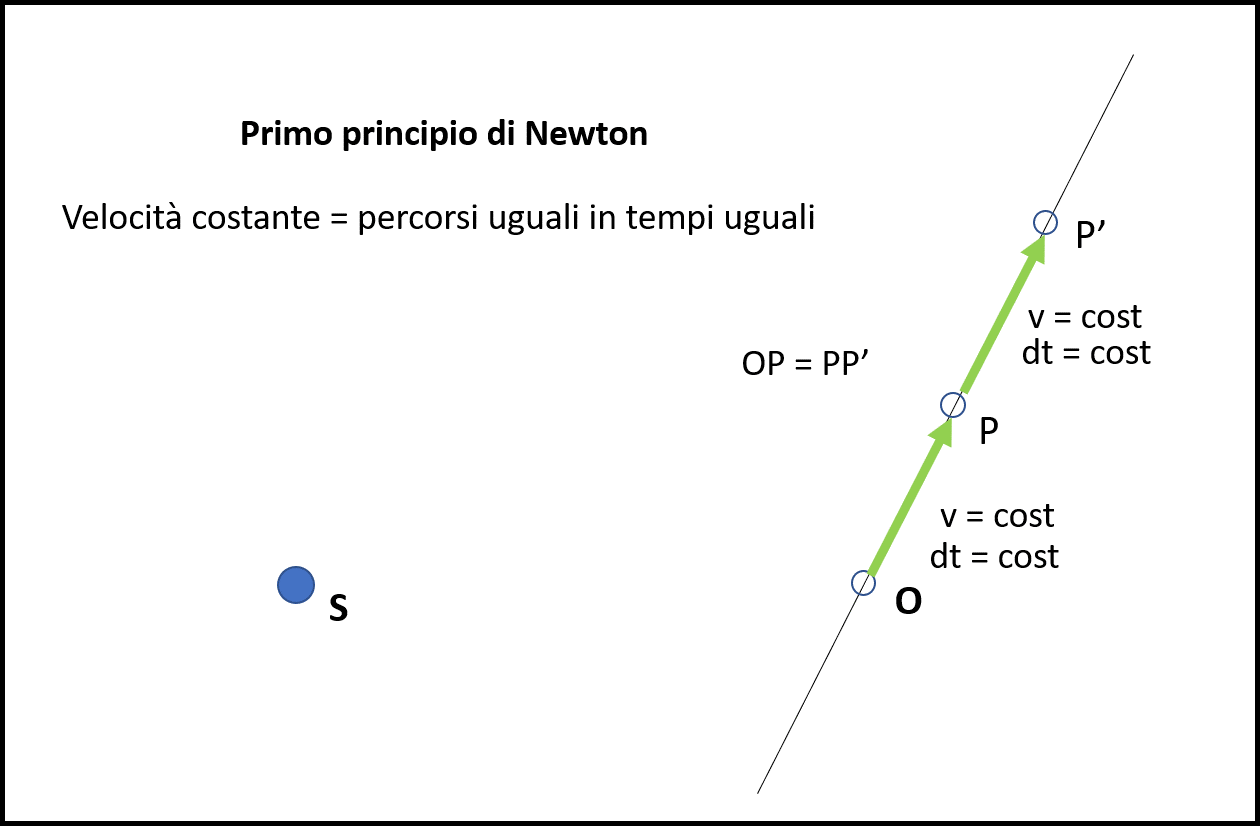
In un certo tempo dt il corpo O si porta in P e poi, sempre nello stesso tempo, si porta in P'. Essendo la velocità costante non abbiamo problemi a considerare tempi anche molto lunghi. In seguito, però, continueremo a usare triangoli di dimensioni considerevoli, pensando che il tempo trascorso sia molto piccolo così come  il tragitto percorso dal corpo celeste. La possibilità di ridurre a piacere le dimensioni di ogni tratto percorso ci garantisce che la correttezza delle conclusioni.

A sinistra del nostro corpo (che possiamo anche considerare un pianeta) si vede il Sole S, che immaginiamo, però, dormiente del tutto e incapace perfino di influenzare con la sua massa il moto del pianeta. Lo utilizziamo, per adesso, solo come origine dei segmenti che andiamo a tracciare. In poche parole, congiungiamo S con O, con P e con P'.  Otteniamo i due triangoli SOP e SPP' di Fig. 8.

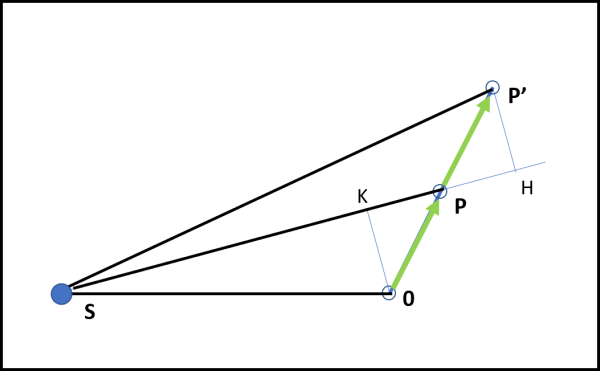
Ci vuole un attimo (Fig. a concludere che le loro aree sono uguali. Essi hanno la stessa base SP e la stessa altezza OK = P'H. Le due altezze sono uguali, in quanto cateti di due triangoli rettangoli uguali (PKO e P'HP), dato che hanno la stessa ipotenusa (tragitto compiuto dal pianeta nel tempo dt) e gli angoli in P uguali perché opposti al vertice. Ne segue che i due triangoli hanno la stessa area.

Lo stesso procedimento  può essere usato per i tratti P'P'' e P''P''' di Fig. 9.

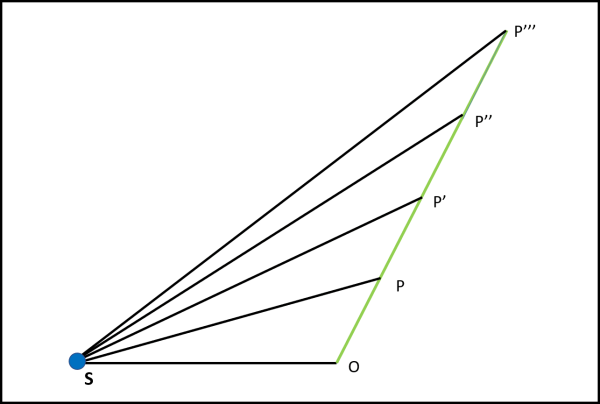
Il che ci permette di concludere che, rispetto a un punto fisso S, le aree spazzate dal pianeta in tempi uguali, durante il suo moto rettilineo uniforme, sono sempre uguali.

In qualche modo, abbiamo già dimostrato la seconda legge di Keplero che dice che le aree spazzate in tempi uguali dai pianeti attorno al Sole sono uguali. Beh... sarebbe vincere in modo troppo facile. L'esempio considerato finora considera un Sole del tutto ininfluente, anche se quanto trovato vale per qualsiasi posizione passata e futura del nostro pianeta che se ne va dritto per la sua strada. Parlando seriamente, possiamo concludere che, se il Sole non esercitasse alcuna forza, il solo primo principio della dinamica stabilirebbe che le aree spazzate dal pianeta (vagabondo) devono restare uguali.

Facciamo, allora entrare in gioco anche il secondo principio della dinamica. Il Sole si accende sotto tutti i punti di vista: non solo diventa rosso ma esercita una forza sul pianeta. Il secondo principio dice che tale forza implica uno spostamento del moto  nella direzione della forza agente che possiamo ipotizzare diretta verso il Sole.

F = ma = m dv/dt  = m ds /dt² ∝ ds           (il segno ∝ sta per "proporzionale a")

Tale forza deve dar luogo a un movimento diretto in quella direzione che deve essere sommato a quello preesistente, come mostrato in Fig. 10.

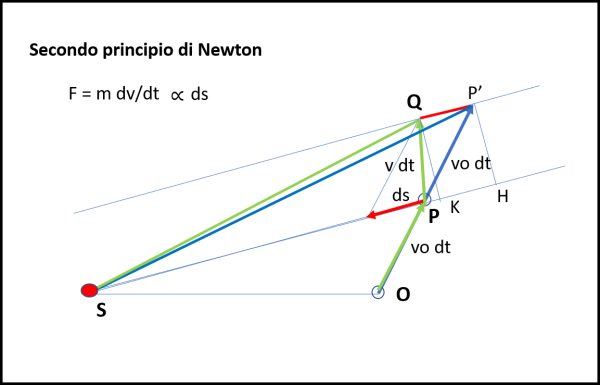
Lasciamo perciò tranquillo il nostro pianeta tra O e P, ma poi, in P applichiamogli la forza F diretta verso il Sole che da luogo a uno spostamento ds verso di lui, che si deve sommare a quello vo·dt che il corpo aveva nel suo moto rettilineo uniforme. In conclusione, dopo un intervallo di tempo dt (sempre lo stesso), il pianeta si è spostato di v·dt, ossia percorre  il segmento PQ. Non ci resta, adesso, che dimostrare che anche il triangolo SQP ha la stessa area del triangolo SP'P (a sua volta uguale, come appena dimostrato, a quella di SPO).

Si vede subito che i due triangoli hanno la stessa base SP, ma anche la stessa altezza QH = P'K, dato che QP' è parallela a SP per costruzione.

Facciamo molta attenzione a un fatto decisamente importante, illustrato in Fig. 11

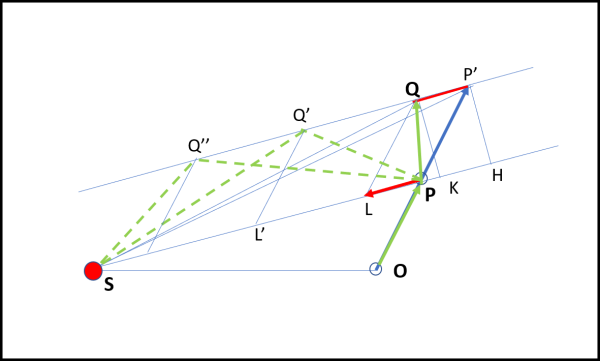
Dato che QP' è parallela a SP, possiamo considerare qualsiasi  deviazione PL, PL', PL''..., dovuta alla forza esercitata dal Sole. L'unica cosa che cambierebbe sarebbe il punto Q, che diventerebbe Q' , Q'', ecc. Ma i triangoli SQ'P, SQ''P, ... avrebbero sempre la stessa area di QSP. L'area spazzata dal pianeta sotto l'azione di una forza diretta verso il Sole, qualsiasi sia la sua intensità, resta sempre uguale, lavorando su intervalli di tempo uguali. O, se preferite: la forza che attrae il pianeta verso il Sole cambia la traiettoria, ma non il valore dell'area spazzata.

La costruzione fatta in Fig. 10 può essere applicata nuovamente al tratto successivo, come mostra la Fig. 12:

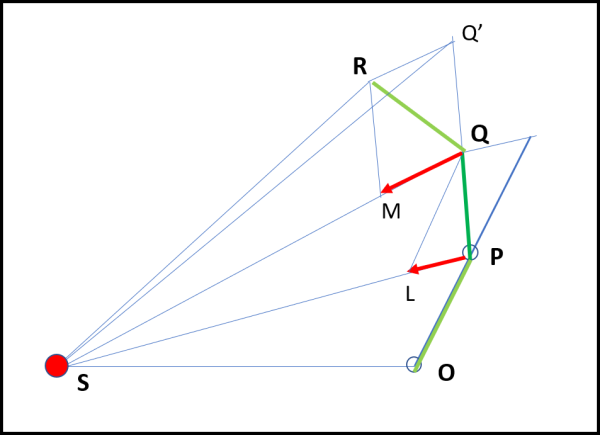
Il pianeta proseguirebbe verso Q', ma il Sole impone lo spostamento QM. Il segmento RQ' è parallelo a MQ e, come nel passo precedente, i triangoli SRQ e SQQ' hanno la stessa area. Ma SQQ' ha la stessa area di SPQ, dato che QQ' è uguale a PQ (la velocità resta costante se non ci fosse la forza del Sole). La faccenda si ripete pari pari ogni volta, assumendo sempre lo stesso intervallo di tempo dt. Come già accennato possiamo scegliere MQ di lunghezza qualsiasi.

Continuando in questo modo si può costruire l'intera traiettoria del pianeta attorno al Sole e si dimostra facilmente che tutte le aree spazzate in tempi uguali sono uguali, ossia vale la seconda legge di Keplero.

N.B.: segue un inserto un po' più difficile, ma molto utile

Si può anche dimostrare facilmente che questa conclusione equivale a dire che il momento angolare deve rimanere costante.

Usiamo la Fig. 13

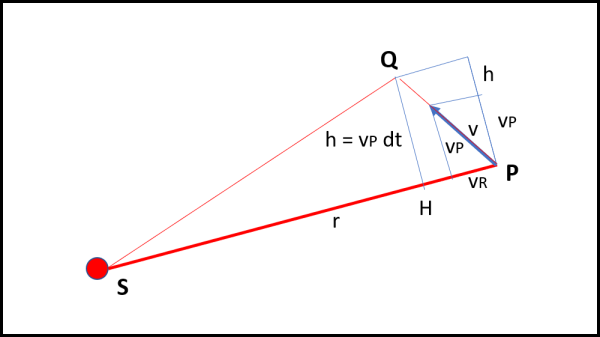
Il tragitto compiuto dal pianeta durante il tempo dt non è altro che v dt. Tuttavia v possiamo spezzarla in due componenti : v_P e v_R, la prima perpendicolare alla distanza r tra S e P,  la seconda  lungo la direzione SP. L'altezza  h è allora uguale a v_P dt.

Quanto vale l'area del triangolo "spazzata" dal pianeta?

A = 1/2 r h = 1/2 r v_P dt = costante           .... (1)    (come dimostrato precedentemente).

Quanto vale il momento angolare I ?

I = mv ∧ r

Siamo di fronte a un prodotto vettoriale e il risultato è un vettore. Possiamo, però, dividere la quantità di moto mv nelle sue due componenti:

mv = mv_P + mv_R

Vale ancora:

I = mv ∧ r = mv_P ∧ r + mv_R ∧ r

Ricordiamo che il momento angolare di un vettore diretto verso il centro S è nullo (c'è di messo un seno),  Quindi resta soltanto:

I = m v_P ∧ r

il cui modulo è

I = m v_P r                                      .... (2)    (il seno dell'angolo è uguale a 1)

Ma dalla (1) abbiamo che 

v_P r = 2A/dt

Sostituiamolo nella (2) e otteniamo:

I = m 2A/dt = costante.

Abbiamo dimostrato in modo banalissimo che la frase "spazzare aree uguali in tempi uguali" equivale perfettamente a dire che  "il momento angolare del pianeta durante il suo moto attorno al Sole rimane costante". Grande Feynman!!

Fine inserto "difficile" (non certo per chi conosce il momento angolare...)

Torniamo a noi e ai nostri triangoli.

Abbiamo dimostrato la seconda legge di Keplero utilizzando solo i primi due principi della dinamica, ma non possiamo certo essere soddisfatti. Infatti, la legge vale qualsiasi sia l'intensità della deviazione imposta dalla forza diretta verso il Sole. In altre parole, cambiandola a piacere, potremmo ottenere qualsiasi percorso, anche il più bizzarro e caotico.

Senza esagerare con forze ballerine, potremmo decidere che la forza rimanga costante qualsiasi sia la distanza del pianeta . Non è difficile costruire la traiettoria che ne segue e che non si chiude mai, come mostrato nella sua costruzione riportata in Fig. 14 (da sinistra verso destra).

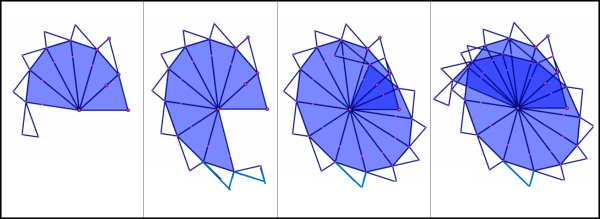
Insomma, per potere decidere qual è la vera traiettoria non basta aver trovato la seconda legge di Keplero. Bisogna dare la definizione della forza che agisce sul pianeta. In altre parole, bisogna accettarla o ricavarla utilizzando la terza legge di Keplero. Cosa che faremo la prossima volta...