Categorie: Meccanica Celeste
Tags: diagramma orbitale diagramma velocità Feynman Keplero moto pianeti attorno al Sole Newton
Scritto da: Vincenzo Zappalà
Commenti:0
Keplero e Newton rivisitati da Feynman. 3 : La forza di gravità **
Questo articolo è stato inserito in "Il moto dei pianeti secondo Feynman", al quale si rimanda per una trattazione completa dell'argomento
La volta scorsa eravamo rimasti "in panne" dato che, pur avendo ricavato la seconda legge di Keplero, ben poco si poteva dire sulla traiettoria di un pianeta attorno al Sole. Per fare questo passo in avanti è necessario conoscere come agisce la forza esercitata dal Sole, in funzione della distanza del pianeta. Ho aggiunto un asterisco solo perché bisogna capire molto bene la costruzione elementare di un nuovo diagramma...
Sicuramente la forza deve essere valida per tutte le orbite fisicamente possibili. Scegliamone, allora una molto particolare che sia oltremodo realistica, anche se decisamente semplice.
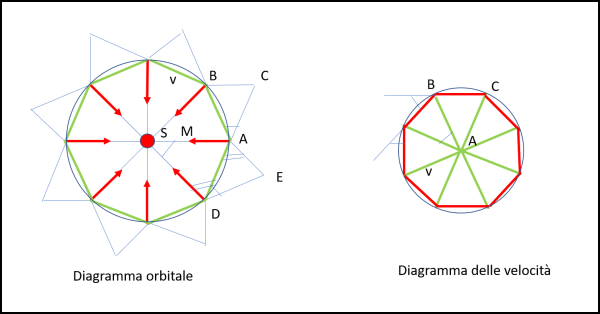
Cominciamo a costruire la nostra traiettoria con il metodo usato finora, ma imponendo che le velocità passo dopo passo rimangano sempre costanti. L'unico modo per riuscirci è far rimanere costante anche la distanza dal Sole. La Fig. 15 (a sinistra) ci illustra la costruzione eseguita.
Figura 15
Beh... una traiettoria ben nota che aumentando il numero di lati ci porta a una circonferenza di raggio uguale alla distanza costante tra Sole e pianeta. D'altra parte, la nostra traiettoria poligonale ha tutti lati uguali per costruzione. Inoltre, l'angolo SDA è uguale all'angolo DAE (alterni interni di rette parallele per costruzione) e quindi, essendo i triangoli DAE, BAC, ... tutti uguali e isosceli (nuovamente per costruzione) anche l'angolo supplementare di BAC deve rimanere sempre lo stesso per ogni angolo del poligono (tra parentesi questo angolo è anche uguale a quello al centro). Insomma, il poligono che abbiamo costruito ha i lati tutti uguali e anche gli angoli ai vertici, ossia ha i giusti requisiti per essere dichiarato un poligono regolare.
Sì, lo so... si vedeva subito che era un poligono regolare, essendo costruito con otto triangoli isosceli, ma ho voluto usare la via più lunga per definire esattamente un poligono regolare, dato che ci servirà in seguito.
Assodata la traiettoria "regolare", possiamo costruire (Fig. 15, a destra) un altro poligono estremamente importante: a partire dal punto A tracciamo tutte e otto le velocità del primo diagramma ( AC è uguale a DA), e via dicendo... Cosa sono i lati del nuovo ottagono? Ovviamente le differenza tra le velocità, ossia proprio gli spostamento del pianeta verso il Sole ad ogni passo (AM diventa il lato BC). In altre parole, il poligono delle velocità viene costruito con i triangoli azzurri costruiti sui lati del poligono delle distanza dal Sole (quello a sinistra). Anche questo è sicuramente un poligono regolare avendo i lati tutti uguali (le variazioni delle velocità sono uguali per costruzione) e tutti gli angoli supplementari a quelli tra i lati stessi anch'essi uguali dato che sono sempre diretti verso il Sole e sappiamo che l'angolo tra loro rimane costante (è sempre l'angolo al centro dei triangoli isosceli del poligono delle distanze).
Cosa succede, allora, facendo muovere il pianeta a velocità costante lungo la traiettoria di sinistra? Dopo 360° di rotazione si torna al punto di partenza (siamo di fronte a un moto circolare uniforme). Ma la stessa cosa capita anche per la "punta" delle velocità del diagramma di destra che descrive anch'essa una traiettoria che si completa dopo 360°.
E' ora di scrivere qualche semplice formula che descriva sinteticamente e numericamente quanto abbiamo detto a parole.
Possiamo tranquillamente considerare i due diagrammi delle circonferenze (basta aumentare il numero di triangoli isosceli di partenza).
Per il primo a sinistra la variazione dello spazio in un certo tempo dt vale:
v = ds/dt = 2π R/P .... (2) (dove R è la distanza costante Sole - pianeta e P è il periodo orbitale)
Per il secondo a destra la variazione di velocità in un certo tempo dt vale:
dv/dt = 2π v/P .... (3) (dove v è la velocità costante del pianeta e P è lo stesso di prima)
Abbiamo solo scritto che ogni volta che il pianeta compie un'orbita, la sua velocità compie anch'essa una rotazione di 360° nel diagramma delle velocità.
Tuttavia sappiamo che la forza impartita dal Sole vale , utilizzando la (2) e la (3)
F = mdv/dt ∝ dv/dt = 2π v/P = 2π(2π R)/P2 ∝ R/P2 .... (4)
Ma la terza legge di Keplero (dato osservativo!) ci dice che:
P2 ∝ R3 .... (5)
Inserendo la (5 ) nella (4) otteniamo:
F ∝ R/P2 ∝ R/R3 = 1/R2
Ossia, si dimostra che la forza esercitata dal Sole è proporzionale all'inverso del quadrato della distanza del pianeta. Noi l'abbiamo ricavata da un caso particolare, ma la forza è quella che è e non cambia certo cambiando la traiettoria. Ne segue che questa legge è applicabile a tutte le traiettorie per cui vale la seconda legge di Keplero.
Inserto facoltativo: la terza legge di Keplero conoscendo la forza
E' un gioco veramente banale, ma estremamente importante, dato che risolve un punto normalmente raggiungibile con equazioni differenziali. La formula da utilizzare è sempre la (4)
F = mdv/dt ∝ dv/dt = 2π v/P = 2π(2π R)/P2 ∝ R/P2
Ma desso ciò che sappiamo è che la forza è proporzionale all'inverso del quadrato della distanza, ossia:
F ∝ 1/R2
Ne segue che possiamo scrivere:
1/R2 ∝ R/P2
Ossia:
P2 ∝ R3
che è proprio la terza legge di Keplero
Generalizziamo allora il problema, come riportato in Fig. 16, utilizzando molti triangoli per costruire la poligonale, conoscendo, però, la legge della forza che abbiamo ricavata dal caso particolare precedente.
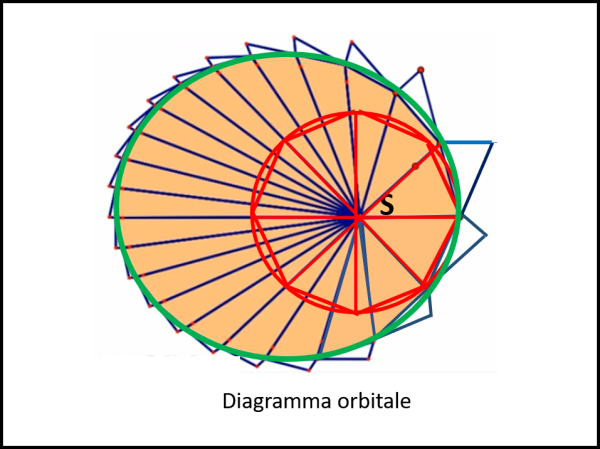
Come si vede bene, è facile a questo punto costruire la curva continua che rappresenta l'orbita del pianeta. Per confronto è stato inserita in rosso anche la traiettoria del caso precedente.
Abbiamo risolto qualcosa. Beh... in realtà non molto, dato che la curva è molto bella ma non sappiamo assolutamente che cosa rappresenta!
Dobbiamo rispondere ancora a due domande:
- La curva delle velocità costruita sulla base delle velocità calcolabili dalla poligonale è un poligono regolare, come nel caso dell'orbita circolare?
- E se per caso lo fosse, come potrebbe dirci che curva la è un'ellisse?
Cominciamo con la prima domanda. E' facile costruire il diagramma delle velocità, in modo analogo a quanto fatto per quello di Fig. 15. Attenzione, però... la figura si basa sulla seconda legge di Keplero, ossia aree uguali in tempi uguali e ne segue che le velocità cambiano da punto a punto. Sì, è vero che possiamo tracciarne quante ne vogliamo, ma il diagramma che otteniamo alla fine, e che ha come lati le variazioni di velocità, non ha assolutamente le caratteristiche di un poligono regolare: i lati sono tutti diversi. Basta disegnare la poligonale delle distanze dal Sole e la relativa poligonale delle velocità per rendersene conto (Fig. 17).
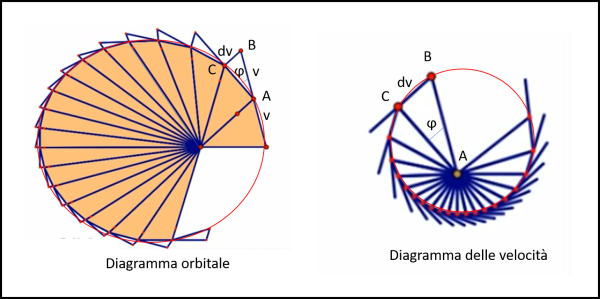
I segmenti relativi alle velocità sono proporzionali ai lati del poligono di sinistra, in quanto la lunghezza dei lati è proporzionale alla velocità, essendo dt una costante (aree uguali in tempi uguali). Potremmo, comunque, considerare anche dt come valore unitario e usare il lato del poligono come valore della velocità.
In parole matematiche:
v = ds/dt con dt costante.
Se dt = 1
v = ds
Notiamo, in particolare, che il triangolo ABC di sinistra si trasferisce pari pari nello stesso triangolo ABC di destra. Essi sono comunque simili (due lati proporzionali e l'angolo compreso φ uguale per costruzione) e scalano a seconda del dt considerato e quindi dell'area spazzata. Come detto, se considerassimo dt = 1, i triangoli di sinistra sarebbero uguali a quelli destra. Nelle figure abbiamo mantenuto il parallelismo tra i segmenti della figura di sinistra e quelli della figura di destra.
Ribadiamo, ancora una volta, che le aree spazzate sono proporzionali all'intervallo di tempo dt considerato. Tempi uguali vogliono infatti dire aree uguali.
dt ∝ A
dove A è l'area spazzata.
Sì, sì... tante belle parole, ma il poligono di destra continua a non essere un poligono regolare!
Dobbiamo proprio affidarci al genio ELEMENTARE di Feynman.