Un numero magico ... ****
Questo quiz è decisamente difficile, lo ammetto. Ma in questo Circolo niente è impossibile... Ovviamente è vietata la ricerca sul web, anche se non è facile trovare la risposta...
La domanda è molto facile: Cosa ha di veramente speciale il numero 495?
Forza, aguzzate l'ingegno e, come regalo, vi prometto un numero ancora più magico, ossia: come la fisica può aiutare la matematica...
28 commenti
Stavolta ci vuole un enigmista....
qui c'è 495 in luogo di 345 (il numero magico pitagorico per la risoluzione del quiz dei tre animaletti... purtroppo non ci ho pensato ...)
C'è un 9 al posto di 3 e inoltre le prime due cifre sono invertite rispetto alla sequenza pitagorica...
E' solo un osservazione non credo sia una traccia per risolvere
no, caro Michele, non c'entra niente....
So che non è una cosa così semplice, caro Enzo, ma mi salta all'occhio che la cifra centrale è la somma delle altre due. Boh sai bene che su questo ho profondi limiti.
caro Mario,
no, ha poca importanza... ma non denigrarti, potresti riuscirci benissimo
... basta avere fantasia e il "guizzo" giusto!
Bho, io ho provato a far girare le 3 cifre e a fare qualche operazione ma l'unica cosa che viene fuori è che 954-459=495. Come dire che la differenza tra le tre cifre ordinate in modo decrescente e crescente mi da quel numero. Ma mi sembra un giochino senza senso (come dire il rapporto tra l'altezza della piramide di Cheope e il lato del campidoglio è 3.14).ci deve essere altro
È anche la differenza fra il numero più grande ottenibile con le cifre 495 e il numero più piccolo.
Se provo con un altro numero, es. 397 , avrò 973-379=594. Guarda caso ottengo ancora le stesse cifre di 495!
Con 783, avrò 873-378= 495 !
Con 813, ottengo 831-138=693 non funziona.
Ma 963-369=594 ,ho ancora le tre cifre.
Come mai?
Quindi Fabio, sembra che abc-cba o da direttamente 495 o da le cifre che rimesse in ordine decrescente e tolto quello crescente alla fine si arriva a 495. Sembrerebbe una certa convergenza a questo numero. Facciamo un po' di prove di verifica.
Quanto trovato da Francesco e Fablop ricorda l' articolo di Enzo sul caos.
Fosse una specie di attrattore?
(100*a+10*b+c)-(100*c+10*b+a)=
99*a-99*c, con a≥b≥c
interessante... e sì, il numero nove ha sempre una grande importanza in molti giochi, come quello del rinoceronte nero in Danimarca... lo conosci?
Ho provato ad esplorare cosa succeda alla serie di numeri con il successore che è la differenza tra il precedente ed il numero ottenuto ribaltandolo. Esempio 942,693,297,-495,99,0.
Partendo da un numero tra -1000 e 1000, i moltissimi casi si passa per +/-495 o +/-594. Il successivo è +/-99 che essendo simmetrico porta la serie a 0.
Un grafico di un campionamento di numeri di partenza comprese tra -1000 e 1000.
Questa figura mi rafforza l'idea che questi numeri possano avere a che fare con gli attrattori.
Partendo da numeri più grandi intorno a +/- 10000 si passa spesso per +/-4995 o +/-5994.
In questo momento non posso andare oltre questo punto.
Ho fatto un po' di prove e ci sono alcune eccezioni:
1. Se le tre cifre sono uguali, non funziona (ovviamente viene zero)
2. Se le tre cifre sono 0 0 1, oppure 0 1 1, non funziona (fa 99 al primo passaggio, e zero al secondo)
Poi la seconda cifra (l'intermedia) è ininfluente: la seconda cifra della differenza abc-cba è in ogni caso 9. Questo dovrebbe ridurre la complessità del problema perché lo abbassiamo allo studio di a e c soltanto.
È ora di smettere di fare prove e di cercare la regola. A più tardi
Partendo da numeri più piccoli si arriva a +-45 o +-54. Tutti numeri che hanno come successore tutti 9:+- 9,99,999
Se scrivo in colonna (l'unico modo che conosco per fare le sottrazioni) ho:
abc -
cba =
xyz
Cioè :
z=c+10-a (essendo c<a)
y=(b-1)+10-b=9 (come mi aspettavo, la cifra intermedia è ininfluente)
x=a-1-c
Ho un sistema di 3 eqz in tre incognite xyz con i tre parametri abc, che si riduce a 2 eqz nelle due incognite xz con i due parametri ac (y è sempre 9 e b è ininfluente).
Se a>c, faccio variare a tra 1 e 9, e c tra 0 e 8 (escludendo il caso 1 0, che darebbe i due casi degeneri 110 e 100). Quanti sistemi mi vengono? Se ho contato bene 39. Dopo continuo
Insomma Fabrizio, abbiamo sempre dentro 4 5 e 9. Io mi ero limitato a ragionare su tre cifre, ma sembra che il gioco si protragga anche oltre. Per ora voglio continuare a ragionare sulle 3 cifre. Sulle due cifre mi sembra che non ci sia un analogo.
bene, bene... vedo che siete scatenati!!!!
100- 001 = 099
990- 099= 891
981-189=792
972-279=693
963-369=594 ci risiamo
Francesco, se considero lo zero in posizione delle centinaia funziona anche con 1 e 11
Ho notato che ad ogni passaggio diminuisce di 1 le centinaia e aumenta di 1 l'unità.
Sì, hai ragione, è che mi fermavo a 3 cifre. Sto preparando una tabella abc e xyz. Avevo escluso tutti i casi che portavano a 99,ma ora li rimetto.
Una cosa che si vede subito è che x+y+z=18. Ci risiamo con multipli di 9
Sì, 495 è il numero che si ottiene sempre prendendo tre qualsiasi cifre (basta che non siano tutte uguali) e facendo la differenza tra i numeri ottenuti mettendole in ordine decrescente, meno quello mettendole in ordine crescente, e rpetendo l'operazione con le tre cifre del risultato. Il numero di passi varia in base alle cifre scelte. È l'ennesimo numero magico (mettiamolo peró dopo il 42 ed il ventordici :wink:)
Un numero di 3 cifre può essere espresso nella forma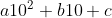
con a,b,c di 1 cifra positiva e a>0.
Il numero trasposto sarà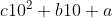
.
La differenza tra i due numeri è un multiplo positivo o negativo di 99.
Con k intero compreso tra 0 e 10,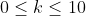
.
Quindi con il primo passaggio otteniamo uno di questi multipli di 99, qualsiasi sia il numero di 3 cifre di partenza. Se il numero di tre cifre è negativo si ottiene lo stesso risultato a segni invertiti.
Volendo vedere come procede successivamente la serie in termini algebrici risulta complesso. Ma avendo ridotto il problema a quello di seguire la sorte di 21 numeri si può fare il forma tabellare/grafica.
Quindi partendo da un numero di 3 cifre positivo o negativo qualsiasi, sottraendogli il suo trasposto otteniamo un numero di questa tabella. Seguendo le frecce otteniamo la prosecuzione della serie.
In tutti i casi il percorso termina sullo 0. Esclusi i casi di entrata nei 99 o nei 594 o di entrata diretta nello 0 (numeri simmetrici), gli altri casi arrivano allo 0 passando per uno dei 495 (positivo o negativo) dopo un percorso più o meno lungo.
Correggo qualche imprecisione nelle considerazioni fatte sopra.
Il risultato della differenza tra un numero di tre cifre ed il suo trasposto è un multiplo positivo o negativo di 99,
Dopo questo primo passaggio entriamo il uno dei numeri di questo diagramma. Seguendo le frecce otteniamo la prosecuzione della serie (ho corretto il diagramma sopra) .
Aggiungo lo stesso diagramma realizzato nella forma che abbiamo visto nell'articolo di Enzo sul caos.
Ciascun punto rappresenta un passo della serie collegando un elemento della serie (ascisse) con il successivo (ordinate). I colori sono quelle del diagramma sopra. La serie che inizia con un qualsiasi numero di 3 cifre termina comunque in un ramo di questo diagramma.
Gli assi sono in parte logaritmici per aiutare la lettura evitando la sovrapposizioni dei punti.
Chissà se tutto questo c'entra qualcosa con la soluzione del quiz?
La soluzione del quiz era molto più semplice...
Lasciamo stare i numeri negativi o differenze che non sono quelle volute... provate a fare lo stesso con un numero a quattro cifre e capiremo che non riusciamo a capire niente...
Mi riallaccio al commento di Fabio di venerdì dove scriveva: 831-138=693
A questo punto se giriamo i numeri in modo da ottenere il numero più grande elo sottraiamo al numero più piccolo otteniamo:
963-369=594
Da cui
954-459=495
"...provate a fare lo stesso con un numero a quattro cifre e capiremo che non riusciamo a capire niente…"
6174?
ho fatto qualche prova a caso. Torna con tutti?
Sembra proprio di sì, caro Francesco, ma potete anche provare con due cifre o con cinque... se ne avete voglia...
Con due cifre ho visto che ovviamente va a zero (due cifre uguali) oppure entra in un loop 9->81->63->27->45->9 che continua a ripetersi (e ci risiamo con la somma a 9)
Con 5 cifre per non starci tutto il giorno dovrei fare un programmino (dovrebbe bastare Excel), ma ora non ho tempo
Insomma, ricapitolando:
prese due cifre a,b qualsiasi (una maggiore dell'altra, a>b) facendo la differenza ab-ba e ripetendo il procedimento, il risultato entra nel loop;
prese tre cifre a,b,c qualsiasi (a>=b>=c, ma a>c) facendo la differenza abc-cba e ripetendo il procedimento, si converge a 495 (che sottoposto al procedimento 954-459 dà sempre 495)
prese quattro cifre a,b,c,d qualsiasi (a>=b>=c>=d, con a>d) e facendo la differenza abcd-dcba e ripetendo il procedimento, si converge a 6174 (che sottoposto al procedimento dà 6174).
Mi ricredo sul numero magico: non è 495, nemmeno 6174 o uno del loop (ce ne sono troppi), ma è il solito 9