Un quiz che riguarda una strana razza di alieni che hanno la poco piacevole mania di portarsi via enormi "carote" di materia dagli altri pianeti. L'unica cosa che rispettano è che ciò che lasciano sul posto deve sempre avere lo stesso volume. Questo quiz è, in qualche modo, legato a quello della corona circolare. Diciamo che è una sua applicazione...

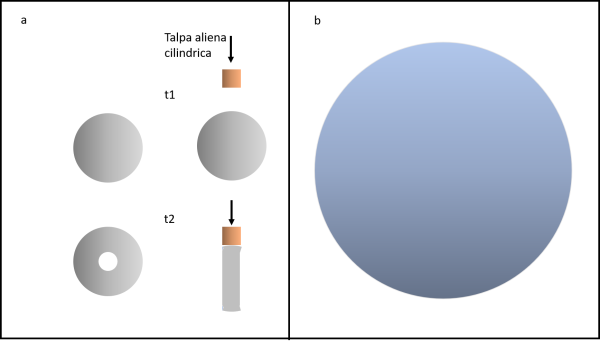
La "talpa" aliena non è altro che un cilindro di raggio variabile capace di estrarre una enorme carota cilindrica da ogni pianeta che incontra. Sfortunatamente, si è imbattuto nel sistema Terra- Luna e ha deciso di agire su entrambi i corpi celesti (non si cura se sono pianeti o satelliti...). Nella Figura che segue vediamo la catastrofica sequela dei fatti...

Nella parte (a) la talpa cilindrica si occupa della Luna. Al tempo t1 si sta avvicinando al bersaglio, mentre al tempo t2 ha già eseguito l'estrazione della carota lunare. A sinistra vediamo la Luna prima dell'operazione (t1) e dopo l'operazione (t2). Della Luna è stato portata via tutta la parte centrale, lasciando solo uno strano anello.

Adesso è il il momento della Terra (parte (b)). Ovviamente, devono cambiare le dimensioni della talpa cilindrica. L'importante è  che la parte che rimarrà della Terra dovrà avere lo stesso volume di ciò che è rimasto della Luna.

Come dovrà essere modificata la talpa affinché si sia sicuri del risultato? E perché ? E quale sarà il valore del volume rimasto, uguale per tutti i pianeti "bucati", in funzione di UNA SOLA variabile?

Non chiedetemi perché gli alieni hanno questa mania omicida... sono o non sono alieni? Tuttavia, una ragione molto assurda c'è, ma ve la spiegherò alla fine...

N.B.: NON VI E' ASSOLUTAMENTE BISOGNO DI USARE INTEGRALI (da cui i due soli asterischi)

P.S.: in qualche modo, questo quiz è strettamente collegato a quello della corona circolare.

Tra uno e l'altro conosceremo qualche teorema e/o principio forse poco noti.