Categorie: Cosmologia Matematica
Tags: elastico formica quiz
Scritto da: Vincenzo Zappalà
Commenti:16
La formica e l'elastico (cosmologico?) ***
Quello che vi propongo è un "apparente" paradosso che ha una soluzione contro intuitiva (a prima vista) e che ha dei risvolti che potrebbero legarlo alla possibilità di ricevere la luce anche da galassie che stanno ben oltre la sfera di Hubble.
Il problema è abbastanza semplice da descrivere:
Abbiamo un elastico che può essere allungato di quanto si voglia. Lo fissiamo a un punto O e mettiamo una formica vicina a tale punto. Poi lasciamo che la formica inizi il suo cammino perfettamente costante, mentre noi allunghiamo l'elastico tirando il suo capo libero in modo continuo, sempre con la stessa velocità. Se io vi dicessi che la velocità della formica è maggiore di quella dell'elastico non avreste alcun dubbio a rispondere alla seguente domanda: "Riuscirà la formica a raggiungere il capo dell'elastico che sto tirando?", "Ovviamente sì!" direste voi... e avreste ragione!
Se, però, allungassi l'elastico a velocità ben maggiore di quella della formica, potrei chiedervi: "Qual è il rapporto limite tra le due velocità tale che la formica riesca a raggiungere la cima dell'elastico?". La soluzione non è banalissima e richiede l'utilizzo di un'equazione differenziale e, quindi, anche di un integrale. Tuttavia, si può anche ottenere il risultato in modo "discreto", tirando l'elastico ogni secondo, permettendo alla formica di camminare ad elastico fermo. La soluzione è piuttosto bella e ci fa conoscere (o richiamare) un qualcosa di molto utile in matematica. Volete provare?
Alla fine, vedremo che si potrà anche sconfinare nel regno della Cosmologia, scegliendo una "formica" molto speciale...
QUI la soluzione
16 commenti
Volevo far presente che questo articolo è stato iniziato sotto forma di QUIZ solo per dare la possibilità di divertirsi un po' ai più esperti in materia. In realtà, potevo presentarlo come argomento completo. Quando sarà data la soluzione essa descriverà i vari tipi di approccio e le ripercussioni sulla stessa cosmologia, Sarà quindi oltremodo interessante per tutti quelli che seguono il nostro Circolo. Quindi, a momento debito, non trascurate di leggere la pseudo- soluzione, dato che essa sarà una trattazione completa di un argomento che trovo piuttosto interessante!
Che ci sia dietro una distanza comovente?
Io la conosco come di trascinamento.
Intendo che la distanza tra formica e arrivo si espande ad un ritmo costante non tanto perchè l'estremo dell'elastico recede ma perchè la strada si "stira" sotto le zampe della formica e trascina pure la formica con sè mentre la formica avanza con la "sua" velocità.
E' proprio quel trascinamento che stabilisce se la formica si avvicina o si allontana dall'arrivo, oppure se prima si avvicina e poi si allontana, o viceversa.
Io conoscevo già la formuletta, perché mi sono trovato a analizzare un'applicazione del problema, non cosmologico ma su una macchina utensile che avendo due punte di taglio, una lavora prima e trascina la seconda che viaggia dietro. Con i controlli numerici e l'elettronica, adesso la fanno facile, ma prima era tutto meccanico, ovviamente non con una formica ed un elastico, ma con ruote dentate, viti senza fine, riduttori, eccetera, che, guardando il moto di avanzamento rettilineo degli utensili producevano lo stesso effetto. E gli alleati, con tale meccanismo, ridussero i tempi di costruzione dei cannoni e dei fucili. Bastava aprire quel paracadute, la mente, come dice il Circolo nella home page.
In pratica, se pensi solo all'elastico, non tutto avanza con la velocità di A: in O deve rimanere fermo. In prima approssimazione puoi pensare che il punto nel mezzo avanza con una velocità metà di v, e così via.
Quindi, la formica all'inizio si sposta con una velocità di trascinamento molto bassa (in zero resterebbe ferma) ma la sua velocità (u) la fa comunque avanzare un pochino di più rispetto al suo punto sull'elastico. Quando comincia ad aver trascorso un po' di spazio, il trascinamento comincia ad aumentare, e a questo si deve aggiungere sempre qualche cosa (u) che per piccolo che sia le fa fare sempre un passo in più sull'elastico, ma trovandosi più avanti di prima il trascinamento aumenta ancora. E così via.
Certo, l'estremità A, a questo punto potrebbe essere scappata via di miliardi di anni luce, ma se nel frattempo la formica ha fatto tanta strada, il trascinamento diventerà sempre maggiore e non si può escludere che una volta superata la metà, la distanza non cominci a diminuire. In fin dei conti, a forza di scavare gallerie le formiche fanno cascare i palazzi (così almeno leggevo nei romanzi da bambino).
Direi che il problema è stato ben puntualizzato. Per dare la risposta definitiva bisogna adesso fare un po' di "conti" o matematici o analitici... Mi raccomando non cercate sul web
secondo me l'elastico deve essere veloce meno del doppio della formica, ma sicuramente avrò sbagliato qualche conto
Bel problema! In tutti due i sensi della frase.
Il risultato che ho ottenuto va contro quello che avrei detto intuitivamente.
La formica presto o tardi, magari molto molto tardi, dovrebbe arrivare all'altro estremo dell'eleastico.
Qualche dubbio sul risultato ottenuto ce l'ho. In particolare sulla separazione tra velocità effettiva della formica e quella dovuta al trascinamente dell'elastico.
Il ragionamento e gli sviluppi algebrici che ho seguito sono questi.
Suppongo che sull'elastico ci siano dei segni equidistanti tarati in modo che segnino 0 al capo dell'elastico da dove parte la formica e 1 al capo opposto. Quando l'elastico viene tirato la distanza tra i segni aumenta, ma rimangono equidistanti e ai due capi segnano sempre 0 e 1. Posso interpretare x come la posizione "relativa" alla lunghezza istantanea dell'elastico.
Ciò che cerco è lo spostamento della formica in termini di x per capire se x riesce ad arrivare a 1.
})
la traduco in termini di velocità per evidenziare il tempo
Lo spostamente istantaneo in termini di x, che chiamo dx, dipende da quanto è allungato l'elastico in quel momento. Lo posso ottenere dallo spostamento "reale", che chiamo dy, dividendolo per la lunghezza attuale dell'elastico.
A questo punto occorre integrare in t il termine a destra per ottenere l'avanzamento x.
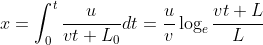
La domanda alla quale rispondere è se x può raggiungere il valore 1 in un tempo finito.
Quindi devo risolvere in t l'espressione di x trovata sopra.
La dipendenza dalla velocità della formica è nel fattore tra parentisi. Per valori di u>0 è finito, magari molto grande, ma finito. Il grafico mostra la dipendenza del fattore dal rapporto u/v.
Vorrei chiarire dovo sono i miei dubbi sul procedimento che ho proposto sopra.
Sostanzialmente sono 2. Ci sto pensando, ma non riesco a risolverli.
E' lecita l'espressione dx=dy/L(t) che assume costante L(t) nell'intervallo di tempo nel quale avviene lo spostamento infinitesimo della formica?
E' lecito assumere dy/dt=u? Forse in dy/dt c'è di mezzo anche v.
caro Fabri, grande come sempre... pensa pure ai tuoi dubbi, ma...la formula finale è OK!!!
Pensa anche al metodo "discreto" che in parte dovrebbe risolvere i tuoi dubbi...
Come complicare la vita ad una povera formichina
Per completare il discorso proseguo con il metodo discreto.
Ho dovuto considerare due effetti contemporanei sulle posizione della formica: il suo moto e l'effetto dell'allungamento dell'elastico. Il moto produce un effetto additivo pari a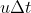
, dove 
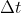è l'intervallo di tempo discreto che stiamo considerando. L'allungamento dell'elastico produce un effetto moltiplicativo pari a }{L(t)})
, dove =v&space;t+L_0)
. I due effetti dovrebbero essere contemporanei, ma nel calcolo ho devuto considerali in sequenza. Se decido di produrre prima l'allungamento e poi il movimento ottengo:
Se faccio la scelta opposta ottengo:
La differenza tra le due è piccola. La prima sottostima leggermente la soluzione analitica, mentre la seconda la sovrastima leggermente.
Quindi partendo da y(0)=0 ed applicando ripetutamente una delle due formule sopra si puo ottenere la posizione della formica nel tempo.
Nelle figure sotto ho messo ciò che ho ottenuto in uno dei casi calcolati.
Ho notato che se il Professore non interviene a breve è perché non è completamente contento delle nostre risposte (di solito perché non abbiamo capito esattamente cosa ci chiedeva, quando sbagliamo, giustamente, ci tira le orecchie). In fin dei conti quanto scritto da Fabrizio va bene, sia nella forma analitica che in quella discreta che approssima benissimo quella analitica.
L'altro giorno in casa guardavamo L'attimo fuggente, e allora provo a salire in piedi sul tavolo per guardare da un'altra prospettiva (ho faticato parecchio perché conoscendo la soluzione analitica, non riuscivo a staccarmi dal ragionamento che avevo già fatto).
Al tempo 0, F sta in zero e A sta nella lunghezza iniziale, ma il Prof. nel problema non aveva parlato della lunghezza iniziale e ci chiedeva il rapporto tra u e v per vedere se la formica raggiunge l'arrivo: quindi ho dovuto pensare senza lunghezza iniziale e ho provato soltanto con gli avanzamenti.
Chiamo aF l'avanzamento della formica sull'elastico, e aA l'avanzamento dell'arrivo.
Dopo 1 secondo
aF = u
aA = v
Dopo 2 secondi
aF = u
aA=v+v=2v
Dopo 3 secondi
aF = u
aA= 2v+v=2v
...
Dopo i secondi
aF=u
aA=(i-1)v+v=iv
Dopo varie prove ho ceduto al ragionamento che avevo già fatto per la soluzione analitica e ho inserito i rapporti degli avanzamenti accanto a questi avanzamenti (forse è un imbroglio, forse sono sceso dal tavolo)
dopo 1 secondo rapporto aF/aA=u/v
dopo 2 secondi rapporto aF/aA=u/2v
dopo 3 secondi rapporto aF/aA=u/3v
…
dopo i secondi rapporto aF/aA=u/iv
Quindi la formica raggiungerà l'arrivo quando la somma di tutti i rapporti sarà uguale a 1
u/v+u/2v+u/3v+...+u/iv=1
Se raccolgo u/v ottengo
u/v*(1+1/2+1/3+...+1/i)=1
cioè
u/v*sommatoria (per i che va da 1 a qualcosa) di (1/i)
Non me la ricordavo ed ho fatto una ricerca: quella sommatoria è detta serie armonica, che è sempre positiva, sempre crescente e per i che tende ad infinito diverge anche lei ad infinito (in realtà wikipedia dice che "per un i sufficientemente grande , la somma parziale dei termini da 1 a i può superare qualunque numero prefissato"). Quindi vuol dire che prima o poi, dopo i secondi, la formica raggiunge l'arrivo.
La Formica raggiunge A (sicuro che prima o poi lo fa), per qualsiasi rapporto tra u e v, quando la sommatoria (1/i) diviene v/u (probabilmente a questo punto dovrò aggiungere anche la lunghezza iniziale dell'elastico, che la formica deve in ogni caso superare).
Così mi piaci Francesco!!! Aspettavo proprio che facesse il suo ingresso la serie armonica
Leggendo in rete sulla serie armonica, ho trovato che i greci ne erano veramente appassionati, e cercavano di metterla ovunque (magari anche nell'ouzo).